| 基于改进传统人工势场法的机器人避障和路径规划研究 |
移动机器人技术发展至今, 路径规划和避障策略一直是国内外学者研究的重点和难点[3]。移动机器人在实际工作中周围信息未知的程度可以分为信息完全已知环境, 半未知环境和完全未知环境。对于第一类情况, 我们可以使用全局的路径规划来实现最优路径的选择。目前较为流行的全局路径规划的算法有遗传算法, 快速随机搜索树算法, 人工蜂群算法等[4]。但是生活中工作的机器人大部分是处于第二或者第三类的情况, 比如在室内环境中的柜子和墙脚这些不可移动的障碍物, 还有桌椅和房门等可随时移动的障碍物。
未知环境中的避障问题属于局部路径规划, 这种避障方法比全局路径规划更加实用, 相当于是机器人边走边看边规划, 主要影响避障效率的是传感器测得环境的精确度和机器人使用的避障算法。局部路径规划主要有人工势场法, 神经网络方法, 遗传算法, 蚁群算法和模糊逻辑控制算法等[5]。
本文选择了人工势场法进行研究和改进, 是因为人工势场法起步较早, 研究的成果较多, 算法较为成熟, 且相交于其他的算法, 人工势场法的算法较为简单, 规划出来的路径比较平滑且安全。
但是在相对复杂的环境信息中, 障碍物和目标点形成的特殊位置关系会使人工势场法暴露出很多的问题。例如在几个障碍物十分靠近时机器人将很难找到的路径; 在一个狭窄的通道, 机器人会来回摆动:目标点附近存在障碍物时, 机器人将很难找到目标点[6]。
许多学者通过各种方法的研究来克服传统人工势场法存在的问题。王奇志通过限定障碍物范围的方法来解决人工势场法中存在的局部极小值的问题; Matoui等将独立的机器人组成一个网络, 使机器人之间可以进行信息交互, 降低了机器人碰撞障碍物的几率, 提高了机器人的安全性[7]; Zhang提出势场法结合混沌算法的新方法, 针对势场法中存在的机器人在某些特定路径上反复摇摆的缺陷提出了新的解决方案[8]。
传统的人工势场法无法适应目前日益多变的工作环境, 且存在局部极小值的问题, 针对这些问题, 本文提出了一种通过改变传统斥力函数的方法来解决局部极小值的问题。改进后的斥力函数保证了目标点为全局势场的最低点, 从而保证机器人能够顺利到达目标点。最后进行算法仿真, 仿真结果表明改进后的算法能有效克服局部极小值问题, 使机器人安全有效地完成路径规划。
1 传统人工势场法人工势场法最早由Khatib在1986年提出, 是从物理学中衍生出来的一种思想[9]。该方法首先应用在防止机械手臂在一同抓取物体时碰到工作台。假设机械臂在虚拟立场中运动, 目标点的周围存在虚拟的引力, 障碍物周围存在虚拟的排斥力, 两者的合力作为机械臂的动力。人工势场法是运用物理学的认识论来描述人类思维的方法[10]。后来研究者们发现, 该方法在移动机器人应用中有很好的效果, 产生的运动轨迹十分平滑。
机器人在执行任务的环境中存在障碍物时, 认为在障碍物周围存在斥力场, 在目标点周围存在引力场, 机器人向着势函数下降的方向来实现无碰撞地到达目标点。斥力场的方向在障碍物指向机器人的连线上, 引力场的方向在机器人指向目标点的连线上。势函数是一个以距离为变量的函数, 设引力函数为
引力场函数一般如下式:
| $ {{\vec E}_{att}}(p) = {k_{att}}{\left( {p - {p_{goal}}} \right)^m} $ | (1) |
式中pgoal表示目标点的位置(xg, yg); p表示机器人的空间位置(x, y); katt表示引力常数量; m表示可调参数量; p-pgoal是机器人和目标点之间的欧几里德距离。对引力势函数对距离求导得到其梯度即引力:
| $ {{\vec F}_{att}}(p) = - \nabla {{\vec E}_{att}}(p) $ | (2) |
类似地有斥力势函数一般形式如下式:
| $ {{\vec E}_{rep}}(p) = \left\{ \begin{array}{l} {k_{rep}}{\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right)^n},p - {p_{obs}} < {d_0}\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,p - {p_{obs}} \ge {d_0} \end{array} \right. $ | (3) |
式中pobs表示障碍点的空间位置(xobs, yobs); krep表示斥力场常量; d0表示障碍物影响半径; n表示可调参数; p-pobs表示机器人和障碍点之间的欧几里德距离。对斥力函数对距离求导得到其梯度即斥力:
| $ {{\vec F}_{rep}}(p) = - \nabla {{\vec E}_{att}}(p) $ | (4) |
总的势场函数表示为:
| $ {{\vec E}_{total}}(p) = {{\vec E}_{att}}(p) + \sum\nolimits_i {{{\vec E}_{rep}}(p)} $ | (5) |
机器人在空间p所受的合力(如图 1所示)为:
| $ {{\vec F}_{total}}(p) = - \nabla {{\vec E}_{total}} = {{\vec F}_{att}}(p) + \sum\nolimits_i {{{\vec F}_{rep}}(p)} $ | (6) |
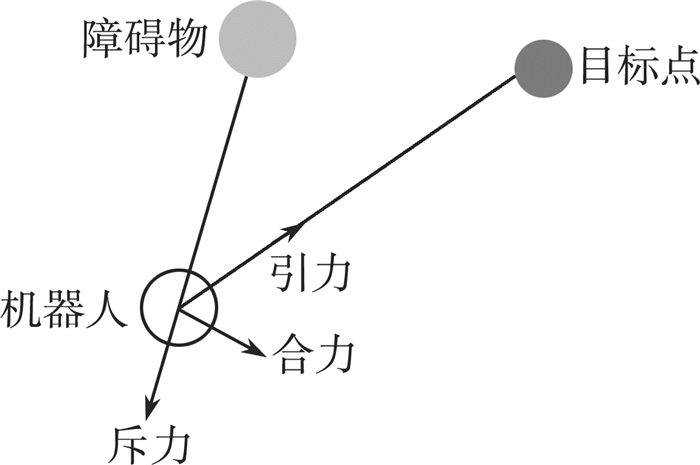 |
| 图 1 机器人在势场中的受力情况 |
机器人离目标点越远, 目标点对其产生的吸引力就越大, 引力势能越大:反之, 当机器人和目标点的距离为零时, 吸引势就随之消失, 机器人向目标点靠近的过程就是引力势场逐渐下降的过程[11]。
与目标点不同, 这些障碍为机器人创造了一种排斥力, 机器人越接近障碍, 它的排斥力就越大, 排斥势能就越大, 排斥力就越大; 反之, 机器人离障碍物越远, 产生的排斥力就越小, 当机器人离障碍物一定距离时, 障碍物对其的排斥力就为零。
但是在相对复杂的环境信息中, 障碍物和目标点形成的特殊位置关系会使人工势场法暴露出很多的问题。例如在几个障碍物十分靠近时机器人将很难找到的路径; 在一个狭窄的通道, 机器人会来回摆动; 目标点附近的障碍存在时, 机器人将很难找到目标点。如果在目标点附近存在障碍物, 且机器人仍处于障碍物的排斥作用范围内, 当机器人行驶近障碍物附近时, 障碍物就会对其产生斥力, 靠得越近产生的斥力就越大, 目标点对机器人产生的引力相对于斥力来说则相对较小, 这就会导致机器人往离目标点远的方向前进, 前进一段距离后就又向着目标点移动, 以此循环往复, 从而出现机器人不能抵达目标点的现象[12]。
2 改进人工势场法 2.1 局部极小值在实际的工作环境中, 由于障碍物的数量很多, 机器人的受力情况十分复杂。当机器人行进到起始点和目标点的中间某一点时, 目标点对机器人的引力和障碍物对目标点的排斥力是完全相等和相反的, 此时机器人受到的合外力为零[13]。此时机器人就会误以为自己到达了目的地而停止运动或者在该点附近徘徊, 不知道下一步的运动方向, 从而出现机器人不能到达目标点的现象成为局部极小值现象。这个现象是传统的人工势场法中存在的最大的缺点和不足, 为此许多的科研人员都致力于解决这个问题来提高人工势场法的适用范围:王志奇通过限定障碍物范围的方法来解决极小值的问题Matoui等将独立的机器人组成一个网络, 使机器人之间可以进行信息交互, 降低了机器人碰撞障碍物的几率, 提高了机器人的安全性; Zhang提出势场法结合混沌算法的新方法, 针对势场法中存在的机器人在某些特定路径上反复摇摆的缺陷提出了新的解决方案。
2.2 解决局部极小值为了克服传统势场法中出现的局部极小值以至于无法到达目标点的缺陷, 本文的方法是基于对斥力势函数的改进[14]。当移动机器人驶向目标点时, 所受的斥力将减少, 改进后的斥力函数如:
| $ {{\vec E}_{rep}}(p) = \left\{ \begin{array}{l} \frac{1}{2}{k_{rep}}\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right)^2{\left( {p - {p_{goal}}} \right)^n},\\ p - {p_{obs}} < {d_0}\\ 0,p - {p_{obs}} \ge {d_0} \end{array} \right. $ | (7) |
其中p-pobs是一个矢量, 表示机器人和目标点之间的欧几里德距离, 方向在机器人指向目标点的连线上。该式子与传统的斥力势函数相比, 多了一个(p-pgoal)n, 这个式子的作用是保证机器人在达到目标点时的势场值是机器人运动过程中最小的, 这就解决了势场法中出现的机器人无法到达目标点的问题。
当p≠pobs时, 此时机器人并未到达目标点, 求斥力场函数的梯度得到斥力表达式:
| $ \begin{array}{l} {{\vec F}_{rep}}(p) = - \nabla {{\vec E}_{rep}}(p) = \left\{ \begin{array}{l} {k_{rep}}\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right)\\ 0 \end{array} \right.\\ \left\{ {\begin{array}{*{20}{c}} {\frac{{{{\left( {p - {p_{goal}}} \right)}^n}}}{{{{\left( {p - {p_{goal}}} \right)}^2}}} + \frac{n}{2}{k_{rep}}{{\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right)}^2}}\\ 0 \end{array}} \right.\\ \left\{ {\begin{array}{*{20}{c}} {\left( {p - {p_{goal}}} \right)n - 1}\\ 0 \end{array}} \right. \end{array} $ | (8) |
| $ 令:{{\vec F}_1} = {k_{rep}}\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right)\frac{{{{\left( {p - {p_{goal}}} \right)}^n}}}{{{{\left( {p - {p_{goal}}} \right)}^2}}} $ | (9) |
| $ \begin{array}{l} {{\vec F}_2} = \frac{n}{2}{k_{rep}}{\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right)^2} \cdot \\ \;\;\;\;\;\;\;{\left( {p - {p_{goal}}} \right)^{n - 1}} \end{array} $ | (10) |
对式(9)和(10)进行讨论分析:
(1) 当0<n<1时:
| $ \begin{array}{l} \mathop {\lim }\limits_{p - {p_{goal \to 0}}} {{\vec F}_1} = \mathop {\lim }\limits_{p - {p_{goal \to 0}}} \left[ {{k_{rep}}\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right) \cdot } \right.\\ \left. {\frac{{{{\left( {p - {p_{goal}}} \right)}^n}}}{{{{\left( {p - {p_{goal}}} \right)}^2}}}} \right] = 0 \end{array} $ | (11) |
| $ \begin{array}{l} \mathop {\lim }\limits_{p - {p_{goal \to 0}}} {{\vec F}_2} = \mathop {\lim }\limits_{p - {p_{goal \to 0}}} \left[ {{k_{rep}}\frac{n}{2}\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right) \cdot } \right.\\ \left. {{{\left( {p - {p_{goal}}} \right)}^{n - 1}}} \right] = 0 \end{array} $ | (12) |
当机器人靠近目标点使, 障碍物对机器人的斥力
(2) 当n=1时:
| $ \begin{array}{l} \mathop {\lim }\limits_{p - {p_{goal \to 0}}} {{\vec F}_1} = \mathop {\lim }\limits_{p - {p_{goal \to 0}}} \left[ {{k_{rep}}\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right) \cdot } \right.\\ \left. {\frac{{{{\left( {p - {p_{goal}}} \right)}^n}}}{{{{\left( {p - {p_{goal}}} \right)}^2}}}} \right] = \infty \end{array} $ | (13) |
| $ \begin{array}{l} \mathop {\lim }\limits_{p - {p_{goal \to 0}}} {{\vec F}_2} = \mathop {\lim }\limits_{p - {p_{goal \to 0}}} \left[ {\frac{n}{2}{k_{rep}}\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right) \cdot } \right.\\ \left. {{{\left( {p - {p_{goal}}} \right)}^{n - 1}}} \right] = \frac{n}{2}{k_{rep}}{\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right)^2} \end{array} $ | (14) |
当机器人靠近目标点时, 障碍物对机器人的斥力
(3) 当>1时:
| $ \begin{array}{l} \mathop {\lim }\limits_{p - {p_{goal \to 0}}} {{\vec F}_1} = \mathop {\lim }\limits_{p - {p_{goal \to 0}}} \left[ {{k_{rep}}\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right) \cdot } \right.\\ \left. {\frac{{{{\left( {p - {p_{goal}}} \right)}^n}}}{{{{\left( {p - {p_{goal}}} \right)}^2}}}} \right] = 0 \end{array} $ | (15) |
| $ \begin{array}{l} \mathop {\lim }\limits_{p - {p_{goal \to 0}}} {{\vec F}_2} = \mathop {\lim }\limits_{p - {p_{goal \to 0}}} \left[ {{k_{rep}}\frac{n}{2}\left( {\frac{1}{{p - {p_{obs}}}} - \frac{1}{{{d_0}}}} \right) \cdot } \right.\\ \left. {{{\left( {^p - {p_{goal}}} \right)}^{n - 1}}} \right] = 0 \end{array} $ | (16) |
当机器人靠近目标点时, 障碍物对机器人的斥力
本文利用Matlab软件针对传统的人工势场法的局部极小值的问题和该进后的人工势场法进行了仿真, 以下仿真结果均是在静态障碍物的前提下进行的。仿真结果表明, 改进后的人工势场法具有更强的环境适应性, 避障更加稳定安全, 达到了预期的避障效果。
仿真过程采用10*10的环境地图, 共设置了7个障碍物, 以(0, 0)为起始点, (10, 10)为目标点, 以横向为x轴, 纵向为y轴, 障碍物的坐标分别为(2, 2), (3, 3), (3, 6), (4, 5), (5, 6)(9.5, 9.5), 机器人的步长设定为0.2。改进前后势场法仿真对比图如图 2所示。
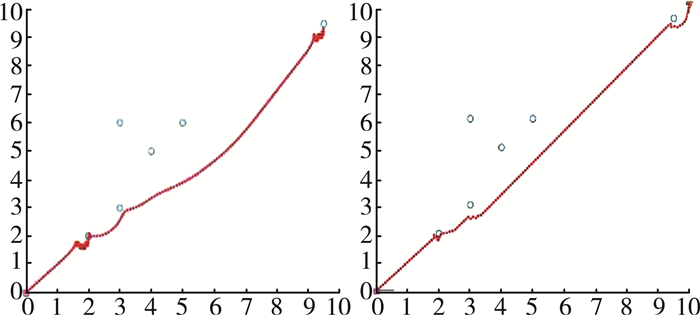 |
| 图 2 改进前后势场法仿真对比图 |
通过图 2的仿真结果可以看出, 当移动机器人陷入局部极小值时, 未改进算法前的机器人会误以为到达了目标点而会在某一范围内不断来回移动, 无法靠近目标点; 改进后的算法由于障碍物对机器人的斥力变小, 而标点给机器人的引力大于斥力, 机器人会绕开障碍物继续向目标点移动最终顺利到达目标点。
| 表 1 传统势场法与改进势场法数据对比 |
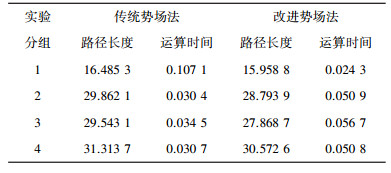 |
上表是传统势场法和改进后势场法的仿真数据对比。通过表格可以直观的看出改进后的势场法的路径长度相较于传统的势场法有了明显的改善。但是, 改善后的算法对于传统的算法规划路径的时间需要在以后的研究中投入更多的关注。
局部极小值是人工势场中难以解决的问题之一, 本文针对这个问题提出了解决策略, 将传统的斥力函数进行改进, 确保了目标点是全场势能最低点, 避免机器人在局部极小值处停滞或者徘徊, 保证机器人顺利到达目标点。
除此之外, 本次仿真实验的过程中, 还将改进后的势场法和其他优秀的路径规划的算法进行纵向比较, 比较各种算法之间的优缺点, 为后续的研究做铺垫。
图 3是改进后的人工势场法和A*算法的对比图, 通过对比我们可以清晰的看出改进后的势场法规划出来的路径比A*算法规划的路径更加的平滑而且安全, 相反A*算法仿真出来的路径锯齿较多, 路径较长, 且易与障碍物相碰撞。
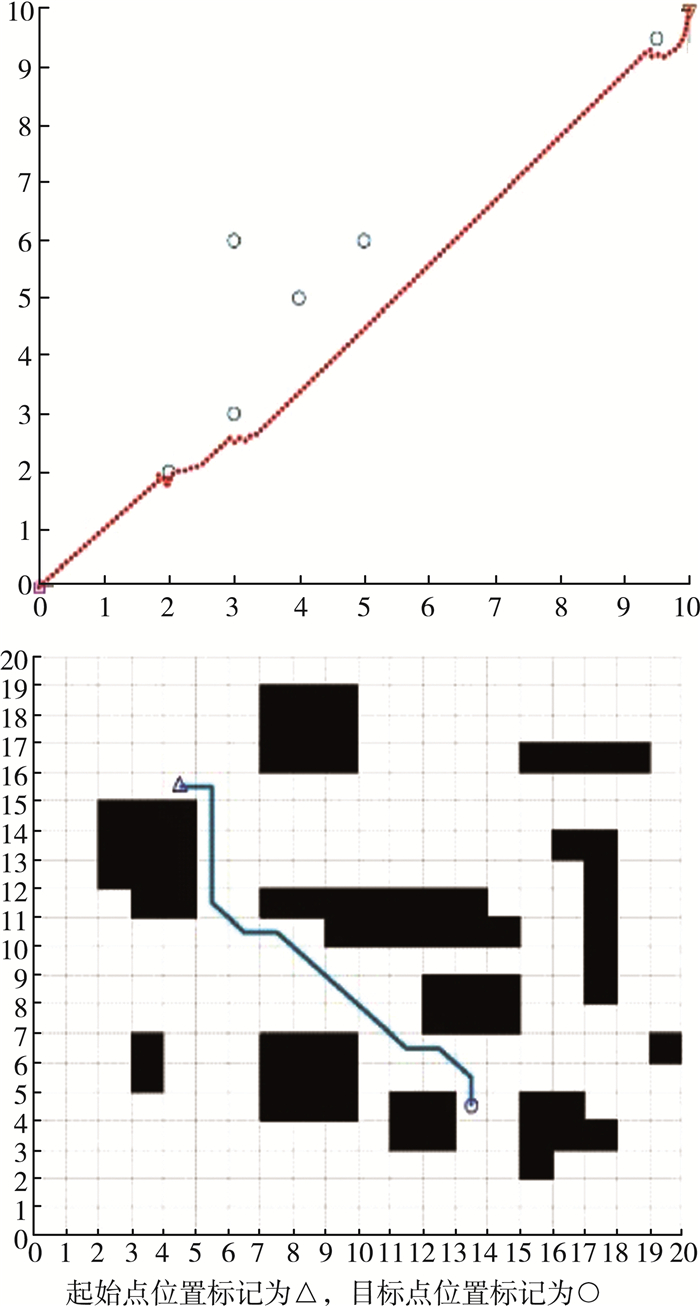 |
| 图 3 人工势场法和A*算法的仿真对比 |
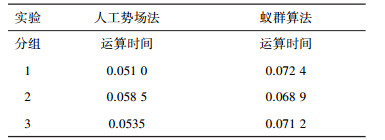
下表是相同的路径长度下人工势场法和蚁群算法的运算时间的数据对比, 通过表格可以直观的看出人工势场法在相同的路径的长度下规划的时间明显要少于蚁群算法, 这是由于蚁群算法本身的算法导致的。算法的复杂性导致了运算时间的变长。
| 表 2 势场法与蚁群算法运算时间对比 |
 |
通过改进算法与原算法的仿真比较, 势场法与目前其他优秀算法的比较, 都可以使我们更好的了解各个算法的优缺点, 为以后的更加深入的研究提供更好的便利。
| [1] |
王攀攀.部分未知环境中移动机器人动态避障研究[D].哈尔滨: 哈尔滨工业大学, 2012.
|
| [2] |
徐飞. 基于改进人工势场法的机器人避障及路径规划研究[J]. 计算机科学, 2016, 43(12): 293-296. DOI:10.11896/j.issn.1002-137X.2016.12.054 |
| [3] |
郜辉, 吕志刚. 人工势场法目标不可达的研究[J]. 国外电子测量技术, 2018, 37(01): 29-33. |
| [4] |
韩伟, 孙凯彪. 基于模糊人工势场法的智能全向车路径规划[J]. 计算机工程与应用, 2018, 54(06): 105-109. |
| [5] |
温素芳, 郭光耀. 基于改进人工势场法的移动机器人路径规划[J]. 计算机工程与设计, 2015, 36(10): 2818-2822. |
| [6] |
AMIR NASRINAHAR, JOOM HUANG CHUAH. Intelligent motion planning of a mobile robot with dynamic obstacle avoidance[J]. Journal on Vehicle Routing Algorithms, 2018, 1(2-4): 89-104. DOI:10.1007/s41604-018-0007-4 |
| [7] |
Yi ZHU, TAO ZHANG, JINGYAN SONG, et al. A new method for mobile robots to avoid collision with moving obstacle[J]. Artificial Life and Robotics, 2012(4): 507-510. |
| [8] |
刘欢, 王健, 李金凤, 等. 未知环境下机器人避障设计研究[J]. 机械设计与制造, 2013(10): 236-238. DOI:10.3969/j.issn.1001-3997.2013.10.074 |
| [9] |
吴登峰, 梅志千, 尹力伟, 等. 一种未知环境下室内移动机器人路径规划新算法[J]. 机电工程, 2015, 32(03): 389-392. |
| [10] |
李凡.移动机器人视觉定位与避障系统研究[D].成都: 西南石油大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10615-1016098678.htm
|
| [11] |
XUN CHAI, FENG GAO, CHENKUN QI, et al. Obstacle avoidance for a hexapod robot in unknown environment[J]. Science China Technological Sciences, 2017, 60(6): 818-831. DOI:10.1007/s11431-016-9017-6 |
| [12] |
顾幸方, 陈晋音. 移动机器人未知环境避障研究[J]. 传感器与微系统, 2011, 30(05): 16-20. DOI:10.3969/j.issn.1000-9787.2011.05.005 |
| [13] |
SCHACHT-RODRIGUEZ R., PONSART J.-C., GARCIA-BELERAN C.-D., et al. Path planning generation algorithm for a class of UAV multirotor based on state of health of lithium polymer battery[J]. Journal of Intelligent & Robotic Systems, 2018, 91(1): 115-131. |
| [14] |
DOOSITE S., HOSHIA A.K., NAZARAHARI M., et al. Optimal path planning of multiple nanoparticles in continuous environment using a novel adaptive[J]. Genetic Algorithm, 2018, 3(2): 208-215. |
 2019, Vol. 33
2019, Vol. 33


