| 基于PSO的ELM集成学习算法研究 |
单隐层前向神经网络具有简单的网络结构和良好的全局逼近能力, 在机器学习领域得到广泛的应用。但是由于大多数学习算法是基于梯度下降进行寻优, 所以存在收敛速度慢和容易陷入局部极小点等缺点[1]。
为了克服传统神经网络的缺点, Huang等人[2]提出了一种全新的单隐层前馈神经网络, 即极限学习机(Extreme Learning Machine, ELM)。该神经网络通过随机生成网络的输入权值和隐层偏差, 减少了过多的人工干预, 通过最小二乘法求解输出层权值, 从而完成对网络的训练。网络能以极快的学习速度达到较好的泛化性能, 解决了传统神经网络学习速度缓慢的缺点, 拓宽了神经网络的应用范围, 在函数逼近、模式识别和人脸识别等领域得到较为广泛的应用。
由于ELM学习算法的参数是随机设定的, 因此网络性能稳定性相对不高。针对这一问题, 很多学者相继提出了优化ELM参数的方法, 使得网络整体趋向于稳定并提高网络的泛化性能。例如, 在文献[3]中, Xu等人提出了PSO-ELM学习算法; 在文献[4]中, Han等人利用惯性权值自适应调整的IPSO-ELM算法来优化ELM算法的参数; 在文献[5]中, Zhu等人利用差分进化算法来调整ELM的输入层和隐层连接权值和偏差, 提高了ELM算法的性能; 在文献[6]中, 提出了一种RELM算法, 在ELM算法中引入了正则化参数C; 文献[7]在RELM的基础上, 提出了结合加权最小二乘法的WRELM算法; 在文献[8]中, 提出了IRW-ELM算法, 可以自适应地根据训练数据的不同赋予不同的权值。在文献[9]中, 采用参数自适应粒子群优化策略来调整神经网络中的输入权值和隐层偏差; 同时, 一些研究者提出应用集成学习[10]的思路来提高ELM算法的学习性能。文献[11]提出将集成学习和交叉验证嵌入到训练阶段的EN-ELM算法; 文献[12]提出一种V-ELM的算法, 通过训练大量差异性的基分类器并把它们的结果通过多数投票进行集成, 表现出了优于单个ELM的性能; 文献[13]将GA与ELM相结合, 提出GA-ELM集成算法; 文献[14]提出一种叫作V-QELM的算法, 该算法通过结合ELM和q-Gaussian激活函数, 并在不同的基分类器中赋予q不同的值来达到差异化的目的; 文献[15]将Bagging与ELM相结合, 提出Bagging-ELM算法; 文献[16]提出了选择性集成的思路; 文献[17]通过加权投票的思想给予每个基分类器一定的权重, 并根据权重的大小来进行集成; 文献[18]提出基于差分进化的极限学习机加权集成方法; 文献[19]提出了一种基于差分进化的选择性集成学习算法来解决分类问题。
为了更好地提高ELM算法的性能, 在PSO-ELM的基础上, 基于PSO优化ELM的参数, 选取前M个最优个体, 分别求出其输入权值和偏差, 然后求出输出权值。函数逼近问题中, 基于实际输出与期望输出之间的误差, 取其平均值作为最后的评价标准; 模式分类是在集成的基础上, 采用最大投票原则来提高模型的泛化性能, 相应的算法称为E-PSO-ELM学习算法。文献[18]、[19]中提出利用差分进化算法(Differential Evolution, DE)集成来提高ELM的分类能力, 称为E-DE-ELM学习算法。为了更好地比较智能优化算法PSO和DE的性能, 利用E-PSO-ELM算法的思想, 将E-DE-ELM算法扩展到函数逼近问题的求解。
1 极限学习机极限学习机算法结构图如下:
如图 1所示, 有N个样本{(xi, ti)}i=1N, 隐含层具有Ñ个节点, 激活函数为G(·)的ELM学习算法的数学模型为:
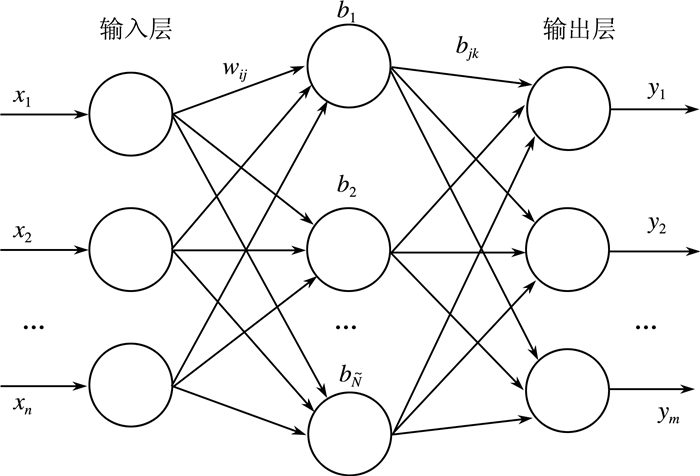 |
| 图 1 极限学习机结构图 |
| $ \begin{array}{*{20}{c}} {{f_{\tilde N}}\left( x \right) = \sum\limits_{i = 1} {{\beta _i}G\left( {{w_i},{b_i},x} \right)} }&{x \in {R^n},{w_i} \in {R^n}} \end{array} $ | (1) |
其中:Ñ为隐层节点的个数; wi是连接第i个隐层节点和输入节点的连接权; bi是第i个隐层节点的偏差; βi是连接第i个隐层节点和输出节点的权值; G(wi, bi, x)表示第i个隐层节点的输出。
具有Ñ(Ñ < N)个隐层神经元的ELM学习算法能够以零误差逼近N个离散的样本值。公式(1)可以写成矩阵的形式:
| $ H\beta = T $ | (2) |
其中:H是隐层输出矩阵[20], β是隐层和输出层间的输出权值, T是期望输出。
| $ H = {\left[ {\begin{array}{*{20}{c}} {G\left( {{w_1},{b_1},{x_1}} \right)}& \cdots &{G\left( {{w_{\tilde N}},{b_{\tilde N}},{x_1}} \right)}\\ \vdots&\cdots&\vdots \\ {G\left( {{w_1},{b_1},{x_N}} \right)}& \cdots &{G\left( {{w_{\tilde N}},{b_{\tilde N}},{x_N}} \right)} \end{array}} \right]_{N \times \tilde N}} $ |
| $ \beta = {\left[ {\begin{array}{*{20}{c}} {b_1^T}\\ \vdots \\ {b_{\tilde N}^T} \end{array}} \right]_{\tilde N \times m}},T = {\left[ {\begin{array}{*{20}{c}} {t_1^T}\\ \vdots \\ {t_N^T} \end{array}} \right]_{N \times m}} $ |
正如在文献[21]、[22]、[23]中所分析的, 通过随机设定隐层节点的参数, 相对应的隐层输出矩阵H就被唯一确定。由公式(2)可以求出输出权值β, 即β=H+T, H+是矩阵H的Moore-Penrose广义逆。
极限学习机(ELM)总结如下:
给定训练样本数据集{(xi, ti)}i=1N, 隐层节点个数Ñ, 激活函数G(·):
1) 随机初始化输入权值wi和偏差bi, i=1, …, N;
2) 计算隐层输出矩阵H;
3) 计算输出权值β:β=H+T。
2 粒子群优化算法1995年, Kennedy和Eberhart[24]提出了粒子群优化(Particle Swarm Optimization, PSO)算法。该算法和遗传算法类似, 属于一种基于种群的、启发式优化算法。与遗传算法相比, PSO算法概念简明、容易实现、具有较快的收敛速度, 在科学研究和工程应用领域都得到了较为广泛的应用。
PSO算法与其他启发式优化算法一样, 首先初始化一个种群, 其个数为m, 然后将种群中的每个个体看作N维搜索空间中的一个没有体积的微粒, 每个微粒在搜索空间中以一定的速度飞行, 其飞行速度根据自身的飞行经验及其周围其他微粒的飞行经验进行动态调整。
设在N维空间内, 由m个粒子组成初始种群:P=(x1, x2, …, xi, …, xm)T; 粒子i的位置信息:xi=(xi1, xi2, …, xiN)T, i=1, 2, …, m; 粒子i的速度:vi=(vi1, vi2, …, viN)T, i=1, 2, …, m。
计算m个粒子的适应值。找到当前的最优解, 然后根据公式(3)和(4)来更新:
| $ \begin{array}{l} v_i^{t + 1} = wv_i^t + {c_1} * rand\left( \; \right) * \left( {P_i^t - x_i^t} \right)\\ \;\;\;\;\;\;\;\;\;\; + {c_2} * rand\left( \; \right) * g\left( {P_g^t - x_g^t} \right) \end{array} $ | (3) |
| $ x_i^{t + 1} = x_i^t + v_i^{t + 1} $ | (4) |
其中, i:一个种群中的第i个粒子; t:当前迭代次数; vit:粒子i在第t次迭代中粒子的速度; xit粒子i在第t次迭代中粒子的位置; c1、c2:学习因子, 具有调节Pi和Pg的相对重要性的功能; 函数rand():在0~1区间上产生一个随机数; w:惯性权重, 其值是非负的(若w的值较大, 则全局寻优能力强, 局部寻优能力弱; 若w的值较小, 则全局寻优能力弱, 局部寻优能力强)。动态惯性权重能获得比固定值更好的寻优结果。
在PSO初始化参数的过程中, 为了保证算法在迭代初期具有较高的探索能力, 在迭代后期加快算法的收敛速度, 可将w设为随着迭代次数线性减小, 其表示形式为[9]:
| $ \begin{array}{l} w\left( t \right) = {w_{{\rm{Max}}}} - Iteration \times \left[ {\left( {{w_{{\rm{Max}}}} - {w_{{\rm{Min}}}}} \right)/\left( {Max\_} \right.} \right.\\ \left. {\left. {iteration} \right)} \right] \end{array} $ | (5) |
其中, wMax和wMin分别表示惯性权重在迭代过程中的最大值和最小值。Iteration表示当前迭代次数, Max_iteration表示最大迭代次数。
另外, 为了提高算法迭代后期的收敛速度, 采用具有时变特性的加速度系数[25], 在算法的初始迭代阶段, 较大的c1和较小的c2可以保证微粒在整个搜索空间的运动特性; 在算法的最后迭代阶段, 较小的c1和较大的c2可以保证微粒收敛于问题的全局最优解。c1和c2动态调整公式表示为:
| $ {c_2} = \frac{{2 \times {{\left( {{\rm{Iteration}}} \right)}^3}}}{{{{\left( {{\rm{Max\_iteration}}} \right)}^3}}} $ | (6) |
| $ {c_1} = \frac{{\left( { - 2} \right) \times {{\left( {{\rm{Iteration}}} \right)}^3}}}{{{{\left( {{\rm{Max\_iteration}}} \right)}^3} + 2}} $ | (7) |
在集成算法中, 将ELM的输入权值和隐层偏差作为粒子群优化算法中的参数, 将ELM学习样本期望输出与实际输出的均方根误差(RMSE)作为PSO的适应值, 根据每个粒子的适应值, 应用公式(3)和(4)来更新粒子的位置和速度。当达到算法的最大迭代次数后, 取当前种群的前M个最优个体, 然后将这M个最优个体重新带入到网络中训练, 最后求出这M个最优个体的实际输出, 然后求出与期望输出之间的平均误差。
3.2 函数逼近问题集成使用粒子群优化算法优化ELM的参数, 输出最后一次迭代的粒子, 根据每个粒子的适应值进行升序排列, 选取前M个粒子进行训练, 得到各自对应的w和b, 求出相应的实际输出Y。取M个粒子实际输出的平均值, 再求出与期望输出之间的误差。计算公式如下:
| $ {\rm{error}} = \sqrt {\frac{{\sum\limits_{i = 1}^M {{{\left( {T - \sum\limits_{i = 1}^M Y } \right)}^2}} }}{M}} $ | (8) |
如3.2所述, 选取前M个最优个体进行训练, 通过这M个独立神经网络, 可以得到M组分类结果, 标记分类正确的结果为1, 分类错误的结果为0, 然后采用最大投票原则, 对相同样本的分类结果进行投票, 票数多者作为最终的分类结果。最后统计正确分类样本的个数, 计算分类正确率。公式如下:
| $ {\rm{accuracy}}\;{\rm{rate}} = \frac{{\sum\limits_{i = 1}^N {{n_{1i\left( {\max \left( {\sum\limits_{r = 1}^M {{n_{0r}}} ,\sum\limits_{r = 1}^M {{n_{1r}}} } \right)} \right)}}} }}{N} $ | (9) |
其中:N为样本总数, n1为分类正确的样本, n0为分类错误的样本, M为集成神经网络个数。max():若样本分类正确数大于样本分类错误数, 则输出1, 反之, 输出0;
从而集成算法(E-PSO-ELM)总结如下:
设定隐层节点个数为Ñ, 迭代次数为K, 神经网络集成的数目为M, 种群个数为P。
训练阶段:
1) 初始化种群, 随机产生P组初始输入权值和偏差, 作为PSO算法的第一代粒子。
2) k=1, 2, …, K
(ⅰ)确定适值函数并计算每个粒子的适值, 求出每个粒子的个体极值和全局极值;
(ⅱ)更新粒子的速度和位置;
(ⅲ)k=k+1。
3) 结束。
4) 得到最优的ELM参数值, 根据适应值进行升序排序。选择前M个进行集成。
集成阶段:
r=1, …, M
(ⅰ)将M个最优个体重新带入网络, 计算输出权值, 最终计算得到实际输出Y;
(ⅱ)r=r+1;
(ⅲ)结束。
函数逼近:
1)
2) 再根据公式(8)求得误差。
模式分类:
1) 判定分类是否正确;
2) 根据公式(9)计算分类正确率。
4 仿真实验实验平台如下:中央处理器(CPU)为IntelICoreIi5-4570K 3.20 GHz, 内存(RAM)容量为4.00 GB, 编程环境为Matlab2016a。
在实验中, M的取值为10。在仿真分析中, 函数逼近和模式分类各选3个数据集。数据集的参数信息如表 1所示, 括号中为数据集样本数。为了使实验结果更有说服力, 最终的实验结果为10次实验结果的平均值。
| 表 1 计算机仿真数据集 |
 |
PSO-ELM[9]和E-PSO-ELM的初始参数设置如表 2所示, DE-ELM[5]和E-DE-ELM[18-19]的初始参数设置如表 3所示。
| 表 2 PSO算法参数 |
 |
| 表 3 DE算法参数 |
 |
图 2和图 3分别表示在Box and Jenkins数据集下函数逼近问题和在Diabetes数据集下模式分类问题的测试误差随着隐层神经元个数增加的变化曲线, 从图形中可以看出, 网络的复杂程度对测试误差具有较大的影响。所以, 在处理不同的问题时, 针对不同的数据集, 要恰当地选择合适的隐层神经元个数, 以提高网络的泛化能力。
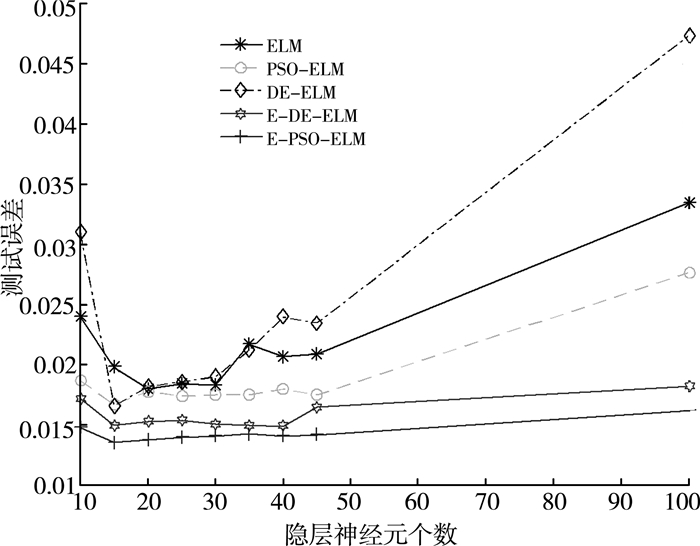 |
| 图 2 Box and Jenkins数据集下, 测试误差与隐层神经元个数关系图 |
 |
| 图 3 Diabetes数据集下, 测试误差与隐层神经元个数关系图 |
对于Box and Jenkins数据集, 实验采用隐层神经元个数为15的网络结构, 而对于Mackey Glass和Autompg数据集, 采用隐层神经元个数为35的网络结构。对于模式分类问题, 由于Iris和Wine数据集较小, 所以设置隐层神经元个数为15, 而Diabetes数据集较大, 所以设置隐层神经元个数为35。
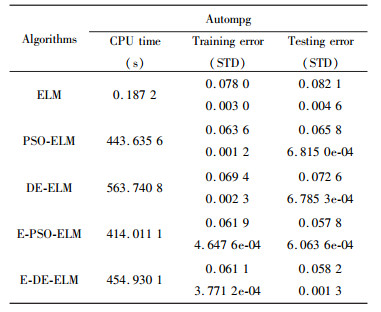
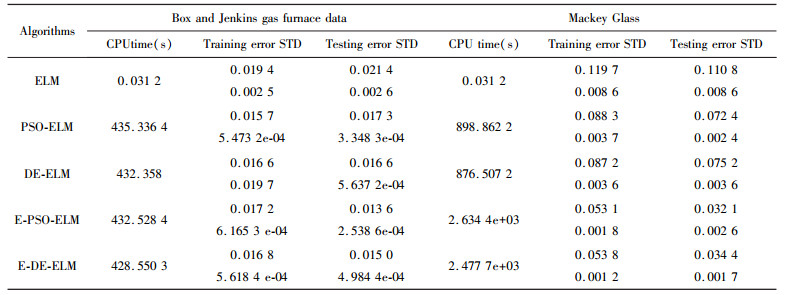
表 4为在Autompg数据集下, 函数逼近的实验结果; 表 5为在Box and Jenkins和Mackey Glass数据集下, 函数逼近的实验结果; 表 6为在Wine和Iris数据集下, 模式分类的实验结果。由于Wine和Iris数据集较小, 所以实验增加一个较大的Diabetes数据集, 分别设置样本个数为500和250, 迭代次数为100和50, 进行仿真实验。由表 5可以看出:用PSO和DE改进的ELM算法, 在函数逼近方面测试精度得到较大的提高; 在PSO-ELM和DE-ELM的基础上, 增加了集成方法, 所得到的测试精度比PSO和DE的测试精度更高。说明所提出方法可以较好地提高函数逼近问题的性能。
| 表 4 Autompg数据集下, 函数逼近仿真结果 |
 |
| 表 5 Box and Jenkins gas furnace data和Mackey Glass数据集下, 函数逼近仿真结果 |
 |
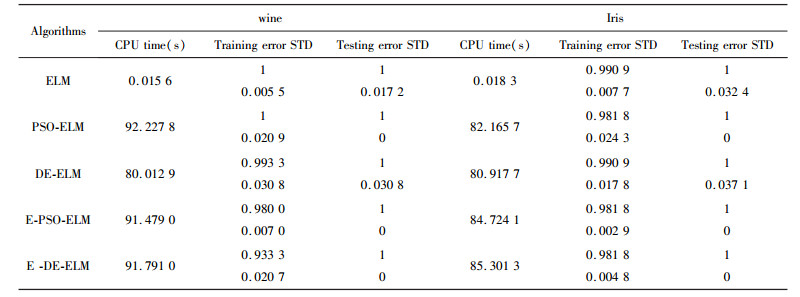
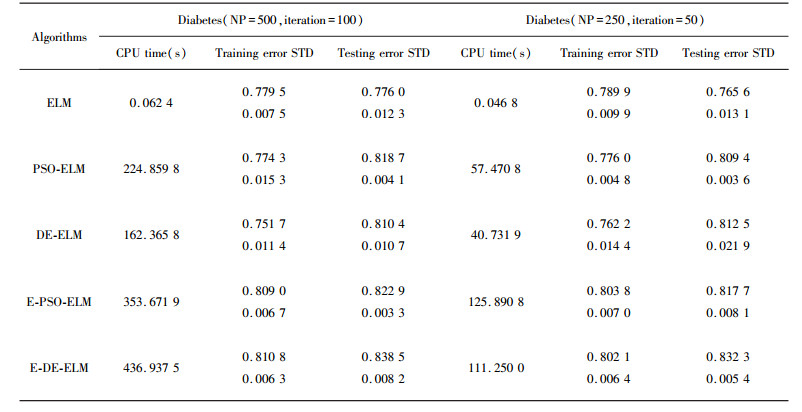
模式分类问题中, 由表 6可知:采用最大投票原则改进的PSO-ELM和DE-ELM与原始的PSO-ELM、DE-ELM和ELM在分类的精度上相差无几, 都有很高的测试精度。由表 7可知:E-PSO-ELM的精度比PSO-ELM的精度较高, 虽然与E-PSO-ELM相比, 性能略有降低, 但亦可说明所提出的E-PSO-ELM具有较好的性能。
| 表 6 Wine和Iris数据集下, 模式分类仿真结果 |
 |
| 表 7 Diabetes数据集下, 模式分类仿真结果 |
 |
5 结语
为了提高ELM学习算法的泛化能力, 在PSO-ELM的基础上加入集成部分, 提出了E-PSO-ELM学习算法。函数逼近和模式分类问题的仿真结果表明, 所提出算法具有较好的性能, 特别是在函数逼近问题中, 可以较为明显地提高模型的泛化能力和学习精度。
| [1] |
LI J, SU M Y.Extreme learning machine with multiple kernels in Proc[C].IEEE International Conference on Control and Automation, 2013.
|
| [2] |
HUANG G B, WANG D H, LAN Y. Extreme learning machines:a survey[J]. International Journal of Machine Learning and Cybernetics, 2011, 2(2): 107-122. DOI:10.1007/s13042-011-0019-y |
| [3] |
XU Y, YANG S. Evolutionary extreme learning machine-based on particle swarm optimization[J]. Springer Berlin Heidelberg, 2006, 36(3): 644-652. |
| [4] |
HAN F, YAO H F, LING Q H.An improved extreme learning machine based on particle swarm optimization[C].ICIC, 2011: 699-704.
|
| [5] |
ZHU Q Y, QIN A K, SUGANTHAN P N, et al. Evolutionary extreme learning machine[J]. Pattern Recognition, 2005, 38(10): 1759-1763. DOI:10.1016/j.patcog.2005.03.028 |
| [6] |
HUANG G B, ZHOU H M, DING X J et al.Extreme learning machine for regression and multiclass classification[C].IEEE Transactions on Systems, Man, and Cybemetics, Part B: Cybemetics, 2012.
|
| [7] |
DENG W Y, ZHEN Q H, CHEN Z L.Regularized extreme learning machine[C].IEEE Symposium on Computational Intelligence and Data Mining, 2009.
|
| [8] |
HORATA P, CHIEWCHANWATTANA S, SUNA K. Robu stextreme learning machine[J]. Neurocomputing, 2013(102): 31-44. |
| [9] |
李彬, 李贻斌, 刘猛.基于参数自适应调整粒子群优化策略的极端学习机[C].青岛: 第27届中国控制与决策会议, 2015.
|
| [10] |
HANSEN L, SALARNON P. Neuralnetwork ensembles[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(10): 993-1001. DOI:10.1109/34.58871 |
| [11] |
LIU N, WANG H. Ensemble based extreme learning machine[J]. IEEE Signal Processing Letters, 2010, 17(8): 754-757. DOI:10.1109/LSP.2010.2053356 |
| [12] |
LIU N, CAO J W, LIN Z P, et al. Evolutionary voting-based extreme learning machine[J]. Information Sciences, 2012, 185(1): 66-77. DOI:10.1016/j.ins.2011.09.015 |
| [13] |
XUE X, YAO M, WU Z, et al. Genetic ensemble of extreme learning machine[J]. Neurocomputing, 2014, 129(10): 175-184. |
| [14] |
STOSIC D, STOSIC D, LUDERMIR T. Voting based q-generalized extreme learning machine[J]. Neurocomputing, 2016(174): 1021-1030. |
| [15] |
SAMAT A, DU P, LIU P, et al. Ensemble extreme learning machines for hyperspectral image classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(4): 1060-1069. DOI:10.1109/JSTARS.4609443 |
| [16] |
ZHOU Z H, WU J X, TANG W. Ensembling neural networks:many could be better than all[J]. Artificial Intelligence, 2002, 137(1): 239-263. |
| [17] |
LI K, KONG X, LU Z, et al. Boosting weighted ELM for imbalanced learning[J]. Neurocomputing, 2014, 128(5): 15-21. |
| [18] |
海宇娇, 刘青昆. 基于差分进化的ELM加权集成分类[J]. 计算机工程与应用, 2017, 53(8): 57-60. |
| [19] |
ZHANG Y, LIU B, YANG F.Differential evolution based selective ensemble of extreme learning machine[C].Trustcom/bigdatase/ispa.IEEE, 2017.
|
| [20] |
HUANG G B. Learning capability and storage capacity of two-hidden layer feedforward networks[J]. IEEE Transactions on Neural Networks, 2003, 14(2): 274-281. DOI:10.1109/TNN.2003.809401 |
| [21] |
HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine:a new learning scheme of feedforward neural networks[J]. IEEE International Joint Conference on Neural Networks, 2005(2): 985-990. |
| [22] |
HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70(1): 489-501. |
| [23] |
HUANG G B, ZHU Q Y, SIEW C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE Transactions Neural Networks, 2006, 17(4): 879-892. DOI:10.1109/TNN.2006.875977 |
| [24] |
KENNEDY J, EBERHART R C.Particle swarm optimization[C].In: Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth: IEEE: Piscataway, 1995: 1942-1948.
|
| [25] |
RATNAWEERA A.C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 240-243. DOI:10.1109/TEVC.2004.826071 |
 2018, Vol. 32
2018, Vol. 32


