| “希望特性”串联校正方法及仿真研究 |
在现代工业体系中, 自动控制技术的应用愈加的广泛。自动控制系统有时存在性能指标不能满足设计要求的问题, 因此需要加入一些装置或者机构进行校正[1]。校正方法基本上就是超前校正、迟后校正、迟后超前校正三种。然而这三种方法都需要在特定的系统参数下才可以使用, 有局限性, 因此我们使用“希望特性”的校正方法进行系统校正。在使用校正环节之后, 系统的超调量和调节时间减小, 系统的响应速度加快, 稳定性和快速性得到了很好的改善[2]。
1 “希望特性”校正方法的含义常规的校正设计方法是L0(ω)+LC(ω)=L(ω) (L0(ω)是原系统的频率特性, LC(ω)是校正装置的频率特性, L(ω)是设计完成系统的频率特性), 而“希望特性”校正的方法就是将要求的性能指标转化为对数幅频特性, 再与原系统的频率进行比较, 得到校正装置的参数和形式, 设计方法为L(ω)-L0(ω)=LC(ω)。
2 系统校正装置的设计 2.1 校正前系统的分析设定单位反馈系统的开环传递函数为
| $ {G_0}\left( S \right) = \frac{K}{{S\left( {\frac{S}{{10}} + 1} \right)\left( {\frac{S}{{50}} + 1} \right)\left( {\frac{S}{{100}} + 1} \right)\left( {\frac{S}{{200}} + 1} \right)}}, $ | (1) |
要求系统满足r(t)=t→
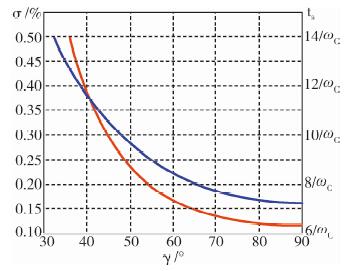 |
| 图 1 时域-频域转换图 |
通过建立G0(S)的传递函数MATLAB的指令如下:
>> g1=tf(1, [1 0]);
>> g2=tf(1, [1/10 1]);
>> g3=tf(1, [1/50 1]);
>> g4=tf(1, [1/100 1]);
>> g5=tf(1, [1/200 1]);
>>GS=200*g1*g2*g3*g4;
绘制其校正前开环传递函数的BODE图, 并得到截止频率和相角裕度, 指令如下:
>> margin(GS)
>> [GM0, PM0, WCG0, WCP0]=margin(GS)
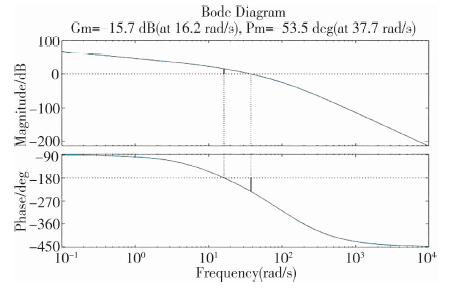 |
| 图 2 校正前系统的BODE图 |
由命令行窗口得到的结果可知相角裕度γ0≈-53.5°, 系统校正前是不稳定的, 为此就需要通过“希望特性”校正的方法来找到校正装置的参数。
2.2 校正装置的设计 2.2.1 校正前后系统幅相曲线的绘制1) 在
2) 在ω2=0.1
3) 在ω4=130处做-100dB/dec直线(与L0(ω)高频段同斜率);
图 3中的曲线1为系统校正前的幅频曲线, 曲线2为系统校正后的幅频曲线。
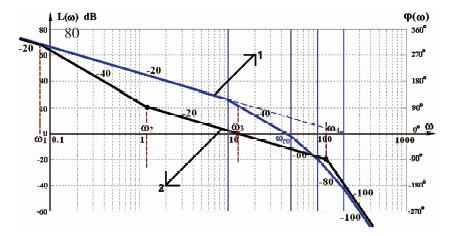 |
| 图 3 校正前及校正后的幅频曲线 |
2.2.2 校正装置的幅频曲线
利用L(ω)-L0(ω)=LC(ω), 图 3中曲线2的斜率减去图 3中曲线1的斜率得到曲线3的斜率。
在ω≤ω1的频率范围, 校正装置的斜率为-20dB/dec-(-20dB/dec)=0dB/dec。
在ω1≤ω≤ω2的频率范围, 校正装置的斜率为-40dB/dec-(-20dB/dec)=-20dB/dec。
在ω2≤ω≤10的频率范围, 校正装置的斜率为-20dB/dec-(-20dB/dec)=0dB/dec。
在10≤ω≤50的频率范围, 校正装置的斜率为-20dB/dec-(-40dB/dec)=20dB/dec。
在50≤ω≤100的频率范围, 校正装置的斜率为-20dB/dec-(-60dB/dec)=40dB/dec。
在100≤ω≤130的频率范围, 校正装置的斜率为-20dB/dec-(-80dB/dec)=60dB/dec。
在130≤ω≤200的频率范围, 校正装置的斜率-40dB/dec-(-20dB/dec)=-20dB/dec。
在200≤ω的频率范围, 校正装置的斜率为-100dB/dec-(-100dB/dec)=0dB/dec。
由此得到校正装置的幅频曲线, 如图 4中的曲线3所示。
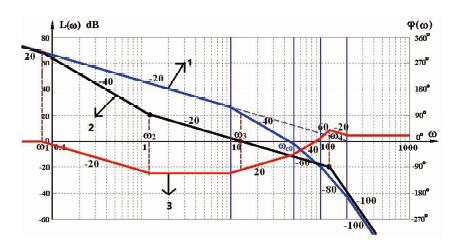 |
| 图 4 校正装置的幅频曲线 |
但是由于中频—高频交界处太复杂, 我们可以在不影响系统性能的前提下进行简化[4]。图 4中曲线3中频率在ω3≤ω的部分斜率全部变成-20dB/dec, 与0分贝线交于ω4。简化后校正装置的幅频曲线如图 5中的曲线3所示。
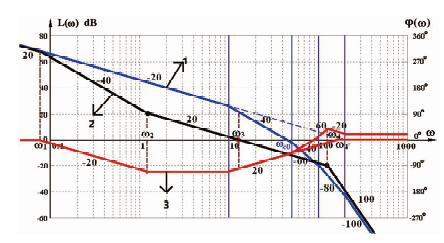 |
| 图 5 中-高频简化后校正装置的幅频曲线 |
2.2.3 确定校正装置的传递函数
根据下列程序, 计算校正装置的传递函数:
>> g1=tf(1, [1 0]);
g2=tf(1, [1/10 1]);
g3=tf(1, [1/50 1]);
g4=tf(1, [1/100 1]);
g5=tf(1, [1/200 1]);
GS=200*g1*g2*g3*g4*g5;
margin(GS);
[GM0, PM0, WCG0, WCP0]=margin(GS);
WC=13;W2=WC/10;
W4=WCP0^2/WC;
W1=10*W2/W4;
m1=tf([1/W2 1], 1);
m2=tf([1/10 1], 1);
m3=tf(1, [1/W1 1]);
m4=tf(1, [1/W4 1]);
Gc=m1*m2*m3*m4;%校正装置的传递函数
zpk(Gc)
运行后得到的结果:
| $ {\rm{Gc}} = \frac{{{\rm{(s + 1)(s + 1}}.3{\rm{)}}}}{{{\rm{(s + 109}}{\rm{.2)(s + 0}}{\rm{.119)}}}} $ | (2) |
Continuous-time zero/pole/gain model.
2.2.4 系统BODE图验证利用上面设计的校正装置校正后得到的系统BODE如图 6所示, 经过校正后系统的相角裕度γ≈44.1°, 远远好于未进行校正系统的相角裕度, 满足设计的要求[5]。
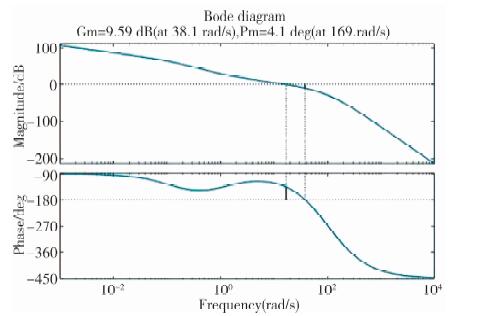 |
| 图 6 校正后系统的BODE图 |
3 结论
本次设计了基于MATLAB的系统“希望特性”串联校正, 该方法简单、快捷, 可以在较少的条件下设计出满足系统性能要求的校正装置。结合使用MATLAB进行相关的计算, 可以减少计算量和计算所出现的错误, 提高效率, 可以在以后的工程广泛的应用[6]。
| [1] |
杨风霞. 一种基于零极点对消法的串联校正环节[J]. 信息记录材料, 2019, 20(04): 154-155. |
| [2] |
於沈刚, 马明舟, 岳雪峰, 等. 模糊PID智能灌溉控制器的设计及MATLAB仿真[J]. 节水灌溉, 2018, 273(05): 92-95. |
| [3] |
王帆, 张永安, 阳胜, 等. 基于Matlab仿真算法的光源空间相干性研究[J]. 激光与光电子学进展, 2017(09): 350-357. |
| [4] |
宋建国, 许灵, 牟蓬涛. 基于Matlab 12/8极开关磁阻电机控制系统仿真[J]. 电力电子技术, 2017, 51(2): 75-77, 80. |
| [5] |
李文宇, 王延军, 高飞, 等. 滞后系统的一种改进PID控制方法[J]. 自动化与仪器仪表, 2017(1): 19-21. |
| [6] |
孙萍. 电力推进船舶控制系统的设计与校正[J]. 电子技术与软件工程, 2019(11): 139. |
 2020, Vol. 34
2020, Vol. 34

