| 基于半张量积的立体车库网络调度算法 |
2. 齐鲁工业大学 人事处,济南 250353;
3. 山东栋梁科技设备有限公司,济南 250022
2. Human Resources office, Qilu University of Technology, Jian 250353, China;
3. Shandong Dongliang Technology Equipment Co. Ltd, Jinan 250022, China
在城市发展的同时,居民的生活和消费的理念发生了很大的变化,城市中汽车的数量不断增加。随之而来的,就是如何城市有限的空间停放不断增加的汽车的问题。如果不能合理的设计车位,不仅无法停放更多的汽车,甚至还会引发交通不畅等问题。立体车库就是一个能有效解决此类问题的新方案。而要将立体车库有效的发挥其功能,就必须要有一个高效率的调度算法来实现[1]。而常见的部分采用升降横移的三维式立体车库,路径规划方式都太过简单和死板,不适用于大型立体车库的路径规划和后期维护工作。
现有的立体车库设计一般较为简单,不能充分利用空间,依然有较大的升级潜力。例如纵向式立体车库,仅仅将一个车位在纵向进行了拓展,这种车库无法做到很高的层次。而一些普通的三维立体车库运行缓慢,无法将层数做高。若层数太高,由于运行速度限制和算法优化不到位等原因,则会有很长的等待时间。使用嵌入式设计、PLC(Programmable Logic Controller)工业控制、半张量积网络查询调度算法实现立体车库的设计。存取车时可更快的到达目标车位,节省等待时间。介绍了一种半张量积的立体车库网络查询调度算法,实现了在不同规格的立体车库产品中智能化地计算出最佳路径,有效地解决了目前算法存在的问题,降低了生产成本,提高了立体车库可维护性[2-4]。
1 半张量积理论在计算机存储中,并不是将数据排列成二维形式来实现矩阵运算,使用的是“指针”和其衍生结构等来表示。在运用中,这种使用方法的效率高于二位形式的排列方法,其原因在于指针可以有层次的使用,这种用法不只能够排列数据为矩阵结构,还能构造数据排列为三维乃至多位的结构。通过研究希望发现一项新的方法,并且用其来完成此类高层次的数据的运算。在这种情况下,引入了左半张量积概念[5-6]。常用的矩阵乘法的计算过程促使引入一种新的矩阵乘法,定义如下:
定义1.1 设T是一个np维行向量,X是一个p维列向量。将T分割成p个等长的块,他们都是n维行向量。定义左半张量积
| $ T\ltimes X=\sum\limits_{i=1}^{p}{{{T}^{i}}{{x}^{i}}\in {{R}^{n}}}。$ | (1) |
我们利用这种新乘法,给出一个可行的算法。
定义1.2
1) 设X={x1, …xs}是一个行向量,Y={y1, …ys}T是一个列向量。
情形1:如果t是s的因子,即s=t×n,则n维行向量
| $ {\left\langle {X, Y} \right\rangle _L}: = \sum\limits_{k = 1}^t {{X^k}yk} \in {R^n}, $ | (2) |
称为X和Y的左半张量积,这里
| $ X = \left[{{X^1} \cdots, {X^T}} \right], {X^i} \in {R^n}, i = 1, \cdots, t。$ | (3) |
情形2:如果s是t的因子,即t=s×n,则n为列向量
| $ {\left\langle {X, Y} \right\rangle _L} = {\left( {{{\left\langle {{X^T}, {Y^T}} \right\rangle }_L}} \right)^T} \in {R^n}, $ | (4) |
也称为X和Y的左半张量积[7]。
2) 设M∈Mm×n, N∈Mp×q如果n是p的因子或者p是n的因子,称C=M×N是M和N的左半张量积,如果C由m×n个块组成,即C=(Cij),并且
| $ {C^{ij}} = {\left\langle {{M^i}, {N_j}} \right\rangle _L}, i = 1, \cdots m, j = 1, \cdots, q。$ | (5) |
3) 设A∈Rm×n, B∈Rp×q, 那么A和B的半张量积为
| $ AB = \left( {A \otimes {I_{\frac{a}{n}}}} \right)\left( {B \otimes {I_{\frac{a}{P}}}} \right), $ | (6) |
其中α=lcm(n, p)是n和p的最小公倍数,
注:定义1.2中的第1) 条中,如果t=s,则左半张量积就变成标准内积。因而在定义1.2的第2) 条中,如果n=p,则矩阵的左半张量积就退化成普通矩阵乘法。因此说左半张量积是普通矩阵乘法的推广。
给定两个矩阵Mm×n和Np×q,有定义当且仅当下列情况之一成立:
1) 如果n%p=0,则此时乘积M
2) 如果p%n=0,则此时乘积M
注:为方便计,当n=p是,我们称M, N满足等维数条件,当n%p=0或p%n=0是我们成M, N满足倍维数条件。半张量积就是将矩阵乘法从满足等维数条件的矩阵推广到倍维数条件的矩阵对。
3) 我们将定义两个具有任意维数的矩阵的左(右)半张量积,但它仅限于该节,其余部分我们仅对满足维数条件的矩阵对定义矩阵的左(右)半张量积。
定理1.1 设f{x1, …xn}为一个逻辑函数, 在向量形式下f:Δ2n→Δ。则存在唯一逻辑矩阵Mf∈L2×2n,称为f的结构矩阵, 使得f(x1, …, xn)=Mf
| $ x = \ltimes ^{i}_{n} = 1{x_1}。$ |
考虑常用逻辑算子及其结构矩阵, 用到的算子结构矩阵为:
| $ \begin{align} &M_\wedge ={{\delta }_{2}}\left[1\text{ }2\text{ }2\text{ }2 \right], M_\vee ={{\delta }_{2}}\left[\text{1 1 1 2} \right], \\ &{{M}_{\oplus }}={{\delta }_{2}}\left[2\text{ 1 1 }2 \right]。\\ \end{align} $ | (7) |
注:在n=p时的情况下,矩阵A与B的半张量积便是正常的矩阵乘法运算。因此我们认为,半张量积可以看作正常矩阵乘法运算的延伸,并且,正常矩阵乘法运算的部分性质在半张量积的运算中依然可用。中提到的矩阵乘法运算都看作是半张量积, 所以在不引起混淆的前提下,将半张量积运算符号“
与现有技术相比,所述立体车库的优点和积极效果如图 1所示,所述立体车库的车位为4×5×10立体式,车位分为地上五层和地下五层,纵向预留9个车位空间,横向预留4个车位空间作为存取车通道:共有188个可用车位。第六层取车时无需立体车库动作,可直接取车;留出一列只放置一个车位,需要调度时将该车位调整至预留列第六层,则该车位可存取车辆。使用多排式立体车库,相比单排式立体车库,每增加一排即能多存放一列车位;相比两层无避让立体车库,能放置更多的车位,可最大限度地利用可配置空间。
 |
| 图 1 立体车库结构图 |
3 立体车库存取车过程规划
所述立体车库设计的车位数量增加的同时,也为车位的取出指定车位与寻找空余车位提出了更高的要求。所述的基于半张量积的立体车库采用的网络查询算法,将立体车库的状态存储在多维数组,其中还包含各状态的连接信息,这些信息通过左半张量积运算来验证,运算过程都进行了量化[9]。通过以下算法求出最优路线:
第1步,构造三维数组S={aijk|i, j=1, …, m; k=1, …n},其中i,j表示立体车库中的车位状态;m为车位状态总数;k表示立体车库网络中的存取车路径;n为存取车路径总数。当路径k经过车位状态i,j时,aijk=dijk;当路径k不经过车位状态i,j时,aijk=0,其中dijk表示存取车路径k上,车位状态i,j间的距离,同时需要注意,当i=j时aijk:=0。
将数组S分别按照索引
| $ S_{ij}^k = \left[\begin{array}{l} {a_{111}} \cdots {a_{1m1}}\;\;{a_{211}} \cdots {a_{2m1}}\;\; \cdots \;\;{a_{m11}} \cdots {a_{mn1}}\\ {a_{112}} \cdots {a_{1m2}}\;\;{a_{212}} \cdots {a_{2m2}}\;\; \cdots \;\;{a_{m12}}d{a_{mn2}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {a_{11n}} \cdots {a_{1mn}}\;\;{a_{2mn}} \cdots {a_{2m1}}\;\; \cdots \;\;{a_{m1n}} \cdots {a_{mnn}} \end{array} \right],$ | (8) |
| $ S_{ji}^k = \left[\begin{array}{l} {a_{111}} \cdots {a_{1m1}}\;\;{a_{211}} \cdots {a_{2m1}}\;\; \cdots \;\;{a_{m11}} \cdots {a_{mn1}}\\ {a_{112}} \cdots {a_{1m2}}\;\;{a_{212}} \cdots {a_{2m2}}\;\; \cdots \;\;{a_{m12}} \cdots {a_{mn2}}\\ \;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {a_{11n}} \cdots {a_{1mn}}\;\;{a_{2mn}} \cdots {a_{2m1}}\;\; \cdots \;\;{a_{m1n}}L \cdots {a_{mnn}} \end{array} \right]。$ | (9) |
第2步,对于起始车位状态i和目的地车位状态j,判断两车位状态是否可以直达。首先,构造检验向量aij=Sijk·ei·ej,其中ep表示第p个坐标为1的m维单位列向量,依据半张量积运算性质,可得aij=(aij1, …, aijn)T表示车位状态i,j的连接信息,构造检验数bij=Sijk·aij若bij>0,说明车位状态i和车位状态j之间存在直达路径。接着查询最短路径,若min{ aijk| aijk >0, k=1, …, n}=aijk’,此时通过存取车路径k’,可实现车位状态i,j间的连接,也就是说车位只需要从起始车位状态i通过编号为k′的路径就可直达目的地车位状态j,并且路径k′是起讫车位状态间距离最短的直达路径,此时起讫车位状态i,j间运行距离为d=aijk’。
第3步,若不存在连接起讫车位状态的直达存取车路径,就需要考虑一次状态转换路线。首先,构造直达矩阵
| $ A_{j}=S_{ij}^{k}\centerdot {{e}_{i}}=\left[\begin{matrix} {{a}_{i11}}&\cdots &{{a}_{im1}} \\ {{a}_{i12}}&\cdots &{{a}_{im2}} \\ \vdots &\vdots &\vdots \\ {{a}_{i1n}}&\cdots &{{a}_{imn}} \\ \end{matrix} \right],$ | (10) |
| $ A_{j}^{'}=S_{ji}^{k}\centerdot {{e}_{j}}=\left[\begin{matrix} {{a}_{1j1}}&\cdots &{{a}_{mj1}} \\ {{a}_{1j2}}&\cdots &{{a}_{mj2}} \\ \vdots &\vdots &\vdots \\ {{a}_{1jn}}&\cdots &{{a}_{mjn}} \\ \end{matrix} \right]。$ | (11) |
Ai,Aj ′均为n×m矩阵,aijk1>0,则表示从起始车位状态i出发经过存取车路径k1可以直达车位状态s;aijk2>0,表示从车位状态s出发经过存取车路径k2可以到达目的地车位状态j。接着,检验车位状态i,j经过一次转换是否可以到达指定位置,可以通过检验起讫车状态i,j一次状态转换信息矩阵
| $ A_{ij}^{1}=\left( {{a}^{ijpq}} \right)m\times n={{A}_{i}}\ltimes {{\left( A_{j}^{'} \right)}^{T}}。$ | (12) |
是否为零矩阵来判断[14-17]。此时Ai表示从起点i可直达的车位状态信息矩阵,Aj ′表示可直达指定位置j的车位状态信息矩阵[7]。因此
| $ A_{ij}^{1}=\left[\begin{matrix} {{a}_{i11}}&\cdots &{{a}_{im1}} \\ {{a}_{i12}}&\cdots &{{a}_{im2}} \\ \vdots &\vdots &\vdots \\ {{a}_{i1n}}&\cdots &{{a}_{imn}} \\ \end{matrix} \right]?\left[\begin{matrix} {{a}_{1j1}}&\cdots &{{a}_{mj1}} \\ {{a}_{1j2}}&\cdots &{{a}_{mj2}} \\ \vdots &\vdots &\vdots \\ {{a}_{1jn}}&\cdots &{{a}_{mjn}} \\ \end{matrix} \right]。$ | (13) |
此时
| $ a_{pq}^{ij}=\sum\limits_{t=1}^{m}{{{a}_{itp}}\centerdot {{a}_{tjq}}}。$ | (14) |
若矩阵Aij1为非零矩阵,则一定存在非零元素
| $ a_{pq}^{ij}=\sum\limits_{t=1}^{m}{{{a}_{itp}}\centerdot {{a}_{tjq}}}>0。$ | (15) |
若min{ aitp+atjq| aitp, atjq>0;t=1, …, m; q=1, …, n}=ait′p′+at′jq′,则此时车位状态i,j一次状态转换最优路线为:从起始车位状态i出发通过编号为p′的路线到达车位状态t′,再由车位状态t′状态转换编号为p′的路径即可到达车位状态j,此时起讫车位状态i,j间运行距离为d=ait′p′+at′jq′[18-21]。
立体车库通过此算法将预留空位移动至目标车位与出入口之间,空出车位的运行通道,车位通过此通道向下(向上)移动至第6层,再转向向前移动至出入口。目标车位与第6层之间每一层车位运行此算法后都可将空位移动至目标车位上方(下方);第6层车位运行此算法后每一列都将空位移动至目标车位前方。
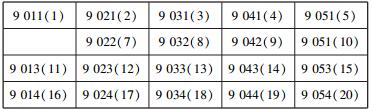
4 实验与结果如图 2所示,将立体车库俯视图看做4×5网络,车位9 011-9 014方向为路径1,车位9 021-9 024方向为路径2,车位9 031-9 034方向为路径3,车位9 041-9 044方向为路径4,车位9 051-9 054方向为路径5,9 011-9 041方向为路径6,9 012-9 042方向为路径7,9 013-9 043方向为路径8,9 014-9 044方向为路径9,共有20个车位。若初始车位为车位9 011,目的车位为车位9 023,查询起讫车位间的连接路径(假设所有路径为双向运行)。
 |
| 图 2 立体车库第9层俯视图 |
第1步,构造三维数组S={aijk|i, j=1, …, 20;k=1, …, 9}其中i,j表示立体车库中的车位,k表示立体车库中的移动线路。由立体车库结构图可知:
a121=1, a131=2, a141=3, a151=4, a231=1, a241=2, a341=1, a151=1, a211=1, a311=2, a411=3, a511=1, a321=1, a421=2, a431=1, a511=1, …a19189=1, a20199=1,其余aijk=0。
构造公交网络信息矩阵Sijk和Sjik,其中
| $ S_{ij}^{k}=\left[\begin{matrix} {{a}_{111}}\cdots {{a}_{1201}}&{{a}_{211}}\cdots {{a}_{2201}}&\cdots &{{a}_{2011}}\cdots {{a}_{20201}} \\ {{a}_{112}}\cdots {{a}_{1202}}&{{a}_{212}}\cdots {{a}_{2202}}&\cdots &{{a}_{2012}}\cdots {{a}_{20202}} \\ \vdots &\vdots &\vdots &\vdots \\ {{a}_{119}}\cdots {{a}_{1209}}&{{a}_{219}}\cdots {{a}_{2209}}&\cdots &{{a}_{2019}}\cdots {{a}_{20209}} \\ \end{matrix} \right],$ | (16) |
| $ S_{ji}^{k}=\left[\begin{matrix} {{a}_{111}}\cdots {{a}_{1201}}&{{a}_{211}}\cdots {{a}_{2201}}&\cdots &{{a}_{2011}}\cdots {{a}_{20201}} \\ {{a}_{112}}\cdots {{a}_{1202}}&{{a}_{212}}\cdots {{a}_{2202}}&\cdots &{{a}_{2012}}\cdots {{a}_{20202}} \\ \vdots &\vdots &\vdots &\vdots \\ {{a}_{119}}\cdots {{a}_{1209}}&{{a}_{219}}\cdots {{a}_{2209}}&\cdots &{{a}_{2019}}\cdots {{a}_{20209}} \\ \end{matrix} \right]。$ | (17) |
此时Sijk和Sjik是9行20×20列矩阵。
第2步,对于起始车位9 011和目的地车位9 023,判断两车位是否可以直达。首先,构造检验向量
| $ \begin{array}{l} {a_{120}} = S_{ij}^k\cdot{e_1}\cdot{e_{20}}\\ \left[{\begin{array}{*{20}{l}} {{a_{111}} \cdots {a_{1201}}}&{{a_{211}} \cdots {a_{2201}}}& \cdots &{{a_{2011}} \cdots {a_{20201}}}\\ {{a_{112}} \cdots {a_{1202}}}&{{a_{212}} \cdots {a_{2202}}}& \cdots &{{a_{2012}} \cdots {a_{20202}}}\\ {\;\;\;\;\;\;\;\;\; \vdots }&{\;\;\;\;\;\;\; \vdots }& \vdots &{\;\; \vdots }\\ {{a_{119}} \cdots {a_{1209}}}&{{a_{219}} \cdots {a_{2209}}}& \cdots &{{a_{2019}} \cdots {a_{20209}}} \end{array}} \right]\ltimes\\ \left[\begin{array}{l} 1\\ 0\\ \; \vdots \\ 0 \end{array} \right]\ltimes\left[\begin{array}{l} 0\\ 0\\ \; \vdots \\ 1 \end{array} \right.\left. {} \right] = \left[\begin{array}{l} {a_{1201}}\\ {a_{1202}}\\ \; \vdots \\ {a_{1209}} \end{array} \right], \end{array} $ | (18) |
其中,ep表示第p个坐标为1的20维单位列向量,由前面所得数组信息可以看出,检验数b19=a19Ta19=0,表明车位9 011(1) 与车位9 054(20) 之间不存在单向到达的线路。
第3步,考虑一次转向的情况。首先,单向到达车位信息矩阵:
| $ {{A}_{1}}=S_{ij}^{k}\ltimes{{e}_{1}}=\left[\begin{matrix} {{a}_{111}}&\cdots &{{a}_{1201}} \\ {{a}_{112}}&\cdots &{{a}_{1202}} \\ \vdots &\vdots &\vdots \\ {{a}_{119}}&\cdots &{{a}_{1209}} \\ \end{matrix} \right],$ | (19) |
| $ A_{_{20}}^{'}=S_{ji}^{k}\ltimes{{e}_{20}}=\left[\begin{matrix} {{a}_{1201}}&\cdots &{{a}_{20201}} \\ {{a}_{1202}}&\cdots &{{a}_{20202}} \\ \vdots &\vdots &\vdots \\ {{a}_{1209}}&\cdots &{{a}_{20209}} \\ \end{matrix} \right]。$ | (20) |
A1,A20′均为9×20矩阵。接着,检验车位9 011(1),9 054(20) 经过一次转向是否可以到达制定车位。构造起讫车位的一次转向信息矩阵
| $ A_{120}^{1}=\left( a_{pq}^{ij} \right)m\times n={{A}_{1}}\cdot {{\left( A_{_{20}}^{'} \right)}^{T}}。$ | (21) |
代入A1,A20′如图 3所示。
 |
| 图 3 构造起讫车位的一次转向信息矩阵 |
可得A1201如图 4所示。
 |
| 图 4 起讫车位的一次转向信息矩阵 |
起讫车位的一次转向信息矩阵A120不是零矩阵,表明车位1、20通过一次转向即可到达。此时非零元素a19由a151·a5209得到,也就是说一次转向路径为:从起始车位1出发,通过编号为1的线路到达车位5,接着转向编号为9的线路到达目的车位20,路径距离为d=a151+a5209=6;a45由a1165·a16204得到,也就是说一次转向路径为:从起始车位1出发,通过编号为5的路径到达车位16,接着转向编号为4的路径到达目的车位20,路径距离为d=a1165+a16204=6。此时最短距离相等,依照编号排序,最优一次转向路径为a19,通过编号为1的路径到达车位5,接着转向编号为9的路径到达目的车位20,路径距离为
| $ d={{a}_{151}}+{{a}_{5209}}=6。$ |
依照此算法得出的第9层到第7层的最优运行路径,即可空出车位向下至第6层移动通道;将车库正视图看作平面网络可得到车位第6层每一列的车位最优运行路线。通过以上运算可得到车位运行的最短路径,所需移动层车位同时按照各自最优路径运行,移动完成后空出目标车位与出口通道,该车位即可通过运行通道进行存取车操作。
通过以上运算可得到车位运行的最短路径,所述立体车库实际使用时,车主使用IC卡在刷卡位置刷卡,PLC控制器通过网络查询算法得到当前最近车位与最优路径,车位依照最优路径移动至出入口,车主将车放入车位,车主离开,车位移动放入车库。取车时,车主刷卡,对应车位依照最优路径移动至出入口,完成取车。使用本方法简化存取车路径,缩短了等待时间,提高了存取车效率。
5 结论基于半张量积立体车库网络调度算法研究首先将各层、各列的车位间位置信息存写至高维数组内,并组合为高维矩阵,借助半张量积运算得出路径转向信息矩阵,查询起讫车位直达、一次转向是否可以到达目的车位,在转向次数优先的前提下,得到起讫车位间的最优连接路线。不同于数据库查询算法的是,基于半张量积理论的查询方法将车位间连接情况的逻辑判断量化,使得查询过程可视化。存取车时不需计算全部层数,节省计算与车位移动时间,使运行效率最大化。
| [1] |
许光泞, 苑鸿骥, 林小峰. 立体车库计算机控制系统的构成及智能化方案[J]. 机电一体化, 2004(3): 34-36. |
| [2] |
李辰寅, 徐健, 张淑梅, 等. 立体停车库调度算法现[J]. 苏州科技学院学报(工程技术版), 2008, 21(1): 63-66. |
| [3] |
程代展, 赵寅, 徐听. 演化博弈与逻辑动态系统的优化控制[J]. 系统科学与数学, 2012, 32(10): 1226-1238. |
| [4] |
程代展, 齐洪胜. 矩阵的半张量积理论与应用[M]. 北京: 科学出版社, 2007.
|
| [5] |
程代展, 赵寅, 徐相如. 混合值逻辑及其应用[J]. 山东大学学报(理学版), 2011, 46(10): 32-44. |
| [6] |
葛爱冬. 基于矩阵半张量积方法的随机模糊系统控制器设计[J]. 山东大学学报(工学版), 2013, 43(3): 30-37. |
| [7] |
REN H L, GAO Z Y. Research on bi-level model and solutionalgorithm for dynamic transit design problem[J]. Systems Engineering-Theory&Practice, 2007(5): 81-89. |
| [8] |
刘旭浩, 徐勇. 基于半张量积理论的公交网络查询[J]. 复杂系统与复杂性科学, 2013, 10(1): 38-44. |
| [9] |
邓方安, 雍龙泉, 周涛, 等. 基于"矩阵乘法"的网络最短路径算法[J]. 电子学报, 2009, 7(37): 1594-1598. |
| [10] |
陈洁, 陆锋. 交通网络最短路径标号算法的实现与效率分析[J]. 中国图象图形学报, 2005, 10(9): 1134-1138. DOI:10.11834/jig.200509207 |
| [11] |
AZARON A. Bicriteria shortest path in networks of queues[J]. Applied Mathematics and Computation, 2006, 182(1): 43442. |
| [12] |
BRAESS D, NACKJRNEY A, WAKOLBINGER T. On a paradox of traffic planning[J]. Transportation Science, 2005, 39(4): 446-450. DOI:10.1287/trsc.1050.0127 |
| [13] |
FEILLET D, DEJAX P, GENDREAUG M. Traveling salesman problems with profit[J]. Transportation Science, 2005, 39(2): 188-205. DOI:10.1287/trsc.1030.0079 |
| [14] |
WINSTON W L. Operations Research[M]. UK: Duxbury Pr, 1994.
|
| [15] |
刘建强, 许雯, 刘粉林, 等. 一种最短路问题的遗传算法求解[J]. 数学实践与认识, 2007, 37(17): 53-58. |
| [16] |
赵建宏, 杨建宇, 雷维礼. 一种新的最短路径算法[J]. 电子科技大学学报, 2005, 34(6): 778-781. |
| [17] |
付翠玉, 关景泰. 立体车库发展的现状与挑战[J]. 机械设计与制造, 2005(9): 12-13. |
| [18] |
杨冬梅, 高炳学. 立体车库的布局设计[J]. 起重运输机械, 2003(5): 9-10. |
| [19] |
詹棠森, 张三强, 唐敏. 用矩阵和积求最短路的一种新算法[J]. 数学的实践与认识, 2006, 136(19): 170-172. |
| [20] |
王晟, 李乐民. 一种改进的多约束最佳路径算法研究[J]. 电子学报, 2004, 32(4): 529-535. |
| [21] |
HE H, ZHU D, MA S H. A New algorithm for the shortest paths computation by neural networks on time dependent networks[J]. Fudan University(Natural Science), 2004, 43(5): 714-716. |
 2017, Vol. 31
2017, Vol. 31


