| 基于线性规划的木板最优切割方案设计 |
在工厂生产或者是在家具的加工过程中, 常常需要将大块矩形板材(如钢板、木板、装饰板、包装纸等)切割成各种形状大小的板材[1], 因此研究板材的最优切割方案, 即用什么切割方案使得木板利用率最高, 获得最大利润, 是关键问题。二维木板切割下料问题属于NP难得组合优化问题, 在实际生活中有着广泛的应用。
木板最优切割问题按照优化目标的不同可分为约束二维剪切下料(TDGCS)及无约束二维剪切问题(UTDGC), 分别实现所切割的木板总面积最小及木板所排列毛坯的总价值最大。陈秋莲[2]以二维剪切下料问题为研究对象, 从以消耗的板材数量最少为目标的三阶段同质排样方案开始, 扩展到考虑余料标准化的排样方案, 最后研究了考虑余料标准化的余料下料问题;黄少丽[3]等求解二维下料问题基于价值修正策略的顺序启发式算法生成排样方案, 通过迭代生成多种排样方案进而从中选则最优的方案;易向阳[4]等采用经典背包算法提出一种切割工艺简单的新型排样方式即单毛坯条带四块排样方式, 排样方式价值高于传统的两段排样方式。因此, 本文基于国内外学者研究的基础上, 建立模型优化木板切割方案, 提高木板利用率, 实现生产任务, 实现总利润最大化。
1 背景叙述某家具厂新进一批木板如表 1所示需要使用切割工具切割为表 2所示产品, 结合问题给出木板最优切割方案。
| 表 1 待切割木板尺寸 |
 |
| 表 2 产品尺寸及生产任务 |
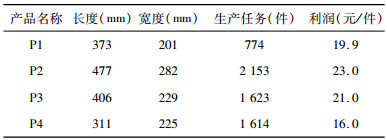 |
切割方案Ⅰ——在一块木板上切割P1产品, 给出按照木板利用率最高的切割方案;
切割方案Ⅱ——在完成表 2中的四种木材产品的生产任务条件下, 给出木板总利用率最高的切割方案;
切割方案Ⅲ——不考虑产品P1、P2、P3、P4的需求数量, 给定100张S1木板, 按照表 2中给出的利润, 建立数学模型, 给出总利润最大的切割方案。
2 数据来源及假设本文数据来源于2019数学建模五一联赛B题, 为了便于处理问题, 提出以下几条假设:(1)为保证较高的材料利用率, 切割方式采用正交切割;(2)切割时不考虑材料损耗与重叠;(3)按照产品尺寸的面积大小决定优先级的高低。先切割面积大的, 再切割面积小的, 能更好保证材料的利用率最大。
3 切割方案 3.1 切割方案Ⅰ 3.1.1 模型的建立给定的矩形产品P1置于长度为L, 宽度为W的木板S1上, 使得木板的利用率最高, 并满足一系列约束条件:两块产品之间互不重叠;产品P1必须放在木板S1上;满足一定的工艺要求。矩形件排列问题是从数学角度来分析线性规划问题, 实现目标函数最大化的同时满足其约束条件, 即木板利用率最高, 建立下列方程[5]:
决策变量:需要切割的产品种类为m1
目标函数:
| $ \max \eta = \frac{{{l_i} \cdot {w_i} \cdot {m_1}}}{{L \cdot W}} $ | (1) |
约束条件:
| $ \left\{ {\begin{array}{*{20}{l}} {{l_1} \cdot {m_1} \le L}\\ {{w_1} \cdot {m_1} \le W}\\ {{m_1} \ge 0} \end{array}} \right. $ | (2) |
根据上述的模型, 代入数据运用Lingo得到结果, 详见表 3。
| 表 3 切割方案Ⅰ切割数量和木板利用率表 |
 |
切割的方案如图 1所示:
 |
| 图 1 切割方案Ⅰ示意图 |
3.2 切割方案Ⅱ 3.2.1 模型的建立
为解决矩形件剪切下料问题, 我们将若干张长为L、宽为W的板材采用剪切工艺切割出m种矩形件, 裁剪长度为L0(W≤L0≤L);第i种需要切割产品的长、宽以及需求量分别为li、wi、di, 切割优化目标是耗费最少的板材张数在满足切出所需要的产品的数量下。
令Z为切割方案所使用的木材综述, G为每张板材上矩形件全部可能的切割方案数量, yj为第j种切割方案所切的板材总数, aij为第j种切割方式中含有的第i种切割产品的数量。针对该问题建立的数学模型为:
| $ \min Z = \sum\limits_{j = 1}^G {{y_j}} $ | (3) |
| $ \mathit{s}\mathit{.t}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {\sum\limits_{j = 1}^G {{a_{ij}}} {y_j} = {d_i},i = 1,2, \cdots ,m}\\ {{y_j} \in N,\quad \;\;\;j = 1,2, \cdots ,G} \end{array}} \right. $ | (4) |
(3) 式与(4)式中的最小化木材的切割张数是目标函数;第一行和第二行的约束条件分别表示为切割方案中每种产品的需求量均得到满足和每种木板所使用的张数均为自然数。
3.2.2 模型的求解蚁群算法[6-8]R(L, W, N)是长为L, 宽为W, 及数量为P的矩形玻璃原材料。
S={(l1, w1, p1), …(li, wi, pi)}是待切玻璃件的集合, n是待切玻璃的类型数, 第i类待切玻璃的长为li, 宽为wi, 数量为pi。问题是将给定规格的玻璃原材料切割成存在于集合S中的待切件, 使玻璃原材料的利用率最高, 废料率最少, 即
如下是蚁群算法的步骤:
Step1:输入原始数据S、R(L, W, N), ITER其中S={(l1, w1, p1), (l2, w2, p2), …(li, wi, pi)}为待切件的集合, R(L, W, N)为长为L, 宽为W, 数量为N的木板原料, ITER为循环的最大次数。
Step2:初始化数据, 设置参数α,β,ρ,q0, m的值, 其中α是初始参数, β是决定信息素和利用率的重要参数, ρ是一个有关信息素挥发度的参数(0≤ρ≤1), q1是[0, 1]上的参数, m是蚁群蚂蚁的数量。
Step3:计算初始信息素τ0, 并使每一个留在待切件i上的信息素τ(i)=τ0, 令全局最优解为0或者-1, 循环变量Q等于1。
Step4:根据转移规则τ(i)=(1-ρ)τ(i)+ρτ0和τ(i)=(1-α)τ(i)+αΔτ(i)对每一只蚂蚁从与或树的根节点出发选择一个待切件, 同时对其信息素进行局部更新, 直到从与或树到二叉树完成搜索, 然后暂时保存把结果二叉树相应的等待切件的链表。
Step5:找出当前最优的可行解在所有蚂蚁生成的暂时等待切件的链表中, 并给局部最优解变量值赋。
Step6:如果局部最优解大于全局最优解, 则把局部最优解的值赋值给全局最优解, 并把结果二叉树对应的待切件链表保存。
Step7:对于可行解的值等于局部最优解的链表中的待切件, 执行全局更新。
Step8:当循环变量Q等于循环的最大次数ITER, 程序结束, 并给出切割结果图和必要的数据。
参数的设置, 详见表 4。
| 表 4 蚁群算法参数设置表 |
 |
由以上模型, 在满足P1、P2、P3、P4产品生产任务的条件下, 求解出板材利用率最大时的最优切割方案如表 5所示。(表格中每行木板对应切割方案相同)
| 表 5 切割方案Ⅱ切割数量和木板利用率表 |
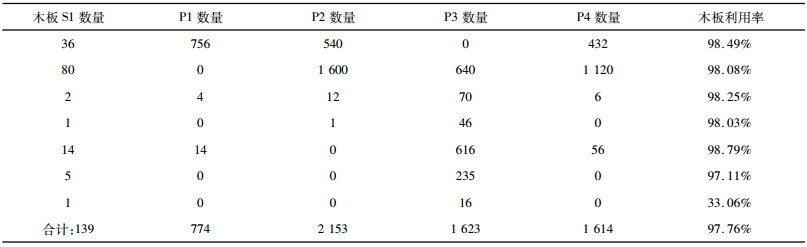 |
具体切割方式部分示意图, 如图 2所示。
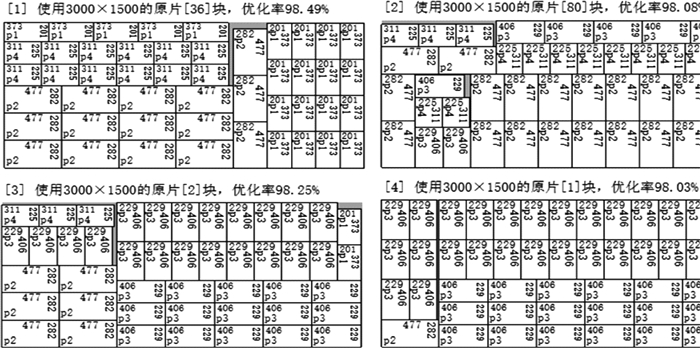 |
| 图 2 切割方案Ⅱ部分示意图 |
3.3 切割方案Ⅲ 3.3.1 模型的建立
为了解决板材二维无约束排样问题, 我们将规格为L(长)×W(宽)的板材切割成m种矩形件, 第i种矩形件规格为li×wi, 价值为vi, 其中对于每种矩形件的个数无约束;优化目标是使板材切割的矩形件总价值V最大。数学模型为[9-13]:
| $ \left\{ {\begin{array}{*{20}{l}} {V = \sum\limits_{i = 1}^m {{v_i}} {p_i}}\\ {s.t.P为一个合理的排样方式} \end{array}} \right. $ | (5) |
其中, pi为排样方式P中第i种矩形件的个数。二维无约束排样问题排样方案是由一组排样方式构成的, 其中每种排样方式都是由相应的排样算法生成, 采用线性规划方法来求解问题。其LP的求解步骤为:
Step1:构造一个初始可行解;
Step2:确定第i种矩形件当前价值, i=1, 2, …, m;
Step3:运用相应的TUP算法求解上述模型, 从而得到一个新的排样方式P;
Step4:当前排样方案中的一个排样方式用排样方式P置换, 当且仅当P能改善当前排样方案时, 转步骤2;否则转步骤5;
Step5:输出排样方案。
3.3.2 模型的求解采用LP求解排样方案, 其线性松弛模型为
| $ \left\{ {\begin{array}{*{20}{l}} {\min z = CX}\\ {s.t.AX \ge B}\\ {{\rm{X}} \ge 0} \end{array}} \right. $ | (6) |
其中, z为排样方案一共使用的板材面积;C=[C1, C2, …, Cm], 其中Ci=L·W(i=1, …, m); X=[x1, x2, …, xm]T, 其中A为排样方案m阶方阵;xi为第i种排样方式所使用的数量, 元素αij表示第j种排样方案中所含的第i种产品的个数;B=[b1, b2, …, bm]T, 其中bi为第i种产品的要求量。本文生成算法所使用的排样方案有以下7个步骤:
Step1:输入产品的尺寸和要求量数据li、wi、bi以及板材尺寸数据L、W。
Step2:可得到初始可行排样方案在令每张板材只排放一个第i种产品条件下, 该排样方案共使用
Step3:判断产品价值向量V=CA-1=[v1, v2, …, vm]。
Step4:根据各产品的价值, 调用排样方式生成算法, 从而构成一个新的排样方式P=[p1, p2, …, pm], pi表示该排样方案中包含第i种产品的个数。
Step5:运算引进P能否减少当前排样方案所用板材总面积z。
Step6:用P代替原有排样方案中的第k个排样方式, 其中k满足
Step7:输出最终排样方案。
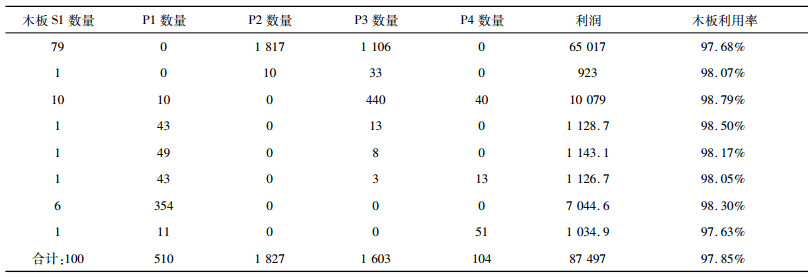
由以上模型, 求解出使得利润最大化时的最优切割方案, 并将结果填入表 6。
| 表 6 切割方案Ⅲ切割数量和木板利用率表 |
 |
.jpg) |
| 图 3(1) 切割方案Ⅲ部分示意图 |
.jpg) |
| 图 3(2) 切割方案Ⅲ部分示意图 |
3.4 结果分析
切割方案Ⅰ生产产品P1 59件, 木板利用率为98.79%;切割方案Ⅱ利用率排序前三的排样方式:P1的数量为30, P3的数量为23, 利用率为97.75%;P1的数量为42, P3的数量为13, 利用率为97.18%;P1的数量为30, P3的数量为23, 利用率为97.75%;切割方案Ⅲ总利润为87 497元, 木板总利用率达到97.85%。
4 结束语木板切割是二维面板下料的典型案例之一, 本文在三种不同的条件下分别采用线性规划、蚂蚁算法以及无约束下给出二位切割方案[14], 求得每个条件下的木板利用率最高的切割方案。本文所给出发散思维处理切割方案的方法不仅对现实二维板材下料具有指导意义, 而且触类旁通, 可以在生产生活中为一维的条材下料、三维立体型材料下料提供参考。这在当前我国经济从可持续发展深化向高质量发展提供较好的借鉴。
| [1] |
谭汉松, 彭迎春. 板材最优切割算法的设计与实现[J]. 计算机工程与应用, 2003(18): 95-96. DOI:10.3321/j.issn:1002-8331.2003.18.032 |
| [2] |
陈秋莲.二维剪切下料问题的三阶段排样方案优化算法研究[D].广州: 华南理工大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10561-1016771241.htm
|
| [3] |
黄少丽, 杨剑, 侯桂玉, 等. 解决二维下料问题的顺序启发式算法[J]. 计算机工程与应用, 2011, 47(13): 234-237. DOI:10.3778/j.issn.1002-8331.2011.13.066 |
| [4] |
易向阳, 仝青山, 潘卫平. 矩形件二维下料问题的一种求解方法[J]. 锻压技术, 2015, 40(06): 150-154. |
| [5] |
游凌伟.二维余料利用的下料算法研究[D].南宁: 广西大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10593-1015441451.htm
|
| [6] |
刘汉斌.基于遗传算法与蚁群算法的矩形排料研究[D].青岛: 青岛科技大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10426-1012324710.htm
|
| [7] |
于孜清.基于蚁群算法的玻璃切割控制系统[D].成都: 四川大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10610-2006188993.htm
|
| [8] |
张伟, 安鲁陵, 张臣, 等. 基于蚁群算法的矩形件切割路径优化[J]. 机械科学与技术, 2011, 30(3): 390-393. |
| [9] |
王严欣.应用精确两阶段排样图的板材下料算法[D].南宁: 广西大学, 2016. http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201705045.htm
|
| [10] |
潘卫平.矩形件二维剪切下料排样算法研究[D].南宁: 广西大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10593-1015441500.htm
|
| [11] |
曾兆敏, 王继红, 管卫利. 二维板材切割下料问题的一种确定性算法[J]. 图学学报, 2016, 37(4): 471-475. |
| [12] |
吕浈.玻璃切割优化排样系统设计与实现[D].武汉: 武汉理工大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10497-1012405644.htm
|
| [13] |
张玉泉. 二维切割板材特征参数及切割模式的选择[J]. 林业机械, 1994(1): 41-43. |
| [14] |
刘芃麦, 朱家明, 高正帅, 等. 基于BP神经网络的脱氧合金化配料问题分析[J]. 齐鲁工业大学学报, 2019, 33(5): 74-80. |
 2020, Vol. 34
2020, Vol. 34


