| 基于偶应力压电理论的双层矩形微板静态特性分析 |
2. 山东省机械设计研究院, 山东 济南 250031
2. Shandong Institute of Mechanical Design and Research, Jinan 250031, China
在很多微超声系统中, 压电微超声换能器PMUT(piezoelectric micromachined ultrasonic transducer)作为核心构件, 其性能直接影响超声系统的各项性能指标[1-3]。压电微超声换能器是层合结构, 它包含一个压电层、覆盖在压电层两侧的两个电极层, 以及一个弹性层组成[4], 其力学性能主要受到压电效应和尺寸微小化带来的尺寸效应的影响。经典力学理论不包含材料的长度特征参数, 无法解释尺寸效应, 因此许多学者提出了高阶理论来解释微构件的尺寸效应, 如偶应力理论和应变梯度理论。基于上述理论, 有许多单层微板的力学性能被广泛研究[5-8]。对于多层微板, 基于修正的偶应力理论, Chen等[9]研究了叠层Reddy微板的静态特性。Rahaeifard等[10]研究了双层微板的自由振动特性。基于应变梯度理论, Li等[11]分析了双层矩形微板的弯曲特性。但上述研究仅针对各向同性材料, 且模型中不包含压电层。随后, 对于微纳米尺度的压电结构, 其力学性能也被学者广泛研究[12-13]。
在上述研究中, 为简化模型, 只有压电材料的压电参数是各向异性的, 而其他材料参数依旧是各向同性的。研究发现, 许多压电材料如压电陶瓷PZT-4, 在极化之后展现出横观各向同性。为了研究横观各向同性压电材料的尺寸依赖特性, Wu[14]发展了针对横观各向同性压电材料的偶应力压电理论。基于该理论, Liu等[15]分析了双层压电微梁的力电耦合特性。然而, 现有研究对横观各向同性的压电微板研究较少, 从而使得PMUT的发展缺少理论据。因此, 研究横观各向同性双层微板的力学特性是非常有意义的。
在本文中, 我们考虑了PMUT的实际结构, 基于偶应力压电理论和Kirchahoff薄板理论, 建立了一个新型横观各向同性的压电双层矩形微板模型, 同时考虑了尺寸效应和压电效应的影响。基于该模型, 对中心挠度的尺寸依赖性、轴向应变和轴向应力的分布情况进行了详细的讨论分析。本模型可以对PMUT的设计提供有效的指导。
1 PMUT的结构模型考虑到PMUT结构中电极层的厚度比压电层和弹性层要小很多, 因此在本模型中忽略电极层的影响。建立了新型双层矩形微板的模型, 其中板的尺寸为a×b, 压电层和弹性层的厚度分别为h1和h2, 此外, 假设中性面的位置偏离接触面的距离为d。用载荷集度为q(x, y)的分布载荷表征实际应用中其它部件对PMUT的影响。微板的结构模型如图 1所示。
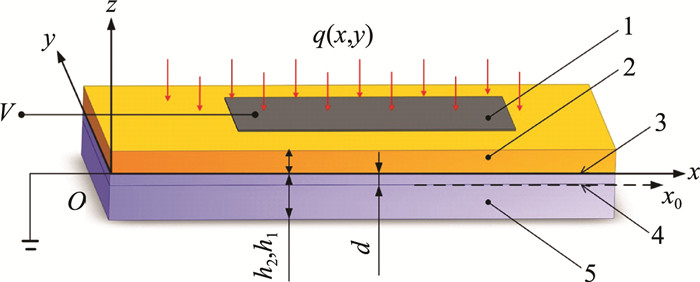 |
| 注: 1—电极层;2—压电层;3—接触面;4—中性面;5—弹性面。 图 1 双层矩形微板的结构 |
2 偶应力压电理论
基于偶应力压电理论, 不考虑挠曲电效应的能量密度可以写为应变εij, 旋转梯度张量的对称部分χijs和反对称部分κi以及极化强度Pi的函数[14]
| $ U=\frac{1}{2} \boldsymbol{a}_{i j k l} \varepsilon_{i j} \varepsilon_{k l}+\frac{1}{2} \boldsymbol{m}_{i j k l}^0 \chi_{i j}^s \chi_{k l}^s+\frac{1}{2} \boldsymbol{C}_{i j} \boldsymbol{\kappa}_i \boldsymbol{\kappa}_j+\frac{1}{2} \boldsymbol{k}_{i j} \boldsymbol{P}_i \boldsymbol{P}_j+\boldsymbol{D}_{i j k} \varepsilon_{i j} \boldsymbol{P}_k, $ | (1) |
其中, aijkl是材料弹性张量, mijkl0和Cij分别是与旋转梯度张量的对称和反对称部分相关的材料尺度张量。kij是电介质常数张量, Dijk是压电张量。公式(1)中的εij, χijs和κi可以写成
| $ {\varepsilon}_{i j}=\frac{1}{2}\left(\partial_i \boldsymbol{u}_j+\partial_j \boldsymbol{u}_i\right), $ | (2) |
| $ \chi_{i j}^s=\frac{1}{2}\left(\chi_{i j}+\chi_{j i}\right)=\frac{1}{2}\left(e_{i p q} \partial_p \varepsilon_{q j}+e_{j p q} \partial_p \varepsilon_{q i}\right), $ | (3) |
| $ \kappa_i=\frac{1}{2} e_{i j k} \chi_{k j}^a=\frac{1}{4} e_{i j k}\left(\chi_{i j}-\chi_{j i}\right)_{\circ} $ | (4) |
根据方程(1), 压电层本构关系可以表达为:
| $ \boldsymbol{\sigma}_{i j}^1=\frac{\partial U}{\partial \varepsilon_{i j}}=\boldsymbol{a}_{i j k l} {\varepsilon}_{k l}+\boldsymbol{D}_{i j k} \boldsymbol{P}_k, $ | (5) |
| $ \boldsymbol{m}_{i j}^{s 1}=\frac{\partial U}{\partial \chi_{i j}^s}=\boldsymbol{m}_{i j k l}^0 \chi_{k l}^s, $ | (6) |
| $ \boldsymbol{\mu}_i^1=\frac{\partial U}{\partial \kappa_i}=\boldsymbol{C}_{i j} \kappa_j, $ | (7) |
| $ \boldsymbol{E}_i=\frac{\partial U}{\partial \boldsymbol{P}_i}=\boldsymbol{k}_{i j} \boldsymbol{P}_j+\boldsymbol{D}_{k l i} {\varepsilon}_{k l}, $ | (8) |
其中, σij1是应力张量, mijs1和μi1分别是与旋转梯度张量的对称和反对称部分相关的高阶张量, Ei是电场强度。
对压电材料, 其电焓密度H可以写成内能密度、麦克斯韦电位梯度φ, i和极化强度的函数。
| $ H=U-\frac{1}{2} \varepsilon_0 \varphi_{, i} \varphi_{, i}+\varphi_{, i} \boldsymbol{P}_i, $ | (9) |
其中ε0是真空介电常数。
作为各向同性弹性材料, 弹性层的内能密度根据方程(1)可以写成
| $ U_2=\frac{1}{2} c_{i j} \varepsilon_{i j} \varepsilon_{k l}+m_{i j}^0 \chi_{i j}^s \chi_{k l}^s+\frac{1}{2} c_k \kappa_i \kappa_j。$ | (10) |
因此, 其本构方程可以写成:
| $ \boldsymbol{\sigma}_{i j}^{s 2}=\frac{\partial U}{\partial \varepsilon_{I j}}=c_{i j k l} \varepsilon_{k l}, $ | (11) |
| $ \boldsymbol{m}_{i j}^{s 2}=\frac{\partial U}{\partial \chi_{i j}^s}=m_{i j}^0 \chi_{k l}^s, $ | (12) |
| $ \boldsymbol{\mu}_i^{s 2}=\frac{\partial U}{\partial \boldsymbol{\kappa}_i}=c_{i j} {\kappa}_j 。$ | (13) |
如图 1所示, 假设中性层x0-y0偏离接触面x-y的距离为d, 对Kirchhoff板, 微板的位移场可以写为:
| $ \begin{aligned} & u(x, y, z)=-(d+z) \frac{\partial w(x, y)}{\partial x} \\ & v(x, y, z)=-(d+z) \frac{\partial w(x, y)}{\partial y} \\ & w=w(x, y) 。\end{aligned} $ | (14) |
双层矩形微板的非零应变分量在方程(2)中可写为
| $ \begin{aligned} & \varepsilon_{x x}=-(d+z) \frac{\partial^2 w}{\partial x^2} \\ & \varepsilon_{y y}=-(d+z) \frac{\partial^2 w}{\partial y^2} \\ & \varepsilon_{x y}=-(d+z) \frac{\partial^2 w}{\partial x \partial y} 。\end{aligned} $ | (15) |
按照弹性理论, 微板在纯弯曲的情况下其横截面的应力为0, 因此根据方程(5), (11)和(15), 可以得到距离d
| $ d=\frac{\left(c_{11}-c_{12}\right) h_2^2-\left(a_{11}-a_{12}\right) h_1^2}{2\left[\left(a_{11}-a_{12}\right) h_1+\left(c_{11}-c_{12}\right) h_2\right]} 。$ | (16) |
因此, 根据方程(1)和(9), 压电层的内能密度可以写出为
| $ \begin{gathered} H_1=\frac{1}{2} a_{11} \varepsilon_{x x} \varepsilon_{x x}+a_{12} \varepsilon_{x x} \varepsilon_{y y}+\frac{1}{2} a_{11} \varepsilon_{y y} \varepsilon_{y y}+a_{66} \varepsilon_{x y} \varepsilon_{x y}+m_{66}^0 \chi_{x y}^s \chi_{x y}^s+\frac{1}{2} c_2 \kappa_3 \kappa_3 \\ +\frac{1}{2} k_2 P_z P_z+D_{11} \varepsilon_{x x} P_z+D_{11} \varepsilon_{y y} P_z-\frac{1}{2} \varepsilon_0 \varphi_{, z} \varphi_{, z}+\varphi_{, z} P_{z 。} \end{gathered} $ | (17) |
对于弹性层来说, 其应变能密度能够根据方程(10)
| $ U_2=\frac{1}{2} c_{11} \varepsilon_{x x} \varepsilon_{x x}+c_{12} \varepsilon_{x x} \varepsilon_{y y}+\frac{1}{2} c_{11} \varepsilon_{y y} \varepsilon_{y y}+c_{13} \varepsilon_{x y} \varepsilon_{x y}+m_6^0 \chi_{x y}^s \chi_{x y}^s+\frac{1}{2} c_0 \kappa_3 \kappa_{3。} $ | (18) |
因此, 微板压电层和弹性层的总能量变分可以写成
| $ \delta \mathit\Theta=\delta\left(\int_0^{h_1} \int_0^a \int_0^b H_1\right)+\delta\left(\int_{-h_2}^0 \int_0^a \int_0^b U_2\right) 。$ | (19) |
分布载荷q(x, y)对外做功的变分为
| $ \delta W=\int_0^a \int_0^b q(x, y) \delta w \mathrm{d} x \mathrm{d} y 。$ | (20) |
基于变分原理, 由方程(17)-(20)可以得到以下方程
| $ \begin{gathered} \delta(\Theta-W)=-\int_0^a \int_0^b\left(\frac{\partial^2 M_x}{\partial x^2}+\frac{\partial^2 M_y}{\partial y^2}+2 \frac{\partial^2 M_{x y}}{\partial x \partial y}-q\right) \delta w \mathrm{d} x \mathrm{d} y-\left.\int_0^a M_y \delta w_y^{\prime}\right|_0 ^b \mathrm{d} x-\left.\int_0^b M_x \delta w_x^{\prime}\right|_0 ^a \mathrm{d} y \\ +\left.\int_0^a\left(\frac{\partial M_y}{\partial y}+2 \frac{\partial M_{x y}}{\partial x}\right) \delta w\right|_0 ^b \mathrm{d} x+\left.\int_0^b\left(\frac{\partial M_x}{\partial x}+2 \frac{\partial M_{x y}}{\partial y}\right) \delta w\right|_0 ^a \mathrm{~d} y+\int_0^{h_1} \int_0^a \int_0^b\left(E_z+\frac{\partial \varphi}{\partial z}\right) \delta P \mathrm{d} V \\ \quad+\int_0^{h_1} \int_0^a \int_0^b\left(\varepsilon_0 \frac{\partial^2 \varphi}{\partial z^2}-\frac{\partial P_z}{\partial z}\right) \delta P \mathrm{d} V+\left.\int_0^a \int_0^b\left(-\varepsilon_0 \frac{\partial \varphi}{\partial z}+P_z\right) \delta \varphi\right|_0 ^{h_1} \mathrm{d} x \mathrm{d} y=0, \end{gathered} $ | (21) |
其中, 弯矩Mx, My和扭矩Mxy表达为
| $ \begin{aligned} & M_x=M_x^1+M_x^2+M^E, \\ & M_y=M_y^1+M_y^2+M^E, \\ & M_{x y}=M_{x y}^1+M_{x y}^2, \end{aligned} $ | (22) |
其中, Mx1, My1和Mxy1是压电层的机械弯矩和扭矩, Mx2, My2和Mxy2是弹性层的力矩, ME代表电力矩。对于压电层, 其力矩可以定义为
| $ \begin{aligned} & M_x^1=\int_0^{h_1}\left[(d+z) \sigma_{x x}^1+m_{x y}^{s 1}+\frac{1}{2} \mu_z^1\right] \mathrm{d} z, \\ & M_y^1=\int_0^{h_1}\left[(d+z) \sigma_{y y}^1-m_{x y}^{s 1}+\frac{1}{2} \mu_z^1\right] \mathrm{d} z, \\ & M_{x y}^1=\int_0^{h_1}(d+z) \sigma_{x y}^1 \mathrm{~d} z, \\ & M^E=\int_0^{h_1}(d+z) \sigma^E d z=\int_0^{h_1}(d+z) D_{11} P_z \mathrm{~d} z 。\end{aligned} $ | (23) |
弹性层的力矩可以定义为
| $ \begin{aligned} & M_x^2=\int_{-h_2}^0\left[(d+z) \sigma_{x x}^2+m_{x y}^{s 2}+\frac{1}{2} \mu_z^2\right] \mathrm{d} z, \\ & M_y^2=\int_{-h_2}^0\left[(d+z) \sigma_{y y}^2-m_{x y}^{s 2}+\frac{1}{2} \mu_z^2\right] \mathrm{d} z, \\ & M_{x y}^2=\int_{-h_2}^0(d+z) \sigma_{x y}^2 \mathrm{~d} z_{\circ} \end{aligned} $ | (24) |
电弯矩ME的影响通常并不显著[14], 因此在后续分析中将其忽略。根据方程(21), 双层微板的控制方程表达为
| $ \begin{aligned} & \frac{\partial^2 M_x}{\partial x^2}+\frac{\partial^2 M_y}{\partial y^2}+2 \frac{\partial^2 M_{x y}}{\partial x \partial y}-q=0, \\ & E_z+\frac{\partial \varphi}{\partial z}=0, \\ & \varepsilon_0 \frac{\partial^2 \varphi}{\partial z^2}-\frac{\partial P_z}{\partial z}=0_{。} \end{aligned} $ | (25) |
并且简支双层板的边界条件为
| $ \begin{aligned} & \left.M_y \delta w_y^{\prime}\right|_0 ^b=0, \\ & \left.M_x \delta w_x^{\prime}\right|_0 ^a=0, \\ & \left.\left(\frac{\partial M_y}{\partial y}+2 \frac{\partial M_{x y}}{\partial x}\right) \delta w\right|_0 ^b=0, \\ & \left.\left(\frac{\partial M_x}{\partial x}+2 \frac{\partial M_{x y}}{\partial y}\right) \delta w\right|_0 ^a=0, \\ & \left.\left(-\varepsilon_0 \frac{\partial \varphi}{\partial z}+P_z\right) \delta \varphi\right|_0 ^{h_1}=0 \text { 。} \end{aligned} $ | (26) |
将压电层的本构关系方程(5)~(8)以及弹性层的本构关系方程(11)~(13)带入方程(25), 得到挠度形式的控制方程为
| $ \begin{aligned} & \left(a_{11} I_1+c_{11} I_2\right) \frac{\partial^4 w}{\partial x^4}+\left(a_{11} I_1+c_{11} I_2\right) \frac{\partial^4 w}{\partial y^4}+2\left[\left(a_{12}+a_{66}\right) I_1+\left(c_{12}+c_{13}\right) I_2\right] \frac{\partial^4 w}{\partial x^2 \partial y^2} \\ & +\frac{1}{2}\left(m_{66}^0 h_1+m_6^0 h_2\right)\left(\frac{\partial^4 w}{\partial x^4}+\frac{\partial^4 w}{\partial y^4}-2 \frac{\partial^4 w}{\partial x^2 \partial y^2}\right)+\frac{1}{4}\left(c_2 h_1+c_0 h_2\right)\left(\frac{\partial^4 w}{\partial x^4}+\frac{\partial^4 w}{\partial y^4}+2 \frac{\partial^4 w}{\partial x^2 \partial y^2}\right)=q(x, y), \end{aligned} $ | (27) |
| $ k_2 P_z-D_{11} z\left(\frac{\partial^2 w}{\partial x^2}+\frac{\partial^2 w}{\partial y^2}\right)+\frac{\partial \varphi}{\partial z}=0, $ | (28) |
| $ \varepsilon_0 \frac{\partial^2 \varphi}{\partial z^2}-\frac{\partial P_z}{\partial z}=0, $ | (29) |
其中
| $ \begin{aligned} & I_1=d^2 h_1+d h_1^2+\frac{h_1^3}{3}, \\ & I_2=d^2 h_2-d h_2^2-\frac{h_2^3}{3} 。\end{aligned} $ | (30) |
方程(27)为微板的力学控制方程, (28)与(29)为微板的电学控制方程, 本文中仅讨论微板的力学性能。因此, 微板的挠度可以在方程(27)中通过傅里叶级数的方法得到, 可以使用三角函数傅里叶级数作为试函数
| $ w(x, y)=\sum\limits_\limits{m=1}^{\infty} \sum\limits_\limits{n=1}^{\infty} A_{m n} \sin \left(\frac{m \pi x}{a}\right) \sin \left(\frac{n \pi y}{b}\right), $ | (31) |
其中Amn是与m和n相关的傅里叶系数。方程(31)符合简支矩形板的边界条件。而且q(x, y)也可以用傅里叶级数表示[11]
| $ q(x, y)=\sum\limits_\limits{m=1}^{\infty} \sum\limits_\limits{n=1}^{\infty} Q_{m n} \sin \left(\frac{m \pi x}{a}\right) \sin \left(\frac{n \pi y}{b}\right) $ | (32) |
如果载荷q(x, y)是一个等于q0的均布载荷, Qmn可以表达为
| $ Q_{m n}=\frac{16 q_0}{m n \pi^2} \quad m, n=1,3,5, \cdots,$ | (33) |
把傅里叶级数方程(31)和(32)代入控制方程(27), 傅里叶系数可以推导为
| $ A_{m n}=\frac{4 Q_{m n}}{4 P_1+4 P_2+8 P_3+2 P_4+P_5}, $ | (34) |
其中,
| $ \begin{aligned} & P_1=\left(a_{11} I_1+c_{11} I_2\right)\left(\frac{m \pi}{a}\right)^4, \\ & P_2=\left(a_{11} I_1+c_{11} I_2\right)\left(\frac{n \pi}{b}\right)^4, \\ & P_3=\left[\left(a_{12}+a_{66}\right) I_1+\left(c_{12}+c_{13}\right) I_2\right]\left(\frac{m \pi}{a}\right)^2\left(\frac{n \pi}{b}\right)^2, \\ & P_4=\left(m_{66}^0 h_1+m_6^0 h_2\right)\left[\left(\frac{m \pi}{a}\right)^4+\left(\frac{n \pi}{b}\right)^4-2\left(\frac{m \pi}{a}\right)^2\left(\frac{n \pi}{b}\right)^2\right], \\ & P_5=\left(c_2 h_1+c_0 h_2\right)\left[\left(\frac{m \pi}{a}\right)^4+\left(\frac{n \pi}{b}\right)^4+2\left(\frac{m \pi}{a}\right)^2\left(\frac{n \pi}{b}\right)^2\right] 。\end{aligned} $ | (35) |
把傅里叶系数方程(34)和(35)代入试函数方程(31), 即可得到挠度w。
4 数值结果及讨论对于压电微超声换能器, 其压电层采用的横观各向同性材料通常为PZT-4, 弹性层采用的各向同性材料一般为Si。定义PZT-4层的无量纲厚度为h1/l1, Si层的无量纲厚度为h2/l2, 其中l1和l2分别为该两层的长度尺度参数, 为简化计算, 假设l1=l2=l=1 μm。PZT-4和Si的材料参数[16-18]为: a11=139 GPa, a12=77.8 GPa, a44=25.6 GPa, a66=30.6 GPa, m660=a66l12, c2=a66l12, c0=c13l22, c11=165.7 GPa, c12=63.9 GPa, c13=79.6 GPa, m60=c13l22, k2=1.828×108(V·m)/C, D11=-1.28×109 V/m, ε0=8.85×10-12C/(V·m)。当取m=n=31时, 可以获得足够精度的计算结果[11]。文献[11]利用应变梯度弹性理论研究了一种双层微板。为了解释压电层与弹性层厚度比(β=h1/h2)对结果的影响, 文献[11]中定义无量纲相对厚度t为
| $ t=\frac{h_1-h_2}{\sqrt{h_1 h_2}}=\frac{\beta-1}{\sqrt{\beta}}, $ | (36) |
同时, 为了将现有模型与其做比较, 假设旋转梯度张量的反对称部分为κi=0, 并且让现有微板模型的尺寸与其保持一致, 即a=b=30 μm, 厚度为2.4 μm。图 2显示了微板的中心挠度与无量纲相对厚度t的变化关系。
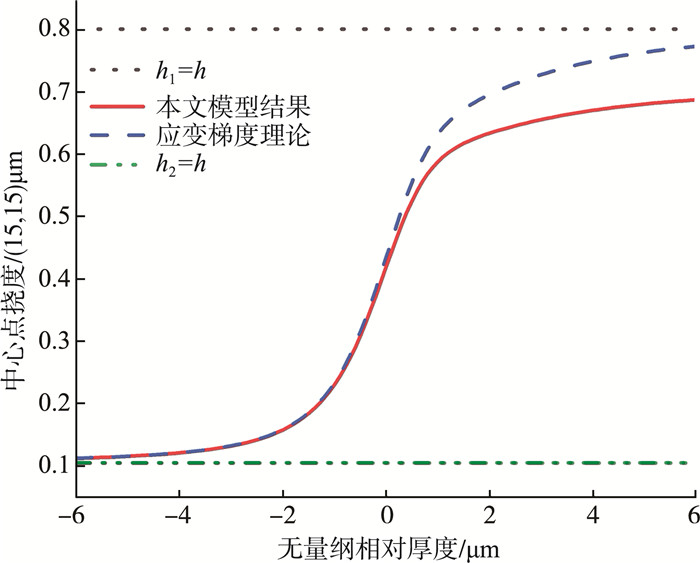 |
| (q0=10 μN, V=10 mV) 图 2 中心挠度随无量纲相对厚度t的变化(与文献[11]对比) |
从图 2可看出, 中心挠度随无量纲相对厚度t的增大而增大。如果双层微板中的其中一层比另外一层厚的多, 微板的挠度将会接近单层板。当无量纲相对厚度t远大于1时, 本文模型的结果比现有文献的结果要小。与文献[11]的模型相比, 本文模型由于考虑了压电效应与横观各向同性材料的影响, 会使压电层具有较大的刚性, 从而导致中心挠度的降低。
图 3表现了无量纲厚度h/l对横观各向同性压电微板的中心点挠度w的影响。从图中可以看出, 当长宽比a/b小于2时, 中心点挠度随着比值的增大而大幅升高, 当长宽比a/b大于2时, 中心点挠度随比值增大缓慢上升。此外, 当a/b的比值一定时, 中心挠度w随着h/l的增大而显著增大。可见长宽比小于2时, 其比值变化对微板刚度的影响较为明显。结果表明, 为了获得更大的中心挠度w, 在选用横观各向同性压电双层矩形微板时, 我们可以选择比值a/b大于2的, 或者具有较小的长度尺度参数的微板。
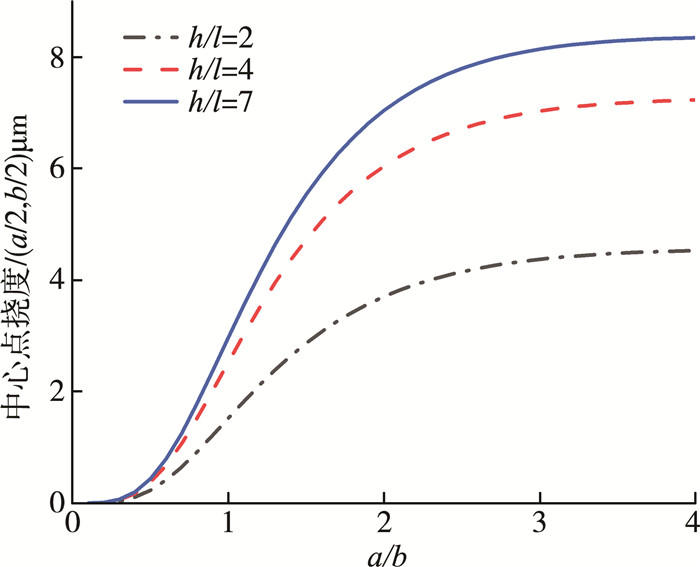 |
| 图 3 不同h/l时中心挠度随长宽比a/b的变化 |
在双层微板的中心点处, 轴向应力σxx随厚度的变化以及与经典理论的比较如图 4所示。从图 4可看出轴向应力的分布是分段的, 在每一段中, 轴向应力σxx随微板高度方向坐标z的增加而显著增大。同时可以明显看出轴向应力与微板厚度值成线性关系, 而在压电层和弹性层之间的界面处会发生跳变, 这是因为两层材料的属性在界面处发生变化。此外, 可以进一步注意到, 与经典理论的结果相比(mijkl0=0, kij=0, Cij=0), 当微板厚度h近似于长度尺度参数l时, 基于本模型的轴向应力将会明显减小。
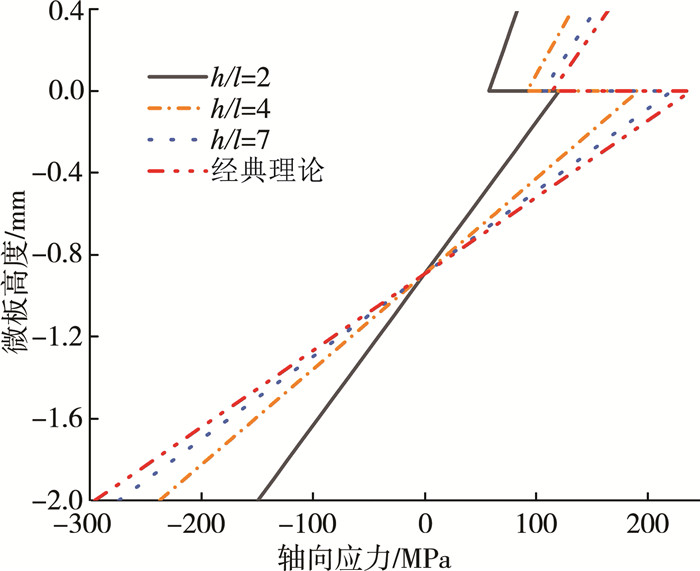 |
| (q0=10 μN, V=10 mV, t=0.2) 图 4 在不同h/l下轴向应力分布随双层微板高度的变化 |
双层微板中心截面的挠度分布如图 5所示, 微板挠度一般在中心区域达到最大, 参数比h/l对中间部分的挠度有明显的影响, 即挠度随着比值h/l的减小而减小。此外, 与经典模型的结果相比, 当厚度h近似于参数l时, 挠度将会明显减小。
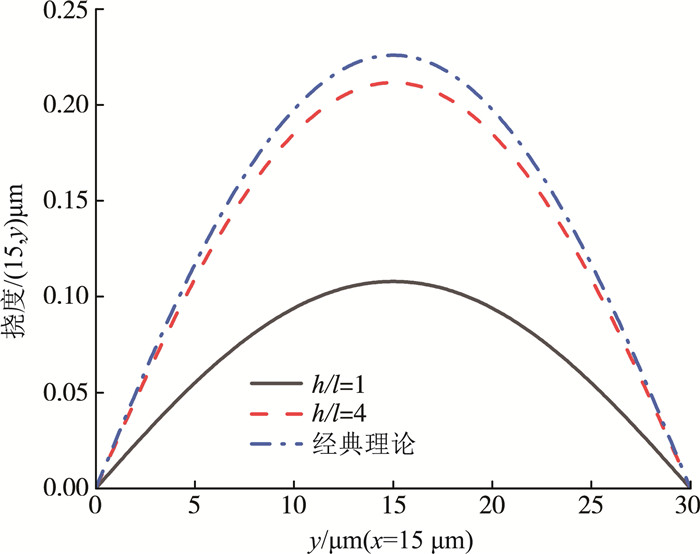 |
| (h=2.4 μm, β=2, V=10 V) 图 5 x=15 μm时中心截面上的挠度分布 |
5 结论
本文采用偶应力压电理论针对横观各向同性材料建立了一个新的双层矩形微板的力学模型。基于该模型, 研究了均布荷载作用下简支双层微板的静态特性。数值结果阐明了以下几个方面: (1)当无量纲相对厚度t > 1时, 本模型的计算结果明显小于应变梯度理论的计算结果。(2)当长宽比a/b < 2时, 中心点挠度随着比值a/b的增大而显著增大;当长宽比a/b > 2时, 中心点挠度随着a/b的增大而缓慢增大。对于确定的比值a/b, 中心挠度随着h/l的增大明显增大。(3)轴向应力的分布是分段的, 会在压电层与弹性层之间的界面处发生跳变。当双层微板的厚度接近参数l时, 轴向应力会明显减小。(4)h/l的比值对中心挠度有密切的影响。当厚度h接近参数l时, 挠度将会明显减小。
| [1] |
SUZUKI M, TAGAWA N, YOSHIZAWA M, et al. Effects of flexural vibration and thickness vibration on receiving characteristics of a diaphragm-type PZT resonator[J]. Japanese Journal of Applied Physics, 2020, 59(SK): SKKE10. DOI:10.35848/1347-4065/ab80a0 |
| [2] |
LIU W J, HE L M, WANG X B, et al. 3D FEM analysis of high-frequency AlN-based PMUT arrays on cavity SOI[J]. Sensors, 2019, 19(20): 4450. DOI:10.3390/s19204450 |
| [3] |
余卿, 遆金铭, 樊青青, 等. 压电微机械超声换能器仿真与结构优化[J]. 压电与声光, 2022, 44(3): 403-406. DOI:10.11977/j.issn.1004-2474.2022.03.014 |
| [4] |
DANGI A, PRATAP R. System level modeling and design maps of PMUTs with residual stresses[J]. Sensors and Actuators A: Physical, 2017, 262: 18-28. DOI:10.1016/j.sna.2017.05.006 |
| [5] |
HUANG Y, KARAMI B, SHAHSAVARI D, et al. Static stability analysis of carbon nanotube reinforced polymeric composite doubly curved micro-shell panels[J]. Archives of Civil and Mechanical Engineering, 2021, 21(4): 139. DOI:10.1007/s43452-021-00291-7 |
| [6] |
SHARIATI A, HABIBI M, TOUNSI A, et al. Application of exact continuum size-dependent theory for stability and frequency analysis of a curved cantilevered microtubule by considering viscoelastic properties[J]. Engineering With Computers, 2021, 37(4): 3629-3648. DOI:10.1007/s00366-020-01024-9 |
| [7] |
SHAAT M, MAHMOUD F F, GAO X L, et al. Size-dependent bending analysis of Kirchhoff nano-plates based on a modified couple-stress theory including surface effects[J]. International Journal of Mechanical Sciences, 2014, 79: 31-37. DOI:10.1016/j.ijmecsci.2013.11.022 |
| [8] |
徐晓建, 邓子辰. 基于简化的应变梯度理论下Kirchhoff板模型边值问题的提法及其应用[J]. 应用数学和力学, 2022, 43(4): 363-373. |
| [9] |
CHEN W J, XU M, LI L. A model of composite laminated Reddy plate based on new modified couple stress theory[J]. Composite Structures, 2012, 94(7): 2143-2156. DOI:10.1016/j.compstruct.2012.02.009 |
| [10] |
RAHAEIFARD M, MOJAHEDI M. On the mechanics of laminated microplates[J]. International Journal of Engineering Science, 2017, 119: 180-188. DOI:10.1016/j.ijengsci.2017.06.003 |
| [11] |
LI A Q, ZHOU S J, ZHOU S S, et al. A size-dependent model for bi-layered Kirchhoff micro-plate based on strain gradient elasticity theory[J]. Composite Structures, 2014, 113: 272-280. DOI:10.1016/j.compstruct.2014.03.028 |
| [12] |
LOU J, HE L W, DU J K, et al. Buckling and post-buckling analyses of piezoelectric hybrid microplates subject to thermo-electro-mechanical loads based on the modified couple stress theory[J]. Composite Structures, 2016, 153: 332-344. DOI:10.1016/j.compstruct.2016.05.107 |
| [13] |
KORAYEM M H, HOMAYOONI A. The size-dependent analysis of multilayer micro-cantilever plate with piezoelectric layer incorporated voltage effect based on a modified couple stress theory[J]. European Journal of Mechanics-A/Solids, 2017, 61: 59-72. DOI:10.1016/j.euromechsol.2016.08.013 |
| [14] |
吴康辉. 含挠曲电效应的横观各向同性压电材料偶应力理论[D]. 济南: 山东大学, 2018.
|
| [15] |
LIU Y, ZHOU S J, WU K H, et al. Size-dependent electromechanical responses of a bilayer piezoelectric microbeam[J]. International Journal of Mechanics and Materials in Design, 2020, 16(3): 443-460. DOI:10.1007/s10999-019-09478-6 |
| [16] |
KANG X, YANG F J, HE X Y. Nonlinearity analysis of piezoelectric micromachined ultrasonic transducers based on couple stress theory[J]. Acta Mechanica Sinica, 2012, 28(1): 104-111. DOI:10.1007/s10409-012-0019-5 |
| [17] |
LI Y S, PAN E. Static bending and free vibration of a functionally graded piezoelectric microplate based on the modified couple-stress theory[J]. International Journal of Engineering Science, 2015, 97: 40-59. DOI:10.1016/j.ijengsci.2015.08.009 |
| [18] |
ZHANG L, BARRETT R, CLOETENS P, et al. Anisotropic elasticity of silicon and its application to the modelling of X-ray optics[J]. Journal of Synchrotron Radiation, 2014, 21(Pt 3): 507-517. |
 2023, Vol. 37
2023, Vol. 37


