| 经典分子动力学模拟在矿物浮选研究中的应用 |
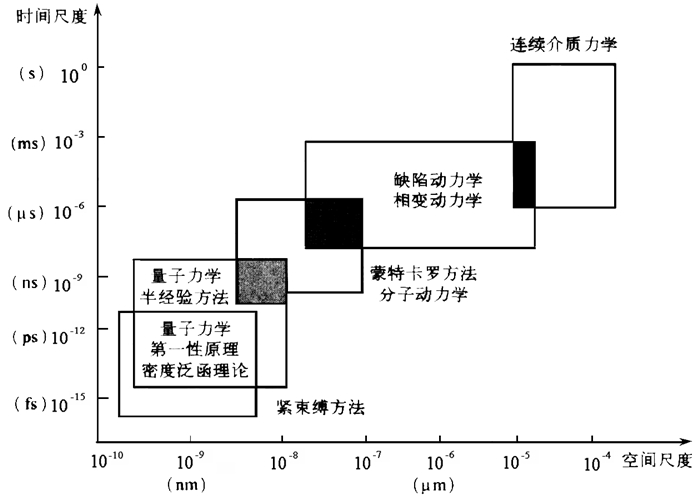
“材料计算与设计”的思想产生于20世纪50年代,随着计算科学与技术的飞速发展,理论和计算在科学研究过程中的作用越来越大。一方面是模拟计算,即根据材料学和相关学科基本原理,从实际数据出发,通过建立数学模型及数值计算,模拟实际过程;另一方面是材料理论计算与设计,即直接通过理论的物理模型和数值计算,预测或设计材料结构与性能。电子、原子和分子水平上的物质结构及其物性研究是科技发展的重大基础研究问题之一,不同尺度、不同层次、不同范畴内所使用的理论方法不同,图 1所示为不同时间、空间尺度与理论研究方法的对应关系。
由图 1可见,不同的时间和空间尺度范畴内所用的理论方法不同,从基于量子力学和密度泛函理论的第一性原理计算到分子动力学和蒙特卡罗模拟,然后是缺陷动力学、相变动力学,再向连续介质力学方法过渡[1]。
分子动力学模拟,一般指的是经典分子动力学模拟,是在原子层面通过对体系的结构和动力学参数进行计算和统计分析,研究体系以及体系中分子或者原子相关性质的方法[2]。自1957年Alder和Wainwright[3]首次采用分子动力学研究物质的宏观性质,分子动力学模拟已广泛应用于物理、化学、材料和生物等学科的研究[4-8]。经典分子动力学方法的物理思想是用差分近似法求解牛顿运动方程,并追踪系统的时间变化,可以通过模拟分子的结构和分子间相互作用力来研究分子的物化性质,直观展示分子间相互作用以及模拟的动态过程;并结合现代先进的实验、检测分析手段,实现物质结构以及分子间相互作用的宏观与微观展示[1, 9]。
经典分子动力学模拟以原子为最小研究单元,忽略电子运动,采用经典力学原理分析原子或者分子之间的相互作用,计算速度较快,可用来预测体系的平衡构型和能量,或具有大分子的平衡体系的动力学和热力学性质,是联结体系微观状态、演变以及宏观性质的桥梁[10, 11]。1985年,Car R和Parrinello M成功将经典分子动力学模拟和密度泛函理论有机结合起来,首次提出了第一性原理分子动力学计算方法[1, 12]。将经典的牛顿力学扩展到薛定谔方程,使用量子力学描述电子状态,并将经典分子动力学和密度泛函理论有机结合来描述体系中化学键的形成和断裂,扩展了分子模拟应用的深度和广度[13, 14]。
作为凝聚态物理学常用的计算机模拟技术,经典分子动力学模拟可以在传统选矿方法和检测手段的基础上,直观展示并量化矿物晶体结构、药剂分子结构和矿物与药剂分子之间的相互作用等相关参数,为浮选研究提供理论依据,其在矿物浮选研究中的应用,主要包括对矿物晶体化学、浮选溶液化学、浮选电化学、表面化学等性质的研究,以及浮选药剂分子的设计等[15]。
本文整理了近年来基于经典分子动力学模拟进行的矿物浮选研究成果,综述了矿物浮选研究过程中分子动力学模拟的应用方向。
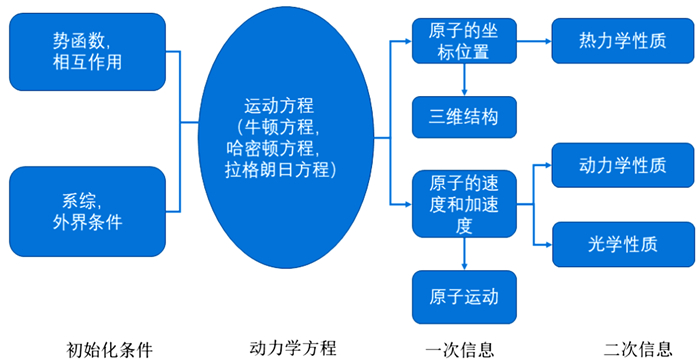
1 经典分子动力学模拟简介 1.1 经典分子动力学基本原理经典分子动力学模拟的基本思想如图 2所示,即通过数值积分求解牛顿运动方程,记录模拟体系中粒子位置和速度随时间变化的轨迹,并依据轨迹采用统计力学方法获得体系的宏观性质[16]。
分子动力学模拟假定每一个分子都遵从经典力学运动定律,并且分子之间的相互作用满足叠加定理[17]。分子力学忽略体系的电子结构,将不同原子坐标位置的体系作用能用一系列解析函数表示,从典型的结构参数和作用力角度研究体系性质,即用位能函数表示在模拟体系中键长、键角、二面角等结构参数和非键相互作用能,体系总能量则为体系内所有分子或原子的势能和动能的总和[18]。经典力学中,势能的梯度即为体系中分子或原子所受的力。因此,经典分子动力学模拟以牛顿运动定律为理论基础,通过统计计算各个分子或原子的位置来计算总势能,计算出各个分子或原子所受的范德华力,求得加速度,进而得到一定时间后各个分子或原子的速度和位置,最终得到不同时刻分子或者原子的位置、加速度和速度,即运动轨迹,进而得到分子体系的宏观物理量[19]。
基于分子体系的经典力学模型,分子动力学模拟可以优化分子总能量得到稳定构型,反复采集分子体系位形空间样本,计算得到体系的总能量,然后在体系最优构型基础上分析平衡性质[20]。
1.2 力场经典分子动力学模拟基于分子力学,用经典力学方程求解核运动,采用力场方法模拟计算原子或分子之间的相互作用[21]。分子力学将势能进行经验拟合成力场,因此可将表达原子间相互作用的势能函数统称为分子力场[22]。力场是以数学形式表示的分子势能函数,是分子动力学模拟的基础,主要由原子类型列表、势函数和力场参数三部分组成[23]。力场从原子类型、杂化方式以及电荷等方面区分不同体系中的原子,不同的力场包含不同的原子类型列表和势能函数,势能函数以解析式的形式描述粒子间的相互作用,包含:
键伸缩能Ec:构成分子的各个化学键在键轴向上的伸缩运动所引起的能量变化;
键角弯曲能Eb:键角变化引起的分子能量变化;
二面角扭转能Et:单键旋转引起分子骨架扭曲所产生的能量变化;
非键能Enb:包括范德华力、静电相互作用等与能量有关的非键相互作用;
交叉能量相:上述作用之间耦合引起的能量变化。
力场参数包括平衡键长、键角、二面角等,可通过试验测得或量子化学计算得出,分子的总势能可表示为[18, 24]:
| $ E = {E_{nb}} + {E_b} + {E_c} + {E_t} + \cdots $ | (1) |
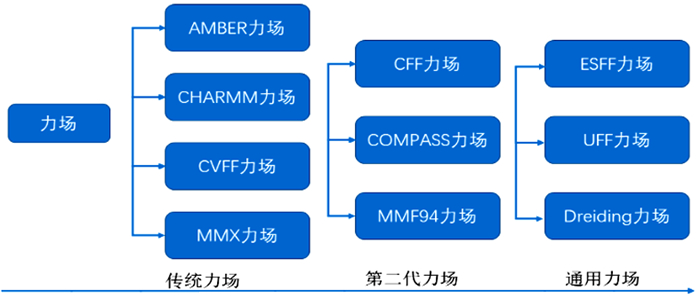
在分子动力学模拟过程中,合适力场的选择决定了模拟结果的可靠性[25]。分子动力学模拟中力场的发展和分类如图 3所示。其中传统力场主要有:AMBER力场、CHARMM力场、MMX力场和CVFF力场等[26-29]。第二代力场势能函数比传统力场复杂,主要包括:CFF力场、COMPASS力场、UFF力场和Dreiding力场等[30-32]。除上述力场外,还有一些基于常用力场为特定体系构建的特殊力场[33]。
1.3 系综
经典分子动力学模拟是通过求解牛顿运动方程对体系进行模拟,不同的体系要求产生了系综。系综是具有相同条件系统的集合,可分为正则系综(NVT)、微正则系综(NVE)、等温等压系综(NTP)等[33, 34]。正则系综,为具有相同分子数N、相同体积V与相同温度T的系统的集合,以符号(NVT)表示;微正则系综(NVE),E为系统的能量;等温等压系综(NTP),P为系统的压力;巨正则系综(μVT),μ为系统的化学势能。不同系综条件下,根据系综的原子数、压强、温度、体积、能量等性质,可以计算体系的结构、能量以及动力学性质[36]。实际应用中,不同的体系需选取适当的系综,系综越大,所含的分子数目越多,误差越小[35]。
2 经典分子动力学模拟在矿物浮选中的应用影响矿物浮选效果的主要因素包括矿物性质、浮选药剂性能及溶液条件和浮选界面组成等。矿物本身的晶体结构、解理面决定了矿物在浮选溶液中的表面性质,浮选药剂及溶液的物理化学性质决定了药剂或溶液离子在矿物表面的吸附。溶液中药剂或者离子作用在矿物表面,即形成了浮选界面,浮选界面主要涉及浮选界面电荷转移、矿物表面药剂分子的取向和矿物表面分子间或分子内的作用等。浮选中的经典分子动力学模拟可以在分子层面直观展示矿物晶体和表面结构、浮选药剂吸附构型、矿物与浮选药剂之间的相互作用等,通过药剂吸附形态解释浮选药剂作用机理[37, 38]。
2.1 矿物表面性质基于矿物表面性质的经典分子动力学模拟,可以研究矿物表面原子及其对表面性质的影响,也可以研究矿物表面及其原子的水化和表面润湿性,为矿物表面性质分析及药剂筛选提供理论依据,并解释矿物在特定浮选体系中的浮选行为。
矿物晶体结构的经典分子动力学模拟与实验结果具有较高的一致性,故可用分子动力学模拟突破实验条件的局限,定向探索晶体结构及其缺陷等,探究宏观表面化学理论无法解释的矿物表面及原子的水化和矿物晶体表面各向异性等。闵凡飞等[39]基于分子动力学模拟研究了煤泥水中高岭石和蒙脱石表面的水化,通过对界面原子浓度等的研究,探究水分子在高岭石和蒙脱石表面的扩散,研究水分子层厚度,并对二者水化程度和矿物表面原子的水化进行了对比,从原子层面探究了煤泥水难沉降脱水的原因。利用分子动力学模拟还可以精确确定矿物表面活性位点,实现药剂的定向吸附。徐龙华等[40]采用分子动力学等方法研究了油酸钠浮选体系锂辉石的表面晶体化学及各向异性。结果表明,铝原子是锂辉石表面与药剂作用的活性位点,锂辉石晶面单位面积断裂键的差异是导致锂辉石不同浮选行为的原因之一。
矿物在破碎过程中裸露的表面不同,不同的解理面具有不同的表面能。矿物表面结构和电荷的差异,以及表面离子的解离,使得矿物呈现不同的表面性质。经典分子动力学模拟可以量化表面能和解理能数值,并得到与试验相近的结果。Hendrik Heinz等[41]采用经典分子动力学模拟手段,以pcff力场为基础,提出了含有层状硅酸盐原子势能参数的pcff-phyllosilicates力场,用此力场模拟计算了叶腊石、蒙脱石和云母的表面能和解理能,直观展示了三种层状硅酸盐的晶体结构、表面能等,计算得到的晶体参数和表面能数值与试验测量值相比具有较小的误差。矿物表面原子空位是矿物晶体结构中常见的现象,也是造成实际表面与理论解理面存在不同浮选行为的原因之一。Zeinab Naderi Khorshidi等[42]采用分子动力学模拟研究了碱性条件下Al和Si空位对高岭石表面离子溶解的影响,并通过分析缺陷晶体表面,解释溶液中碱金属离子Na+和K+在高岭石表面的离子交换,从而得出了晶格缺陷影响高岭土物化性质的机理。
矿物表面的润湿性决定了浮选过程中矿物的浮选行为,是水分子在矿物表面吸附的直接表征,水分子在表面的作用位点和方式不同,矿物表面水化程度不同。Kaustubh Shrimali[43]采用分子动力学模拟和原子力显微镜,研究了不同pH条件下赤铁矿表面润湿性。结果表明,在碱性条件下,羟基化赤铁矿表面的形成增加了赤铁矿表面的亲水性,羟基化表面与水化表面和疏水表面不同,且疏水表面的水解作用可以使赤铁矿表面亲水,计算结果与原子力显微镜研究结构一致。Dimitrios Argyris等[44]运用经典分子动力学模拟研究了表面羟基化程度不同的石英表面,通过模拟计算水分子在石英表面的作用概率以及均方位移来研究不同表面水的动力学特征。研究表明,表面水的结构和动力学特征的影响因素有固体表面粗糙度、化学组成不均匀性和表面电荷不均匀性;羟基化程度越高,吸附的水层越厚,水分子优先吸附在表面的氧活性位点。
经典分子动力学模拟在矿物晶体结构和表面结构研究中的应用,克服了传统检测的局限,直观展现了矿物解理面的特性,通过量化表面能、表面原子键长和键角等参数,研究表面润湿性。对矿物表面离子溶解和空位、缺陷等的分子动力学研究使得模拟更接近于实际矿物特征,且丰富了矿物晶体化学和矿物表面化学等相关理论。
2.2 矿物与药剂的相互作用矿物浮选的关键是浮选药剂在矿物表面的作用,红外光谱和动电位等常规分析检测手段宏观展示了浮选药剂的作用方式,经典分子动力学模拟从原子或分子相互作用角度诠释了浮选药剂分子在矿物表面活性位点的吸附行为,利用不同药剂在矿物表面的吸附差异和浮选药剂在不同矿物表面的吸附差异,提高浮选的选择性,并深入解释浮选药剂选择性浮选矿物的机理。
药剂在矿物表面的吸附差异是药剂选择性浮选矿物的直接原因,对药剂与矿物相互作用进行分子动力学模拟,可以从吸附能和吸附构型等角度探索药剂的选择性。刘安和樊民强[45]采用经典分子动力学模拟研究了不同溶液条件下十二胺在石英和磁铁矿表面的吸附,通过构建吸附模型和计算相互作用能并结合吸附热力学,从分子力学和热力学层面揭示了浮选过程中十二胺在石英和磁铁矿表面选择性吸附的原因。陈智杰等[46]研究了柠檬酸对油酸钠浮选蓝晶石的调整作用,基于分子动力学分别计算了水与柠檬酸在蓝晶石表面的吸附能,模拟结果表明,柠檬酸与蓝晶石的相互作用强于水在蓝晶石表面的相互作用,因此柠檬酸会排开蓝晶石表面的水分子,吸附在蓝晶石表面的活性位点,并影响油酸钠在表面的吸附。刘建东等[47]利用分子动力学模拟研究了捕收剂CSU-Y在钼酸钙、氟磷灰石以及黄铁矿表面的吸附差异,揭示了浮选过程中CSU-Y对钼酸钙和脉石矿物的浮选差异,解释了捕收剂CSU-Y浮选分离钼酸钙和脉石矿物的机理。李丽匣等[48, 49]采用经典分子动力学模拟研究了油酸钠浮选体系中含碳酸盐铁矿石的浮选差异,从药剂与矿物表面相互作用能、药剂吸附构型等角度解释了含碳酸盐铁矿石中菱铁矿对捕收剂浮选赤铁矿的影响。
浮选药剂在矿物表面常见的作用方式有物理吸附、化学吸附和氢键等,不同的作用方式使得浮选药剂在矿物表面的吸附强度不同,同时,浮选药剂基团在矿物表面的取向决定了矿物在药剂体系的可浮性,经典分子动力学模拟可以通过分析原子间作用距离、原子间电荷转移以及相互作用能等,确定浮选药剂在矿物表面的吸附方式。Beena Rai等[50]研究了油酸和十二胺在锂辉石(001)和(110)面的吸附,油酸和十二胺的作用方式分别为物理吸附和化学吸附,采用经典分子动力学模拟计算矿物-药剂相互作用能,理论计算得到的吸附能变化趋势与试验值相一致。Du等[51]针对糊精和十二烷基三甲基溴化铵(DTAB)在滑石表面的作用进行了分子动力学模拟。研究表明,滑石基面疏水,与水分子作用后不会紧密接触,二者之间存在3 Å的空隙,DTAB和糊精的疏水基团通过疏水作用力优先吸附在基面上;滑石端面Si-O键和Mg-O键断裂,氢键作用的存在使得端面亲水,DTAB通过静电作用吸附在端面,糊精分子在端面的作用比水弱,不能吸附在端面上。浮选药剂性质不同,在矿物表面作用方式不同,通过分析药剂在矿物表面的吸附构型可以得到药剂在矿物表面的作用方式以及作用强弱。Kaustubh Shrimali[52]利用分子动力学模拟直观展示了醚胺和淀粉在石英反浮选体系的作用,分析得出在石英表面形成了类络合物,与试验结果和前期预测结果相一致。
经典分子动力学模拟在矿物与药剂相互作用研究中的应用,加深了对浮选药剂作用的探索,能更好地解释捕收剂、抑制剂和活化剂等在矿物表面作用的选择性。浮选药剂在矿物表面吸附构型直观展示了浮选药剂作用的选择性差异,结合表面能和原子参数变化等量化指标的分析,经典分子动力学模拟在研究矿物与浮选药剂的相互作用机理方面获得了广泛应用。
2.3 药剂筛选和药剂分子设计为了满足矿产资源开发与综合利用的要求,针对浮选药剂的研究已经不仅仅满足于对浮选药剂的筛选,新型高效药剂分子的设计和利用逐渐成为研究热点。通过浮选和分析筛选有效基团,探究基团在矿物表面的作用,并依据基团性质设计新型药剂,实现浮选药剂的靶向作用,最终实现有用矿物的高选择性分选,并降低浮选成本[53]。
经典分子动力学模拟可以通过定向吸附预测浮选药剂分子结构,并通过吸附构型研究不同药剂在矿物表面的吸附差异,有效筛选浮选性能好的单一浮选药剂和具有协同作用的组合浮选药剂。吴桂叶等[54]基于黄铜矿和辉钼矿等硫化矿的晶体结构,通过靶点药物分子设计,预测了黄铜矿抑制剂的分子结构,并构建了巯基乙酸钠在硫化矿物表面的吸附模型,利用UFF力场模拟计算了药剂与矿物表面的相互作用能,在原子层面研究了巯基乙酸钠的选择性抑制,采用经典分子动力学模拟,验证所预测的抑制剂分子结构,并揭示了抑制剂的抑制机理。郭丽娜等[55]基于单矿物浮选试验、动电位和红外光谱分析,结合经典分子动力学模拟,研究了十二胺盐酸盐和十二胺聚氧乙烯醚对煤系高岭石的浮选和作用机理。分子动力学吸附模型表明,十二胺聚氧乙烯醚与高岭石的作用距离小于十二胺盐酸盐与高岭石的作用距离,并且十二胺聚氧乙烯醚具有较大的作用面积和较低的吸附能,理论计算结果与浮选结果相一致。刘臻等[56]采用CLAYFF力场和OPLS力场研究了十二胺、十二醇和胺醇混合药剂在石英表面的吸附,基于稳定吸附模型分析药剂在石英表面的团簇形貌以及水分子分布,十二胺可以形成稳定的柱状半胶束,单独的十二醇并不与石英表面作用,但胺醇混合药剂中的十二醇可以通过疏水作用吸附在十二胺的半胶束上,从而起到调节矿物表面电位的作用,进而提高浮选效率。
浮选药剂的官能团和疏水基团等的性质决定了药剂的捕收、抑制、活化等性能,采用有效的官能团和不同长度的碳链,设计新型浮选药剂,并进行经典分子动力学模拟,针对效果好的浮选药剂进行浮选试验验证,实现浮选药剂的筛选和分子设计。Hendrik Heinz等[57]研究了官能团种类、碳链长度不同的烷基链在层状硅酸盐表面的作用,并对十二种烷基伯胺类表面活性剂进行了经典分子动力学模拟计算,最终得到官能团种类和碳链长度对层状硅酸盐构型、层间密度和层间距离的影响,得到的结果与试验值相吻合。除了可实现对不同碳链长度的药剂进行筛选外,分子动力学还可对新的官能团进行筛选。Hrushikesh Sahoo等[58]采用COMPASS力场研究了新型捕收剂——含醚键烷基季铵阳离子的聚合物离子液体对石英的浮选,考察了碳链长度对浮选性能的影响。研究表明,聚合物离子液体通过静电力和范德华力吸附在石英表面,捕收剂在石英表面的覆盖和吸附能决定了其对石英的捕收性能。Ivan Moncayo-Riascos等[59]基于分子动力学模拟构建的分子模型,研究不同捕收剂对金矿表面润湿性的影响并筛选效果较好的捕收剂。结果表明,碳链与水之间的作用能高于矿物与水之间的作用力是捕收剂提高金矿表面疏水性的主要原因。
基于药剂筛选和药剂分子设计的经典分子动力学模拟,可以大大提高筛选和设计效率,降低成本。可以对具有不同作用基团和不同疏水基的药剂在浮选中的作用进行研究,丰富药剂在矿物表面选择性作用的机理,为浮选药剂的合成提供理论依据。
3 结论综合利用矿物晶体化学、浮选电化学、浮选表面化学和分子模拟等理论,可以有效研究矿物晶体结构和表面结构性质、研究浮选药剂在矿物表面的作用机制,并辅助药剂筛选和药剂分子设计,完善矿物浮选理论。经典分子动力学模拟可以直观展现矿物晶体和表面结构、浮选药剂分子以及药剂在矿物表面的作用方式,通过计算动力学相关性质并统计微观原子性质来解释宏观现象,从原子层面分析分子间相互作用,并保持与实验结果较高的一致性。基于经典分子动力学模拟的浮选研究可以深入分析矿物晶体化学和表面化学,合理解释浮选机理。因此,随着计算机模拟技术的飞速发展,经典分子动力学模拟将成为有效预测和解释浮选现象的重要手段,并促进和加深矿物浮选界面相关性质和反应的研究,通过研究浮选过程中矿物界面反应的动态变化来填补常规检测手段的空白,实现高效和深入的浮选试验研究。
然而,经典分子动力学模拟忽略了电子极化效应,无法用来研究原子之间电荷转移以及成断键相关信息。与此同时,经典分子动力学模拟过分依赖力场,且分子力场的局限性使得力场参数无法直接应用于不同浮选体系。因此,基于经典力场,开发更精确和更具适应性的分子间相互作用势能函数是确保分子动力学模拟在浮选研究中广泛应用的前提。分子动力学模拟在浮选领域的发展有两条途径:其一是优化力场参数,发展具有更高迁移性和更精确的力场;其二是建立新的量子力学力场,将量子力学与经典分子动力学相结合,更好的研究矿物晶体结构和揭示矿物与药剂相互作用。
| [1] |
江建军, 缪灵, 梁培, 等. 计算材料学-设计实践方法[M]. 北京: 高等教育出版社, 2010.
|
| [2] |
Daan Frenkel, Berend Smit, Mark A. Ratner. Understanding molecular simulation:from algorithms to applications[J]. Physics Today, 1997(7): 66. |
| [3] |
Alder B.J., Wainwright T.E.. Phase transition for a hard sphere system[J]. The Journal of Chemical Physics, 1957, 27(5): 1208-1209. DOI:10.1063/1.1743957 |
| [4] |
Jacob D. Durrant, Andrew Mc Cammon J.. Molecular dynamics simulations and drug discovery[J]. BMC Biology, 2011, 9(1): 71. DOI:10.1186/1741-7007-9-71 |
| [5] |
Tao Feng, Mingming Li, Jingjie Zhou, et al. Application of molecular dynamics simulation in food carbohydrate research:a review[J]. Innovative Food Science & Emerging Technologies, 2015, 31: 1-13. |
| [6] |
Martin Karplus, Andrew Mc Cammon J.. Molecular dynamics simulations of biomolecules[J]. Nature Structural Biology, 2002, 9(9): 646-652. DOI:10.1038/nsb0902-646 |
| [7] |
Yuxiu Li, Jinliang Xu, Dongqing Li. Molecular dynamics simulation of nanoscale liquid flows[J]. Microfluidics and Nanofluidics, 2010, 9(6): 1011-1031. DOI:10.1007/s10404-010-0612-5 |
| [8] |
Erik Lindahl, Mark S. P. Sansom. Membrane proteins:molecular dynamics simulations[J]. Current Opinion in Structural Biology, 2008, 18(4): 425-431. DOI:10.1016/j.sbi.2008.02.003 |
| [9] |
贾二广. In-Sn, Ga-Sn和Ge15Te85熔体结构的研究[D]. 合肥: 中国科学院合肥物质科学研究院, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1631857
|
| [10] |
单斌, 陈征征, 陈蓉. 材料学的纳米尺度计算模拟:从基本原理到算法实现[M]. 武汉: 华中科技大学出版社, 2015.
|
| [11] |
李琼光, 聂春红, 张红梅, 等. 分子模拟在分子筛的结构优化及催化领域的研究[J]. 化学工程师, 2017, 31(3): 51-55. |
| [12] |
Martin J. Field. A practical introduction to the simulation of molecular systems:2nd edition[M]. Cambridge: Cambridge University Press, 2007.
|
| [13] |
陈翔, 侯廷政, 彭翃杰, 等. 第一性原理计算在锂硫电池中的应用进展评述[J]. 储能科学与技术, 2017, 6(3): 500-521. DOI:10.12028/j.issn.2095-4239.2017.0031 |
| [14] |
蓝建慧, 卢贵武, 黄乔松, 等. 从头计算分子动力学方法及其应用[J]. 石油大学学报(自然科学版), 2005, 29(4): 143-146. |
| [15] |
胡岳华, 王淀佐. 现代浮选化学研究进展与展望[J]. 中国科学基金, 2001(2): 78-83. |
| [16] |
崔守鑫, 胡海泉, 肖效光, 等. 分子动力学模拟基本原理和主要技术[J]. 聊城大学学报(自然科学版), 2005, 18(1): 30-34. |
| [17] |
申海兰, 赵靖松. 分子动力学模拟方法概述[J]. 装备制造技术, 2007(10): 29-30, 34. DOI:10.3969/j.issn.1672-545X.2007.10.012 |
| [18] |
杨频, 张士国. 分子力学的基本原理[J]. 大学化学, 1990, 5(4): 9-13. DOI:10.3866/PKU.DXHX19900402 |
| [19] |
周晓平, 田壮壮, 忽晓伟. 分子动力学模拟方法概述[J]. 硅谷, 2012(23): 40-41. DOI:10.3969/j.issn.1671-7597.2012.23.050 |
| [20] |
Binder Kurt, Horbach Jürgen, Kob Walter, et al. Molecular dynamics simulations[J]. Journal of Physics:Condensed Matter, 2004, 16(5): S429. DOI:10.1088/0953-8984/16/5/006 |
| [21] |
Hans C. Andersen. Molecular dynamics simulations at constant pressure and/or temperature[J]. The Journal of Chemical Physics, 1980, 72(4): 2384-2393. DOI:10.1063/1.439486 |
| [22] |
高加力. 新一代高精度生物大分子力场[J]. 中国科学基金, 2018(1): 103-106. |
| [23] |
Yunling Liu, Lan Tao, Jianjun Lu, et al. A novel force field parameter optimization method based on LSSVR for ECEPP[J]. FEBS Letters, 2011, 585(6): 888-892. DOI:10.1016/j.febslet.2011.02.019 |
| [24] |
周晓平, 田壮壮, 薛迪杰. 力场在分子动力学模拟中的应用[J]. 科学导报, 2016(9): 280-281. |
| [25] |
Nevena Todorova, Sue Legge F., Herbert Treutlein, et al. Systematic comparison of empirical forcefields for molecular dynamic simulation of insulin[J]. The Journal of Physical Chemistry B, 2008, 112(35): 11137-11146. DOI:10.1021/jp076825d |
| [26] |
George A. Khoury, Jeff P. Thompson, James Smadbeck, et al. Forcefield_PTM:Ab initio charge and AMBER forcefield parameters for frequently occurring post-translational modifications[J]. Journal of Chemical Theory and Computation, 2013, 9(12): 5653-5674. DOI:10.1021/ct400556v |
| [27] |
Michael F. Crowley, Mark J. Williamson, Ross C. Walker. CHAMBER:Comprehensive support for CHARMM force fields within the AMBER software[J]. International Journal of Quantum Chemistry, 2009, 109(15): 3767-3772. DOI:10.1002/qua.v109:15 |
| [28] |
Norman L. Allinger, Young H. Yuh, Jenn Huei Lii. Molecular mechanics. the MM3 force field for hydrocarbons. 1[J]. Journal of the American Chemical Society, 1989, 111(23): 8551-8566. DOI:10.1021/ja00205a001 |
| [29] |
Jurgen Lange, Fernando Gomes de Souza junior, Marcio Nele, et al. Molecular dynamic simulation of oxaliplatin diffusion in poly(lactic acid-co-glycolic acid). Part A:parameterization and validation of the force field CVFF[J]. Macromolecular Theory and Simulations, 2016, 25(1): 45-62. DOI:10.1002/mats.v25.1 |
| [30] |
Verma A., Gopal S.M., Schug A., et al. All atom protein folding with free-energy forcefields[J]. Progress in Molecular Biology and Translational Sciences, 2008, 83: 181-253. DOI:10.1016/S0079-6603(08)00605-3 |
| [31] |
Huai Sun, Zhao Jin, Chunwei Yang, et al. COMPASS Ⅱ:extended coverage for polymer and drug-like molecule databases[J]. Journal of Molecular Modeling, 2016, 22(2): 47. DOI:10.1007/s00894-016-2909-0 |
| [32] |
Peter James Dyer. Molecular modeling of aqueous solutions: the effects of molecular polarization on classical forcefield development[D]. Ann Arbor: Vanderbilt University, 2008.
|
| [33] |
Liaoran Cao, Chunyu Zhang, Dinglin Zhang, et al. Recent developments in using molecular dynamics simulation techniques to study biomolecules[J]. Wuli huaxue xuebao, 2017, 33(7): 1354-1365. |
| [34] |
佟志芳, 肖成, 魏战龙. 分子动力学模拟及其在冶金炉渣中的应用研究[J]. 有色金属科学与工程, 2016, 7(3): 15-20. |
| [35] |
陈正隆, 徐为人, 汤立达. 分子模拟的理论与实践[M]. 北京: 化学工业出版社, 2007.
|
| [36] |
Satoru G. Itoh, Hisashi Okumura, Yuko Okamoto. Generalized-ensemble algorithms for molecular dynamics simulations[J]. Molecular Simulation, 2007, 33(1-2): 47-56. DOI:10.1080/08927020601096812 |
| [37] |
Stoneham A.M., Harding J.H.. Computer simulation of interfaces:what do we need to know?[J]. Acta Materialia, 1998, 46(7): 2255-2261. DOI:10.1016/S1359-6454(98)80006-2 |
| [38] |
罗思岗, 王福良. 分子力学在研究浮选药剂与矿物表面作用中的应用[J]. 矿冶, 2009, 18(1): 1-4. |
| [39] |
闵凡飞, 陈军, 彭陈亮. 煤泥水中微细高岭石/蒙脱石颗粒表面水化分子动力学模拟研究[J]. 煤炭学报, 2018, 43(1): 242-249. |
| [40] |
徐龙华, 田佳, 董发勤, 等. 油酸钠浮选锂辉石的表面晶体化学及各向异性[J]. 中国有色金属学报, 2016, 26(10): 2214-2221. |
| [41] |
Hendrik Heinz, Hilmar Koerner, Kelly L. Anderson, et al. Force field for mica-type silicates and dynamics of octadecylammonium chains grafted to montmorillonite[J]. Chemistry of Materials, 2005, 17(23): 5658-5669. DOI:10.1021/cm0509328 |
| [42] |
Zeinab Naderi Khorshid, Xiaoli Tan, Qi Liu, et al. Influence of structural Al and Si vacancies on the interaction of kaolinite basal surfaces with alkali cations:a molecular dynamics study[J]. Computational Materials Science, 2017, 140: 267-274. DOI:10.1016/j.commatsci.2017.09.004 |
| [43] |
Kaustubh Shrimali, Jiaqi Jin, Behzad Vaziri Hassas, et al. The surface state of hematite and its wetting characteristics[J]. Journal of Colloid and Interface Science, 2016, 477: 16-24. DOI:10.1016/j.jcis.2016.05.030 |
| [44] |
Dimitrios Argyris, David R. Cole, Alberto Striolo. Dynamic behavior of interfacial water at the silica surface[J]. The Journal of Physical Chemistry C, 2009, 113(45): 19591-19600. DOI:10.1021/jp906150n |
| [45] |
刘安, 樊民强. 水相环境中十二胺在石英及磁铁矿表面吸附的分子动力学模拟[J]. 中国有色金属学报, 2015, 25(8): 2226-2235. |
| [46] |
陈智杰, 高惠民, 任子杰, 等. 柠檬酸对蓝晶石浮选行为的影响研究[J]. 中国矿业, 2016, 25(7): 125-129. |
| [47] |
刘建东, 王振, 刘润清, 等. 捕收剂CSU-Y在钼酸钙表面的吸附机理研究[J]. 矿冶工程, 2015, 35(5): 42-45. |
| [48] |
Lixia Li, Haiqing Hao, Zhitao Yuan, et al. Molecular dynamics simulation of siderite-hematite-quartz flotation with sodium oleate[J]. Applied Surface Science, 2017, 419: 557-563. DOI:10.1016/j.apsusc.2017.05.069 |
| [49] |
Haiqing Hao, Lixia Li, Zhitao Yuan, et al. Molecular arrangement of starch, Ca2+ and oleate ions in the siderite-hematite-quartz flotation system[J]. Journal of Molecular Liquids, 2018, 254: 349-356. DOI:10.1016/j.molliq.2018.01.117 |
| [50] |
Beena Rai, Sathish P., Jyotsna Tanwar, et al. A molecular dynamics study of the interaction of oleate and dodecylammonium chloride surfactants with complex aluminosilicate minerals[J]. Journal of Colloid and Interface Science, 2011, 362(2): 510-516. DOI:10.1016/j.jcis.2011.06.069 |
| [51] |
Hao Du, Miller J.D.. A molecular dynamics simulation study of water structure and adsorption states at talc surfaces[J]. International Journal of Mineral Processing, 2007, 84(1): 172-184. |
| [52] |
Kaustubh Shrimali, Xihui Yin, Xuming Wang, et al. Fundamental issues on the influence of starch in amine adsorption by quartz[J]. Colloids and Surfaces A:Physicochemical and Engineering Aspects, 2017, 522: 642-651. DOI:10.1016/j.colsurfa.2017.03.031 |
| [53] |
张行荣, 刘龙利, 吴桂叶, 等. 浮选药剂分子结构设计原理概述[J]. 矿冶, 2013, 22(3): 25-29. |
| [54] |
吴桂叶, 刘龙利, 张行荣, 等. 计算机辅助研究黄铜矿抑制剂的分子结构特征[J]. 有色金属(选矿部分), 2013(S1): 268-271, 274. |
| [55] |
郭丽娜, 李志红, 朱张磊, 等. 阳离子捕收剂对高岭石的捕收性能及动力学模拟[J]. 中国矿业, 2017, 26(5): 112-116, 121. |
| [56] |
刘臻, 孙泽, 于建国. 醇胺药剂与石英界面作用的分子动力学模拟[J]. 华东理工大学学报(自然科学版), 2015, 41(1): 9-14. |
| [57] |
Hendrik Heinz, Vaia R.A., Farmer B.L.. Relation between packing density and thermal transitions of alkyl chains on layered silicate and metal surfaces[J]. Langmuir, 2008, 24(8): 3727-3733. DOI:10.1021/la703019e |
| [58] |
Hrushikesh Sahoo, Nishant Sinha, Swagat S. Rath, et al. Ionic liquids as novel quartz collectors:insights from experiments and theory[J]. Chemical Engineering Journal, 2015, 273: 46-54. DOI:10.1016/j.cej.2015.03.050 |
| [59] |
Ivan Moncayo-Riascos, Bibian A. Hoyos. Effect of collector molecular structure on the wettability of gold for froth flotation[J]. Applied Surface Science, 2017, 420: 691-699. DOI:10.1016/j.apsusc.2017.05.197 |
 2018
2018 

 ,
张晨,
袁致涛
,
张晨,
袁致涛