| 氨浸络合罐体出入口结构对络合浓度的影响研究 |
我国有色金属、黄金产量均居世界第一,但我国铜矿产资源严重短缺,铜矿的人均拥有量仅为世界平均水平的13%。随着我国经济的高速发展,金属矿产资源供需矛盾日益突出[1-2]。
氨浸法是目前在有色金属湿法冶金中应用比较广泛的一种方法,以氨及氨加铵盐做浸出剂的浸出过程称之为氨浸,氨浸法的优越性在于能有选择性的浸出可与氨发生络合反应的金属离子,而与常见的铁、硅、铝、钙等杂质不发生反应,浸出液非常纯净,便于下一步的萃取提纯。但是目前氨浸工艺由于其本身工艺特点导致矿石中的金属离子无法充分浸取,氨水无法充分参与反应,导致资源的浪费。本文利用化学反应和多孔介质理论,研究了在反应温度、压强、颗粒粒度、初始氨水浓度不变的情况下,以氧化铜矿为例分析了氨浸罐不同出入口位置对铜氨络合物浓度的影响,以实现氨与氧化铜的高效络合反应。
1 氧化铜的氨浸络合工艺铜氨络合反应是利用氨与氧化铜矿石颗粒中的铜离子发生络合反应,生成化学性质相对稳定的氨配离子,从而将铜离子从氧化铜矿中与其他杂质或其他金属等分离[3],得到含有大量四氨合铜络离子的氨浸溶液,然后根据氨浸液中四氨合铜络离子的特性,选择合适的萃取剂或者其他物理、化学方法将金属铜从氨浸液中提出,得到单质铜的一种湿法冶金方法。目前已知的可以和氨发生络合反应的金属有银、铜、锌、镍、钴、镉、汞等。
氨水溶液在氨浸罐中与氧化铜发生铜氨络合反应,铜与铵根离子结合形成氨配离子,从而将铜从固体矿石中提出,氧化铜矿在氨水中溶解的机理为:
| $ {\rm{CuO + 4N}}{{\rm{H}}_{\rm{3}}}{\rm{ + }}{{\rm{H}}_{\rm{2}}}{\rm{O = Cu(N}}{{\rm{H}}_{\rm{3}}}{{\rm{)}}_{\rm{4}}}{\left( {{\rm{OH}}} \right)_{\rm{2}}} $ | (1) |
得到含有铜的铜氨络合物溶液后,目前较为广泛的提取方法有四种[3]:(1)加热分解法:直接加热铜氨络合物溶液,但该方法在加热过程中会产生大量的氨气,工作条件较差;(2)置换沉积法:利用负电位的金属做还原剂,得到单质铜;(3)溶剂萃取法:使用萃取剂将铜离子从铜氨络合物溶液中萃取出,然后再通过其他的方法获得单质铜;(4)气体还原法:利用H2和SO2等还原性气体的还原性还原金属铜。
氧化铜矿的氨浸过程实质上是氧化铜矿石颗粒中有用的成分被氨水溶解带走,然后再回收浸出液提取铜的一种过程。溶解过程主要有两个层面:第一个层面是氨水与氧化铜矿石颗粒发生化学反应;第二个层面是氨水在氧化铜矿石颗粒中的渗透流动。这两个层面的效果将直接决定氨浸络合结果的好与坏。
难选矿石采用常规的浮选方法很难获得很好的选别指标,而且选矿成本比较高。对这些矿石采用浸出工艺进行处理已成为一种趋势。方建军等在实验室采用搅拌浸出的方法研究了云南东川汤丹难处理氧化铜矿石常温常压氨浸的影响因素,余斌等针对武山低品位氧化铜矿石,从矿石溶浸化学、浸出动力学、工程流体力学和布液参数优化等多个方面进行了系统的研究,根据已有的研究,目前已知的影响铜氨络合反应的因素主要有矿石的粒度、氨水的摩尔浓度和固液比,以及进行络合反应时的温度和压强等[4-7],目前尚未发现有文献研究氨浸罐入口的分布对整个铜氨络合反应过程的影响。传统的氨浸罐入口大多在罐体中部,因改变入口的位置将会直接影响液体在罐体内的分布情况及其与矿物的接触程度,因此本文将重点探讨氨浸罐入口的分布对上述两个层面的具体影响。
2 铜氨络合反应模型 2.1 溶解传输颗粒模型赵阳升[8]等人系统论述了溶解传输的颗粒模型,其代表性的反应符合浸取本征反应的数学表达式:
| $ A\left( {{\rm{aq}}} \right) + bB\left( {\rm{s}} \right) = cC\left( {{\rm{aq}}} \right) + dD\left( {\rm{s}} \right) $ | (2) |
其中A的反应速率为:
| $ {r_A} = \frac{{{\rm{d}}m/{\rm{d}}t}}{{bV}} = {k_s}4{\rm{ \mathsf{ π} }}{r^2}C_{_{\rm{A}}}^{^n} $ |
式中ks—表面反应速率常数,单位为mol/(L·s);r—颗粒半径, 单位为m;b—固体反应物的化学计量数;CA—流体反应物的摩尔浓度,单位为mol/m3;m—固体反应物的摩尔数;V0—反应体积,单位为m3;t—反应时间,单位为s;n—反应级数。
流体反应物通过灰层的阻力较小,同时反应的生成物向外扩散的阻力也较小,随着外层的不断反应,反应速度逐渐变慢,最终会产生一部分未反应核,这是大多数矿物颗粒浸取过程都符合的规律,为了建立收缩核的模型,有下列假设:
(1) 颗粒为球形,且矿石的组分在颗粒内均匀分布;
(2) 反应为不可逆反应;
(3) 流体反应物和反应产物的扩散均服从Fick定律;
(4) 矿石颗粒本身是致密的,基本没有孔隙,反应后变得疏散多孔;
(5) 反应产生的热量几乎忽略不计,认为反应是在等温条件下进行的。
根据上述假设建立一个收缩核模型,模型如图 1所示。图中填充了斜划线的圆表示初始氧化铜颗粒,虚线画圆表示氨水包裹颗粒形成的流体膜,点状线填充的部分表示反应产物或者灰层。
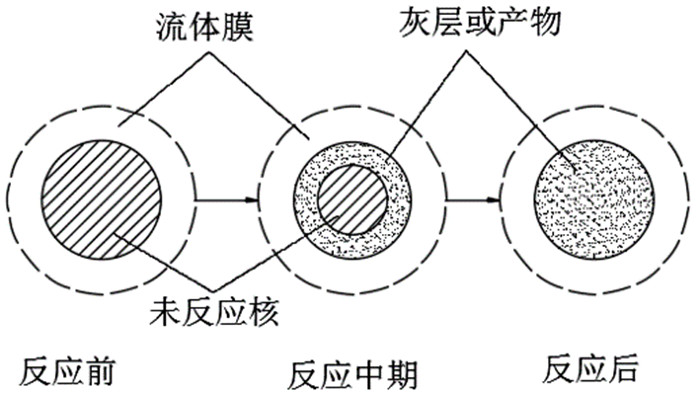 |
| 图 1 未反应收缩核模型 Fig.1 Unreacted shrinkage core model |
2.2 氨水在多孔介质中渗流反应模型
假设氨浸罐内部充满均匀大小的颗粒或块状氧化铜矿,填充物形成了大量的孔隙,氨水溶液在缝隙中流动并与矿物发生化学反应,溶液以渗流的方式进入颗粒内部,与矿石中的铜发生化学反应,生成铜氨络合物溶液,并通过分子扩散的方式迁移到颗粒表层,通过对流扩散到氨浸罐的底部,并通过氨浸罐的出口排除。氨浸罐中的反应模型如图 2所示。
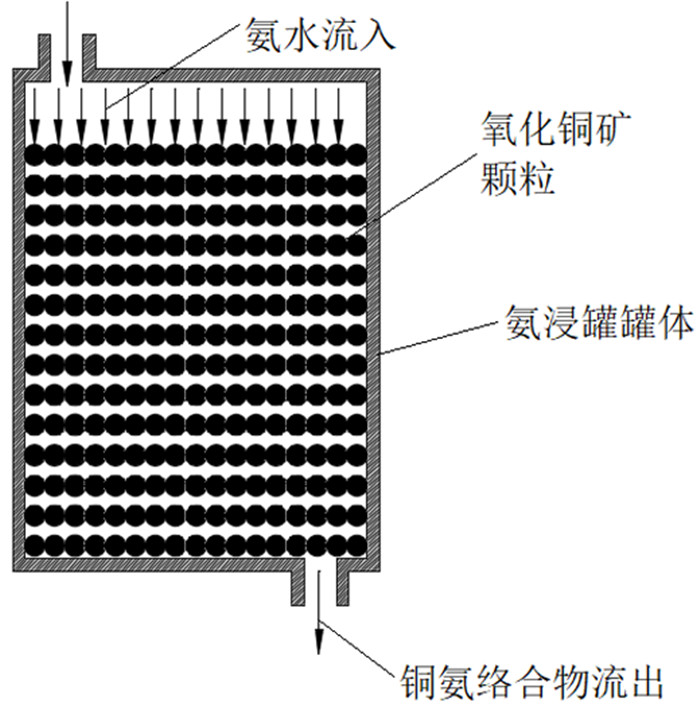 |
| 图 2 氨浸罐液固反应模型 Fig.2 Liquid-solid reaction model of ammonia leaching tank |
不可压缩流体的溶剂传输的渗流方程(不考虑固体骨架的变形):
| $ n\frac{{\partial \rho A}}{{\partial t}} + div\left( {{\rho _A}{V_A}} \right) = {I_A} $ | (3) |
溶剂流体的密度是溶剂与扩散的函数,也是压力的函数:
| $ \begin{array}{l} \rho = {C_A}{\rho _A} + {C_l}{\rho _l}\\ \rho = n\beta p, {V_A} = - k\frac{{\partial p}}{{\partial x}} \end{array} $ | (4) |
将上式带入式(3),可得流体在氧化铜矿中的流动方程:
| $ S\frac{{\partial p}}{{\partial t}} + \rho \left( {\frac{{{\partial ^2}p}}{{\partial {x^2}}} + \frac{{{\partial ^2}p}}{{\partial {y^2}}} + \frac{{{\partial ^2}p}}{{\partial {s^2}}}} \right) = {I_A} $ | (5) |
式中:ρ—流体密度,单位是kg/m3;n—孔隙率,量纲为1;β—流体压缩系数,单位为Pa-1;p—孔隙压力,单位为Pa;S—饱和度,量纲为1,IA—流体的线性动量,单位为kg·m/s。
3 数值计算模型与方法 3.1 COMSOL MultiphysicCOMSOL Multiphysics是一款通用的工程仿真软件平台,Multiphysics翻译为多物理场,因此这个软件的优势就在于多物理场耦合方面。多物理场的本质就是偏微分方程组(PDEs),所以只要是可以用偏微分方程组描述的物理现像,COMSOL Multiphysics都能够很好的计算、模拟、仿真。COMSOL Multiphysics是以有限元法为基础,通过求解偏微分方程(单场)或偏微分方程组(多场)来实现真实物理现象的仿真,被当今世界科学家称为“第一款真正的任意多物理场直接耦合分析软件”。用数学方法求解真实世界的物理现象,COMSOL Multiphysics以高效的计算性能和杰出的多场双向直接耦合分析能力实现了高度精确的数值仿真。目前已经在化学反应、弥散、流体动力学、多孔介质等领域得到了广泛的应用。
3.2 氨浸罐出入口模型氨浸罐的模型有很多种,论文主要从出入口的形式上考虑,考察不同位置的出入口对氨浸反应生成物浓度、流速和压强的影响。氨浸罐流入流出的模型如图 3所示。氨水由入口流入,出口流出。
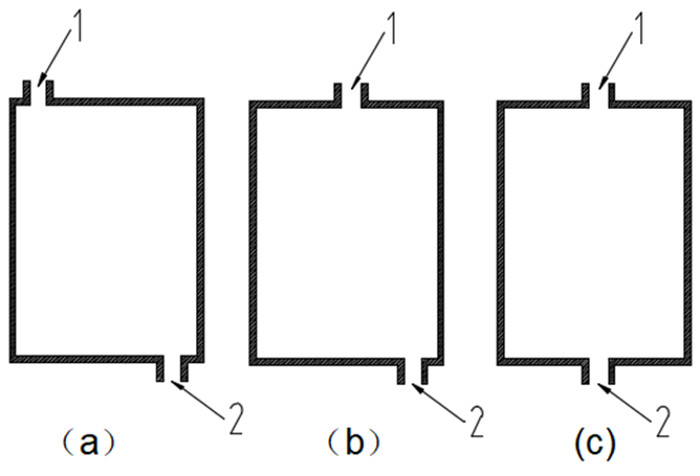 |
| 1:氨水入口; 2:铜氨络合物出口 图 3 氨浸罐出入口位置分析模型 Fig.3 Analysis model of inlet and outlet position of ammonia leaching tank |
图 3(a)入口在左上角,出口在右下角,(b)入口在中间,出口在右下角,(c)出入口均在中间。罐体尺寸:直径D=500 mm,高度H=800 mm;出入均为圆柱形且直径为32 mm,高度为50 mm。
3.3 边界条件在COMSOL Multiphysics中加载Brinkman方程求解,整个罐体作为研究域,方程形式研究控制,假设方程为:
| $ \begin{array}{c} 0 = \nabla \left[ { - pl + \mu \frac{1}{{{\varepsilon _p}}}(\nabla u + {{\left( {\nabla u} \right)}^T}} \right] - \\ \left( {\mu {k^{ - 1}} + {\beta _F}\left| u \right| + \frac{{{Q_{br}}}}{{\varepsilon _{_p}^{^3}}}} \right)u + F + \rho g\\ \rho \nabla \cdot\left( u \right) = {Q_{br}} \end{array} $ | (6) |
流体认为是不可压缩流体,忽略惯性项,将罐体内的氧化铜矿石认为是由若干细微颗粒组成的多孔介质,在Brinkman方程模块的物理模型中选择包含重力、启用多孔介质域,在重力选项中设置重力加速度为y=-9.8 m/s2,参考压力水平p为1个大气压,温度T为293.15 K。氨水密度为900 kg/cm3, 动力粘度μ为1.14×109 Pa·s,多孔介质孔隙率εp为0.7,渗透率κ为1e-12 m2,介质为各向同性,初始速度场u(x)为1 m/s,u(y)为0。
3.4 化学模块与多孔介质稀物质传递在COMSOL Multiphysics的化学模块中,将化学反应方程式设置为A(ads)+B+C=D,其中A为CuO,B为NH4,C为H2O,D为反应生成物。反应类型设置为不可逆反应,反应速率设置为自动,正反应速率常数kf为0.015 m6/(s·mol2),反应活化能为12.3 kJ/mol,反应焓、反应熵、反应热源均设置为自动,域选择选择氨浸罐的罐体,并指定氨浸罐中各个反应物的参数,其中CuO的摩尔质量为0.08 kg/mol,NH4的摩尔质量为0.017 kg/mol,水的摩尔质量为0.018 kg/mol,铜氨络合物的摩尔质量为0.114 5 kg/mol,注入氨水浓度为5 000 mol/m3。
多孔介质稀物质传递(tds)模块中,传递机理选择对流和多孔介质的质量传递,流体扩散系数设置为10-9 m2/s,有效扩散系数模型选择Bruggeman模型,在多物理场模块中选择流动耦合,耦合接口源选择Brinkman方程,目标选择多孔介质稀物质传递(tds)。
网格设置中使用物理场控制网格,因为模型不是特别复杂,所以单元尺寸选择较细化即可;在研究模块中选择研究稳态,相对容差设置为0.001。
4 计算结果和讨论 4.1 氨浸罐内生成物浓度分析图 3所设计的三种出入口分布模型在边界条件相同的情况下,生成物(铜氨络合物)浓度如图 4、图 5、图 6所示。
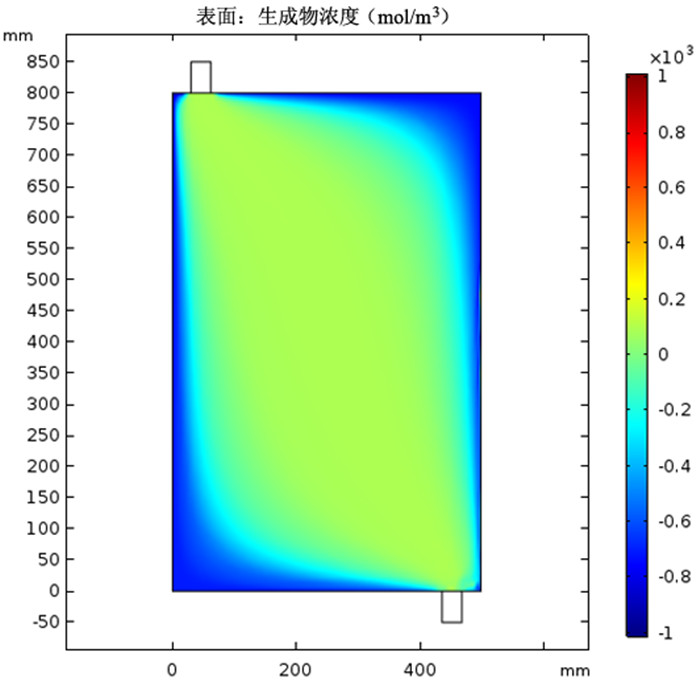 |
| 图 4 采用图 3(a)模型时的铜氨络合物浓度 Fig.4 Concentration of copper ammonia complex when the model in Fig. 3(a) is adopted |
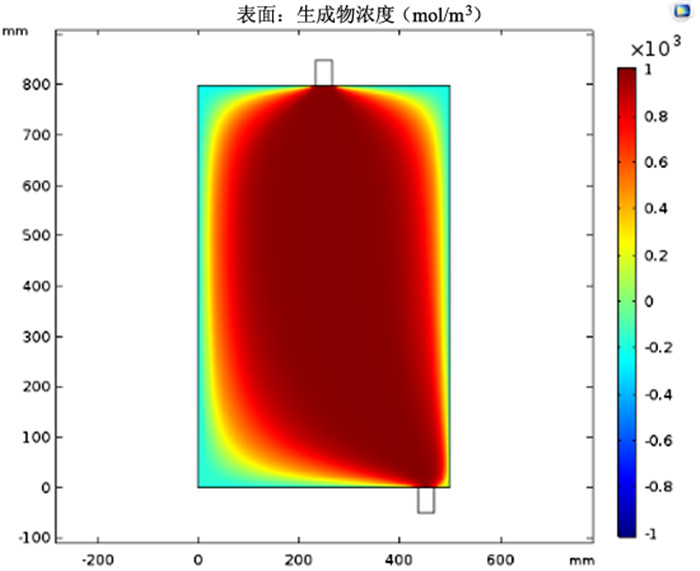 |
| 图 5 采用图 3(b)模型时的铜氨络合物浓度 Fig.5 Concentration of copper ammonium complex when the model in Fig. 3(b) is adopted |
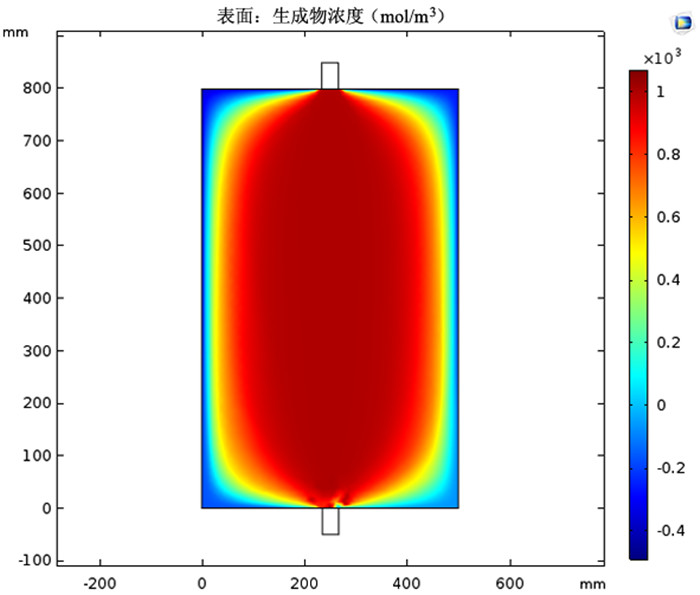 |
| 图 6 采用图 3(c)模型时的铜氨络合物浓度 Fig.6 Concentration of copper-ammonia complex complex when the model in Fig. 3(c) is adopted |
从以上分析可以看出,在矿石粒度、氨水浓度、反应温度以及初始氨水流入速度相同的前提下,图 3(a)模型的铜氨络合物浓度只有200 mol/m3,当采用图 3(b)和图 3(c)的模型时,铜氨络合物的生成浓度大于1 000 mol/m3,比图 3(a)模型的浓度高出5倍,极大地提升了反应的效率和反应的充分程度,此外图 3(b)和图 3(c)相比,图 3(b)无蓝色区域,意味着图 3(b)的反应是三种模型中最充分的,因此我们可以得出这样的结论:出入口的位置对氨浸反应生成的铜氨络合物浓度影响较大,其中入口在氨浸罐顶端的中部,出口在氨浸罐右下角时,铜氨络合物浓度明显增高,反应较为充分,氨浸效果最好。
4.2 氨浸罐出入口模型速度场和压力场分析氨浸罐出入口分布模型采用三种设计,如图(3)所示。图 3(a)入口在左上角,出口在右下角,图 3(b)入口在中间,出口在右下角,图 3(c)出入口均在中间。三种模型分析的速度场和压力场模型如图 7、图 8所示。
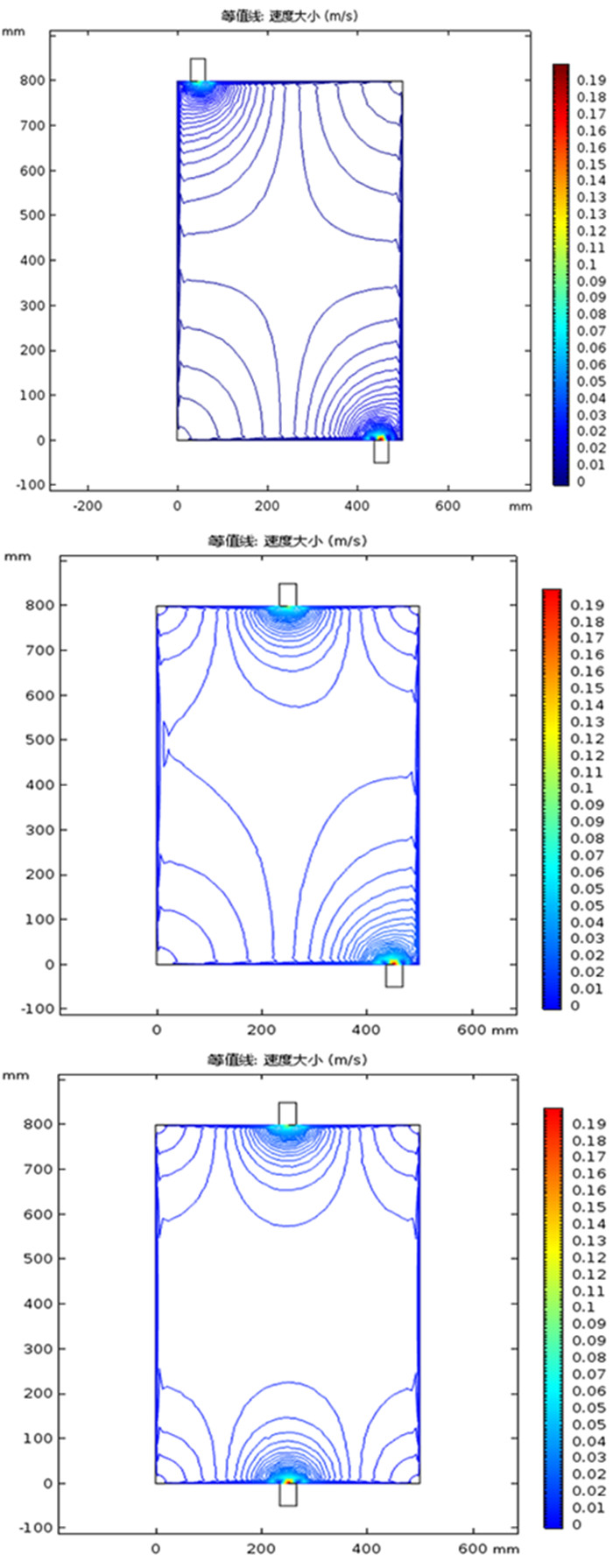 |
| 图 7 氨浸罐流入流出速度等值线 Fig.7 Isoline of inlet and outlet velocity of ammonia leaching tank |
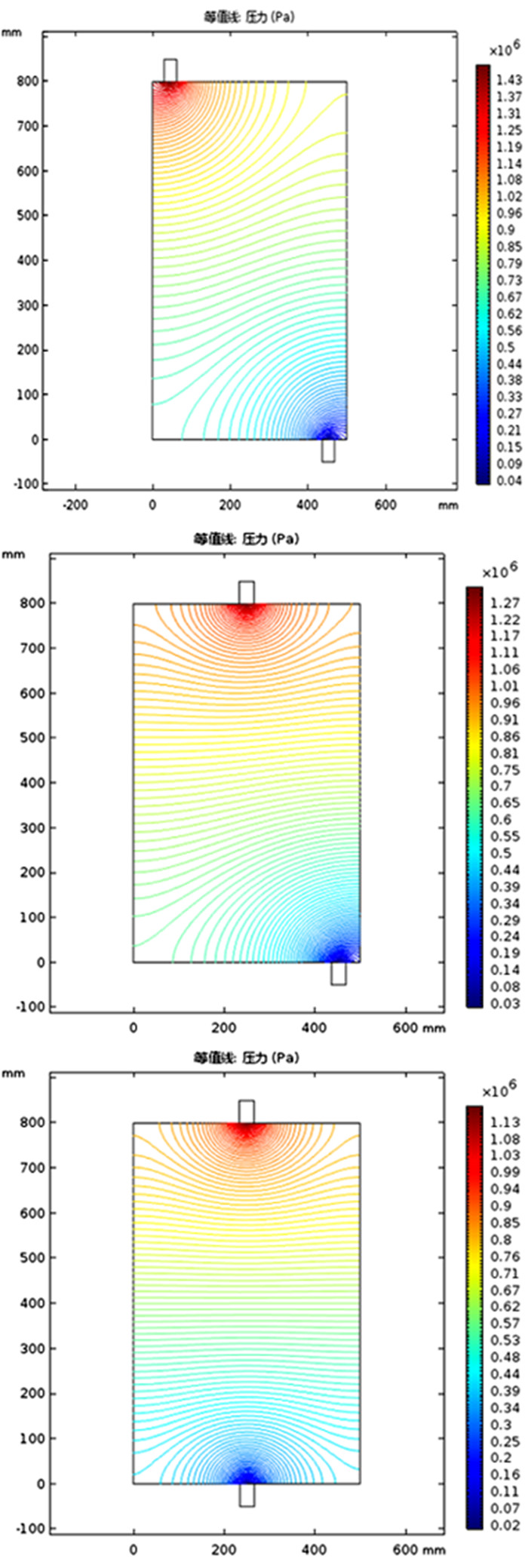 |
| 图 8 氨浸罐内部流体压力等值线 Fig.8 Isoline of fluid pressure of ammonia leaching tank |
从图 7可以看出出入口位置对氨浸罐内液体的流速有一定的影响,图 7(a)的等值线间隙较密集,表明速度波动较大,流速下降最快,壁上流速较高,大量氨水沿着壁面流走,与矿物反应不充分,氨水直接被排出,图 7(b)的等值线间隙比图 7(a)的要大,速度波动较小,图 7(c)等值线密度最大,速度波动最小,且整个罐体内除出入口位置外,速度分布保持较好,氨水沿着整个罐体较均匀下降,可以充分与矿物接触;从图 8可以看出图 8(a)压降最快,初始压强有1.43×106 Pa,但是在罐体的中上部压力衰减到0.7×106 Pa,结合图 7(a)的流速等值线,可以得出造成这种压降的原因是由于氨水从罐体侧壁流失导致的,图 8(b)和图 8(c)中压降均匀,且在罐体的前部分都保持了较高的压力,均大于0.8×106 Pa,可以在罐体中部保持较高的液体压力,便于氨充分和氧化铜矿接触。结合图 7和图 8可以看出,入口在罐体顶部左侧时罐体中部压力衰减较其他两种设计较快,是由于采用该设计时,大量氨水沿着氨浸罐内测的罐体壁向下流失,与罐体中部矿石接触较少所致,最终导致生成的铜氨络合物浓度较低,氨的利用率不高,而将入口移到罐体顶端的中部时,氨水可以较为均匀的由罐体顶部向下渗流,液体在罐体内可以一直保持较高的液体压力,便于液体渗入多孔介质,使得氨与矿石无论在接触面上还是接触时间上,都有了极大的优势,明显图 3(b)与图 3(c)设计比图 3(a)更为合理。
5 结论氨浸罐的出入口设计,对铜氨络合物的生成浓度影响非常显著,所探讨的三种模型从侧面反映了氨浸罐的一些动力学特征:从出入口的位置上看,氨浸罐采用在顶端中间位置放置入口的方式,可以明显的提升铜氨络合物的生成浓度,提升幅度高达5倍,根据仿真结果可以看出图 3(b)将氨浸罐的氨水入口放置在罐体顶端中部,出口放置在罐体底部右下角的设计方式,最为合理,生成的铜氨络合物浓度最高。
尽管氨浸罐有多种设计,工况不尽相同,但对于氨浸罐从生成物效率和节约原材料的方面考虑,所考虑的出入口位置分布对氨浸络合工艺装备的设计仍然具有非常重要的现实意义。
| [1] |
张纪辉.我国金属矿产资源全球化战略研究[D].北京: 中国人民大学, 2005. http://d.wanfangdata.com.cn/Thesis/J0093559
|
| [2] |
孙肇均, 方维萱. 我国有色金属矿山资源现状与新一轮找矿成就[J]. 中国金属通报, 2005, 36: 2-5. |
| [3] |
杨新生. 氨浸过程浅析[J]. 有色金属, 1993(1): 34-37. |
| [4] |
刘志雄.氨性溶液中含铜矿物浸出动力学及氧化铜-锌矿浸出工艺研究[D].长沙: 中南大学, 2012. http://d.wanfangdata.com.cn/Thesis_Y2197996.aspx
|
| [5] |
张铁民, 方建军, 蒋太国, 等. 兰坪燕子洞含银氧化铜矿常温常压氨浸试验研究[J]. 矿产保护与利用, 2014(1): 26-29. |
| [6] |
蒋太国, 方建军, 张铁民, 等. 氧化铜矿选矿技术研究进展[J]. 矿产保护与利用, 2014(2): 49-53. |
| [7] |
方建军, 李艺芬, 鲁相林, 等. 低品位氧化铜矿石常温常压氨浸工艺影响因素研究与工业应用结果[J]. 矿冶工程, 2008, 28(3): 81-83. DOI:10.3969/j.issn.0253-6099.2008.03.021 |
| [8] |
郑永兴, 文书明, 刘健, 等. 难处理氧化铜矿强化浸出的研究概况[J]. 矿产综合利用, 2011(2): 33-36. DOI:10.3969/j.issn.1000-6532.2011.02.010 |
| [9] |
库建刚, 刘殿文, 张文彬. 氧化铜矿氨浸渣的综合回收试验[J]. 中国有色冶金, 2007(4): 30-32. DOI:10.3969/j.issn.1672-6103.2007.04.009 |
| [10] |
赵阳升. 多孔介质多场耦合作用及其工程响应[M]. 北京: 科学出版社, 2010.
|
 2019
2019


 ,
,