| 固阳褐铁矿脱水反应动力学研究 |
2. 内蒙古科技大学 矿业研究院,内蒙古 包头 014010
2. Institute of Mining of Inner Mongolia University of Science and Technology, Baotou 014010, China
随着国内品位高且易选铁矿石资源的日益减少,许多学者对有效开发利用低品位褐铁矿资源进行了大量研究。针对褐铁矿选矿工艺,有单一重力选矿流程、磁化焙烧—磁选和磁选—浮选联合选别流程等[1-5],其中磁化焙烧—弱磁选是应用最为广泛且最为有效的方法。褐铁矿是一种含结晶水的贫氧化铁矿石,在加热的过程中会进行热分解发生脱水反应,对其在磁化焙烧及烧结生产过程中产生重要的影响[6-7]。脱水反应动力学主要研究脱水过程中矿物的化学反应速率以及影响矿物热分解的条件,探讨矿物的脱水反应机理及动力学特性[8],进而更好地控制磁化焙烧及烧结工艺条件。
目前,针对褐铁矿脱水反应机制的相关研究报道较少,并且由于各地褐铁矿生成条件及矿物组成的差异,文献中报道的动力学参数也各不相同[9-11]。本文采用综合热分析技术,结合X射线衍射技术分析研究了固阳褐铁矿磁化焙烧过程中的脱水反应动力学,并计算了相关动力学参数,探讨了脱水反应机理,为更好地控制磁化焙烧条件及进一步的工艺开发和技术研究提供理论依据。
1 试验 1.1 试验原料试验原料取自内蒙古固阳地区,其化学成分和物相分析见表 1和表 2,图 1是原矿的XRD图谱。使用制样机将褐铁矿全部磨至0.074 mm以下,放入干燥箱中加热至110 ℃烘干12 h,去除其中的游离水。
| 表 1 原矿多元素分析结果 /% Table 1 Chemical multi-element analysis of the raw ore |
 |
| 表 2 原矿铁物相的分析结果 /% Table 2 Analytic results of iron phase of the raw ore |
 |
 |
| 图 1 原矿XRD图谱 Fig.1 XRD pattern of the raw ore |
从表 1和表 2中的数据以及图 1可以看出,固阳褐铁矿铁品位较低,脉石矿物主要是石英,主要铁物相为含结晶水的赤褐铁,其分布率达到96.12%。
1.2 试验方法采用德国NETZSCH公司的STA-2500型热重分析仪对样品质量及热量的变化进行测定,试样质量为11 mg,在氮气气氛下,设定载气流量为20 mL/min,升温速率为10 ℃/min,升温区间为40~500 ℃,试验数据由计算机输出。采用丹东通达科技公司的TD 3500型X射线衍射仪对样品进行物相检测,使用Co靶,波长为1.79 Å,扫描范围为10°~80°,使用Jade软件进行物相分析。
1.3 动力学计算方法首先,根据热重分析仪测定的质量损失(TG)曲线计算出反应各温度下的转化率α:
| $ \alpha = \left( {{m_0}-m} \right)/\left( {{m_0}-{m_\infty }} \right) $ | (1) |
式中:m0为起始质量, g;m为某时刻的质量, g;m∞为最终质量, g。
对于任意一个化学反应,其积分式的动力学方程可以表示为:
| $ G\left( \alpha \right) = Kt $ | (2) |
结合Arrhenius提出的速率常数—温度关系式:
| $ K = A\exp \left( {-E/RT} \right) $ | (3) |
可得出关于转化率的积分方程:
| $ \begin{array}{l} \;\;G\left( \alpha \right) = \int {{\rm{d}}\alpha {\rm{/}}f\left( \alpha \right)} = \\ \left( {A/\beta } \right)\int {\exp \left( {-E/RT} \right){\rm{d}}T} \end{array} $ | (4) |
式中:T为反应温度;β为升温速率;A为指前因子;E为活化能;R为普适气体常数(8.314 5 J·mol-1·K-1);f(α)、G(α)为反应的机理函数。
热分析动力学的数据处理方法有很多种,常见的积分求解法有Phadnis法、Zsako法、Coats-Redfern法和Flynn-Wall-Ozawa法[10]。本文采用常用的Coats-Redfern积分法,设f(α)=(1-α)n,得出:
| $ \ln \left[{G\left( \alpha \right)/{T^2}} \right] = \ln \left( {AR/\beta E} \right) -E/RT $ | (5) |
表 3是不同化学反应机制的动力学机理函数[11]。将不同机理函数的G(α)和各温度下的转化率α代入公式(5),建立ln[G(α)/T2]与1/T的直线关系,使用origin软件进行最小二乘法线性拟合,线性相关性系数最大的即为该反应的最概然机理函数,然后通过拟合直线的斜率(-E/R)和截距(ln(AR/βE))即可求出该反应的动力学参数:活化能E和指前因子A。
| 表 3 不同化学反应机制的动力学机理模型 Table 3 Dynamics model of different chemical reaction mechanisms |
 |
2 试验结果与分析 2.1 褐铁矿热分析结果
图 2是褐铁矿脱水反应的TG-DTA曲线,由图 2的失重(TG)曲线结合式(1)可计算出质量转化率α及质量转化速率dα/dt随温度的变化关系,如图 3所示。
 |
| 图 2 褐铁矿的TG-DTA曲线 Fig.2 The TG-DTA profile of limonite |
 |
| 图 3 褐铁矿质量转化率与转化速率与温度的关系 Fig.3 Effect of mass conversion degree and rate as a function of temperature |
从图 2和图 3中可以看出,固阳褐铁矿升温过程中,在248.6 ℃和422.3 ℃时出现了两个明显的吸热峰,表明该反应为吸热反应。从图中可以明显观察到2处质量损失台阶,因此,其脱水过程具体可分为两个反应阶段:第一阶段区间为140~320 ℃,失重率为4.78%,在248.6 ℃时,质量损失速率最快;第二阶段区间为320~465 ℃,失重率为3.84%,在422.3 ℃时,质量损失速率最快,但比第一阶段损失速率有所减缓;总的失重率为8.62%,结合表 1原矿的化学元素分析及脱水反应式:
| $ x{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3} \cdot y{{\rm{H}}_2}{\rm{O}} = x{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3} + y{{\rm{H}}_2}{\rm{O}} $ | (6) |
可求得固阳褐铁矿的分子式为2Fe2O3·3H2O。
2.2 褐铁矿脱水的XRD图图 4是褐铁矿脱水反应过程中不同温度下的X射线衍射图谱。
 |
| 图 4 不同温度下的XRD图谱 Fig.4 XRD pattern at different temperature |
从图 4可以看出,当温度达到200 ℃时,样品中各衍射峰没有发生变化,表明在200 ℃以下,没有发生物相转变,继续升温至300 ℃,针铁矿的部分衍射峰(24.7°、42.8°、62.7°)明显减弱,开始出现赤铁矿的衍射峰,表明此阶段针铁矿开始脱羟基向赤铁矿转变,随着温度的继续升高,针铁矿的衍射峰逐渐消失,赤铁矿的衍射峰逐渐增强,在450 ℃时,针铁矿的衍射峰完全消失,表明此时针铁矿脱羟基过程已经完成,褐铁矿脱水反应基本结束,继续升温至500 ℃,赤铁矿的衍射峰不断增强、矿相逐渐变纯。另外,从图 4中可以看出,随着温度的升高,脉石矿物黄钾铁矾的衍射峰也在不断的减弱,黄钾铁矾的分解可能会对褐铁矿脱水反应过程中的热量变化造成一定的影响。
2.3 褐铁矿脱水反应动力学用热重分析法研究褐铁矿脱水反应动力学时,主要是通过TG-DTA曲线确定最合适的反应机理函数,从而根据拟合直线的斜率和截距来计算脱水反应的动力学参数以及反应速率常数[8, 12]。
将两个阶段下不同温度的质量转化率α代入常用的动力学机理函数G(α)中,建立ln[G(α)/T2]与1/T的直线关系,并使用最小二乘法进行线性拟合,各拟合直线的相关性系数R2列于表 4。
| 表 4 不同机理函数拟合直线的相关性系数 Table 4 Correlation coefficients of fitting curve for different mechanism functions |
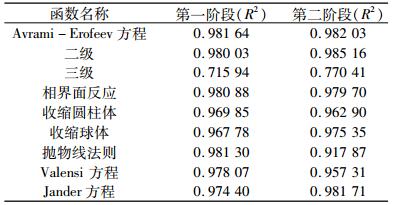 |
从表 4可以看出,固阳褐铁矿脱水反应第一阶段相关性系数最高为0.981 64,反应机理符合Avrami-Erofeev方程,为随机成核和随后生长的一级化学反应,第二阶段相关性系数最高为0.985 16,反应机理符合二级反应函数,为化学反应控制。可能是由于固阳褐铁矿中存在较多的脉石矿物以及图 4 XRD图谱中黄钾铁矾的分解造成各机理函数拟合直线的相关性系数不是很高。
图 5和图 6分别是两个反应阶段相关性系数最高的机理函数的相关性分析曲线。
 |
| 图 5 第一阶段相关性分析曲线 Fig.5 Correlation analysis curves of the first phase |
 |
| 图 6 第二阶段相关性分析曲线 Fig.6 Correlation analysis curves of the second phase |
从图 5和图 6中拟合直线方程的斜率(-E/R)和截距(ln(AR/βE))可求得褐铁矿脱水反应的活化能和指前因子,列于表 5。
| 表 5 褐铁矿脱水反应动力学参数 Table 5 Dehydration Reaction Kinetics parameters of limonite |
 |
由表 5数据可知,褐铁矿脱水反应第一阶段速率常数-温度关系式为K=48.36e-3 432.5/T,第二阶段速率常数-温度关系式为K=1.65×104e-7 746/T,第二阶段的活化能较第一阶段高出33.38 kJ/mol,活化能越大,反应物分子平均能量与活化分子平均能量差值越大,反应越难进行,所需要的能量越高。
3 结论(1) 固阳褐铁矿脱水反应过程分为两个阶段:第一阶段:140~320 ℃,失去结晶水,反应机理符合Avrami-Erofeev方程,为随机成核和随后生长的一级化学反应,第二阶段:320~465 ℃,失去羟基水,反应机理符合二级反应函数,为化学反应控制,第二阶段的反应速率较第一阶段有所减缓。
(2) 固阳褐铁矿脱水反应总的失重率为8.62%,分子式为2Fe2O3·3H2O,采用Coats-Redfern积分法算得第一、第二阶段的反应活化能分别为28.54 kJ/mol、61.92 kJ/mol。
(3) 以后要加强对实际矿石的反应动力学研究,注意脉石矿物对试验结果的影响,结合反应过程的热力学分析,得出更为准确的试验结论。
| [1] |
谢兴中, 王毓华. 褐铁矿选矿研究现状与思考[J]. 金属矿山, 2010, 39(1): 6-10. |
| [2] |
王德英, 孙广周, 赵玉佳. 某地褐铁矿选矿工艺对比研究[J]. 矿产保护与利用, 2012(6): 20-24. |
| [3] |
崔强, 肖婉琴, 郑桂兵, 等. 国外某褐铁矿石磁化焙烧-磨矿-弱磁选试验[J]. 金属矿山, 2016, 45(12): 48-50. DOI:10.3969/j.issn.1001-1250.2016.12.011 |
| [4] |
李俊宁, 袁启东, 陈洲. 某微细粒赤褐铁矿选矿试验研究[J]. 矿产保护与利用, 2014(6): 19-24. |
| [5] |
Peng N, Peng B, Chai L Y, et al. Recovery of iron from zinc calcines by reduction roasting and mag netic separation[J]. Minerals Engineering, 2012, 35(8): 57-60. |
| [6] |
陈伟鹏, 李光卫, 赵增武, 等. 用煤泥作还原剂制备褐铁矿含碳球团[J]. 烧结球团, 2016, 41(5): 38-42. |
| [7] |
黄伟青, 张旭孝, 刘燕霞, 等. 褐铁矿在烧结中的高效使用技术[J]. 钢铁研究学报, 2016, 28(7): 13-19. |
| [8] |
周政, 李艳军, 陈炳炎, 等. 铁矿石焙烧动力学研究现状及发展[J]. 金属矿山, 2015, 44(8): 100-105. |
| [9] |
张翔宇, 李家林, 刘小银. 某褐铁矿脱水反应动力学的研究[J]. 金属材料与冶金工程, 2010, 38(4): 10-13. |
| [10] |
韩磊, 李解, 李保卫, 等. 微波加热褐铁矿的脱水反应动力学[J]. 过程工程学报, 2014, 14(2): 286-290. |
| [11] |
李金莲, 刘万山, 李艳茹, 等. 热分析技术在褐铁矿结晶水热分解中应用研究[J]. 钢铁, 2011, 46(5): 19-22. |
| [12] |
朱志昂, 阮文娟. 物理化学[M]. 北京: 科学出版社, 2014.
|
 2017
2017 
