| 细粒石英的相对润湿性及其浮选行为研究 |
固体颗粒表面的润湿性及其调节是浮选的核心问题。在实践中通常用接触角来表征固体表面润湿性的强弱。通过测定接触角,就可以对颗粒的润湿性和可浮性做出大致的评价[1]。
根据接触角测试原理[2]的不同,可将其分为Wilhemly板法、静止或固定液滴法、斜板法、毛细管上升法以及气泡捕收法;根据三相(气态、液态、固态)接触线不同的移动速率,可将其分为静态接触角法[3-5]和动态接触角法;根据测量物理量的差别,亦可将其分为长度法、量角法、透过法和测力法[6-8]。
块状物料的接触角可以通过光学法、Wilhelmy法等成熟方法获得[9-11],但对粉体物料接触角的测定,目前尚无公认的标准方法,可采用的两种测定方法为压片法和渗透法。压片法是将待测粉体压制成片,然后应用块状接触角的方法进行测定[12-13],由于在试验操作中很难将粉末样品压成表面非常光滑的片状,且也很难确定三相接触点,导致测试结果并不稳定,因此采用压片法测定粉体接触角具有很大的局限性。
然而,浮选体系中的矿物颗粒大小为微米级,属于典型的粉体,矿物颗粒表面润湿性与其可浮性息息相关,准确测定浮选体系中矿物颗粒的表面性质的变化具有重要意义。渗透法是目前测定粉体接触角的主要方法[14-16],测量时先将待测粉体装在内径均匀的空心管中压实,然后通过测定液体在粉体柱中的渗透高度曲线求得接触角。若想计算得到绝对接触角,必须找到对粉末润湿性最好的液体作为基准(此时接触角为0),然而在实际生产和科研中,往往很难找到使粉末完全润湿的液体,因此可以采用这种方法比较不同条件下的相对接触角,从而对试验效果进行对比分析,这无疑对研究工作极富意义。
本文采用Washburn渗透动态法测定粉末的接触角,渗透法测量粉体接触角应用的原理是液体在时间t内上升的高度h,根据Washburn方程[17]有式(1):
| $ {h^2} = \frac{{\left( {CR} \right)\gamma \cos \theta }}{{2\eta }}t $ | (1) |
式中:C-毛细管因子;
R-粉体柱的有效毛细管半径,m;
γ-液体的表面张力,N/m;
η-液体的黏度,Pa·s。
粉体的堆积密度恒定时,CR为定值,可将其视为仪器常数。
当固体粉末均匀填入管中,并将粉体床夯实。管的一端封闭一端垂直插入液体时,由于液体的渗透作用,使得管内的压力变大,由此就会产生压力差,此时Washburn方程可表示为:
| $ K = \beta \gamma \cos \theta /\eta $ | (2) |
所以式
渗透法因其可获得粉体或沉积物的相对接触角,也能客观准确地表征颗粒表面性质而受到重视,在涂料、表面改性、医药、纤维等各方面都有广泛的应用前景。然而用其表征矿物颗粒表面润湿性及相应浮选行为的研究还不够深入[18-19]。
本文系统测定了油酸钠浮选体系中石英在不同条件下的相对接触角,更直观地考察了不同条件下石英表面润湿性的变化规律及其浮选行为特征,在此基础上计算了基于相对接触角的颗粒与气泡黏着前后自由能的变化值,从热力学角度解释了不同条件下的石英表面性质的差异及其对浮选效果的影响。
1 试验材料与方法 1.1 试样及药剂试验使用的石英样品取自鞍钢集团齐大山铁矿选厂,首先采用颚式破碎机将之破碎到-2 mm,再经陶瓷球磨机磨至-0.1 mm。对磨矿产品进行脱水后,再用5%的盐酸溶液按液固比3: 1酸浸3次,每次均连续浸泡24 h,最后用蒸馏水洗涤至中性,可得石英单矿物。样品的元素分析和X射线衍射测试结果分别如表 1和图 1所示。可以看出,石英样品SiO2含量为99%以上,符合单矿物分选试验要求。
| 表 1 石英样品元素分析 /% Table 1 Elemental analysis of quartz |
 |
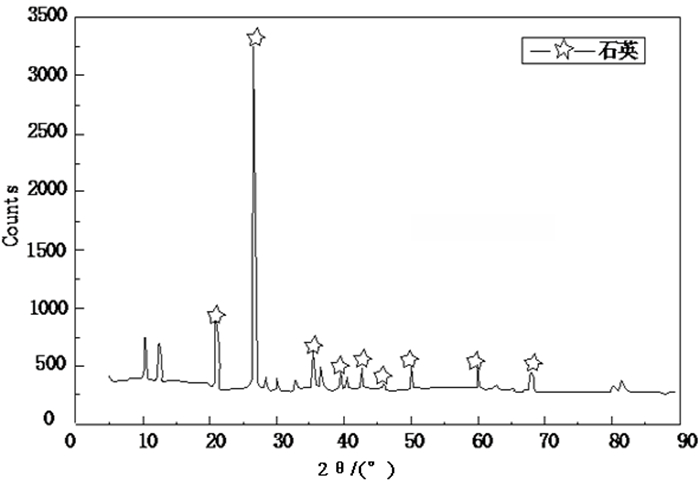 |
| 图 1 石英样品的XRD图谱分析 Fig.1 XRD analysis of quartz |
对于制得的石英样品,进一步通过筛分获得-0.045+0.037 mm粒级矿样,用于单矿物浮选以及相对接触角的测定。
试验所用试剂为配置好的不同pH的氢氧化钠溶液,氢氧化钠和氯化钙均为分析纯,油酸钠为化学纯。
1.2 试验方法 1.2.1 石英浮选试验单矿物浮选试验在50 g XFGCⅡ实验室用挂槽浮选机中进行,每次称取矿样5 g,放入浮选槽中,加入水温为35 ℃的氢氧化钠溶液至35 mL,调整浮选机的搅拌速度为1 320 r/min,依次加入氯化钙、油酸钠溶液,每次加入药剂后均搅拌2 min,浮选时间为4 min,泡沫产品经烘干和称重后计算回收率。
1.2.2 接触角的测定本研究采用的粉体接触角测量仪带有粉体柱制备装置,可以制得紧密程度相近的粉体柱,从而有效避免了因粉体柱性质差异而造成的测量值不稳定的问题。
采取和浮选试验相同的条件对样品进行调浆处理,再将相应的矿浆过滤和烘干,对滤饼进行相对接触角的测量,同时把滤液放置于35 ℃恒温箱中用于表面张力的测定。
相对接触角测试步骤为:首先把2.0 g待测样品装入JF99A型粉体接触角测量仪的石英管中,采用制样机把样品压实后将装有压力传感器的密封头压住石英管;然后将装有去离子水的玻璃器皿置于石英管下方,并使用注射器去除石英管与水接触面的微小气泡,以免影响测试结果;最后打开测试仪器和计算机程序,并点击connect选项使计算机与仪器连接,此时便可读出压差值,每个样品均记录800 s。
1.2.3 表面张力测定表面张力的测定方法为:将置于35 ℃恒温箱中的滤液分别取出,倒入JK99A型全自动张力仪配备的玻璃器皿中;打开仪器,设置相应的参数,将铂金板挂在传感器上,使传感器下降至铂金板全部没在溶液中进行润湿,然后测量滤液的表面张力。
1.2.4 作用前后体系相对自由能的变化计算当颗粒与气泡黏着单位面积时,假定黏着后气泡仍保持球形不变,则颗粒与气泡黏着前后体系自由能变化量[20]为式(3)所述:
| $ - \Delta G = {\gamma _{1 - {\rm{g}}}}\left( {1 - \cos \theta } \right) $ | (3) |
γl-g—液气界面上的表面张力,N/m;
θ—接触角。
γl-g的数值与液体的表面张力相同,带入在不同条件下测得的溶液表面张力值与相对接触角可计算出基于相对接触角的气泡与颗粒黏着单位面积前后体系自由能变化。
2 结果与讨论 2.1 不同pH值时石英表面的相对接触角及浮选行为试验中保持氯化钙和油酸钠的浓度均为25 mmol/L,使用不同的pH值的氢氧化钠溶液,以测得(Δp)2-t关系图如图 2所示。
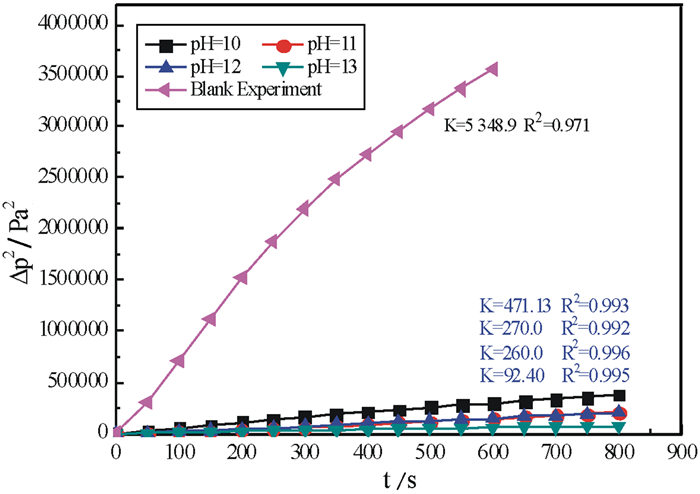 |
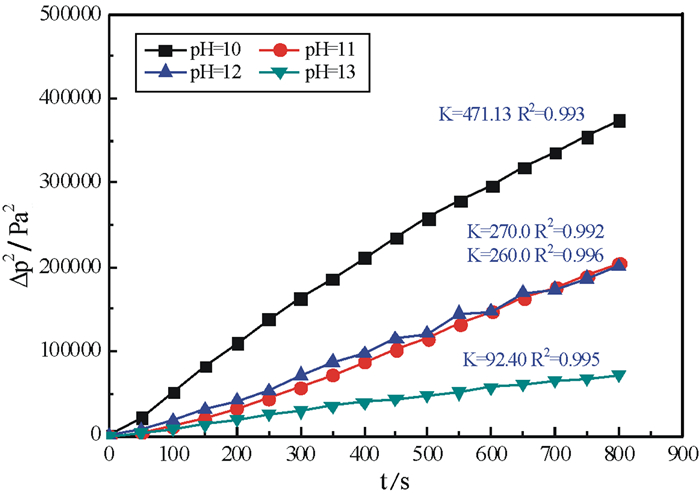
| 图 2 不同pH条件下(Δp)2与时间t的关系曲线图 Fig.2 Relationship between (Δp)2 and t under different pH conditions |
由图 2可以看出,石英所处的溶液pH值越大,压差变化越缓慢,反映出液体对粉体床的渗透速度越慢,即表明在不同的pH条件下,润湿液在粉体床中的渗透速度有着显著的差异:当润湿液的pH值比较小的时候,润湿液对粉体床的渗透作用很快,并且可以看出其与时间有着明显的线性关系;当pH值持续增加时,润湿液对粉体床的润湿速度持续下降,压差的平方与时间成交为明显的线性关系仅体现在350 s之前,之后曲线有小幅度的波动,而且润湿液对粉体床的润湿速度逐渐放缓。由此可知,当活化剂和捕收剂用量比例一定时,通过调整溶液pH值,可以改善他们在石英表面的作用效果,从而使石英表面的疏水性提高。
假定未被药剂处理过的石英表面接触角为0°,结合图 2计算出其他pH值时石英表面相对接触角,同时结合对应药剂条件下单矿物浮选结果,绘制出二者的对比曲线,如图 4所示。
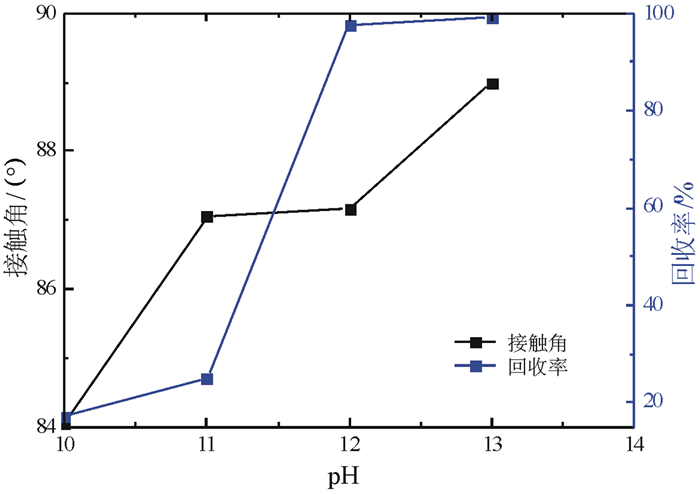 |
| 图 4 不同pH条件下石英相对接触角和回收率 Fig.4 Relative contact angel and quartz recovery under different pH conditions |
由图 4可以看出,不难看出相对接触角和回收率变化规律一致,这就证明了pH会改变石英的表面性质,在很大程度上影响浮选的结果。当矿浆的pH在10~11的范围内,石英的回收率很低。之后,随着pH值的增大,石英的回收率有很大的提高,并且在pH为12的时候达到最大值,再增大pH,回收率稍有降低。但同时也可以看出回收率曲线和接触角的曲线的变化规律重合度并不高,特别是pH=11时,造成这种现象的原因可能是气泡的尺寸不一致,导致气泡升浮速度及负载矿粒的能力有差异。
2.2 活化剂和捕收剂的用量对石英相对接触角和浮选行为的影响为了考察活化剂和捕收剂用量对浮选效果的影响,固定矿浆pH值为12,活化剂(氯化钙)和捕收剂(油酸钠)按探索试验获得的最适配比4: 3质量比进行添加,氯化钙和油酸钠所用浓度均为25 mmol/L,氯化钙添加的浓度分别为0、1.25、2.5、3.75、5.00、6.25 mmol/L,油酸钠添加浓度分别为0、0.94、1.88、2.81、3.75、4.69 mmol/L,按照这种体积进行添加,测得(Δp)2-t关系,如图 5所示。
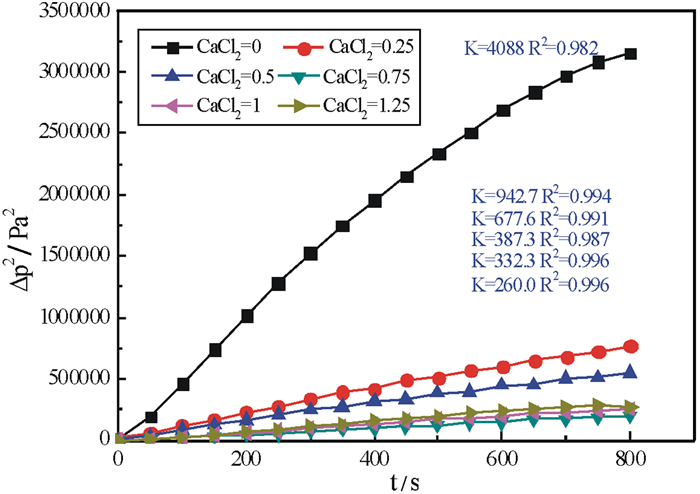 |
| 图 5 不同药剂条件下(Δp)2与时间t的关系曲线图 Fig.5 Relationship between (Δp)2 and t with different reagent concentrations |
由图 5可以看出,压差平方随时间的变化大致成一条直线,在未添加氯化钙和油酸钠的液体中,所得到的石英表面压差变化明显快于其他条件,当随着氯化钙和油酸钠浓度的增加,压差的平方变化越小,即去离子水的渗透速度越来越慢,反映了石英表面润湿性随着Ca2+和油酸钠浓度的增加而减小。
通过相应计算得出在氯化钙和油酸钠不同浓度时的相对接触角,并结合对应条件下的单矿物浮选所得到的回收率,结果如图 6所示。
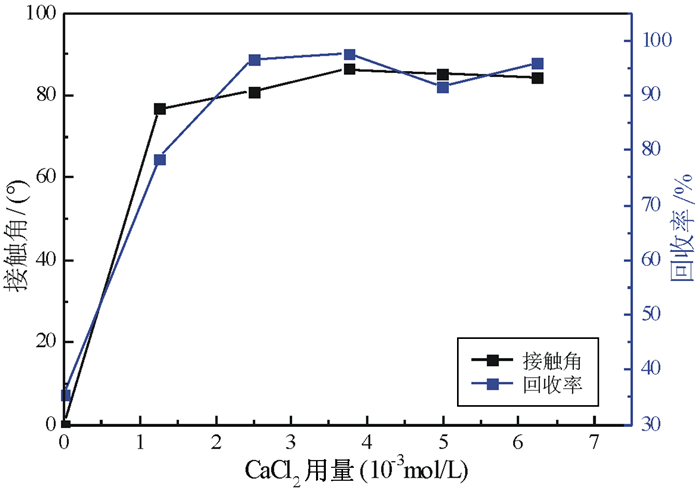 |
| 图 6 相同pH条件下,不同用量的CaCl2石英相对接触角和产率 Fig.6 Relative contact angel and quartz recovery with different reagent concentrations |
由图 6可以看出,测得的相对接触角与产率变化规律一致,这就证实了改变溶液中的Ca2+浓度和油酸钠的浓度确实会极大的影响石英表面的润湿性,从而影响浮选结果。随着氯化钙用量的增加,石英的产率急剧增加,当氯化钙的用量为3.75×10-3 mol/L时,石英的产率达到最大。
关于Ca2+与石英表面的作用机理,Fuerstenau等[21]认为Ca(OH)+离子会吸附在石英表面,而王淀佐等[22]则根据浮选溶液化学计算得到在石英开始浮选的pH值内,氢氧化钙是主要存在形式。寇珏等[23]测定了不同钙离子浓度下石英的Zeta电位,结果表明,随着Ca2+的添加,石英表面Zeta电位总体向正值方向移动,从而使阴离子捕收剂油酸钠吸附在石英表面,浓度越大,Zeta电位增加的越明显,因此得到较好的浮选效果。
若用油酸钠的用量来表示图 6所示关系,用其表示的相对接触角与浮选回收率与图 6所示的趋势相同,只是横坐标表示的含义改变了,在此处不予列出。因为油酸钠和氯化钙为最适配比(3: 4),对应图 6氯化钙的用量可以计算得到相应的油酸钠的用量,通过计算可知油酸钠用量从0增加到1.95×10-3 mol/L时,石英的回收率和相对接触角均急剧增大,之后二者随着油酸钠浓度升高缓慢增大,当油酸钠浓度为2.81×10-3 mol/L时其回收率最高,继续增加油酸钠浓度,回收率略有下降。
邱继存等[24]认为油酸钙的溶度积远小于氢氧化钙的溶度积,油酸钠的过量添加会导致吸附在石英表面的油酸钙量降低,从而导致回收率下降。而石云良等[25]则认为过量油酸钠的半胶束反向吸附现象会导致石英回收率降低。
综合分析图 2、图 3、图 5可知,使用Washburn法测得的压力差的平方(Δp)2与时间t存在线性关系,在不同药剂条件下其升高速度不同,计算得到的斜率k不同。之后再计算相对接触角由相对接触角的计算值可以看出,使用药剂的量不同确实使得石英颗粒的表面润湿性发生了改变。同时,结合对应条件下石英的浮选回收率及变化趋势分析(如图 4、图 6所示),可以清晰地看到,渗透法可以准确地体现颗粒表面的润湿性特征和可浮性特征,进而体现不同药剂条件下的颗粒的润湿性差异和可浮性差异。上述诸图表明,在pH值为12、氯化钙浓度为3.75×10-3mol/L、对应的油酸钠浓度为2.81×10-3 mol/L时,石英表面最易被钙离子活化,测得的接触角也最大,可浮性最强,因此其浮选回收率最高。
 |
| 图 3 不同pH条件下(Δp)2与时间t的关系曲线图(不包含去离子水) Fig.3 Relationship between (Δp)2 and t under different pH conditions (except deionized water) |
2.3 不同条件下溶液的表面张力以及体系相对自由能的变化
颗粒的疏水性的改变会影响接触角的大小,颗粒亲水时,接触角减小;颗粒疏水时,接触角增大。而接触角的变化又会影响体系自由能的变化,接触角增大,体系的自由能减少量增大,体系自由能的变化能够体现颗粒的可浮性和颗粒表面的特性。不同条件下所测得的矿浆滤液的表面张力以及相应的接触角的自由能变化量如图 7、图 8所示。
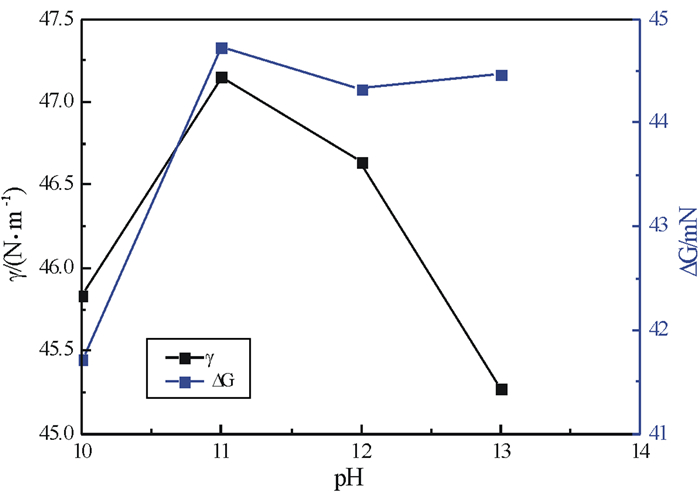 |
| 图 7 不同pH值下溶液的表面张力和体系自由能的变化量 Fig.7 Surface tension and ΔG of quartz under different pH conditions |
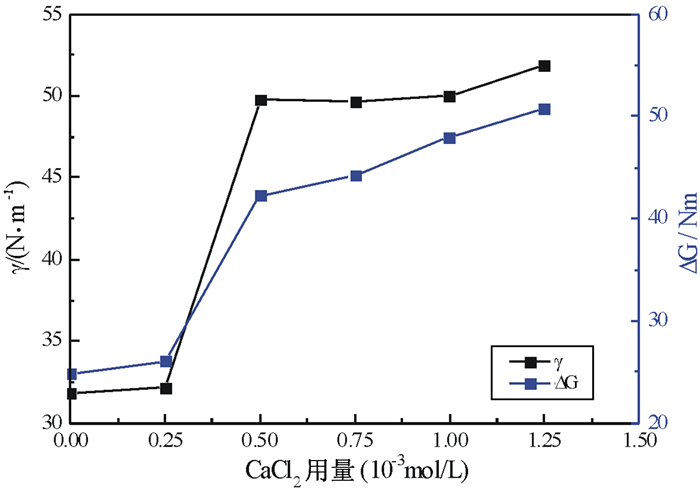 |
| 图 8 不同药剂条件下溶液的表面张力以及体系相对自由能的变化 Fig.8 Surface tension and ΔG of quartz with different reagent concentrations |
由图 7、图 8可知,ΔG的大小会受到pH值的影响,当pH小于11时,ΔG随着pH的增大而增大;当pH=11时,ΔG达到最大值,之后随着pH的增大,ΔG的值开始变小。而当溶液的pH值一定时,改变氯化钙和油酸钠的用量(氯化钙和油酸钠的4: 3配比),ΔG的大小随着氯化钙和油酸钠的用量的增加而增加。总的来说,虽然不是在pH=12的时候达到最大值,但是体系的相对自由能的变化量的变化趋势与接触角和回收率的变化趋势还是基本符合。随着颗粒的接触角变大,其附着在气泡前后的自由能的变化量也越大,这也就导致了颗粒的疏水性越强,其与气泡的结合越容易,可以自发地结合到气泡表面,并随之上浮,从而提高了浮选的效率。
当氯化钙和油酸钠的用量保持不变时,矿浆滤液的表面张力随着pH的改变先增大而后减小;当pH值保持不变的时候,改变氯化钙和油酸钠用量,可以发现表面张力随着药剂用量的增加而增大。结合表面自由能变化公式可知,表面张力越大,体系自由能的变化量越大,导致颗粒容易与气泡发生黏附。然而,矿浆的表面张力对气泡的尺寸和泡沫的稳定性也会产生影响,从而影响浮选的效果。
需要注意的是,当pH=11时,测得的表面张力和体系自由能变化量都大于pH=12时的值,石英颗粒接触角和产率与之相反。造成这种现象的原因可能是溶液的表面张力致使不同pH条件下气泡兼并的程度不同。
3 结论(1) 接触角计算结果和浮选试验结果表明,应用Washburn原理测得的相对接触角能够反映细粒石英表面的润湿性,接触角越大可浮性越好,浮选所得回收率越高。此方法操作方便,且不需要找到相应的完美润湿液体,可应用于定量比较颗粒的可浮性。
(2) 通过石英单矿物浮选试验,确定了利用油酸钠回收-0.045+0.037 mm粒级石英的最佳药剂条件:pH值为12,氯化钙用量为3.75×10-3 mol/L,油酸钠用量为2.81×10-3 mol/L,可为以石英为脉石矿物的矿石反浮选工艺的药剂用量选择提供一定参考。
(3) 颗粒与气泡附着前后体系的自由能的变化与颗粒表面接触角和溶液表面张力密切相关, 颗粒表面的接触角越大,越容易与气泡黏附并随气泡一起上升,浮选效果越好。与此同时,溶液的表面张力会对体系自由能变化产生影响,因此需要进一步深化理论研究工作,确定浮选最佳表面张力及其对浮选效果的具体作用。
| [1] |
魏德洲. 固体物料分选学:第三版[M]. 北京: 冶金工业出版社, 2015, 316.
|
| [2] |
Smedley GT, Coles DE. A refractive tilting-plate technique for measurement of dynamic contact angles[J]. J Colloid Interface Sci, 2005, 286(1): 310-8. DOI:10.1016/j.jcis.2005.01.090 |
| [3] |
徐志钮, 律方成, 赵鹏, 等. 拟合方法用于硅橡胶静态接触角的测量[J]. 高电压技术, 2009(10): 2475-2480. |
| [4] |
徐志钮, 王国利, 赵丽娟, 等. 亲水性时静态接触角算法及在硅橡胶憎水性检测中的应用[J]. 高电压技术, 2012(8): 1891-1900. |
| [5] |
徐志钮, 律方成, 张翰韬, 等. 影响硅橡胶静态接触角测量结果的相关因素分析[J]. 高电压技术, 2012(1): 147-156. |
| [6] |
丁晓峰, 管蓉, 陈沛智. 接触角测量技术的最新进展[J]. 理化检验(物理分册), 2008, 44(2): 84-89. |
| [7] |
张世举, 程延海, 邢方方, 等. 接触角与表面自由能的研究现状与展望[J]. 煤矿机械, 2011(10): 8-10. DOI:10.3969/j.issn.1003-0794.2011.10.004 |
| [8] |
王晓东, 彭晓峰, 陆建峰, 等. 接触角测试技术及粗糙表面上接触角的滞后性Ⅱ:粗糙不锈钢表面接触角的滞后性[J]. 应用基础与工程科学学报, 2003(3): 296-303. |
| [9] |
Chau TT. A review of techniques for measurement of contact angles and their applicability on mineral surfaces[J]. Minerals Engineering, 2009, 22(3): 213-219. DOI:10.1016/j.mineng.2008.07.009 |
| [10] |
Budziak C.J, Neumann A.W. Automation of the capillary rise technique for measuring contact angles[J]. Colloids and Surfaces, 1990, 43: 279-293. DOI:10.1016/0166-6622(90)80293-D |
| [11] |
Rodríguez-Valverde M A, Cabrerizo-Vílchez M A, Rosales-López P, et al. Contact angle measurements on two (wood and stone) non-ideal surfaces[J]. Colloids and Surfaces A:Physicochemical and Engineering Aspects, 2002, 206(1-3): 485-495. DOI:10.1016/S0927-7757(02)00054-7 |
| [12] |
Tomlison Fort Jr., Patterson H.T. A simple method for measuring solid-liquid contact angles[J]. Journal of Colloid Science, 1963, 18: 217-222. DOI:10.1016/0095-8522(63)90013-8 |
| [13] |
Anna Zdziennicka, Katarzyna Szymczyk, Joanna Krawczyk, et al. Some remarks on the solid surface tension determination from contact angle measurements[J]. Appl Surf Sci, 2017, 405: 88-101. DOI:10.1016/j.apsusc.2017.01.068 |
| [14] |
Kwok DY, Budziak CJ, Neumann AW. Measurements of static and low rate dynamic contact angles by means of an automated capillary rise technique[J]. Journal of Colloid and Interface Science, 1995(1): 143-150. |
| [15] |
Extrand C.W., Sung In Moon. Measuring contact angles inside of capillary tubes with a tensiometer[J]. Journal of Colloid And Interface Science, 2014, 431. |
| [16] |
Atefi E, Mann A J, Tavana H. A robust polynomial fitting approach for contact angle measurements[J]. Langmuir, 2013, 29(19): 5677-5688. DOI:10.1021/la4002972 |
| [17] |
Washburn E. The dynamics of capillary flow[J]. Physics Review, 1921, 17(3): 273-283. DOI:10.1103/PhysRev.17.273 |
| [18] |
陈国平, 陈邦林, 韩庆平. 渗透压力法测定粉体接触角[J]. 大学化学, 1992(5): 38-41. DOI:10.3866/PKU.DXHX19920509 |
| [19] |
韩德刚. 化学动力学基础[M]. 北京: 北京大学出版社, 1988.
|
| [20] |
王淀佐, 邱冠周, 胡岳华. 资源加工学[M]. 北京: 科学出版社, 2005, 196-197.
|
| [21] |
Fuerstenau M C, Miller Jan D, Pray R E. Metalion activation in xanthate flotation of quartz[J]. Transactions of the American Institutetute of Mining, 1965, 232: 359-364. |
| [22] |
王淀佐, 胡岳华. 浮选溶液化学[M]. 长沙: 湖南科学技术出版社, 1988, 132-148.
|
| [23] |
寇珏, 郭玉, 孙体昌, 等. 2种阴离子捕收剂在石英表面的吸附机理[J]. 中南大学学报(自然科学版), 2015, 46(11): 4005-4014. DOI:10.11817/j.issn.1672-7207.2015.11.005 |
| [24] |
丘继存, 郭永文. 多价金属阳离子对石英浮游的活化机理[J]. 有色金属(冶炼部分), 1965(7): 35-43. |
| [25] |
石云良, 邱冠周, 胡岳华, 等. 石英浮选中的表面化学反应[J]. 矿冶工程, 2001, 21(3): 43-45, 48. |
 2018
2018 


