正因为有了连续性，实数集才比有理数集较为优越而成为数学分析的“活动基地”.从几何直观角度来看，实数集的连续性就是用数轴上表示实数的点是连续分布的，再也没有“空隙”；而从分析角度来阐述，就有实数连续性的六个等价的基本定理. ^[1]国内大多数学分析教材 (比如文[1-2]等) 选取“确界存在性定理”作为实数集连续性的表述基石，成为极限理论的出发点.因此，确界概念的特征定义和确界存在性的证明思想方法的理解成为数学分析的学习核心.

确界 (上确界和下确界的统称) 是在大学一年级新生数学分析课程的第一章节中第一次涉及具有极限思想的概念，它的形式逻辑符号语言表述和推理论证方式让初学者感到难以适应，觉得高度抽象难以理解，运用时不知如何表述.根据多年从事数学分析的教学实践看，笔者看到，大一理科生第一次面对蕴含有极限思想的确界概念，却出现了感到别扭和困惑等难以理解的学习窘境.实际上，这方面的感受也是很多从事数学分析教学的教师们所共鸣的，从文献[6-9]等可略见一番.究其原因，初学者对确界用两个形式逻辑语言进行抽象刻画出确界概念一时难以适应，把握不住要领.比如数集S的元素一会用“x”一会用“x′”或“α, β”表示，确界用希腊字母“ξ, η”表示，还结合拉丁字母“sup S, inf S”表达，运用时在证明最小上界或下界的表述不那么好操作.教材^[1]采用无限次十等分区间来构造一个准确界的无限小数η=n.n₁n₂…n_k…的思想方法也很困惑，对于每个数码n_k所在的区间又要做一定的信息限制：1) 任意x∈S有x＜n.n₁n₂…n_k+10^-k；2) 存在a_k∈S使a_k≥η＝n.n₁n₂…n_k.论证的过程，还要考虑反证法，有时取x∈S的k为不足近似值x_k与η的过剩近似值η_k比较，有时截取x∈S的k为过剩近似值x_k与η的不足近似值η_k比较.面对这么众多的符号信息切换和在无限小数和有限小数之间穿梭腾挪的大跨度变动，初学者由于中学的“重计算能力培养轻数学逻辑思维”的训练习惯，一时难以适从，加上阐述表达能力的有限，难以对多个因果关联思维进行掌控.

为改变这一现状，笔者采用一些可视化和迂回补充的手法来改进确界及其存在性的学习和教学方法，这不是为了把确界和确界存在性的论证方法复杂化，而是想引用一些更加朴实、非常通俗的例子作寓意或启迪，给初学者带来看得懂、听得懂的方法，不再为教材的一家之言所困扰，能从多角度去理解和领悟.同时，强化符号就得更多的注入，而不是回避甚至减少符号的出现.推进学生的思维逻辑，不能埋怨教材处理的篇幅长度而力求阐述得有理有节，更不能牺牲逻辑的严谨，关键是对论证的思维脉络清晰以及文字表述和一定的文学素养训练，学生只有尽快适应大学的这种理论化系统化的风格，才能有意识地切断中学惧怕证明书写的毛病，合乎大学理科专业教学的本质.

本文研究的教学角度不同于文献[6-9]的研究, 紧扣从确界的描述性定义到精确的逻辑语言定义时学生碰到的理解困难，利用多个角度直观可视化地剖析上确界、下确界；对于数集的确界存在性定理，利用十等分法从无限小数截取不足近似和过剩近似的逆向过程构造有上界或下界的非空数集的上确界或下确界，结合确界的无穷小数逼近表示法和确界的集合分划理念进行变式教学.为了实现教学目标，结合当前扩招下学生的逻辑强化不够的现状，引进分划方法来推动学生们更好地理解确界的本质和综合运用能力.最后，本文还就实数的无限小数表示给出一种新约定以利于证明过程中无限小数各个数码所在半开区间的写法统一，通过这种扩展探究来强化确界存在性证明思想的深度认知.

1 确界的定义和两个角度的剖析 1.1 确界的产生背景——数集的最大数和最小数

实数集$\mathbb{R}$的各种子集简称数集.对于数集$S\subset \mathbb{R}$，从小学到中学教育的熏陶，让初学者很自然地感兴趣于S的最大数或最小数.有别于高中所学的最大值和最小值，这里S的最大数或最小数采用形式符号表述.

定义1^[2-4] 一个元素ξ称为数集S的最大数，如果ξ∈S且任意x∈S都有x≤ξ；一个元素η称为数集S的最小数，如果ξ∈S且任意x∈S都有x≥ξ.

引入一些符号，给最大数和最小数一种更加简明的形式符号表述：^[3]

$\begin{align} & \left( \xi =\max \ S=\underset{x\in S}{\mathop{\max \ x}}\, \right):\left( \xi \in S\wedge \forall x\in S\left( x\le \xi \right) \right); \\ & \left( \eta =\min \ S=\underset{x\in S}{\mathop{\min \ x}}\, \right):\left( \xi \in S\wedge \forall x\in S\left( x\ge \xi \right) \right); \\ \end{align}$

(1)

这里max S读作“S的maximum”，min S读作“S的minimum”，而“∧, ∨, $\neg $”为布尔代数的逻辑演算的形式符号“且and，或or，非not”.

显然，当数集S为有限集时，max S和min S分别为这有限个元素中的最大者和最小者.然而，并不是每一个数集都拥有最大数和最小数，例如，${{S}_{1}}=\left\{ x\in \mathbb{R}\left| 0＜x\le 1 \right. \right\}$有最大数1没有最小数；${{S}_{2}}=\left\{ x\in \mathbb{R}\left| 0\le x＜1 \right. \right\}$有最小数0没有最大数；有理数集${{\mathbb{Q}}_{r}}\subset \left( 0,1 \right)$既不存在最大数也不存在最小数.

为弥补这方面缺陷，引进更加泛化的术语——上确界和下确界.这会牵涉相关的概念：数集的上/下有界，数集的上/下界，确界.

1.2 数集上有界、上界及上确界

定义2^[3-4] 对于考察的非空数集S，若存在这样的有限实数$M\in S\bigcup {{S}^{C}}=\mathbb{R}$，使得一切$S\backepsilon x\le M$，则说数集S(被M) 上有界 (bounded above)，而数M称为数集S的一个上界 (upper bound)；如果存在这样的有限实数$m\in S\bigcup {{S}^{C}}=\mathbb{R}$，使得一切$S\backepsilon x\ge m$，则说数集S为 (被m) 下有界的 (bounded below)，而数m称为数集S的一个下界 (lower bound)；如果S既有上界又有下界，则称S为有界集；如果S无上界或无下界，则称S为无界集.

从定义2容易看出，自然数集${{\mathbb{N}}^{+}}$被数1或任何小于1的数下有界，但不是上有界；正的真分数集被1上有界又被0下有界.进而，我们推知S是被M上有界的数集，则S必有无数多个上界 (任何大于M的数)，人们比较感兴趣或觉得特别有用的是在一切上界中那个最小的上界 (将称为上确界).同样地，被m下有界的数集S必定拥有无数多个下界 (凡是小于m的数)，人们比较感兴趣是当中最大的下界 (将称为下确界).现在遇到的问题是：上有界的数集S的一切上界中是否存在最小的上界？下有界的数集S的一切下界中是否存在最大的下界呢？这还需要加以证明，见后边的确界存在性定理.作为先验定义，人们先给出不依赖确界存在性定理的上 (下) 确界的定义.

为了让学生更好地理解上确界 (最小上界) 和下确界 (最大下界的定义)，除了教材[1-2]的定义外，我们给出另一种与之等价的定义.通过文字语言、符号语言及图形来帮助学生对抽象概念的理解.

首先我们应该清楚的是，上确界有两层含义，用文字语言描述如下：

Ⅰ) 上确界是集合的一个上界；

Ⅱ) 上确界是所有上界中最小的一个，所谓最小指凡是小于它的任何一个数都不再是该集合的上界.

接着，我们给出两种形式语言符号来表述上确界的两个特征：上界的不等式和最小上界的不等式，精确定义如下. ^[1-3]

定义3 实数η称为数集S的上确界，记作η=sup S，如果它满足以下两个条件：

Ⅰ)η是S的上界：∀x∈S，有

$x\le \eta ;$

(2)

Ⅱ) 任何小于η的数不再是S的上界：∀α＜η，∃x₀∈S，有

${{x}_{0}}>\alpha .$

(3)

注意到上确界的条件Ⅱ) 还可以简化.因为只要在η的ε左邻域取一个数，不妨取η-ε，如果存在x₀∈S使得x₀>η-ε，那么对于所有小于η-ε的数α，自动有x₀>α.因此上确界还可以用ε语言来刻画.

定义3′ 有限实数η称为数集S的上确界，记作η =sup S，如果

Ⅰ) ∀x∈S，有x≤η；

Ⅱ) ∀ε>0，∃x₀∈S，使得

${{x}_{0}}>\eta -\varepsilon .$

(3′)

定义3和定义3′完全用形式逻辑符号表述如下:^[3]

$\begin{align} & \quad \left( \eta =\sup \ S \right):=\left( \forall x\in S\left( x\le \eta \right) \right)\ \wedge \forall \alpha ＜ \\ & \eta \left. \left( \exists S\backepsilon {{x}_{0}}>\alpha \right) \right), \\ & \quad \left( \eta =\sup \ S \right):=\left( \forall x\in S\left( x\le \eta \right) \right)\ \wedge \forall \varepsilon > \\ & 0\left. \left( \exists S\backepsilon {{x}_{0}}>\eta -\varepsilon \right) \right). \\ \end{align}$

(4)

这种处理形式的优点一是更为简洁，二是便于运用时进行逻辑推理的书写或阐述的方便.

注1：从定义3和等价定义3′看，上确界概念主要特征是通过不等式 (2) 和 (3) 或 (3)′来刻画的.这种方式的定义极其简明，但简明并不意味着一定容易理解和操作.事实上，初学者对这样的形式定义还是感到别扭和迷惑，主要符号多，涉及了η=sup S，α, ε, x，x₀, 还有任意符号∀，存在符号∃，形式上虚虚实实.这种架势，是刚脱离高中不久的大一新生所没有见过和曾得到强化训练过的.

1.3 数集下有界、下界及下确界

仿照数集上确界的定义，下面给出具有对称的下确界的定义.

首先，下确界也有两层含义，文字语言表述如下：

ⅰ) 下确界是集合的一个下界；

ⅱ) 下确界是所有下界中最大的一个，所谓最大即凡是大于它的任何一个数都不再是该集合的下界.

接着，根据上确界的两个特征，用两种等价的形式语言符号来刻画下界的不等式和最大下界的不等式，得到下确界的精确定义如下. ^[3]

定义4 有限实数ξ是数集S的下确界，记作, ξ= inf S如果它满足以下两个条件：

ⅰ)ξ是S的下界：∀x∈S，有

$x\ge \xi ;$

(5)

ⅱ) 任何大于ξ的数不再是S的下界：∀β>ξ，∃x₁∈S, 使得

${{x}_{1}}＜\beta .$

(6)

定义4′ 有限实数ξ是数集S的下确界，记作ξ=inf S，如果

ⅰ) ∀x∈S，有x≥ξ；

ⅱ) ∀ε>0，∃x₁∈S, 使得

${{x}_{1}}＜\xi +\varepsilon .$

(6′)

定义4和定义4′也可以用更加简洁的形式逻辑符号表述如下:^[3]

$\begin{align} & \quad \left( \xi =\inf \ S \right):=\left( \forall x\in S\left( x\ge \xi \right) \right)\ \wedge \forall \beta > \\ & \xi \left. \left( \exists S\backepsilon {{x}_{1}}>\beta \right) \right), \\ & \quad \left( \xi =\inf \ S \right):=\left( \forall x\in S\left( x\ge \xi \right) \right)\ \wedge \forall \varepsilon > \\ & 0\left. \left( \exists S\backepsilon {{x}_{1}}>\xi +\varepsilon \right) \right). \\ \end{align}$

(7)

注2：注意，上确界、下确界与最大值、最小值存在微妙的区别.由上确界的定义知，数集的最大数一定是上确界，反之不然.例如，S₁={x∈$\mathbb{R}$|0＜x≤1}有上确界sup S₁=max S₁=1，下确界inf S₁=0而min S₁不存在；S₂={x∈$\mathbb{R}$|0≤x＜1}有下确界sup S₂=min S₂=0，上确界sup S₂=1而max S₂不存在.数集S={x|x为区间 (0，$\sqrt{2}$) 的有理数}分别有上下确界sup S=$\sqrt{2}$，inf S=0，但max S和min S都不存在.

注3:在具体运用上确界或下确界的不等式特征表述最小上界或最大下界不那么好操作，需要用到其他信息，如有理数在实数中的稠密性，这是初学者普遍感到比较吃力的地方.比如，对于S={x|x为区间 (0，$\sqrt{2}$) 的有理数}，用上确界的定义证明sup S=$\sqrt{2}$如下：首先对一切有理数x∈S，由于S⊂(0, $\sqrt{2}$)，所以x＜$\sqrt{2}$，即$\sqrt{2}$是S的下界；另一方面，对任何实数α＜$\sqrt{2}$，若α＜0，这时∀x₀∈S，x₀>0，当然x₀>α；若α>0，则由有理数集在实数集中的稠密性，在 (α, $\sqrt{2}$) 内必存在有理数x₀，从而x₀∈S且x₀>α，即α不再是S的上界.

1.4 确界的几何直观及折中合理的新术语——右/左界及右/左确界

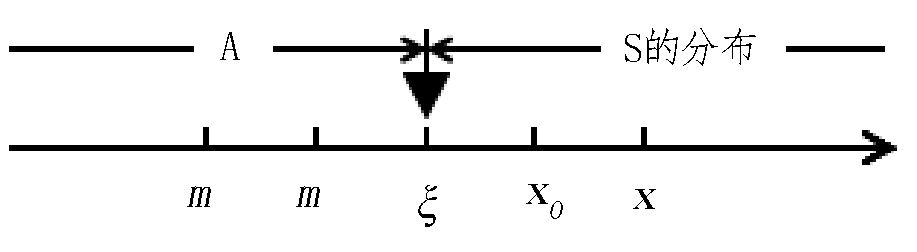
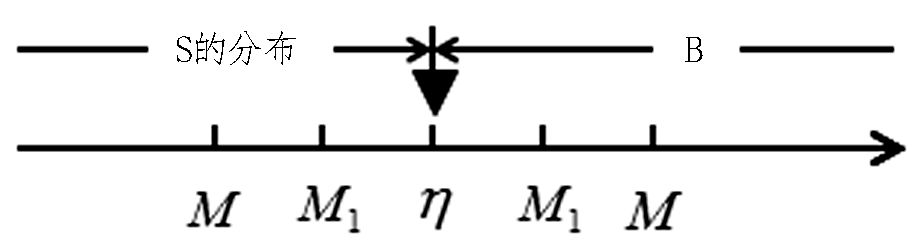
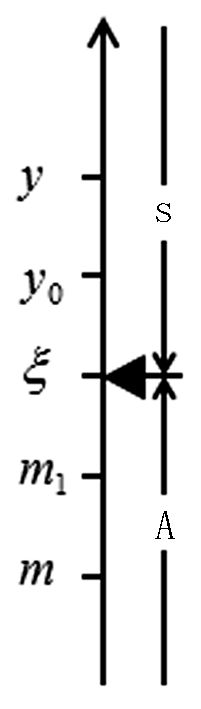
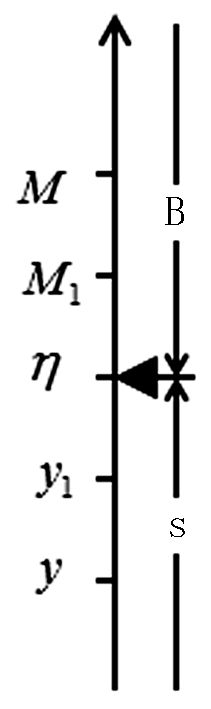
为了让学生从直观或可视化的角度上理解确界的抽象定义，我们可以通过水平数轴或垂直轴 (竖轴) 绘出示意图来帮助学生理解上/下确界的本质.

图 1和图 3中，A={m∈$\mathbb{R}$|m为S的下界}，水平数轴上数集S左边的点 (或S下边的点)m, m₁, m₂, …都是S的下界，下确界是数集S在水平 (垂直) 数轴上的最左 (下) 端与下界集合A的零距离接触点 (公共界点).类似地，图 2和图 4中，B={M∈$\mathbb{R}$|M为S的上界}，水平数轴上数集S右边的点 (或S上边的点)M, M₁, …都是S的上界，上确界是数集S在水平 (垂直) 数轴上的最右 (上) 端与下界集合B的零距离接触点 (公共界点).零距离接触意味着无论数集S所表示的区间一端是开的还是闭的，上或下确界都能取到那个数，而最大值或最小值在右端点或左端点必须是闭时才能取到.

对于上界、下界、上确界和下确界，初学者感到有点费解的地方是从概念的定义看似乎谈论右界、左界、右确界和左确界更显得自然些.理由是从几何的示意图来直观理解，上界、下界、上确界和下确界应该是按从下往上为正方向的垂直数轴来刻画：有上界的数集S的上界必然落在S的上边点，上确界只不过是S的最上端与集合B={M∈$\mathbb{R}$|M为S的上界}的界点数；有下界的数集S的下界必然落在S的下边点，下确界只不过是S的下端与集合A={m∈$\mathbb{R}$|m为S的下界}的界点数.但习惯上，更多是以向右边为正方向的水平数轴表示实数$\mathbb{R}$，数集S占据数轴上的某些连续或离散的片段，根据数轴上右边的数总比左边的大，有上界的数集S的上界必然落在S的右边，上确界只不过是最靠近S的右端临界点；有下界的数集S的下界必然落在S的左边点，下确界只不过是最靠近S的左端临界点.所以，初学者希望“上界、下界、上确界和下确界”也可以分别叫作“右界、左界、右确界和左确界”.

教者如能告诉他们，这种叫法也是合理的，的确有些国外教材如俄罗斯教材^[4-5]支持这种说法，那么学生学习的内在心理会感到很愉悦，喜欢这类暂时陌生的术语并愿意作进一步的接纳其他信息和探索.

接下来初学者希望授课者给出这两种叫法的合理性.这时，授课者就会借机推动学生的求知探索欲望，指出数学分析面向的对象是函数y=f(x)，后边章节会出现函数的“上/下极限”与“左/右极限”，所谓“左右”只不过相对于自变量x而言，而所谓的“上下”不过对因变量即函数值而言.

类似地，对于函数

$y=f\left( x \right)=\left\{ \begin{array}{*{35}{l}} x,0\le x＜1 \\ 0,x=1 \\ \end{array} \right.$

很显然在定义区间D=[0, 1]上有上确界1和下确界0，下确界是在x=0及x=1时的最小函数值，上确界不是函数值而是f(x) 在x=1的左极限.相对于自变量x而言，谈论左/右确界；相对因变量y而言，谈论值域S=f(D)=[0, 1) 的上/下确界.可见，上下确界和左右确界是有统一和谐之处.尽管如此，值得提醒初学者的是正规或常用的术语还是上/下确界，免得日后讨论交流时产生不必要的障碍.

1.5 确界的原汁原味在于希腊文和英文

上确界也叫最小上界，毕竟是从拉丁文或英文翻译过来的中文名，不一定能切合愿意，所以为了调动学生的学习热情，让学生更好地理解，教者给出带有原汁原味的3个词源: superemun, exact upper bound, least upper bound.下确界也叫最大下界，对应的拉丁文和英文词为infrimun, exact lower bound, greatest lower bound.建议学生课后到网上或找英汉词典查阅.

1.6 确界的否定陈述

在逻辑推理中，我们会遇到上确界的否定表述.弄清怎样从上确界的正命题给出相应的反命题，对比正反两方面命题有利于加深对上确界概念的认知.上确界定义的反命题叙述如下：

实数η不是数集S的上确界：sup S≠η⇔或者η不是上界：∃x₀∈S使得x₀>η; 或者η不是最小的上界∃ε₀>0, 对∀x∈S有x≤η-ε₀.

或 (sup S≠η):=(∃x₀∈S(x₀>η)∨∃ε₀>0(∀S∋x≤η-ε₀)).

类似地，下确界定义的反命题可叙述如下：

实数ξ不是数集S的下确界：inf S≠ξ⇔或者ξ不是下界：∃x₁∈S使得x₁＜ξ; 或者ξ不是最大的下界∃ε₀>0, 对∀x∈S有x≥ξ+ε₀.

或 (inf S≠ξ):=(∃x₁∈S(x₁＜ξ)∨∃ε₀>0(∀S∋x≥ξ+ε₀)).

2 确界存在性定理的变式教学

上一节从推广最大值或最小值的角度，给出了数集的确界 (上确界和下确界) 的定义，再从几个角度进行教学尝试.本节将回答前面提到的问题：上有界的数集S的一切上界中是否存在最小的上界？下有界的数集S的一切下界中是否存在最大的下界呢？回答是肯定的，这正是下面的确界存在性定理. ^[1]7

定理1 (确界存在性定理——实数连续性定理) 非空上有界的数集S必有上确界；非空下有界的数集S必有下确界.

教材[1]主要通过构造无限小数的方式来论证确界的存在性，由于证明过程冗长，涉及的步骤多，符号多，概念术语多，中间还使用反证法，特别不断截取无限小数的不足近似值和过剩近似值进行有限比较获证上确界或下确界的两个特征不等式 (2) 和 (3) 或 (5) 和 (6)，这种高跨度高信息交融的逻辑推理论证，初学者有招架不住的感觉.为此，我们不是避难就轻，牺牲数学分析的逻辑严谨为代价，而是迎难而上，采用分段式和分层次的处理方式，并通过设计引申题来强化学生对高密度思维的模仿、适应和忍耐力，克服畏难情绪、厌烦心理，这是学习数学分析所必须具有的品质和面临的情景.

为了能使初学者深入浅出的理解上述定理的证明思想，我们从两方面来进行变式教学研究.

2.1 戴德金 (R. DedeKind) 的集合分划

不用习惯的十进制数，并摆脱“极限”概念的束缚，戴德金只用有理数的性质和集合的概念，给出下面简明的有理数分划定义引出新数——无理数, ^{[1]298-299, [2]30, [5]10, [4]6}在历史上被誉为人类智慧的创造物.

定义5 若将有理数集$\mathbb{Q}$分拆成两个非空子集A，B, 使得

1°任意有理数必在且仅在A和B之一中出现：A∪B=$\mathbb{Q}$, A∩B=$\varnothing $；

2°集A的任一数a必小于集B的任一数b：∀a∈A, ∀b∈B，有a＜b，

则称A和B构成$\mathbb{Q}$的一个分划，其中A称为分划的下组，B称为分划的上组；分划记为A|B.

注4：很明显，不可能有这样$\mathbb{Q}$的分划A|B存在：在它的下组A内有最大数a₀而同时在上组B又有最小数b₀.否则由定义的2°知a₀＜b₀，根据有理数的稠密性，a₀和b₀之间有很多有理数，这与分划定义的1°矛盾.

有理数分划只能出现如下3种类型：

1) 下组A内无最大数，而上组B内有最小数r，比如，令{a∈$\mathbb{Q}$|a＜1}=A，{b∈$\mathbb{Q}$|b≥1}=B，则r=1为A和B的界数，或说分划A|B定义了有理数1；

2) 下组A内有最大数r，而上组B内无最小数，比如，令{a∈$\mathbb{Q}$|a≤1}=A，{b∈$\mathbb{Q}$|b>1}=B，则r=1为A和B的界数，或说分划A|B定义了有理数1；

3) 下组A内无最大数，而上组B内也无最小数，比如，令

$\begin{align} & \quad \left\{ a\in \mathbb{Q}\left| {{a}^{2}}＜2,a>0 \right. \right\}\bigcup \left\{ a\in \mathbb{Q}\left| {{a}^{2}}\le 0 \right. \right\}= \\ & A,\left\{ b\in \mathbb{Q}\left| {{b}^{2}}>2,b>0 \right. \right\}=B, \\ \end{align}$

则不存在有理数作为A和B的界数，或说分划A|B定义了一种新数——无理数$\sqrt{2}$.

可见，总可以把无理数理解为有理数集中确定的分划A|B.

2.2 实数的无限小数表示及亏盈近似值

由中学课本知道，无限循环小数表示有理数；反之，任意有理数总可化为循环小数.这样，不循环的无限小数就用来表示引入的无理数.因此，可以将实数想象为无限十进小数.^{[1, 5]}

实数η的十进小数近似值的过程中，就得到整数n₀及数码n₁, n₂, …, n_k, …的无限序列.由此序列组成的无限小数，即记号

${{n}_{0}}.{{n}_{1}}{{n}_{2}}\ldots {{n}_{k-1}}{{n}_{k}}\ldots $

(8)

可看作实数η的一种表示.

将小数 (8) 记为x=n₀.n₁n₂…n_k-1n_k…，考察它的一小段

${{x}_{k}}={{n}_{0}}.{{n}_{1}}{{n}_{2}}\ldots {{n}_{k-1}}{{n}_{k}}$

(9)

作为x的“k位不足 (亏) 近似”，^[1]2同样把

${{{\bar{x}}}_{k}}={{n}_{0}}.{{n}_{1}}{{n}_{2}}\ldots {{n}_{k-1}}{{n}_{k}}+{{10}^{-k}}$

(10)

作为x的“k位过剩 (盈) 近似”.^[1]2不难看出，${{x}_{k}}＜{{{\bar{x}}}_{k}}$.

2.3 定理1的集合分划构造证法

根据有理数分划的定义5和上一节无限小数总能找到一个实数恰好为这个实数所表示的证明过程所使用的技巧，我们可以给出定理2的一种简洁证法.^{[2]32, [4]}

由有理数分划的定义5及注记4，我们知道有理数虽然有稠密性但它们之间存在空隙，所以需要引进新数——无理数.如果将有理数$\mathbb{Q}$的一个分划A|B拓展到实数集$\mathbb{R}$的一个分划A|B，那么$\mathbb{R}$的分划A|B产生的界数就不会再溢出实数集，即实数之间不再有空隙，这个连续性或完备性事实正是下面的戴德金基本定理.^[4]12

定理2(戴德金基本定理) 对于实数集$\mathbb{R}$的任意分划A|B必产生这一分划的实数β存在，其中β或者是下组A的最大数，或者是上组B内的最小数.

利用这个定理2，就可以证明数集$S\subset \mathbb{R}$的一切上 (下) 界存在有最小 (最大) 数.

定理1的证明.先证定理的下半部论断：对于下有界的数集S，若S有最小数x，则inf S=min S=x.故只需考虑非平凡情形：min S不存在.首先，构造实数集的一个分拆如下：

{a∈$\mathbb{R}$|a为S的下界：∀S∋x>a}=A, B=A^C=$\mathbb{R}$-A.

在这样的分拆下，集S的一切数x将全部落在B内，故B≠$\varnothing $；由假定，S有下界且没有最小数，所以A≠$\varnothing $.根据构造，A∩B=$\varnothing $, A∪B=$\mathbb{R}$；同时，∀a∈A为S的下界且不是最小数，而∀b∈B不是S的下界，所以有a>b.于是，A和B构成了实数集$\mathbb{R}$的一个分划，根据戴德金基本定理2，分划A|B的界数ξ存在，且ξ=max A(因为∀x∈S⊂B，所以x不小于界数ξ，即ξ可作为S的下界，从而ξ∈A；再注意到界数η不会小于下组A的每个元素a).这样，ξ就成为S的最大下界，即ξ=inf S.

至于定理的上半部论断：不妨设max S不存在，作$\mathbb{R}$的一个分拆为：

{b∈$\mathbb{R}$|b为S的上界：∀S∋x＜a}=${\tilde{B}}$, $\tilde{A}={{{\tilde{B}}}^{C}}$=$\mathbb{R}$-${\tilde{B}}$,

则${\tilde{A}}$和${\tilde{B}}$构成了实数集$\mathbb{R}$的一个分划.根据戴德金基本定理2，分划${\tilde{A}}$|${\tilde{B}}$的界数η存在，且η=min ${\tilde{B}}$，进而证得η=sup S. ^{[2]32, [4]13-14}

2.4 定理1的构造无限小数作确界的证法探索

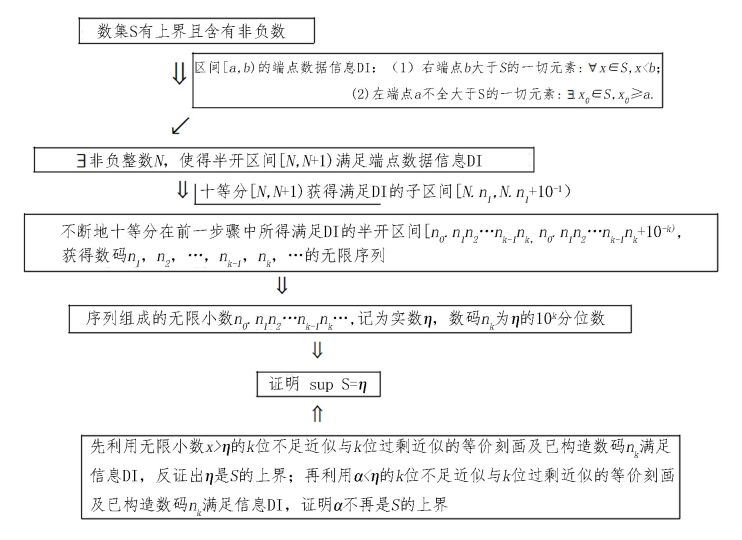
教材[1]通过上有界采用构造无限小数作为准上确界来论证确界存在性定理1，相对符合学生的认知心理和规律，但由于构造中涉及很多知识点信息，初学者的确感到有些复杂难懂.为了让学生更好地理解，下面给出将证明过程进行简化和改进，插入数轴示意图描述构造无限小数的个数码过程；证明之后给出清晰简明的证明思路示意图，指出关键的步骤和核心思路；对证明过程中学生普遍碰到的两个困惑进行注释.最后从教学角度给出引申问题的训练.

2.4.1 定理1的上确界结论证明

Step1 不妨设S含有非负数 (否则转证有下界的S^-={-x∈$\mathbb{R}$|x∈S}存在下确界).^[注5]由S有上界，可找到非负整数n，使得左开右闭区间[n, n+1) 满足^[注6]

1)n+1为S的上界非最小数：∀x∈S, x＜n+1；

2)[n, n+1)∩S≠$\varnothing $：存在a₀∈S，使a₀≥n.

Step2 通过十等分法在半开区间[n, n+1) 中构造出一个无限小数η=n.n₁n₂…n_k….

对半开区间[n, n+1) 作十等分，分点为n.1, n.2, …, n.9, 则存在一个十进制数码n₁，使得

1) 对于任何x∈S有x＜n.n₁+10^-1；

2) 存在a₁∈S，使a₁≥n.n₁.

再对半开区间[n.n₁, n.n₁+10^-1) 作十等分，则存在一个十进制数码n₂，使得

1) 对于任何x∈S有x＜n.n₁n₂+10^-2；

2) 存在a₂∈S，使a₂≥n.n₁n₂.

继续这样不断地十等分在前一步骤中所得的半开区间，在确定了小数位数码n₁, n₂, …, n_k-1后，十等分[n₀.n₁n₂…n_k-1, n₀.n₁n₂…n_k-1+10^-k+1) 定义第k位小数数码n_k，使得

1) 对于任何x∈S有x＜n.n₁n₂…n_k+10^-k；

2) 存在a_k∈S，使a_k≥n.n₁n₂…n_k.

这样，将上述步骤无限地进行下去，就得到整数n₀及数码n₁, n₂, …, n_k, …的无限序列.由此序列组成的无限小数n₀.n₁n₂…n_k-1n_k…，记为实数

η=n.n₁n₂…n_k….

Step3 利用已知事实^[1]2 “设x=a₀.a₁a₂…与y=b₀.b₁b₂…为两实数，则x>y的等价条件是：存在非负整数n，使得x_n>y_n，其中x_n表示x的n位不足近似，y_n表示y的n位过剩近似.”证明η=sup S.

先证Ⅰ)η是S的一个上界 (∀x∈S，有x≤η).

倘若结论Ⅰ) 不成立，则存在x₀∈S使x₀>η，由可找到某个非负整数k，使 (x₀)_k>η_k.

由于x₀>(x₀)_k, η_k=n.n₁n₂…n_k+10^-k从而得x₀>n.n₁n₂…n_k+10^-k，但这与数码n_k的构造要求n.n₁n₂…n_k+10^-k是S的一个上界发生矛盾，于是Ⅰ) 得证.

再证Ⅱ) η是S的最小上界.

对于∀α＜η，则存在某个正整数k使得η的k位不足近似η_k>α_k，由于α＜α_k，η_k=n.n₁n₂…n_k从而得n.n₁n₂…n_k>α.由数码n_k位的构造知∃a_k∈S，a_k≥n.n₁n₂…n_k, 从而a_k>α，α不是S的上界.这说明Ⅱ) 成立.

2.4.2 上面证明的思路示意如下 2.4.3 上述证明过程中的疑点注释

注5：对于这个“不妨”学生颇感费解和困惑.这需要教师指出合理性：有上界的S含有非负数，那它的上界都是非负数，构造出的无限小数作为准上确界是个非负数.这样做能回避负无限小数在截取k位不足近似和k位过剩近似所带来的麻烦，特别最后利用无限小数x₀>η或α＜η的k位不足近似和k位过剩近似的等价刻画来证明η是S的上界而α不是上界的过程.问题在于，假如S不含有非负数，则S全含负数，怎么办？这需要教师给学生补充一些常识：这时S关于数轴原点的对称集S^-={-x∈$\mathbb{R}$|x∈S}就转变为有下界且含正数的情形，只要证明S^-的下确界inf S^-存在，结合这样的关系sup S=-inf S^-就可间接获证.

注6：这是学生普遍感到困惑的问题：有上界的S含有非负数，怎么可以找到这样的非负整数n₀满足∀x∈S(x＜n₀+1)∧∃x₀∈S(x₀≥n₀)？一方面可以这样解释，假如这样的整数n₀不存在，则S是不可能有上界的，因为所有的整数n₀+1都不是S的上确界，这必然与“有理数在实数中稠密”相违背.如果还显得抽象的话，不妨设正数M是S的上界，则由M的取整[M]满足：[M]≤M＜[M]+1，知道[M]+1必然是S的上界，进而将[M]+1逐次减去1，经过适当的k次，必能找出这样相邻的非负整数n₀=[M]+1-k及n₀+1.更为直观的几何解释是，令数集B={b∈$\mathbb{R}$|b为S的上界：∀S∋x＜b}，则显然在数轴上，B在S的右边且它们之间有一个接触界点，设对应的实数为x₀，则[x₀]或[x₀]+1就是所期待的n₀.这里的[n₀, n₀+1) 不过为[0, 1), [1, 2), …之一.

2.4.4 教学的进一步扩展探究

为了检测学生们的理解与掌握情况，也为了激发学生们的学习兴趣与探索精神，结合刚学到的构造无限小数作为准上确界的证明方法，我们留3个课后习题给学生进行模仿创新练习，做题时间一周.为激发学生的学习动机，助于学生更好地掌握这一知识点与这一重要的数学思想方法，把这次作业作为段考的一部分，赋予一定的加分值，并考虑平时成绩的加权值.

【扩展思考题】

Q1:若不妨假设有上界的S不含有非负数，即S全为负数，该如何直接构造无限小数来证明？

Q2:若不妨假设有下界的S含有非正数，该如何直接构造无限小数来证明？

Q3:若不妨假设有下界的S不含非正数，该如何直接构造无限小数来证明？

考虑到下确界与上确界的定义不一样，负数的不足近似和过剩近似与非负数的不足近似和过剩近似存在一些微妙的区别，这给论证带来不少技术性的处理.为了减轻初学者的压力，我们对扩展思考题给些必要的提示.

Q1提示.若S全为负数，则存在某个非负整数n，使得左开右闭区间[-n-1，-n) 满足端点数据信息DI，十等分之得十进制数码n₁使半开区间[-n.n₁-10^-1, -n.n₁) 满足端点信息DI；依次不断地十等分在前一步骤中所得的半开区间，得到无限十进制数码序列n₁，n₂，…，n_k-1，n_k，…，每个数码n_k使半开区间[-n.n₁n₂…n_k-1n_k-10^-k, -n.n₁n₂…n_k-1n_k) 满足端点信息DI，从而得到一个无限小数-n.n₁n₂…n_k…，记为η；再证η=sup S，注意负无限小数η的k位不足近似η_k=-n.n₁n₂…n_k-1n_k-10^-k和k位过剩近似_k=-n.n₁n₂…n_k-1n_k.

Q2提示.有下界的S含有非正数，所以S的下界都是非正数，存在某个非负整数m，使得左开右闭区间 (-m-1, -m]满足端点数据信息DI′：左端点小于S的一切元素而右端点不全小于S的一切元素.然后十等分 (-m-1, -m]得十进制数码m₁使得半开区间 (-m.m₁-10^-1, -m.m₁]满足端点信息DI′；依次这样不断地十等分在前一步骤中所得的半开区间，得到无限十进制数码序列m₁, m₂, …, m_k-1, m_k, …，每个数码m_k使得半开区间[-m.m₁m₂…_k-1m_k-10^-k, -m.m₁m₂…m_k-1m_k) 满足端点信息DI′，从而得到一个无限小数-m.m₁m₂…m_k-1m_k…，记为ξ；接着证ξ=inf S，先证ξ为S的下界，再证β>ξ不再是S的下界.

Q3提示.有下界的S的元素全为正数，存在某个正整数m，使得左开右闭区间 (m, m+1]满足端点数据信息DI′：左端点小于S的一切元素而右端点不全小于S的一切元素.然后十等分 (m, m+1]得十进制数码m₁使半开区间 (m.m₁, m.m₁+10^-1]满足端点信息DI′；依次不断地十等分在前一步骤中所得的半开区间，得到无限十进制数码序列m₁, m₂, …, m_k，…, 每个数码m_k使得半开区间 (m.m₁m₂…m_k, m.m₁m₂…m_k+10^-k]满足端点信息DI′，从而得到一个无限小数m.m₁m₂…m_k-1m_k…，记为ξ；接着证ξ=inf S，先证ξ为S的下界，再证β>ξ不再是S的下界.

3 定理1的证法的统一探究——无限小数的不足近似和过剩近似的规定引起的一些瑕疵

教材[1]是通过反对称的方式规定正实数x= a₀.a₁a₂…a_n…和负实数y=-x=-a₀.a₁a₂…a_n…的n位不足近似和n位过剩近似的，即y_n=-x_n=-a₀.a₁a₂…a_n，y_n=-x_n=-a₀.a₁a₂…a_n-10^-n，这虽然比较自然便利，但在构造无限小数论证确界存在时就难以做到统一，这点从上述引申问题Q1~Q3的提示中不难发现.这不仅让教者和初学者期盼能否有一种统一的证法呢？

答案是肯定的，只需要给出无限小数一种特殊的约定.最好的做法是利用取整函数对无限小数表示的实数统一表示成x=[x]+{x}，其中取整函数[x]表示不超过x的最大整数，{x}=x-[x]表示x的非负小数部分.这时任何实数x，不管正数还是负数，x的n位不足近似和n位过剩近似主要由x的非负小数部分{x}相应的n位不足近似和n位过剩近似来确定，如x_n=[x]+{x}_n，x_n=[x]+$\overline{{{\left\{ x \right\}}_{n}}}$=x_n+10^-n.比如负实数y=-a₀.a₁a₂…a_n…的n位不足近似和n位过剩近似分别为

y_n=-(a₀+1)+(1-a₁a₂…a_n), y_n=-(a₀+1)+(1-a₁a₂…a_n+10^-n).

利用这个新约定，重新论证定理1，可以不必介意S是否含有非负数还是非正数，具体证明过程与上述证法没有实质性差异，在此省略.不过要注意的是，证明上确界的存在采用左闭右开区间[n₀, n₀+1) 不过为…, [-2, -1), [-1, 0), [0, 1), [1, 2), …之一，即这里n₀可以是负整数、零和正整数，依次十等分得到的10^k分位数码n_k使得半开区间[n₀+ 0.n₁n₂…n_k, n₀+0.n₁n₂…n_k+10^-k) 满足上述提及的端点信息DI；而证明下确界的存在上确界采用左开右闭区间 (n₀, n₀+1]的十等分法来构造作为准下确界的无限小数，依次十等分得到的10^k分位数码n_k使得半开区间 (n₀+0.n₁n₂…n_k, n₀+0.n₁n₂…n_k+10^-k]满足上述提及的端点信息DI′.