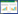文章信息
- 范飞飞
- FAN Fei-fei
- 西部地区经济增长差异分析模型构建
- An Analysis Model of Economic Growth Difference in Western China
- 广西民族大学学报(自然科学版), 2017, 23(4): 64-68
- Journal of Guangxi University for Nationalities(Natural Science Edition), 2017, 23(4): 64-68
-
文章历史
- 收稿日期: 2017-09-10
自国家推行西部大开发政策以来, 我国各个省市和自治区的经济均有了突飞猛进的发展, 西部各省份人民的生活水平也有了显著提高, 西部各省区经济也得到了快速发展[1].这主要表现在地区经济实力明显增强, 农业、工业、服务业三个产业的产业结构也日趋呈现合理化和高级化的趋势, 居民生活水平也有较大幅度的提高.但是在社会总产值, 服务业占该地区生产总值(GDP)等综合体现发展情况的各个因子上[2], 与我国的中东部各个省份尤其是江苏、浙江、广州等沿海省份相比仍然存在一定差距.此外, 西部地区份各省的经济统计指标也呈现出十分巨大的差别.
本文选取西部各省份的人均生产总值作为反映经济增长差异性的指标[3], 以及综合有关文献的研究, 本文选取4项经济统计指标以反映西部各省份经济发展水平, 即各省份的地区生产总值(X1)、人均地区生产总值(X2)、固定资产投资金额(X3)、居民消费价格指数(X4), 将各个指标表示为R=(R1, R2, R3, R4)[4].样本集用P表示, 样本对象为西部地区12个省和自治区, 即蒙、桂、渝、川、贵、云、藏、陕、甘、青、宁、新12个省市和自治区, 分别表示为P1, P2, P3, P4, P5, P6, P7, P8, P9, P10, P11, P12.
数据挖掘技术在20世纪80年代形成, 对其研究在20世纪90年代以来得到了突飞猛进的进展[5].数据挖掘是一种需求和数据在一起的方式.目前, 数据挖掘技术正在成为我国大数据和网络中的一个新的运用趋势.数据挖掘可以有效地降低管理成本, 实现过去所不能实现的功能.由于其功能完备, 方法较多, 下属的模型十分丰富, 数据挖掘技术正在被越来越多的学术和商业分析使用者所应用[6], 可以帮助知识使用者对信息进行深度处理的需求, 有利于快速决策, 精准决策以及提高决策质量.当前, 数据挖掘的功能包括对数据挖掘含义的理解、概念划分等十分强大的功能.数据挖掘对信息的处理效果主要分为两类:描述和预测.描述主要是对所处理的信息源的一般规律的分析; 预测是对给定的数据进行分析的基础上, 结合所研究问题的现状预测事物未来的发展规律.
目前, 国内许多学者、高等院校、科研单位都在积极开展对数据挖掘技术的研究, 有些对现有的关联规则算法进行改造和优化, 也有些在探索Web数据和非结构型数据的挖掘.
若研究蒙桂渝川贵等省份的差异化水平与各个统计因子之间的关系, 可采用《中国统计年鉴》中的统计数据进行分析以提高数据挖掘的精确性, 从数据源范围来看, 将西部12省份的数据全部纳入分析范围.对蒙桂渝川贵等各个省份的数据分别进行数据挖掘分析, 寻找统计数据与数据挖掘的结果的联系与区别.此文采用数据挖掘中的决策树模型探讨蒙桂渝川贵等地区的经济增长的差异性, 并在此基础上分析数据挖掘技术和传统的统计方法的联系和区别.
1 决策树模型在决策树构建的过程中, 我们通过信息熵确定每次数据划分所带来的收益, 其公式如下:
| $ \text{Entropy}=-p\text{log}\left( p \right)-\left( 1-p \right)\text{log}\left( 1-p \right) $ | (1) |
其中p为当前节点中右侧样本的比例, 所谓右侧样本, 是指样本值与均值的样本, Entropy越大, 说明节点的样本越分散, 即样本方差越大, 因此研究中希望Entropy尽可能小.假设我们每次对数据划分均采用二分法, 分别为左侧(left)和右侧(right), 左侧是指样本值小于均值的点, 右侧是指样本值大于均值的点, 进行分化后的收益就是分化前节点的取值减去这两个节点的期望值.即:
Entropy(parent)-Prob(left)×Entropy(left)+Prob(right)×Entropy(right),
这个值越大越好.这个收益, 学术上我们称作"信息增益".其中Prob(left)为左节点的样本比例, Prob(right)为右节点的样本比例.式(1)的推导过程如下:
采用二分类对问题进行研究时, 即样本中只有两类样本:左侧样本(样本值小于均值的点), 右侧样本(样本值大于均值的点).将第i个样本带入式(1)中可以得到:
| $ {L_i} = p_i^{y_i}{\left( {1 - p_i} \right)^{1 - y_i}} $ | (2) |
其中:yi表示第i个样本的类标签, 即当假设样本的概率服从参数为B(1, pi)的二项分布, 每个样本独立同分布, 也就是该问题的目标函数可表示为:
| $ {\text{Loss}} = \mathop \prod \limits_{i = 1}^n [p_i^{y_i}{(1-{p_i})^{1-y_i}}] $ | (3) |
构造函数f=-log(Loss)
| $ = - 1.0 \cdot \sum\limits_{i = 1}^n {\left[{{y_i}{\text{log}}\left( {{p_i}} \right) + \left( {1-{y_i}} \right){\text{log}}\left( {1-{p_i}} \right)} \right]} $ | (4) |
函数f关于其参数pi∈(0, 1)的二阶导数大于0恒成立, 说明函数f有且只有一个极小值点, 且为凸函数, 欲求得pi的值, 可令其一阶导数为0.
根据决策树模型, 可以求得式(4)中的一阶导数值
| $ \begin{array}{l} \frac{{\partial f}}{{\partial {p_k}}} = - \sum\limits_{i = 1}^m {\left[{\frac{{{y_i}}}{{{p_k}}}-\frac{{1-{y_i}}}{{1-{p_k}}}} \right]} \\ \;\;\;\;\;\; = \sum\limits_{i = 1}^m {\frac{{1 - {y_i}}}{{1 - {p_k}}}} - \sum\limits_{i = 1}^m {\frac{{{y_i}}}{{{p_k}}} = 0} \end{array} $ |
化简为:
| $ \text{求得:}{{p}_{k}}=\frac{\sum\limits_{i=1}^{m}{{{y}_{i}}}}{\sum\limits_{i=1}^{m}{{{y}_{i}}}+\sum\limits_{i=1}^{m}{\left( 1-{{y}_{i}} \right)}}=\frac{\sum\limits_{i=1}^{m}{{{y}_{i}}}}{m} $ | (5) |
其中:m为该节点样本总数, 分式的分子取值为样本值大于均值的点个数, 则pk即为该种群中右侧节点占总节点数的比例.将pk带入公式得到:
| $ {{f_k}}={\sum\limits_{i = 1}^m {{y_i}{\text{log}}\left( {{p_k}} \right)} - \sum\limits_{i = 1}^m {\left( {1 - {y_i}} \right){\text{log}}\left( {1 - {p_k}} \right)} } $ |
使用节点样本数对式(5)中的结果进行归一化处理后, 得到:
| $ \begin{array}{l} \frac{{{f_k}}}{m} = \frac{{\sum\limits_{i = 1}^m {{y_i}{\text{log}}\left( {{p_k}} \right)} + \sum\limits_{i = 1}^m {\left( {1 - {y_i}} \right){\text{log}}\left( {1 - {p_k}} \right)} }}{m}\\ \;\;\;\; = \frac{{\sum\limits_{i = 1}^m {{y_i}} }}{m}{\text{log}}\left( {{p_k}} \right) - \frac{{\sum\limits_{i = 1}^m {\left( {1 - {y_i}} \right)} }}{m}{\text{log}}\left( {1 - {p_k}} \right)\\ \;\;\;\; = p_i^{y_i}{(1 - {p_i})^{1 - y_i}} \end{array} $ |
即为式(1), 证明完毕.
2 数据来源及预处理本文根据2011年《中国统计年鉴》, 选取了主要反映蒙桂渝川贵等西部12个省市和自治区2010年的12个经济指标进行MATLAB分析, 得到影响经济发展水平的主要因素, 将数据输入MATLAB R2015a进行主成分分析, 由于各省份的地区GDP、固定资产投资总额、居民消费价格指数(CPI)三个因素对经济增长的影响情况较为显著, 因此选取这三个因子作为综合指标来反映经济发展水平.此外, 本文选取西部各省份的人均生产总值作为反映经济增长差异性的指标.2010年西部各省份的人均生产总值如表 1所示.
| 省份 | 人均GDP(元) | 排序 | 各省份 | 人均GDP(元) | 排序 |
| 内蒙古 | 47347 | 1 | 四川 | 21182 | 7 |
| 重庆 | 27596 | 2 | 广西 | 20219 | 8 |
| 陕西 | 27133 | 3 | 西藏 | 17027 | 9 |
| 宁夏 | 26860 | 4 | 甘肃 | 16113 | 10 |
| 新疆 | 25034 | 5 | 云南 | 15752 | 11 |
| 青海 | 24115 | 6 | 贵州 | 13119 | 12 |
| 注:西部省区平均人均生产总值为23458元 | |||||
人均国内生产总值(GDP)可以代表一个地区的经济发展的效率, 也是一个地区经济社会发展水平的客观反映, 由表 1可见, 西部地区经济发展差距较大, 人均GDP最高的内蒙古自治区远高于西部省份的平均水平.贵州人均国内生产总值最低.人均GDP最高省份是的最低省份的3.6倍.2010年蒙桂渝川贵等中国西部的12个省市和自治区的地区GDP、固定资产投资、CPI三个指标数据如表 2所示.
| 省份 | 地区生产总值 | 固定资产投资 | 居民消费价格指数 |
| 内蒙古 | 11672 | 8926.5 | 103.2 |
| 广西 | 9569.85 | 7057.6 | 103 |
| 重庆 | 7925.58 | 6688.9 | 103.2 |
| 四川 | 17185.48 | 13116.7 | 103.2 |
| 贵州 | 4602.16 | 3104.9 | 102.9 |
| 云南 | 7224.18 | 5528.7 | 103.7 |
| 西藏 | 507.46 | 462.7 | 102.2 |
| 陕西 | 10123.48 | 7963.7 | 104 |
| 甘肃 | 4120.75 | 3158.3 | 104.1 |
| 青海 | 1350.43 | 1016.9 | 105.4 |
| 宁夏 | 1689.65 | 1444.2 | 104.1 |
| 新疆 | 5437.47 | 3423.2 | 104.3 |
| 平均值 | 3832.72 | 5157.7 | 103.6 |
3 决策树算法的数据挖掘
决策树算法是基于分治法来解决分类问题, 通过为每个叶节点建立一个规则, 把从根节点到叶节点的路径中遇到的所有测试条件联合起来, 从决策树上可以简单快速的直接读出一组规则集成, 这是贪心算法的一种很重要的应用, 它不能保证最好的条件组合是否会被删除, 但在实际中却能产生相当好的规则集, 即使在实际问题中得不到问题的最优解, 也可以得到问题的满意解.
关于目标变量的分析, 这种判断可能需要一个算法:当一个或多个统计数值数据, 例如人均国内生产总值, 当这个值高于某一阈值时, 那么可以认为该地区的经济发展水平高于西部省份的平均概率的比例是相当大的, 这个过程可以尽可能简单快速的判断.那么, 对于实现这一目的, 决策树是一种有效的工具.如果我们能够建立一个有关的经济发展差异性分析决策树, 树的根节点将在顶部判断每一个统计数据的大小, 可以得出某一个省市和自治区的区域经济发展水平是否好于西部省份平均水平的结论.
从分化的经济增长水平的实际情况出发, 如果想判断经济发展水平和各种统计因子之间的关系, 往往需要十分复杂的模型和反复的计算和验证, 如果可以添加一个目标变量如人均GDP, 那么可以将所研究的问题进行简化.首先将西部12省份人均GDP相加, 再除以省份数, 即可计算出其算术平均值, 然后用每个省的人均GDP比西部人均地区生产总值的平均水平进行比较, 可以得到每个省的人均地区生产总值是否高于西部地区生产总值的结论, 根据每个省人均GDP与西部平均GDP之间的差别的将其值分为4个部分, 即X>0.2是非常高, 说明该地区的经济发展十分好; 0.01 < X < 0.2为较高, 说明该地区的经济发展较好, -0.2 < X < -0.01为较低, 说明该地区的经济发展较为一般; X < -0.2为非常低, 说明该地区的经济发展很差, 远远低于平均水平.
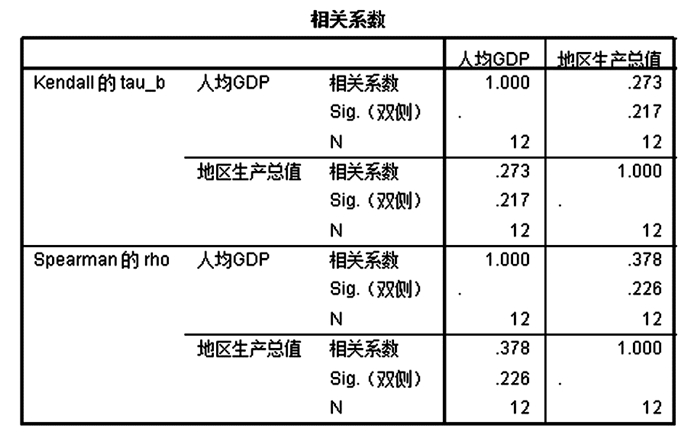
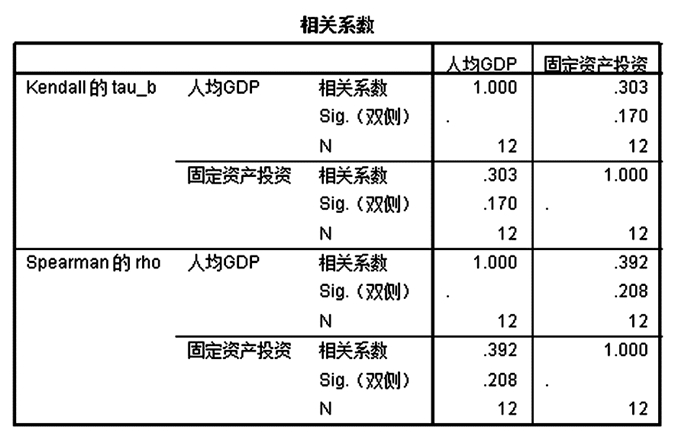
首先通过SPSS软件中的关联度分析模块对人均生产总值和地区生产总值(GDP)、固定资产投资、居民消费价格指数(CPI)三个因素进行相关性分析, 其结果如图 1~图 3所示.
|
| 图 1 相关性分析(1) Fig. 1 Correlation analysis(Part Ⅰ) |
|
| 图 2 相关性分析(2) Fig. 2 Correlation analysis(Part Ⅱ) |
|
| 图 3 相关性分析(3) Fig. 3 Correlation analysis(Part Ⅲ) |
从图 1~图 3可以看出, 人均生产总值与地区生产总值、固定资产投资、居民消费价格指数三个指标之间均存在一定的正相关关系, 且相关性不是十分显著, 且与三个指标的相关性程度接近, 所以要进一步通关决策树方法判断人均生产总值与三个因素间关系.当采用CRT方法进行增长时, 结果如图 4所示.
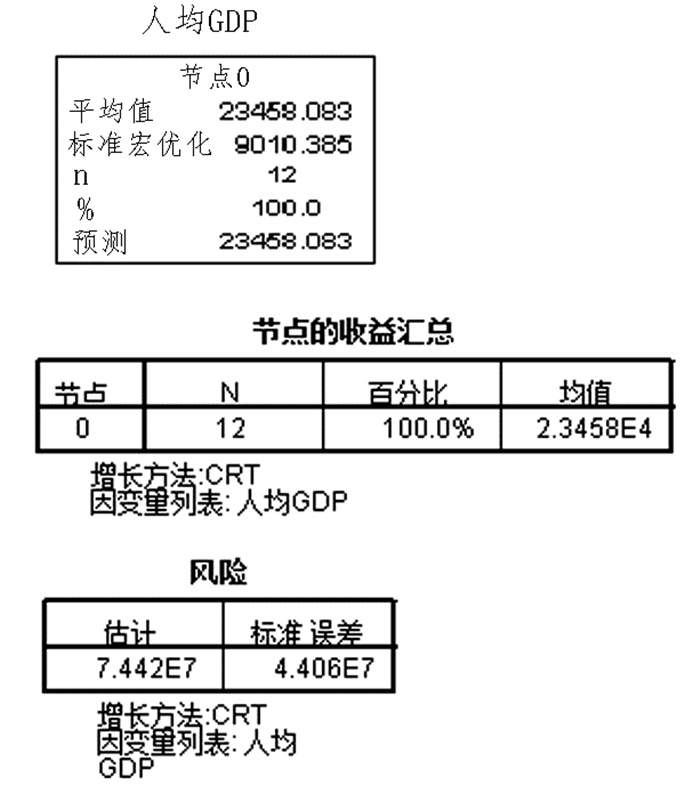
|
| 图 4 CRT方法增长时的决策树分析 Fig. 4 Decision Tree Analysis on the Growth of CRT Method |
通过SPSS中的决策树方法进行计算, 对结果汇总得出西部各省区的人均生产总值、地区生产总值、固定资产投资、居民消费价格指数关系如表 3所示.
| 名称 | 人均生产总值是否高于平均水平 | 地区生产总值是否高于平均水平 | 固定资产投资是否高于平均水平 | 消费价格指数是否高于平均水平 |
| 内蒙古 | 是 | 是 | 是 | 否 |
| 广西 | 否 | 是 | 是 | 否 |
| 重庆 | 是 | 是 | 是 | 否 |
| 四川 | 否 | 是 | 是 | 否 |
| 贵州 | 否 | 是 | 否 | 否 |
| 云南 | 否 | 是 | 是 | 是 |
| 西藏 | 否 | 否 | 否 | 否 |
| 陕西 | 是 | 是 | 是 | 是 |
| 甘肃 | 否 | 是 | 否 | 是 |
| 青海 | 是 | 否 | 否 | 是 |
| 宁夏 | 是 | 否 | 否 | 是 |
| 新疆 | 是 | 是 | 否 | 是 |
传统的统计分析的方法对表 3中的数据进行研究时, 并不能得到有效的结论, 这是因为每一个统计因子与目标变量并没有呈现出强烈的相关关系, 仅仅通过统计分析无法得出有效的结论.对表 3数据分析可以得出, 居民消费价格指数可以很好地反映出西部各省份的经济发展差异化水平, 居民消费价格指数与人均生产总值的趋势呈现出一致性的概率为75%, 注意, 固定资产投资水平与经济增长出现不一致的概率是58%, 目前GDP与经济发展不一致的概率是58%, 可见, GDP和固定资产投资水平说明的经济发展水平相近, 与上述两个因素相比, 居民消费价格指数更能反映出西部各省份经济发展的差异化水平.
从数据挖掘的角度来看, 有必要分析超过一年的数据, 并建立更多的决策树才能更快速、更准确地找到经济增长差异化和各个统计指标之间的关系.如果只有一年的数据建模和分析, 还不能构成一个完整的数据挖掘过程, 还需要建立模型来验证和预测未来的数据, 并检验模型的有效性.考虑到经济增长的相似性, 可以构建决策树使用相邻两年中前一年的数据, 然后使用决策树后一年的数据预测和验证, 精度测试的决策树预测.下一步可做这项研究.
4 结论本文基于2010年相关统计数据, 采用数据挖掘的决策树方法进行分析, 找到了反映西部各省份经济增长差异化水平的初步规律, 即居民消费价格指数与人均生产总值的相似程度最大, 最能代表西部各省份经济发展的差异化水平.虽然本文数据挖掘的数据源规模有限, 但是也可以针对研究提出政策性建议.如果要体现地区发展的差异化水平, 可以从以下几个方面入手:
一是扩大数据源, 本文中只采用地区生产总值、固定资产投资、居民消费价格指数(CPI)作为输入变量, 此外, 还可以采用各种宏观经济数据进行数据挖掘分析, 如地方财政一般预算收入、地方财政一般预算支出、对外贸易、社会消费品零售总额、消费价格指数、城镇居民人均消费支出, 城镇居民人均可支配收入、第一产业增加值、职工工资总额, 甚至地方政府管理理念的量化指标作为输入变量, 从一个更广泛的经济增长分化的影响因素进行探索.
二是可以选择更多的时间跨度的信息和数据进行分析, 因为不同时间的数据反映出不同问题的特征, 且多时间跨度的信息还可以反映出问题的动态变化规律, 注意, 此时需要通过数据转换实现不同年度的数据前后口径的统一, 提高分析的准确性.
三是可以对决策树算法进行更深一步的分析和研究, 对其进行建模分析, 以对问题进行深入的研究.此外, 还可以采用其他算法, 如聚类分析等, 以及综合多种算法进而对问题进行更深一步的研究, 更好的验证文章的结论.
| [1] | 韦艳玲, 廖燕玲. 西部各省区经济发展的状况评价与对策——基于因子分析法的实证分析[J]. 柳州职业技术学院学报, 2008, 8(2): 7–10. |
| [2] | 田萍, 武新乾, 梅倩倩, 等. 我国城乡居民消费与经济增长区域差异性的实证分析[J]. 数学的实践与认识, 2014(22): 89–95. |
| [3] | 赵丹妮. 广东省区域经济增长影响因素的空间计量分析[J]. 统计与决策, 2015(15): 101–104. |
| [4] | 韦艳玲, 李春贵. 数据挖掘技术在西部各省区经济发展状况分类中的应用[J]. 商场现代化, 2008(22): 59–60. DOI:10.3969/j.issn.1006-3102.2008.22.041. |
| [5] | 方永美, 孙凌洁, 廖鉴康, 等. 基于决策树算法的蔬菜农药残留的数据挖掘与分析[J]. 广东农业科学, 2014, 41(3): 194–197. |
| [6] | 朱鑫榕. 数据挖掘方法及其在我国财政管理领域的应用[J]. 经济问题, 2015(1): 64–68. |
 2017, Vol. 23
2017, Vol. 23