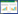文章信息
- 周序林, 张显成
- ZHOU Xu-lin, ZHANG Xian-cheng
- 张家山汉简《筭数书》体积算题及相关问题探析
- Analysis of Volume Chapters in Suànshù shū——the book of Mathematics and Related Issues
- 广西民族大学学报(自然科学版), 2017, 23(3): 22-27, 60
- Journal of Guangxi University for Nationalities(Natural Science Edition), 2017, 23(3): 22-27, 60
-
文章历史
- 收稿日期: 2017-03-03
2. 西南大学 汉语言文献研究所, 重庆 北碚 400175
2. The Institute of Chinese Language and Bibliography, the Southwest University, Beibei 400715, China
1983年12月到1984年1月,在湖北江陵县张家山第247号西汉早期墓葬出土的《筭数书》,是中国目前所见最早的算数书之一.该书未见文献记载,是一部亡佚两千多年的古数学书.这部书是一个数学问题集,一共有69个算题,可分为算术和几何两大类,其中几何类算题共16个,包括面积算题9个,体积算题7个.每一体积算题的内容,包括以下四个部分:
题名,即算题的名称,如“斩都”.体积算题的题名均采自题文的首句.
题文,即算题的已知条件,如“斬都下厚四尺,上厚二尺,高五尺,袤二丈”.紧随已知条件的是答案,没有出现提问.提问隐含在已知条件与答案之间,意为“问体积是多少?”
答案,即算题的计算结果,如“責(積)百卅三尺少半尺”.
解题方法,即按照法则求解的运算过程,且以“术曰”表示.如“术(術)曰:倍上厚,以下厚增之,以高及袤乘之,六成一”.
以上“题文”“答案”“解题方法”三部分在下文的解读中多译为现代汉语,以利于理解.
这里就这7个体积算题及相关问题进行分析讨论.体积算题的释文和对题意的解读主要参考张家山二四七号汉墓竹简整理小组《张家山汉墓竹简(二四七号汉墓)》(释文修订本)和彭浩《张家山汉简〈算数书〉注释》(科学出版社,2001年),不过,下文所出示的释文和对题意的解读,也时有我们自己的意见,除比较重要的以“按”说明外,不再一一说明.
下文释文采用的符号及含义如下:□,表示无法补出的残缺字,一“□”表示一字;
美〈羨〉除,其定(頂)方丈,高丈二尺,其除廣丈、袤三丈九尺,其一旁毋高,積三〈二〉千三百六〈四〉十尺.术〈術〉曰:廣積卅尺除〈乘〉高,以其141[廣]、袤乘之,【六而一】即定.142[3]266
题名:除
题文:美〈羨〉除,其定(頂)方丈,高丈二尺,其除廣丈、袤三丈九尺,其一旁毋高.
羡除的底座宽一丈,高一丈二尺,通道宽一丈,长三丈九尺,另一端无高.
答案:積三〈二〉千三百六〈四〉十尺.
体积是二千三百四十立方尺.
解题方法:术〈術〉曰:廣積卅尺除〈乘〉高,以其[廣]、袤乘之,【六而一】即定.
三宽之和(三十尺)乘以高,乘以长,除以六.
计算公式:V= (a+b+c)hL÷6
即:V=(10+10+10)×12×39÷6(单位:尺) =2340(立方尺)
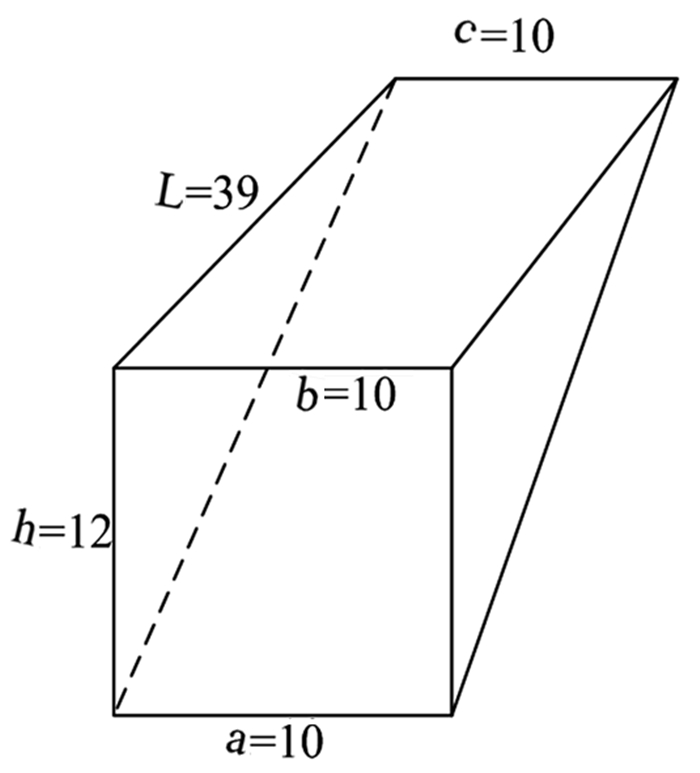
1.2 斬都斬都下厚四尺,上厚二尺,高五尺,袤二丈,責(積)百卅三尺少半尺.术(術)曰:倍上厚,以下厚增之,以高及袤乘之,六成一.143[5]151
题名:斬都
题文:斬都下厚四尺,上厚二尺,高五尺,袤二丈.
斩都下宽四尺,上宽二尺,高五尺,长二丈.
答案:責(積)百卅三尺少半尺.
体积一百三十三又三分之一立方尺.
解题方法:术(術)曰:倍上厚,以下厚增之,以高及袤乘之,六成一.
上宽乘以二加下宽,之和乘以高与长,除以六.
如图 2:
|
| 图 2 斩都 Fig. 2 Geometric figure of Zhǎndū斬都 (a为下宽,b为上宽,h为高,L为长.单位:尺) Chopping a short wooden stake |
计算公式:V=(2b+a)hL÷6
即:V= (2×2+4)×5×20÷6(单位:尺) =133(立方尺)
按:张家山二四七号汉墓竹简整理小组《张家山汉墓竹简(二四七号汉墓)》(释文修订本)和彭浩《张家山汉简〈算数书〉注释》,以及学界对“斩都”几何图形的解读和题名的解读均不确,关于题名的解读,详见下文,关于几何图形的解读,我们将另文专论.
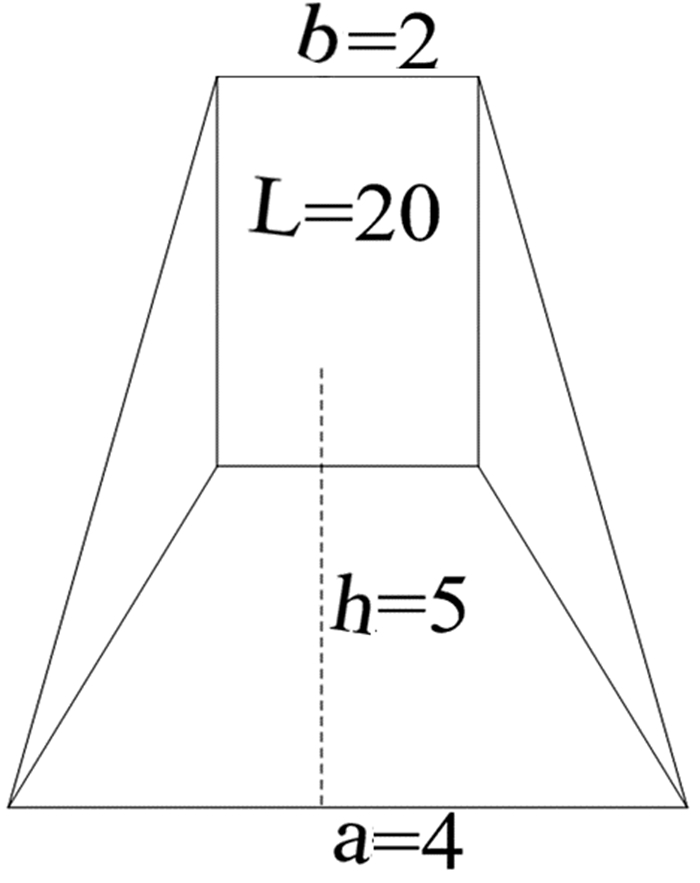
1.3 芻芻童及方闕下廣丈五尺、袤三丈,上廣二丈、袤四丈,高丈五尺,積九千二百五十尺.术(術)曰:上廣袤、下廣袤各自乘,又上144袤從下袤以乘上廣,下袤從上袤以乘下廣,皆並,【以高】[6]67乘之,六成一.145[5]151
题名:芻
题文:芻童及方闕下廣丈五尺、袤三丈,上廣二丈、袤四丈,高丈五尺.
刍童及方阙的下底面宽一丈五尺、长三丈,上底面宽二丈、长四丈,高一丈五尺.
答案:積九千二百五十尺.
体积为九千二百五十立方尺.
解题方法:术(術)曰:上廣袤、下廣袤各自乘,又上袤從下袤以乘上廣,下袤從上袤以乘下廣,皆並,【以高】乘之,六成一.
上底面的长宽相乘,下底面的长宽相乘,上下底面长之和乘以上底面宽,上下底面长之和乘以下底面宽,以上各得数相加之和乘以高,除以六.
如图 3:
|
| 图 3 刍 Fig. 3 Geometric figure of Chú芻Hay stack (a为上底面长,b为上底面宽,c为下底面长,d为下底面宽,h为高.单位:尺) |
计算公式:V=[ab+cd+(a+c)b+(c+a)d]h÷6
即:V=[40×20+30×15+(40+30)×20+(30+40)×15]×15÷6(单位:尺) =9250(立方尺)
1.4 旋粟旋粟高五尺,下周三丈,積百廿五尺.·[4]105二尺七寸而一石,為粟
题名:旋粟
题文:旋粟高五尺,下周三丈.
旋粟的高五尺,周长三丈.
答案:積百廿五尺.·二尺七寸而一石,為粟
体积是一百二十五立方尺.二立方尺七立方寸粟为一石,该旋粟为四十六又二十七分之八石.
解题方法:其述(術)曰:下周自乘,以高乘之,卅六成一.·大積四千五百尺.
周长乘以周长, 乘以高,除以三十六.以周长为边长的长方体体积是四千五百立方尺.
如图 4:
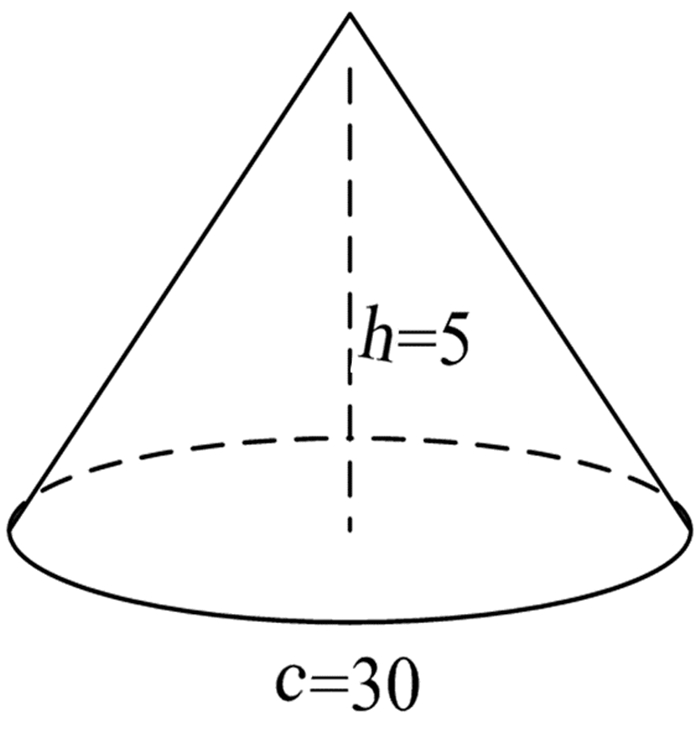
|
| 图 4 旋粟 Fig. 4 Geometric figure of Xuánsù旋粟Conical millet stack (c为周长,h为高.单位:尺) |
计算公式:V=c2h÷36
即:V=30×30×5÷36(单位:尺) =125(立方尺)
1.5 囷蓋囷蓋下周六丈,高二丈,為積尺二千尺,乘之=(之)[4]107述(術)曰:直(置)如其周令相乘也∠[4]107,有(又)以高乘之,卅六成一.148[5]152
题名:囷蓋
题文:囷蓋下周六丈,高二丈
囷盖的周长六丈,高二丈.
答案:為積尺二千尺
体积是二千立方尺.
解题方法:乘之=(之)述(術)曰:直(置)如其周令相乘也∠,有(又)以高乘之,卅六成一.
周长乘以周长,乘以高,除以三十六.
如图 4:
计算公式:V=c2h÷36(c为周长,h为高)
即:V=60×60×20÷36(单位:尺) =2000(立方尺)
1.6 睘(圜)亭圜亭上周三丈,大〈下〉周四丈,高二丈,積二千五十五尺卅六分尺廿.術曰:下周乘上周=,(周)[4]107自乘,皆並,以高149乘之,卅六成【一】.今二千五十五尺【卅六】分【尺】廿.150[5]152
题名:圜亭
题文:圜亭上周三丈,大〈下〉周四丈,高二丈
圆亭的上周长三丈,下周长四丈,高二丈.
答案:積二千五十五尺卅六分尺廿
体积是二千零五十五又三十六分之二十立方尺.
解题方法:術曰:下周乘上周=,(周)自乘,皆並,以高乘之,卅六成【一】.今二千五十五尺【卅六】分【尺】廿.
下周长乘以上周长,下周长乘以下周长,上周长乘以上周长,三个得数之和乘以高,除以三十六,即得二千零五十五又三十六分之二十立方尺.
如图 5:
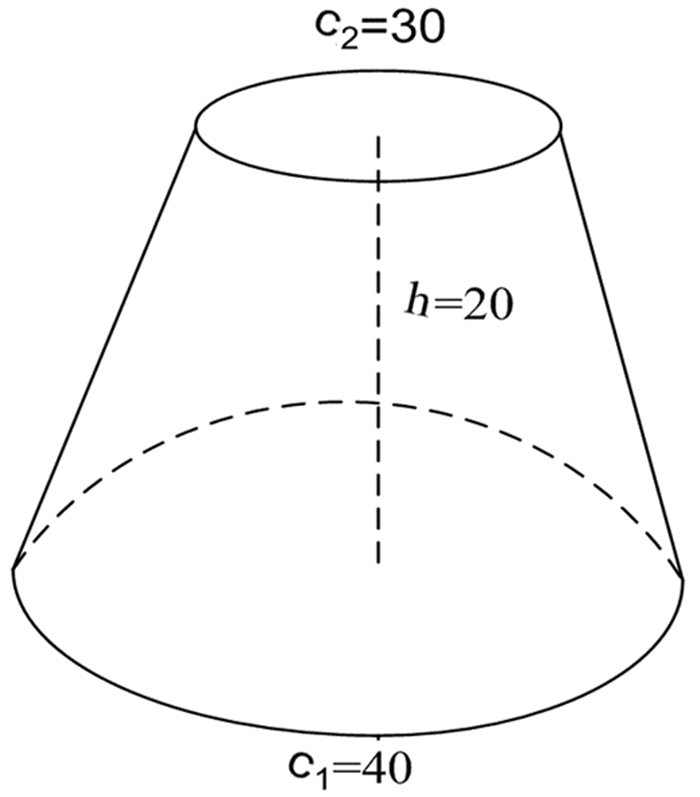
|
| 图 5 圆亭 Fig. 5 Geometric figure of Yuántíng圆亭Round pavilion (c1为下周长,c2为上周长,h为高.单位:尺) |
计算公式:V=(c1×c2+c12+c22)h÷36
即:V= (40×30+40×40+30×30)× 20÷36(单位:尺)
=
圜材、井、窌若它物,周二丈四尺∠,深丈五尺∠,積七百廿尺.術曰:耤(藉)周自乘,以深乘之,十二成一∠[4]109.一曰以151
题名:井材
题文:圜材、井、窌若它物,周二丈四尺∠,深丈五尺∠.
圆木、井、地窖等物体,周长二丈四尺,深一丈五尺.
答案:積七百廿尺.
体积为720立方尺.
解题方法:術曰:耤(藉)周自乘,以深乘之,十二成一∠.一曰以
周长乘以周长,乘以深,除以十二;另一方法:周长乘以直径,除以四.
(注:小黑点·后的简文疑为下一章开始,且简文损毁严重,不知其意,故不译.)
如图 6:
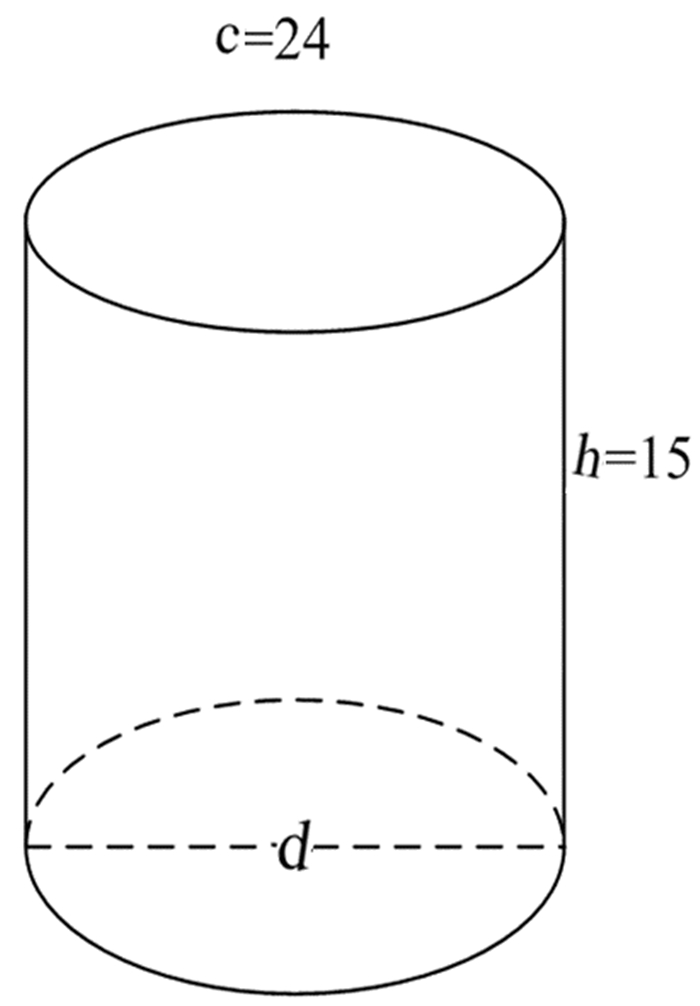
|
| 图 6 井材 Fig. 6 Geometric figure of Jǐngcái井材Well & timber (c为周长,d为直径,h为深.单位:尺) |
解题方法一
计算公式:V=c2h÷12
即:V=24×24×15÷12(单位:尺) =720(立方尺)
解题方法二
计算公式为:V=c×d ÷4
(按:V=2πr×2r÷4=πr2,这是计算底面积的算法.显然,简文书写者有意省略了与前文相同的一个要素,即“以深乘之”.计算公式应为:V=c×d×h)
即:
《筭数书》体积算题成题时代应该是春秋晚期至公元前186年闰九月或其后不久.
证据一:与《筭数书》共存于第247号汉墓的是一份历谱,它是整个第247号墓竹简断代的主要依据,其记录的最后一年是吕后二年后九月[5]4,即公元前186年闰九月,墓主去世当在西汉吕后二年(公元前186年)闰九月或其后不久[2]95.可以认定《筭数书》体积算题成题年代的下限为公元前186年闰九月或其后不久.
证据二:据雍城考古队《陕西凤翔高庄秦墓地发掘简报》,囷,俗称仓,此次发现三种形制的囷,它们除了有圆形的仓体外还有一个共同的特征,即仓顶盖有出檐圆攒尖顶[7]16.
囷盖就是这种仓库的顶盖,呈正圆锥形.彭浩先生指出,这种带正圆锥形仓盖的囷最早在关中的秦墓中通过考古发现的,其年代可早到春秋晚期,然后秦人在征战统一中国的过程中,传播到关东各地,到西汉中期汉武帝前后,代之以无盖的直筒形圆仓[8]85 .因此我们也许可以说“囷盖”算题应该是秦人的作品,成题时代或许可以追溯到春秋晚期.
旁证一:通读《筭数书》发现战国时期的秦律在书中体现得十分普遍,故《筭数书》的主体应该是形成于战国时代.例如,1975年12月在湖北省孝感地区云梦县睡虎地11号秦墓出土的“睡虎地秦简”,记载的主要内容是公元前217以前的秦国法律条文和文书,其《秦律十八种》之《仓律》与《筭数书》记载的一段秦律内容高度吻合:
《仓律》:【粟一】石六斗大半斗,舂之為(糲)米一石;(糲)米一石為糳米九斗;九【斗】為毀(毇)米八斗.稻禾一石, ……倉42為粟廿斗,舂為米十斗;十斗粲,毀(毇)米六斗大半斗.麥十斗,為三斗.叔(菽)、荅、麻十五斗為一石.·稟毀(毇)粺者, 以十斗為石.倉43[9]29-30
《筭数书》:禾程程曰:禾黍一石為粟十六斗泰(大)半斗, 舂之為米一石, 米一石為糳米九斗, 糳米【九】斗為毀(毇)米八斗.王88程曰:稻禾一石為粟廿斗,舂之為米十斗為毀(毇), 粲米六斗泰(大)半斗.麥十斗【為】三斗.89程曰:麥、菽、荅、麻十五斗一石, 稟毀(毇)糳者,以十斗為一石.90[5]144
旁证二:根据邹大海先生《睡虎地秦简与先秦数学》的研究,秦法律比过去任何时代都要严苛[10]57-65.秦律《效律》对会计、统计工作的要求非常严格[9]67-77;《秦律十八种》之《徭律》规定,工程质量出了问题要追究官吏和施工方责任,工程量估算出了问题,要对负责估算的官吏和匠人进行处罚[9]47-49.这些情况说明先秦时代既对体积计算有大量需求,又掌握了相应的计算方法,为体积算题的产生提供了社会条件.
2.2 算题目的正如钱宝琮先生在《中国数学史·序》中所指:“中国数学发展的历史表明,我国历代的数学家不仅在算术和代数的许多方面有着杰出的成就,而且这些成就大多是能与实际需要相结合的[11].”春秋末以后,农业生产和手工业的技术都有了大的发展,人们的数学知识应有不断地提高.政府为了储备粮食,应有计算仓库容积的方法,要修建灌溉管道、治水的堤防和其他土木工事,必须能计算工程人工.体积算题当是利用当时几何学知识,结合社会实际需要进行应用的结果,注重于实际应用,满足老百姓日常生活中遇到的体积计算问题,满足政府官吏在日常管理工作中需要解决的体积问题,并为解决实际的体积计算问题提供实例.比如,《效律》和《秦律十八种》之《仓律》对政府仓储有严格规定,“刍”“旋粟”“囷盖”就是为了解决政府因征收大量实物田租和刍稿而进行的仓储管理中遇到的体积计算问题.再如“旋粟”中“二尺七寸而一石,为粟卌六石廿七分石之八”这一体积与重量的换算,用一种简便的方法有效地解决了大容量仓库称重这一费时费力的难题.根据《秦律十八种》,县级政府负责辖内各类工程修建和维护,“除”“斩都”“圆亭”和“井材”就是解决这些工程中体积计算的问题.总之,体积算题的目的是为基层吏民在管理和生活中对体积计算的实际需要服务的.
2.3 算题命名题名“除”.《说文·
题名“斩都”.斩,《说文·车部》:“也.”段玉裁注:“者,断也.……本谓斩人.引申为凡绝之称[12]730.”即本指斩人,泛指砍或砍断,如《周礼·考工记·轮人》:“轮人为轮,斩三材必以其时.”
都,有“橛”义,即“短木桩、木橛子”类义,此义最早是个方言词.《方言》卷五说:“橛,燕之东北朝鲜洌水之间谓之椴.”即“橛”在燕之东北朝鲜洌水之间叫“椴”.郭璞注释说道:“椴,楬杙也,江东呼都.”即“椴”在江东一带称作“都”.《广雅·释宫》说:“椴,杙也.”,即“椴”就是“杙”.王念孙疏证解释说:“椴之言段也,今人言木一段两段是也.”即“椴”得名于“段”,今人说木料截为一段两段的“段”正是这意思.也就是说,凡是木材形状截为短直的都叫“橛”[15]389-391.正如郭璞所说,“椴”在江东一带呼作“都”,而张家山汉简《算数书》的出土地点正属于“江东”楚方言区,从此点上讲,释“都”为“橛”正与郭璞注释相合.
斩都,即斩削短木桩、砍削木橛子,《筭数书》中的算题“斩都”一名自然指砍削短木桩、木橛子而成的楔形,并特指砍削木桩而成的楔口向下、楔口的长度大于与之平行的楔座边的长度的楔形(属非标准楔形).通过以上对该题内容的分析可知,“斩都”所指的几何图形正是这种图形,见图 2.
题名“刍”.此题名实际上涉及“刍童”和“方阙”两个概念,题名和紧接着的下文为“芻童及方闕下廣丈五尺”,故有必要对“刍童”和“方阙”意义进行解释.“刍”是“刍童”的省称,“刍童”疑为大名冠小名现象(注:大名冠小名是上古汉语的一个重要现象,即表示事物总称的语素在前,表示事物具体特点的语素在后,由两个语素组成的复音词).“刍”指牲口吃的草,如《庄子·列御寇》:“衣以文绣,食以刍叔[16]463.”此处指草堆;“童”指牛羊未长角或无角者,如《诗经·大雅·抑》:“彼童而角,实虹小子.”毛传:“童,羊之无角者也[17]266.”引申为上端无尖角的物体.“刍童”即“童刍”,指上端无尖角的草堆,此处指上底面和下底面都是长方形的台体[4]104.“阙”,《说文·门部》:“阙,门观也[12]588.”即古代宫殿门外两边的楼台,为台体.方阙与刍童相似,也是长方台体[4]104.皆见图 3.
题名“旋粟”.“旋”,圆.《庄子·达生》:“工倕旋而盖规矩.”[16]262陆德明释文:“旋,圆也.” [18]386旋粟是粟米堆积在地面上呈正圆锥体形状,指正圆锥体[4]106.见图 4.
题名“囷盖”.囷是古代一种圆形的粮仓,见图 7.囷盖是这种粮仓的盖,指正圆锥体.见图 4.
题名“圆亭”.圆亭是正圆形的亭台,指正圆台体,见图 5.
题名“井材”.井材,即井和木材;窌,地窖[12]345.圆材、井、地窖皆为呈圆柱体形状的物体,指圆柱体,见图 6.
这些章题都是以所求体积的实物命名,从侧面反映了中国早期几何注重实用性的特征.
2.4 数学成就论证几何学是古希腊数学的主要特征,讨论形的性质,偏重对定理的逻辑推理,依靠公理、公设而不是数量来进行几何证明,走的是理论几何学的道路.古代中国几何则不然,虽然在战国时代的《墨经》等著作中有过理论几何学的某种萌芽,如对“点”“平行”等概念的论证,但总体不是论证性的,而是直观的,主要探讨的是与测量有关的事实,这从所论7个体积算题可见一斑.这7个算题无一例外都是用具体物体命名,其直观性不言而喻;每个算题都侧重于几何体体积的计算而没有进行推理演绎,体现出我国古代数学重视数量计算,重视运用数学知识解决具体问题,这可能是由于我国古代数学源于生产实践而服务于生产实践的缘故.
另外,李约瑟在论及成书于公元1世纪的《九章算术》中“羡除”的体积公式时说:“库利奇(Coolidge)特别欣赏其中对斜截面三角柱体的处理,其公式相当于
可见,中国数学在战国时代的发展水平就已经很高,可以说是达到了一个高点.
| [1] | 张显成. 秦简逐字索引·凡例[M]. 成都: 四川大学出版社, 2010. |
| [2] | 张显成. 简帛文献学通论[M]. 北京: 中华书局, 2004. |
| [3] | 张家山二四七号汉墓竹简整理小组. 张家山汉墓竹简(二四七号汉墓)[M]. 北京: 文物出版社, 2001. |
| [4] | 彭浩. 张家山汉简《算数书》注释[M]. 北京: 科学出版社, 2001. |
| [5] | 张家山二四七号汉墓竹简整理小组. 张家山汉墓竹简(二四七号汉墓)(释文修订本)[M]. 北京: 文物出版社, 2006. |
| [6] | 胡忆涛. 张家山汉简《算数书》整理研究[D]. 西南大学, 2006. |
| [7] | 吴镇烽, 尚志儒. 陕西凤翔高庄秦墓地发掘简报[J]. 考古与文物, 1981(1). |
| [8] | 彭浩. 中国最早的数学著作《算数书》[J]. 文物, 2000(9). |
| [9] | 睡虎地秦墓竹简整理小组. 睡虎地秦墓竹简[M]. 北京: 文物出版社, 1990. |
| [10] | 邹大海. 睡虎地秦简与先秦数学[J]. 考古, 2005(6). |
| [11] | 钱宝琮. 中国数学史[M]. 北京: 科学出版社, 1964. |
| [12] | 段玉裁. 说文解字注[M]. 杭州: 浙江古籍出版社, 2006. |
| [13] | 司马迁. 史记[M]. 北京: 中华书局, 1959. |
| [14] | 黄冈市博物馆, 黄州区博物馆. 湖北黄冈两坐中型楚墓[J]. 考古学报, 2000(2). |
| [15] | 华学诚. 扬雄方言校释汇证[M]. 北京: 中华书局, 2006. |
| [16] | 王先谦撰, 陈凡整理. 庄子集解[M]. 西安: 三秦出版社, 2005. |
| [17] | 黄焯. 毛诗郑笺平议[M]. 武汉: 武汉大学出版社, 2008. |
| [18] | 陆德明撰. 经典释文[M]. 北京: 中华书局, 1983. |
| [19] | 李约瑟. 中国科学技术史·数学[M]. 北京: 科学出版社, 1978. |
 2017, Vol. 23
2017, Vol. 23