混杂系统 (Hybrid System，简称HS) 最早是在1986年在美国Santa Clara大学召开的高级控制会议被提出来，不久便成为计算机形式化理论研究的热点.经过十几年的发展，理论日趋完善. ^[1-5]混杂系统就是指同时存在相互作用的连续动态特性和离散事件特性的系统，^[2]其中离散部分在控制中常以调度程序或监控管理者的形式出现，譬如ON/OFF切换开关、阀门、传动装置、限幅器或者选择器，而连续部分则随着时间的推移不断演化. ^[6-7]随着计算机技术的发展和数字技术在各种类型的工业生产中的广泛应用，混杂系统大量出现，小的如化工蒸发系统、温度控制系统、液面控制系统、汽油泄漏检测系统等；大的如空中交通管理系统、机器人系统、汽车系统、智能高速公路系统等. ^[3-4]

近年来，混杂系统的研究已取得了初步结果，专家学者们从不同角度研究可达问题，对于不同的验证工具，可达集的表示也是多种多样，如UPPAL、KORONOS、Hypertech用超矩形表示可达集，Verishift用椭圆体表示可达集，Hyech、CheckMate和d/dt用多面体表示可达集. ^{[3, 7, 11]}可达集的表示方法对于整个验证精度有重要的作用. ^[13-14]一般地，选用何种表示方法需要考虑以下几个原则：计算复杂度、保守性大小、集合交并集处理能力和表示可达集所需的维数. ^[12]文中选择的是用多面体表示可达集，对混杂系统进行近似分析，^[15-16]首先用分割法求出多面体的近似体积，再与原体积相比较，最终算出所求的误差余项.

本文的组织结构为第一节主要介绍用分割法求近似多面体体积的理论和步骤，并举例分析；第二节根据混杂自动机的定义，再结合第一节分割法的原理，构造一个基于分割的近似混杂自动机，并证明二者的近似关系.

1 分割近似求解方法

本节中主要是关于用分割法求多面体体积的原理以及误差余项.

定义1  用P表示多面体，其代数表达式为

$ \{{{f}_{i}}={{a}_{1i}}{{x}_{1}}+\ldots +{{a}_{ni}}{{x}_{n}}+{{a}_{\left( n+1 \right)i}}=0\}, i\in \left[1, +\infty \right), n\in \left[2, +\infty \right). $

长方体是特殊的多面体，用B表示长方体，其代数表达式为f_i=a_ix+b_iy+c_iz+d_i=0，(i=1, …, 6).且长方体的体积计算公式为V_B=L×W×H(L =max{x}，W =max{W}，H =max{H})，L，W，H分别是长方体的长、宽、高.

定义2  将不规则多面体P分割成n个可计算的多面体P_i(i=1, …, n) 的方法称为分割法，其中S={P₁, …, P_n}为近似多面体，且任意多面体P_i都有一条边相等.通过映射关系得到S={P₁, …, P_n}$\underrightarrow{降维}$S′={P₁^′，…，P_n^′}，记为S=f(S′)，只需求出V_S′即可得出近似多面体S的近似体积V_S，与原多面体体积V_P有一定的误差，记为误差余项R=V_P-V_S.

下面介绍分割法中的降维步骤和分割法.

降维步骤：

由定义1得多面体P的表达式为$\overrightarrow{f\left( {\vec{x}} \right)}=0$，是n维的一个向量.

在二维平面，将多边形P分割成n个长方形F_i(i=1，…，n)，令F={F₁，…, F_n}，并且每个长方形的宽都相等W_Fi=△，即x∈{0, △, …, (n-1)△}，代入表达式得到n个长方形的长为L_Fi=f((i-1)△)，则面积为${{S}_{F}}=\sum\limits_{i=1}^{n}{{{S}_{{{F}_{i}}}}=}\sum\limits_{i=1}^{n}{{{L}_{{{F}_{i}}}}}\text{ }\!\!\times\!\!\text{ }{{W}_{{{F}_{i}}}}=\sum\limits_{i=1}^{n}{\Delta f\left( \left( i-1 \right)\Delta \right)}$.

在三维空间，将多面体P分割成n个长方体B_i=(i=1, …, n)，令B={B₁, …, B_n}，并且每个长方体的宽都相等W_Bi=△，即x∈{0, △, …, (n-1)△}，先将长方体B_i投影到二维xy平面上得到投影长方形B_i^′，根据二维平面上长方形的面积计算公式，可以得到$\sum\limits_{i=1}^{n}{{{S}_{B_{i}^{'}}}=}\sum\limits_{i=1}^{n}{\Delta f\left( \left( i-1 \right)\Delta \right)}$；然后计算长方体的高，即长方体B_i投影到二维xz平面上得到的投影长方形B_i^″的长，即H_Bi=L_Bi^″=f((i-1)△)；则体积为V_B=$\sum\limits_{i=1}^{n}{{{V}_{{{B}_{i}}}}=}\sum\limits_{i=1}^{n}{{{S}_{B_{i}^{'}}}\text{ }\!\!\times\!\!\text{ }{{H}_{{{B}_{i}}}}=}\sum\limits_{i=1}^{n}{\Delta {{f}^{2}}\left( \left( i-1 \right)\Delta \right)}$.

以此类推，在n维空间，将多面体P分割成n个多面体P_i(i=1, …, n)，令S={P₁, …, P_n}, 并且每个多面体的宽都相等W_Pi=△，即x∈{0, △, …, (n-1)△}，先将多面体P_i投影到n-1维空间得到投影多面体P_i^′，根据n-1维空间上的多面体计算公式，可以得到$\sum\limits_{i=1}^{n}{{{V}_{P_{i}^{'}}}}\sum\limits_{i=1}^{n}{\Delta {{f}^{n-2}}\left( \left( i-1 \right)\Delta \right)}$；然后计算多面体P_i的高，即多面体P_i投影到n-1维空间上得到的投影多面体P_i^″的高，再将多面体P_i^″投影到n-2维空间得到投影多面体P_i^'''，则多面体P_i^'''的高即为多面体P_i^″的高，然后依次投影，直到二维平面得到投影多边形P_i^(n-2)，则多边形P_i^(n-2)的长即为多面体P_i的高，即H_Pi=L_Pi^(n-2)=f((i-1)△)；则体积V_S=$\sum\limits_{i=1}^{n}{{{V}_{{{P}_{i}}}}=}\sum\limits_{i=1}^{n}{{{V}_{P_{i}^{'}}}\text{ }\!\!\times\!\!\text{ }{{H}_{{{P}_{i}}}}=}\sum\limits_{i=1}^{n}{\Delta {{f}^{n-1}}\left( \left( i-1 \right)\Delta \right)}$.

用分割法求近似多面体体积的算法如下：

1) Procedure

  Inputs:P;

  Output:V_S;

2) Begin

3)P$\underrightarrow{分割}\ $S={P₁，…，P_n}

 $\underrightarrow{降维}\ $S′={P₁^(n-2), …, P_n^(n-2)},

且W_P1=W_P2=…=W_Pn;

4) V_P1=V_P1^′×H_P1=V_P1^″ ×H_P1^′×H_P1 =V_P1^(n-2)×H_Pi^(n-3)×…×H_P1^′×H_P1;

V_P1^(n-2)=L_P1^(n-2)×W_P1^(n-2);

5) for (i=2; i < =n; i+ +)

6)V_Pi=V_Pi^′×H_Pi=V_Pi^″ ×H_Pi^′×H_Pi =V_Pi^(n-2)×H_Pi^(n-3)×…×H_Pi^′×H_Pi;

V_Pi^(n-2)=L_Pi^(n-2)×W_Pi^(n-2);

7) V_P=V_P1+V_Pi;

8) End

9) return V_S;

10) End Procedure

注：P表示多面体；V_S表示多面体S的体积；S是多面体P分割后的近似多面体；S′是多面体S降维后的近似多面体；L，W，H是多面体的长、宽、高.

引理1  对多面体分割过程中，将多面体P分割成n个多面体P_i(i=1, …, n)，令S={P₁, …, P_n}，则

1) 多面体P是多面体S的子集，记为P⊆S.即有V_P≤V_S.

2) 多面体S近似于多面体P.

证明：多面体P分割成n个多面体P_i(i=1, …, n)，令S={P₁, …, P_n}，可知多面体P中的任意一部分一定在近似多面体S内，显而易见，1), 2) 得证.

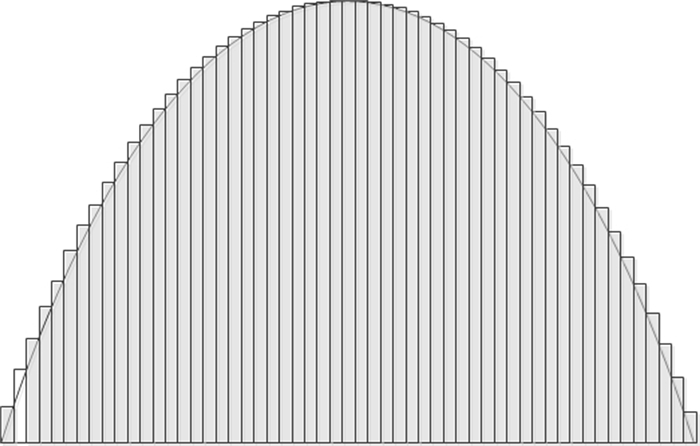
分割法是一种计算平面几何图形面积和体积的推导方法, 也是一种思考方法，可以将这种方法应用到实际的求解中，例如：图 1是将不规则的多边形P分割成n个规则的长方形的示意图，分割成的长方形分别为A_i(i=1, …, n)，并且长方形的宽是相等的.分割后就可以求出近似多边形P的面积：S_B=$\sum\limits_{i=1}^{n}{{{S}_{{{A}_{i}}}}}$.用分割法计算出近似多边形的面积S_A与原多边形的面积S_P产生误差余项：R=S_P-S_A.

2 基于分割的近似混杂自动机

定义3  混杂自动机是一个多元组，H=(${\vec{x}}$, ϕ_init, Q, q₀, ∑, T, Act, Event).^[8]

1)${\vec{x}}$ =(x₁, …, x_n) 是变量的向量.

2)ϕ_init∈Φ((x₁, …, x_n)) 是初始条件.

3)Q是有限状态集.

4)q₀∈Q是初始状态集.

5)∑是一组事件的集合.

6) Act:Q→Φ((x₁, …, x_n, t, x₁^′, …, x_n^′)) 是活动函数Act (q) 分配到每个状态q的公式，变量t代表时间.

7)T⊂Q×Φ((x₁, …, x_n, x₁^′, …, x_n^′))×Q是一组变迁.变量x₁^′, …, x_n^′是变量x₁, …, x_n经过变迁T=T_f∪T_j后的新值：

a)T_f⊂q×Act (q)×q, q∈Q,

b)T_f⊂Q×Φ((x₁, …, x_n, 0, x₁^′, …, x_n^′))×Q.

8) Event:T→∑是变迁由事件来标记.

分析混杂自动机的基本办法是可达性分析，可达性计算是通过反复迭代计算实现的.但是，在可达性计算时只有非常小的一类，即简单多速率的混杂自动机的可达性是可判定的. ^[10]那么解决这种问题现实可行的办法就是近似，即构造一个符合设计精度要求的迭代可终止的近似混杂自动机，通过近似手段来间接研究原混杂自动机的行为.将数学中的近似技术应用到计算过程当中，得到一种有效分析的此类自动机的办法.

令X和approx (X) 分别为原值和近似值，则“近似”本身可以分为三类近似：

1)“大于”类型的近似，即

∀ X:|X|-|approx (X)|≤0，表示在任何情况下，近似后的值都大于原值；

2)“小于”类型的近似，即

∀ X:|X|-|approx (X)|≥0，表示在任何情况下，近似后的值都小于原值；

3)“交织”类型的近似，即

∀X:|X|-|approx (X)|≤∨|X|-|approx (X)|≥0，表示近似后的值在原值附近震荡变化.

为了简单起见，这里仅考虑大于和小于类型的近似机制.根据上述描述，上近似和下近似可以看作是对原系统行为从两个方面的逼近.

定义4  混杂自动机H′是混杂自动机H的 (上) 近似混杂自动机，仅当H′是通过将H的ϕ中所有函数替换为ϕ′中的相应函数得到的，并且满足[[ϕ]]⊆[[ϕ]].类似地，若替换后均有[[ϕ′]]⊆[[ϕ]]，称混杂自动机H′是混杂自动机H的 (下) 近似混杂自动机. ^[9]

在本文中运用分割法来求解近似多面体的体积，构造了一个与原系统行为非常接近的系统，根据混杂自动机的定义，推理得到一个基于分割的近似混杂自动机.

定义5  令H为混杂自动机，则混杂自动机H=(${\vec{V}}$, ϕ_init, Q, q₀, ∑, T, Act, Event由算法1经过T_R⊆Q×Φ($\left( \overrightarrow{V\left( P \right)} \right), \left( \overrightarrow{V\left( S \right)} \right)$)×Q, Event_R:T_R→∑，Act_R:Q→Φ($(\left( \overrightarrow{V\left( P \right)} \right), t, \left( \overrightarrow{V\left( S \right)} \right))$) 得到误差余项R的近似为Approx (H)=(${\vec{V}}$, ϕ_init, Q, q₀, ∑, T_R, Act_R, Event_R).

引理2   给定任意的混杂自动机H和误差余项R，根据定义5构造出的基于分割的近似混杂自动机Approx (H) 近似于H.

证明：(将算法 (Algorithm) 简写为A)

•由构造过程容易看出近似混杂自动机Approx (H) 符合混杂自动机的定义.

• ${\vec{V}}$是变量的向量；ϕ_init∈$\overrightarrow{V\left( B \right)}$是初始条件；Q是有限状态集；

•q₀=P= < F, E, V>；

•由T到T_R时，T_R={(q_1R, Φ_R, q_2R)|q_1R=A(q₁)∧q_2R=A(q₂)∧(q₁, Φ, q₂)∈T};

•由Act到Act_R时，Act_R={(q_R, Φ_R)|q_R=A(q)∧(q, Φ)∈Act};

•Event_R={(t_R, α)}, 其中 (t, α)∈Event, t∈T∧t_R∈T_R∧α∈∑, t_R=A(t).

由引理1得P⊆S，即有V(P)⊆V(S).故，给定任意的混杂自动机H和误差余项R，根据定义5构造的混杂自动机Approx (H) 近似于混杂自动机H，且属于上近似混杂自动机.

3 结语

本文定义并证明了基于分割的混杂近似自动机，从混杂系统的特征出发，用多面体表示可达集，通过分割法求解多面体体积，进而正确有效地求出混杂系统的可达集，最后证明了该方法的有效性.