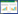文章信息
- 段耀勇, 周畅
- DUAN Yao-yong, ZHOU Chang
- 程之骥《开方用表简术》补记
- Some Notes on CHENG Zhiji's the Simple Method of Extraction with Tables(KaiFang YongBiao JianShu)
- 广西民族大学学报(自然科学版), 2017, 23(3): 18-21, 39
- Journal of Guangxi University for Nationalities(Natural Science Edition), 2017, 23(3): 18-21, 39
-
文章历史
- 收稿日期: 2017-06-03
2. 西安邮电学院 理学院, 陕西 西安 710121
2. College of Science, Xi'an University of Posts and Telecommunications, Xi'an 710121, China
在《中华大典·数学典·传统算法分典》中《开方总部》的编篡工作中,用到了文献清朝数学家程之骥的《开方用表简术》.共找到两个版本一个是来自《吴疆域图说》中的四集第六种《开方用表简术》(封面、首页和末页如图 1).此清光绪十四年(1888年)《南菁书院丛书》的刻本,但很多地方字迹不清,“筹算式”更是如此.

|
| 图 1 《吴疆域图说》中的刻本 Fig. 1 Carving copy from Description of the Territory of Wu |
经比对,另一个版本是《南菁书院丛书》的刻本的抄本(首页、末页如图 2),来自《中华大典·数学典》的电子文库,李迪先生的《算学书目汇编》有《开方用表简术》抄本记录,未看到抄本,似应与这个相同.总体而言都更清楚一些.但除原书原缺漏的地方外,又多了几处遗漏和错讹.可能是刻本不够清楚,一些“筹算式”中数字错误不少.

|
| 图 2 《南菁书院丛书》中的抄本 Fig. 2 Codex from Nanjing Academy Series |
2 《开方用表简术》的主要内容
《开方用表简术》一书共有60页,开篇明义,该书是对华蘅芳《开方古义》中开方算法的简化.《开方用表简术》的数学意义以及两本书之间的关系,另文介绍.
谨按:行素轩《开方古义》二卷解释《今古开方会要之图》,畅明厥恉且示图中各数为递开一数而设,因之化图立表为开正商递加一之用.复将表数变作正负相间为开负商递加一之用.又推增表中倍数,为开正负各商递加二之用,共成四表.证以算草佐以论说固己理,祥法备矣.惟是原术用表,必迭次递求余式,始开的元之一位商数,其在平方、立方本自便矣.倘在多乘方式而元数又有多位布算,仍觉甚繁.爰从原表推得表若干,通并原表计之遂成九个正商分表,九个负商分表,再将各表首层之数,依次垒为一个正商总表,一个负商总表,无论开何乘方,必先于总表得初商,继于分表求余式,复于总表求次商,循是以推,凡多求一次余式,即多得一位商数,拟名《开方用表简术》,盖似较原术可略从简省云[1].
随后给出“术”,即开方的操作过程,然后是附表,即九个正商分表和一个正商总表,并给出了造表通法.之后是负商表一、负商表二和负商总表.其他负商表未列出.比如,由正商总表构造正商三之表的造表法:每行保留最后一层的“1”,然后与的列“3n,9,27,81,243,729,2187,6561”,“齐其行次”对应相乘如下(原为筹式,改为阿拉伯数字).
|
最后是四个题目和详细的解题过程.包括开平方2题,开立方和开三乘方各1题目, 共计4个题目.
| $ \begin{align} &1){{x}^{2}}-5x+6=0;2)-{{x}^{2}}+56x-786=0;3)-{{x}^{3}}+2{{x}^{2}}+5x-6=0 \\ &4)-{{x}^{4}}+20230{{x}^{3}}-139638900{{x}^{2}}+3595622065905x-143010419011499=0 \\ \end{align} $ |
通过比较和计算发现,刻本尽管不少地方不清楚,但相对而言错误较少.可以两者结合在一起看,不清楚部分的问题可以解决.但是开三乘方一题漏缺部分内容,抄本漏的还要多一点.今按照其算法补校如下,并将筹码改为阿拉伯数字.正商五之表的第三行从上到下应为25,10,1.两个版本中第二个数字都误为0,应该是10中漏掉了第一个筹码.从后面开三乘方正确使用的该表看,也是如此.

|
| 图 3 “正商五之表”两个版本的抄本对比 Fig. 3 Two Versions of codex from Table of Zheng Shang Wu |
漏缺的部分主要集中在第4题开三乘方的运算中,刻本49页和50页,抄本48页和49页.从对比中可以看出,抄本漏的更多一些.

|
| 图 4 “开三乘方运算”刻本和抄本对比 Fig. 4 Carving copy versus codex of Kai San Cheng Fang Operation |
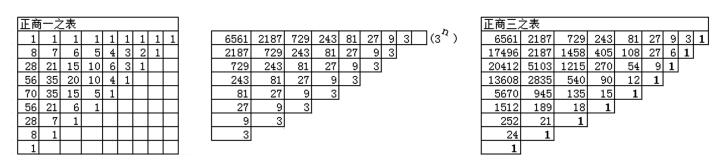
“又逐层书其并数于左:”(下面黑体数字一列原书丢失)
|
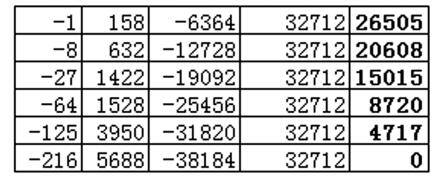
“又因末商六,乃取正商六之表前四行与上横式齐其行次,逐层相乘得数如下:”(下面计算为补校内容)

|
[并数可去首层0,一下三层作平方式,又将平方式方进一位,隅进两位横列之,与正商总表相乘得数如下:]
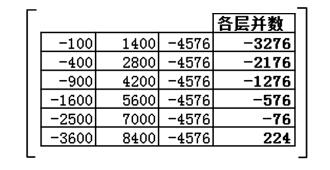
|
具体计算过程如下:

|
贾宪所创“增乘开方法”即求高次幂正根的方法,是高次方程数值解的一般方法,也称霍纳法.目前中学数学中的综合除法,其原理和程序都与它相仿.增乘开方法比传统的方法整齐简捷,又更程序化,在开高次方时,尤其显出它的优越性.增乘开方法的计算程序大致和欧洲数学家霍纳(1819年)的方法相同,但比他早770年.增乘开方是将《九章算术》开方术归纳、推广的结果,而贾宪三角是记录了用增乘法得到的各乘方之廉.增乘开方的发展脉络是:传统开方-立成释锁[2]-释锁求廉本源(贾宪三角的造表法)-增乘开方.
之后,该算法在明朝失传.清中叶之后,人们重新认识了增乘开方法,李锐和焦循对增乘开方法进行概括和总结,因为在开方方法上没有实质变化,该部分的相关内容将在方程论部分继续讨论.开方术发展到晚清受到西学东渐的影响,中算家夏鸾翔基于级数展开开方新术比戴煦的方法更为简捷有效[3].
清朝,几乎所有著名的数学家都投入了对秦九韶等开方术的研究,并在方程的分类,根的讨论以及根与系数的关系等方程论的内容得到了很多结果.清朝数学家华蘅芳创立了基于“开方诸表”的开方法,他误以为就是秦九韶的开方法,但是他的方法实不如增乘开方法简单,却也是一种创见.从程之骥的《开方用表简术》来看,确实比华蘅芳的方法简单了一些,但是整个开方过程仍然相当繁琐.而且他和华蘅芳的方法内在本质上与增乘开方法一致,也符合中算喜欢用“表”来开方的习惯,从这个意义上来说,很像增乘开方和立成释索的组合,不妨称之为“增乘立成”开方法.当然,这种方法有自己的优点,对于高次方程多个根,不论是正数根还是负数根的求解还是很顺畅的.与李锐所用传统开方法求多个根的方法“凡平方可以开两数者,以正商步负实,得第一数,小数也.以负隅步正方得第二数,大数也.立方可开三数者,以正方步负实,得第一数,小数.以负廉步正方,得第二数,中数.以正隅步负廉,得第三数,大数.它皆仿此.”[4]相比,“增乘立成”方法有其优点.
| [1] | 程之骥.开方用表简术[M].清光绪十四年(1888年)南菁书院的刻本:1-61. |
| [2] | 李迪. 对"如积释锁"的探讨[J]. 内蒙古师范大学学报:自然科学版, 2001(2): 167–172. |
| [3] | 张升, 张楠. 戴煦与夏鸾翔开方术的算法复杂度比较[J]. 内蒙古师范大学学报:自然科学版, 2012(4): 436–439. |
| [4] | 李锐. 开方说(卷上)[Z]. |
 2017, Vol. 23
2017, Vol. 23