2. 中国石油化工股份有限公司石油化工科学研究院, 北京 100083
2. SINOPEC Research Institute of Petroleum Processing, Beijing 100083, China
丙烯是仅次于乙烯的重要化工原料,目前全球对丙烯的需求快速增长,甚至超过了对乙烯需求的增长速度。作为蒸气裂解副产物的丙烯已经不能满足市场需求,因而石化/炼油行业正积极研发增产丙烯的方法。中石化开发的深度催化裂解(DCC)技术突破了常规催化裂解(FCC)的工艺限制,可成倍地增加丙烯产率[1]。提升管反应器是催化裂解工艺技术常用的一种反应器类型,是整个装置的核心反应器,具有线速高、停留时间短的特点[2]。催化裂解反应是一个快速反应过程,其特点是气体空速高、停留时间短、反应条件温和(压力 < 0.2 MPa,温度 < 600 ℃)。在DCC反应器内,催化剂和原料油的质量比(以下简称剂油比,CTO)较高(约10),停留时间约为2 s,因此该反应器内为典型的稠密气固快速反应过程[3-4]。
催化裂解反应器内化学反应复杂、反应速率快、多相湍流流动,采用数值模拟方法能获得反应器内详细的反应流动信息,但其准确性受数学模型影响很大[5-6]。由于催化裂化和催化裂解是对不同产物工艺的区分,因此,对催化裂化工艺的研究也能帮助对催化裂解工艺的研究。为了更好地研究催化裂化工艺中提升管反应器的性能,众多学者采用不同的多相流动模型和催化裂化反应模拟模型进行相关研究[7]。Theologos等[8-11]首次将三维计算流体力学(CFD)流动模型与集总动力学模型相结合,用于催化裂化反应流动数值模拟,但模型中未考虑湍流流动特性,且反应模型也是最简单的3集总动力学模型。Gao等[12-13]在其基础上,选用k-ε-kp两相湍流模型模拟催化裂化反应器内的湍流流动,耦合了13集总动力学模型模拟重油催化裂化反应,但未考虑催化剂失活对反应的影响。Wu等[14](结合Deen等[15]、van der Hoef等[16]、Zhu等[17])采用欧拉-拉格朗日方法模拟催化裂化过程气固两相流动,结合带催化剂失活动力学的4集总动力学,对提升管和下行床反应器内的催化裂化反应流动进行了研究,很好地揭示提升管和下降管中不同返混行为对反应器性能的影响。催化裂解和催化裂化均属于裂化反应,对于集总动力学来说,采用的是相同的集总,因此本研究将在前人研究的基础上,建立包括双欧拉模型、12集总反应动力学模型和催化剂的失活动力学模型的综合模型对DCC反应器内的重油催化裂解反应流动过程进行研究,分析提升管中各组分的径向和轴向的分布特性,考察剂油比、原料中沥青质含量以及提升蒸气量对管内反应流动的影响。
2 数学模型 2.1 气固流动模型假设进入提升管反应器内重油组分在高温催化剂加热作用下,迅速汽化为烃类蒸气,可将其简化为稠密气固两相流。提升管反应器内催化剂(分散相)浓度相对较高,研究采用欧拉-欧拉双流体模型刻画反应器内的气固两相流动,并采用Realizable k-ε模型对雷诺时均后的N-S方程雷诺应力相进行封闭,详细的控制方程及湍流模型[18]如表 1所示。流体相和分散相之间的阻力是提升管中的主导力之一,该参数是通过阻力定律计算的。气固相间动量交互阻力系数模型主要包括Gidaspow[19]、Syamlal and O’brien[20]和Yang[21]等,本研究选用Gidaspow模型;模型中给出了用于预测固相压力的弹性模量G以提高模型的准确度。
|
|
表 1 气固两相流的控制方程和湍流模型 Table 1 Governing equations and turbulent model for gas-solid flow |
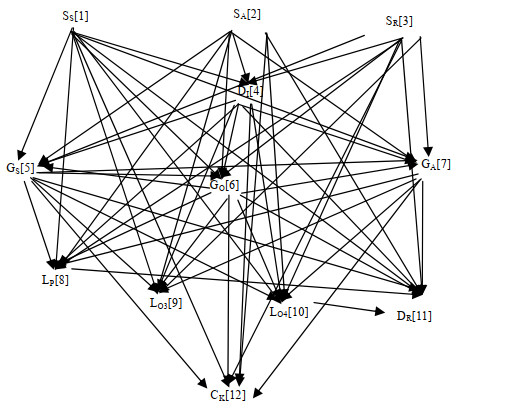
目前针对重油催化裂解的模拟方法主要有分子动力学和集总动力学方法。分子动力学计算量较大,集总动力学较为成熟,且便于与CFD模拟同时应用,本研究主要模拟催化裂解提升管内丙烯、丁烯、柴油、汽油和焦炭的生成及分布,因此选用包含以上集总构成的12集总动力学模型来描述催化裂解反应[22],其中原料和产物分别分为3集总和9集总,如表 2所示。在12集总反应网络中,使用56个反应来表示催化裂解过程,如图 1所示,图中[1]~[12]为集总1~12。反应动力学参数如表 3所示。假设反应均是一阶不可逆反应,催化剂失活是非选择性的。组分i在第r个反应中的反应速率ri, r如式(17)所示[23]:
|
|
表 2 动力学模型中的集总 Table 2 Lumps of the kinetic model |
|
|
表 3 12集总动力学模型的动力学参数 Table 3 Kinetics parameters of the 12-lump kinetic model |
| ${r_{i, r}} = - \varphi \left( C \right) \cdot F\left( N \right) \cdot F\left( A \right) \cdot {k_r} \cdot \left( {{\rho _g}{\alpha _i}} \right) \cdot {\rho _{\rm{s}}}{\varepsilon _{\rm{s}}}$ | (17) |
假设满足阿伦尼乌斯公式:
| ${k_r} = {k_0} \cdot \exp \left( { - \frac{E}{{RT}}} \right)$ | (18) |
| $\varphi \left( C \right) = {A_0}\exp ( - \alpha 'w)$ | (19) |
| $F\left( A \right) = \frac{1}{{1 + {K_A}\left( {{w_{\rm{A}}} + {w_{\rm{R}}}} \right)}}$ | (20) |
| $F\left( N \right) = \frac{1}{1 + {K_{\rm{N}}}{w_{\rm{N}}}}$ | (21) |
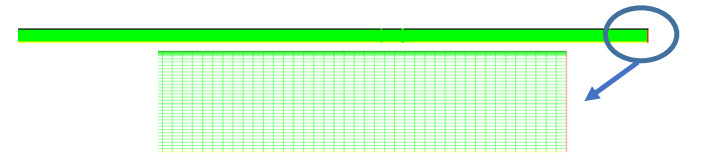
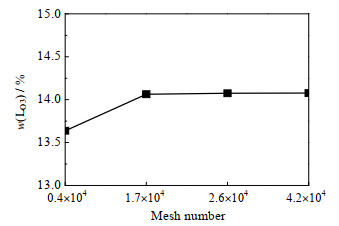
利用计算流体力学软件Fluent进行计算,其中12集总反应动力学模型通过自定义函数(UDFs)加载到模型中。提升管反应器直径为1.16 m,长度为30.2 m,由于反应器为等径直管,且高径比较大,为了减小计算量,选用2维轴对称网格对计算区域进行离散,如图 2所示。为了考察网格数量对计算结果的影响,分别考察了网格数量为0.4×104、1.7×104、2.6×104、4.2×104下的流动反应情况,并统计了出口丙烯质量分数w(Lo3)与网格数量的关系(如图 3所示),可以看出当网格数量大于1.7×104时,模拟结果基本一致,为此本研究取网格数量为2.6×104。计算参数和工况如表 4所示,组分的物理特性如表 5所示。计算中,催化剂和原料油入口选用质量流量入口边界条件,顶部物质出口选用压力出口边界条件,反应器壁面选用绝热无滑移边界条件。为了确保计算的稳定性和收敛性,计算变量的松弛因子取0.1。
|
图 2 计算网格 Fig.2 Computational grid |
|
图 3 网格无关性验证图 Fig.3 Grid independence verification graph |
|
|
表 4 计算参数 Table 4 Computation conditions |
|
|
表 5 物料的物理性质[22] Table 5 Physical properties of reactive species, catalyst and steam |
表 6给出了标准工况下(CTO=10,入口蒸气量为16 t·h-1,沥青质量分数为5.90%)有催化剂失活模型(Case1)和无催化剂失活模型(Case2)模拟得到的出口产物数据(LPG为Lo3、Lo4、Lp这三者的总和),并与工业数据进行对比。从表中可以看出Case1的模拟结果与工业数据基本吻合,主要产物的偏差均在3% 内,而Case2的模拟结果偏差较大,说明加入催化剂失活模型后构建的流动与反应模型可以更准确地描述催化裂解反应过程。对出口温度也进行了比较,工业数据中出口温度为810.0 K,Case1和Case2中出口温度分别为811.4和813.3 K,与工业数据基本吻合。
|
|
表 6 产物分布 Table 6 Product distribution |
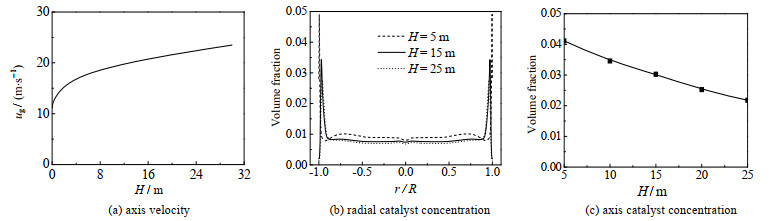
对Case1下的反应器中心轴线气体速度分布和径向催化剂浓度分布进行分析,如图 4所示。从图 4(a)中可以看出,随着催化裂解反应的进行,大分子裂解成小分子,使得气体体积增加,因此气速不断增大。在反应器前段,反应比较剧烈,气速从11 m·s-1迅速增加,之后缓慢增加到出口的24 m·s-1。
|
图 4 中心轴线气速分布和催化剂浓度分布 Fig.4 Axis gas velocity and catalyst concentration |
图 4(b)给出了催化剂颗粒在距离提升管底部的不同高度(H=5、15、25 m)处的径向浓度分布,从图中可以明显看出,催化剂颗粒在边壁处的浓度要远大于管中心的浓度,即壁面有明显的催化剂颗粒富集现象。这是因为催化剂颗粒在运动过程中与壁面发生碰撞,导致能量损失,从而降低颗粒速度,再加上边壁附近气体有明显返混现象,因此造成了催化剂颗粒在壁面附近富集。图 4(c)为催化剂颗粒边壁和中心的浓度差随高度变化,从图可知,高度越低,催化剂边壁和中心浓度差距越大。催化剂的边壁富集会导致边壁处的反应速率比管中心大。
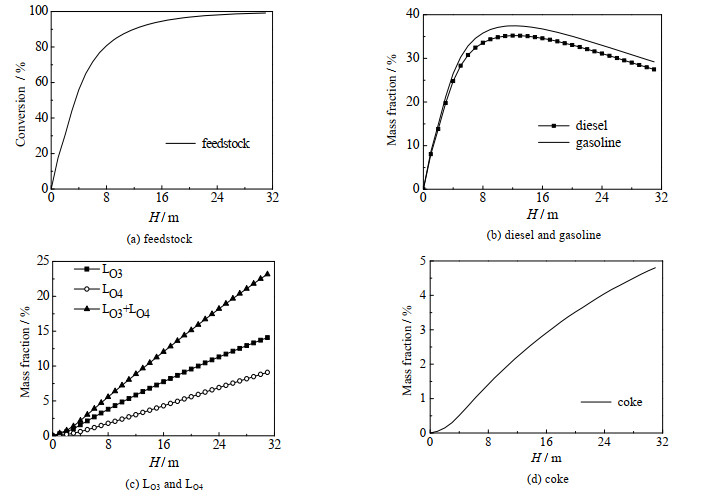
图 5分别为中心轴线上原料转化率和物料浓度分布。从图 5(a)中可以看出原料在H=8 m之前,转化率随高度基本按线性快速增大,之后,转化率随高度增加缓慢增加。在提升管中部(H=15 m)处原料转化率已达到90% 以上。从图 5(b)中可以看出,柴油和汽油的质量分数都是先迅速升高,到达最大值(35.2%和37.5%)后再缓慢下降到出口的27.5% 和29.2%,这是由于原料先迅速裂解产生汽油和柴油,之后随着裂解反应的进一步进行,柴油和汽油再裂解生成小分子。在整个反应器内,汽油的质量分数大于柴油的质量分数。从图 5(c)和图 5(d)中可以看出,丙烯、丁烯和焦炭的质量分数随着高度的升高而不断增大,到出口处分别增大到14.1% 和9.1%。
|
图 5 轴向原料转化率和组分质量分数分布 Fig.5 Axial feedstock conversion and species weight fraction |
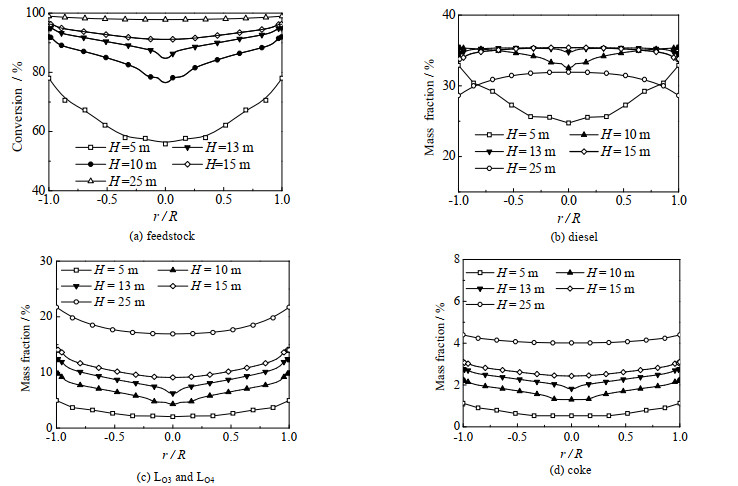
图 6是不同高度H(5、10、13、15和25 m)处的径向原料转化率和物料浓度分布图。从图 6(a)中可以看出原料转化率在径向上呈中间低两边高的趋势,即中间转化率较低,管壁处转化率较高,在提升管下段这种趋势比上段更明显。从图 6(b)可以看出,在提升管下段柴油质量分数中间处较低,管壁处较高;而在提升管上段柴油质量分布中间较高,边壁较低。这是由于在提升管下段主要为生成柴油的反应,而在提升管上段主要为裂解柴油的反应。又由于催化剂的边壁富集现象导致边壁处的反应更充分,因此提升管下段边壁处柴油生成较多,柴油质量分数较高,提升管上段边壁处柴油裂解较多,柴油质量分数较低。从图 6(c)和图 6(d)中也可以看出,由于边壁处催化剂存在附壁现象,因此焦炭、丙烯和丁烯的质量分数比中心要高。
|
图 6 径向原料转化率和组分质量分数分布 Fig.6 Radial feedstock conversion and species concentrations |
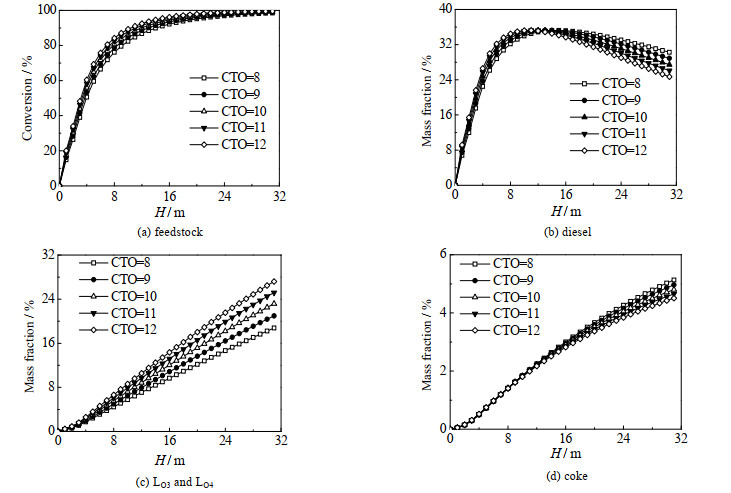
剂油比CTO是石油催化裂解工艺中一个重要的工艺参数,因此对不同剂油比(CTO=8~12)的工况进行模拟,结果如图 7所示。从图 7(a)中可以看出CTO越高,原料转化越快,出口原料质量分数越小,这是由于反应速率与催化剂量呈正比,CTO的增加促进了催化裂解反应的进行。从图 7(b)可以看出,CTO越大,反应越快,因此柴油质量分数达到最大值的H越低,而柴油质量分数的最大值不随CTO的改变而改变,始终为35.2%。CTO的增加也导致柴油裂解成小分子的反应速率增加,随着CTO从8增加到12,出口处柴油质量分数从30.3% 下降到24.7%。从图 7(c)可以看出同一高度处丙烯和丁烯的质量分数随CTO的增加而增加;随着CTO从8增加到12,出口处丙烯+丁烯的质量分数从18.8% 增加到27.2%。从图 7(d)中可以看出,前1/3段焦炭的质量分数不随CTO的改变而改变,之后同一高度处的焦炭质量分数随着CTO的增加而减少。这是由于随着催化剂的增加,导致生成丙烯、丁烯和低碳烷烃的反应速率增加,从而改变了反应的选择性,使焦炭的选择性变低,所以出口焦炭质量分数随CTO的增加而减少。
|
图 7 不同CTO下轴向原料转化率和组分质量分数分布 Fig.7 Axial feedstock conversion and species concentrations under different CTO |
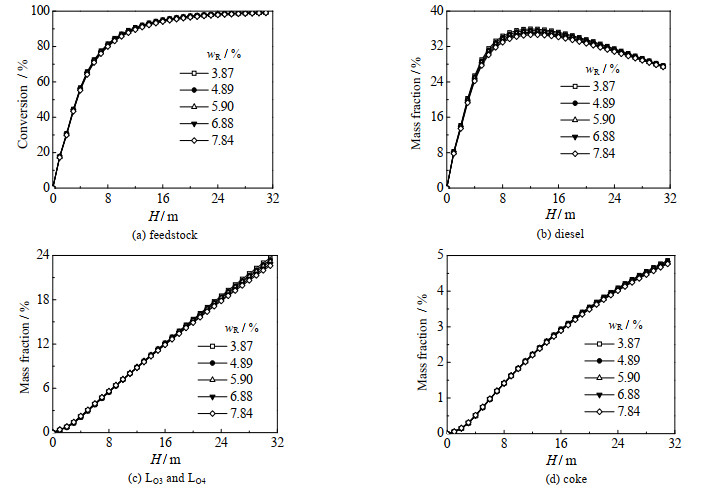
在催化裂解反应中,使用不同原料得到的产物大不相同,而沥青质质量分数wR是原料的重要参数之一。因此对不同沥青质质量分数(3.87%~7.84%)的工况进行模拟,结果如图 8和表 7所示。从图中可以明显看出,沥青质的改变相对于CTO的改变来说,对产物的影响相对较小。从表中的出口产物可以看出,随着入口沥青质质量分数提高,原料转化率随之下降,出口柴油,丙烯+丁烯和焦炭的质量分数也随着下降;随着沥青质质量分数从3.87% 增加到7.84%,出口处柴油质量分数从27.66% 减少到27.38%,丙烯+丁烯的质量分数从23.67% 减少到22.61%,焦炭的质量分数从4.86% 减少到4.76%。沥青质的提高导致由于沥青质引起的催化剂失活增加,从而减缓了反应速率。而且沥青质相较于其他物质更难发生催化裂解反应,含量增加了之后也会略微降低原料的转化率。因此对于反应来说,沥青质的质量分数越低越好。
|
图 8 不同沥青质下轴向原料转化率和组分质量分数分布 Fig.8 Axial feedstock conversion and species concentrations under different asphaltenes |
|
|
表 7 出口产物参数 Table 7 Product mass fraction |
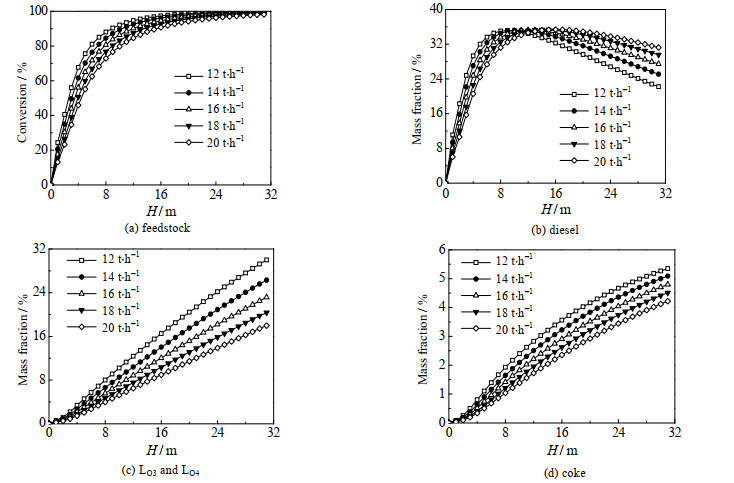
蒸气量的大小影响了反应器内表观气速和结焦的情况,因此对不同入口蒸气量(12 ~20 t·h-1)的工况进行模拟,结果如图 9所示。从图 9(a)中可以看出,随着入口蒸气量提高,原料转化降低,出口原料质量分数增大。这是因为虽然蒸气不参与反应,但是蒸气量的提高增加了气速,从而导致停留时间变短。从图 9(b)可以看出,随着入口蒸气量的提高,柴油质量分数达到最高点的高度也不断增加,但是柴油质量分数的最高值不随蒸气量的改变而改变,始终为35.2%。蒸气量越大,停留时间越短,柴油的转化率也越小,因此随着蒸气量从12增大到20 t·h-1,出口柴油的质量分数也从22.2% 提高到31.2%。从图 9(c)和图 9(d)可以看出,相同高度处的丙烯、丁烯和焦炭的质量分数随蒸气量的提高而降低。
|
图 9 不同蒸气量下轴向原料转化率和组分质量分数分布 Fig.9 Axial feedstock conversion and species concentrations under different steam amounts |
本研究基于Fluent软件,建立了包括双欧拉模型、12集总反应动力学模型和催化剂的失活动力学模型的综合模型对工业DCC反应器内的重油催化裂解反应流动过程数值模拟研究,分析了反应器内的物料分布特性,研究了主要操作参数对管内反应流动的影响,得出如下结论:
(1) 模拟得到的反应器出口各组分质量分数与工业数据基本一致,说明了构建的模型具有良好的准确性。
(2) 提升管径向边壁处有催化剂富集现象,因此边壁处的反应比中心处更加充分,产物质量分数呈现中间低、两边高的趋势。
(3) CTO越大,出口丙烯和丁烯质量分数越高,柴油和焦炭的质量分数越低。原料中沥青质含量对产物的影响较小;沥青质含量越高,出口焦炭、柴油、丙烯和丁烯的质量分数越低。入口蒸气量越高,出口焦炭、丙烯和丁烯的质量分数越低,出口柴油质量分数越高。
符号说明:
|
|
| [1] |
谢朝钢. 催化裂解过程丙烯选择性的影响因数探究[J]. 石油学报(石油加工), 2018, 34(1): 1-6. XIE C G. Study on the influence factor of propylene selectivity in catalytic cracking process[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2018, 34(1): 1-6. DOI:10.3969/j.issn.1001-8719.2018.01.001 |
| [2] |
GAO H, WANG G, LI R, et al. Study on the catalytic cracking of heavy oil by proper cut for higher conversion and desirable products[J]. Energy & Fuels, 2012, 26(3): 1880-1891. |
| [3] |
罗勇, 高永灿. DCC装置降低汽油烯烃含量技术的工业应用[J]. 石油炼制与化工, 2005, 36(11): 25-29. LUO Y, GAO Y C. Industrial application of technology for reducing gasoline olefin content in DCC unit[J]. China Petroleum Processing Petrochemical Technology, 2005, 36(11): 25-29. DOI:10.3969/j.issn.1005-2399.2005.11.006 |
| [4] |
路军晓. 关于常压渣油催化裂解多产丙烯乙烯(MPE)工艺的探讨[J]. 化工管理, 2017(12): 101-101. LU J X. Discussion on the catalytic cracking of atmospheric residue to produce more propylene and ethylene (MPE)[J]. Chemical Enterprise Management, 2017(12): 101-101. DOI:10.3969/j.issn.1008-4800.2017.12.087 |
| [5] |
欧阳福生, 凌巧, 虞正恺. 灵活多效催化裂化工艺反应动力学模型研究[J]. 高校化学工程学报, 2015, 29(5): 1106-1113. OUYANG F S, LIN Q, YU Z K. Reaction kinetic model for flexible dual-riser fluid catalytic cracking process[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(5): 1106-1113. DOI:10.3969/j.issn.1003-9015.2015.00.025 |
| [6] |
CHEN Z Y, FENG S, ZHANG L Z, et al. Molecular-level kinetic modelling of fluid catalytic cracking slurry oil hydrotreating[J]. Chemical Engineering Science, 2019, 195: 619-630. DOI:10.1016/j.ces.2018.10.007 |
| [7] |
王维, 洪坤, 鲁波娜, 等. 流态化模拟: 基于介尺度结构的多尺度CFD[J]. 化工学报, 2013, 64(1): 95-106. WANG W, HONG K, LU B N, et al. Fluidized bed simulation: Structure-dependent multiscale CFD[J]. CIESC Journal, 2013, 64(1): 95-106. |
| [8] |
Theologos K N, Markatos N C. Advanced modeling of fluid catalytic cracking riser-type reactors[J]. AIChE Journal, 1993, 39(6): 1007-1017. DOI:10.1002/aic.690390610 |
| [9] |
THEOLOGOS K N, MAROULIS Z B, MARKATOS N C. Simulation of transport dynamics in fluidized-bed dryers[J]. Drying Technology, 1997, 15(5): 1269-1291. DOI:10.1080/07373939708917295 |
| [10] |
THEOLOGOS K N, LYGEROS A I, MARKATOS N C. Feedstock atomization effects on FCC riser reactors selectivity[J]. Chemical Engineering Science, 1999, 54(22): 5617-5625. DOI:10.1016/S0009-2509(99)00294-8 |
| [11] |
THEOLOGOS K N, NIKOU I D, LYGEROS A I, et al. Simulation and design of fluid-catalytic cracking riser-type reactors[J]. AIChE Journal, 1997, 43(2): 486-494. DOI:10.1002/aic.690430221 |
| [12] |
GAO J, XU C, LIN S, et al. Advanced model for turbulent gas-solid flow and reaction in FCC riser reactors[J]. AIChE Journal, 2010, 45(5): 1095-1113. |
| [13] |
GAO J, XU C, LIN S, et al. Simulations of gas-liquid-solid 3-phase flow and reaction in FCC riser reactors[J]. AIChE Journal, 2001, 47(3): 677-692. DOI:10.1002/aic.690470315 |
| [14] |
WU C, CHENG Y, JIN Y. Understanding riser and downer based fluid catalytic cracking processes by a comprehensive two dimensional reactor model[J]. Industrial & Engineering Chemistry Research, 2009, 48(1): 12-26. |
| [15] |
DEEN N G, ANNALANG M V S, HOEF M A V D, et al. Review of discrete particle modeling of fluidized beds[J]. Chemical Engineering Science, 2007, 62(1/2): 28-44. |
| [16] |
VAN DER HOEF M A, VAN SINT ANNALAND M, DEEN N G, et al. Numerical simulation of dense gas-solid fluidized beds: A multiscale modeling strategy[J]. Annual Review of Fluid Mechanics, 2008, 40(1): 47-70. DOI:10.1146/annurev.fluid.40.111406.102130 |
| [17] |
ZHU H P, ZHOU Z Y, YU A B. Discrete particle simulation of particulate systems: A review of major applications and findings[J]. Chemical Engineering Science, 2008, 63(23): 5728-5770. |
| [18] |
SPALART P R. A one-equation turbulence model for aerodynamic flows: 30th Aerospace Sciences Meeting and Exhibit[C]. Reno: [s. n. ], 1992.
|
| [19] |
GIDASPOW D. Multiphase flow and fluidization: Continuum and kinetic theory descriptions[M]. San Diego: Academic Press, 1994.
|
| [20] |
SYAMLAL M, O'BRIEN T J. Computer simulation of bubbles in fluidized bed[J]. AIChE Symposium Series, 1989, 85(1): 22-31. |
| [21] |
YANG N, WANG W, GE W, et al. CFD simulation of concurrent-up gas-solid flow in circulating fluidized beds with structure-dependent drag coefficient[J]. Chemical Engineering Journal, 2003, 96(1/2/3): 71-80. |
| [22] |
PELISSARI D C, ALVARES-CASTRO H C, VERGEL J L G, et al. Numerical investigation of influence of treatment of the coke component on hydrodynamic and catalytic cracking reactions in an industrial riser[J]. Advanced Powder Technology, 2018, 29(10): 2568-2581. DOI:10.1016/j.apt.2018.07.012 |
| [23] |
吴飞跃, 翁惠新. FDFCC集总反应动力学组合模型的建立[J]. 华东理工大学学报(自然科学版), 2009, 35(3): 350-356. WU F Y, WEN H X. Establishment of FDFCC Lumped reaction kinetics combined model[J]. Journal of East China University of Science and Technology, 2009, 35(3): 350-356. |