2. 浙江大学衢州研究院, 浙江 衢州 324000
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China
梳型聚合物是一类由线性侧链接枝到线性主链上形成的支化聚合物[1-3],在介电弹性体、药物载体、弹性体增韧材料、润滑剂、刺激响应材料、聚合物纺丝和发泡材料等领域有着广泛的应用[4-6],受到了学术界和工业界的广泛关注[7]。与线性聚合物相比,梳型聚合物因独特的链结构产生的特殊缠结行为,具有更优异的力学性能,如更低的平台模量[8-9]、更高的断裂伸长率和拉伸强度[5]等;其熔体也具有特殊的流动和形变特征,如更显著的剪切稀化现象和更高的应变硬化指数[10-12]等,使其具备更优异的加工和发泡性能。因此,探明梳型聚合物流变性能与其链结构之间的构效关系,对其设计、加工和应用具有重要的指导意义。
随着“活性”/可控自由基聚合(CRP)[13-24]、活性配位聚合[2, 25]、开环易位聚合(ROMP)[19, 26-30]等可控聚合技术的发展,可实现不同链结构参数(如主、侧链长度、支链数等)的梳型聚合物的制备[4, 7, 31-33],例如,作者所在课题组合成的梳型丙烯酸酯压敏胶[34-35]、梳型聚烯烃热塑性弹性体(CPOE) [25]、超支化聚乙烯[36-37]等。以这些聚合物为模型体系,为系统地揭示梳型聚合物流变性能与其链结构之间的构效关系提供了基础[38]。
综述通过梳型聚合物的流变特性,揭示主、侧链长度和支链数等链结构参数对其熔体的零切黏度、动态模量主曲线和平台模量等流变性能的影响,同时介绍一种用于梳型聚合物链拓扑结构的表征方法——傅里叶变换流变分析方法,以期为梳型聚合物链结构的流变分析和表征提供理论支持,并为其设计、加工和实际应用提供指导。
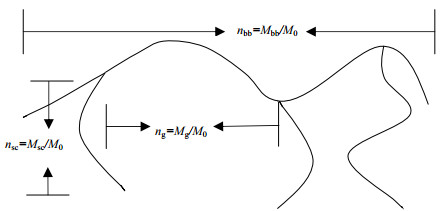
2 梳型聚合物分子链结构参数与构象定义 2.1 梳型聚合物分子链结构参数梳型聚合物的黏弹性主要依赖其高分子量链之间的缠结作用,受到主、侧链长度的影响[38]。可通过以下3个独立参数来量化其分子链结构:主链分子量Mbb、侧链分子量Msc和支链数q,它们的定义以及与其他参数间的关系分别参见图 1和表 1。图 1中的M0为一个聚合单元的摩尔质量,g·mol−1;Mg为相邻支化点之间所有聚合单元的摩尔质量,g·mol−1;nbb、nsc、ng分别为主链、侧链、支化点间的聚合度。表 1中的Me为链缠结摩尔质量,g·mol−1,是聚合物产生链缠结所需的最低摩尔质量;Zbb、Zsc、Zg分别为主链、侧链、支化点间的链缠结数目;ϕbb为主链体积分数;ϕsc为侧链体积分数。
|
图 1 梳型聚合物链结构示意图 Fig.1 Schematic diagram of chain structure of a comb-shaped polymer |
不同聚合物的Me不同,聚乙烯的Me约为1 250 g·mol−1 [39]。Me的计算式如下:
| $ {M_{\text{e}}}{\text{ = }}\rho RT/G_{\text{N}}^{\text{0}} $ | (1) |
式中:
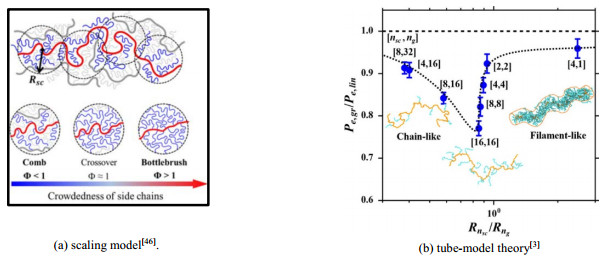
根据粗粒度分子模拟结果[3, 42-47],梳型聚合物可分为梳状(comb)和瓶刷(bottlebrush) 2类构象。根据缩比模型(scaling model),如图 2(a)所示,Liang等[14, 42, 46-47]将聚合物链等效为无数个半径为Rsc的小球(blobs),建立了如下拥挤因子Φ的表达式:
|
图 2 描述梳型聚合物的模型及其分子链构象[3, 46] Fig.2 Model and molecular chain conformation describing comb-shaped polymers[3, 46] |
| $ {{\varPhi = }}{V_\text{m}}/V $ | (2) |
式中:Vm为整条聚合物链所有聚合单元的体积之和,nm3;V为整条聚合物链的排除体积,nm3。Φ可用来描述相邻分子间的重叠程度,Φ < 1为梳状构象,Φ > 1为瓶刷构象。在瓶刷构象中,根据侧链的长短又可将构象细分为3个亚类[42]:伸展型主链(SBB)、伸展型侧链(SSC)和棒状型侧链(RSC)。前两类拥有较长的柔性侧链,最后一类拥有短的棒状侧链。
此外,根据管模型理论(tube-model theory) [48],可将聚合物视为在约束管中爬行的探针,可用一个新的、描述管尺寸的参数Pe来表示约束管中产生链缠结的聚合物链的数量[3]。研究表明,Pe, gr/Pe, lin是
| $ {{{P_{{\text{e, gr}}}}} \mathord{\left/ {\vphantom {{{P_{{\text{e, gr}}}}} {{P_{\text{e}}}_{{\text{, lin}}}}}} \right. } {{P_{\text{e}}}_{{\text{, lin}}}}}{\text{ = }}f\left( {{{{R_{{n_{{\text{sc}}}}}}} \mathord{\left/ {\vphantom {{{R_{{n_{{\text{sc}}}}}}} {{R_{{n_{\text{g}}}}}}}} \right. } {{R_{{n_{\text{g}}}}}}}} \right) $ | (3) |
式中:Pe, gr与Pe, lin分别为梳型链和线性链的管尺寸参数;
为进一步量化梳型聚合物的链构象,借助粗粒度分子动力学模拟,并结合ng、Abbasi等[12]、Paturej等[43]、Daniel等[44]将梳型聚合物的链构象分为4个区域,如图 2(c)所示,图中,ng*表示梳型聚合物从DC构象变为LB构象时,相邻侧链之间的聚合度;ng**表示梳型聚合物从LB构象变为DB构象时,相邻侧链之间的聚合度。当ng < nsc时,为松散梳状(loosely grafted comb, LC),主链与侧链均为高斯链构象;当nsc < ng < ng*时,为密集梳状(densely grafted comb, DC),主链与侧链均为高斯链构象;当ng* < ng < ng**时,为松散瓶刷(loosely grafted bottlebrush, LB),侧链为高斯链构象、主链为伸展构象;当ng > ng**时,为密集瓶刷(densely grafted bottlebrush, DB),侧链、主链均为伸展构象[43] (其中ng*表示梳型聚合物从DC构象变为LB构象时,相邻侧链之间的聚合度;ng**表示梳型聚合物从LB构象变为DB构象时,相邻侧链之间的聚合度;ng = nsc,ng* = Snsc1/2,ng** = s,S = v/(bl)3/2,s = v/(bl2);v为单体体积,l为单体长度,b为线性聚合物的Kuhn链段长度。梳状构象的侧链很容易在空间上相互穿插,发生链缠结;而瓶刷构象的侧链由于空间位阻效应,使得侧链之间相互排斥,从而减弱侧链间的链缠结。
3 梳型聚合物流变分析与表征在梳型聚合物构象理论研究基础上,人们也开展了大量流变实验,以便研究和掌握其构象变化与流变性能之间的相互关系[12, 38]。综述将重点介绍利用零切黏度、动态模量主曲线、平台模量和损耗角对复数模量图(vGP图)来定性或定量分析梳型聚合物链结构,论述Mbb、Msc和q的变化对其流变性能的影响,还将介绍一种流变分析方法——傅里叶变换流变分析方法。
3.1 零切黏度高分子聚合物熔体的零切黏度η0可用来定量描述聚合物链结构特征[49-51]。当线性高分子重均分子量Mw大于临界缠结摩尔质量Mc (Mc约是Me的2~3倍)时[39-41, 52-54],存在以下关系式:
| $ {\eta ^0} \propto M_{\text{w}}^{3.4 \sim 3.6} $ | (4) |
但梳型聚合物熔体的η0不再符合式(4)的关系,它受到Mbb、Msc和q等因素的影响。根据管模型理论[55]和蠕动模型(reptation model) [56],可量化梳型高分子的黏弹性[51, 57]。对于具有缠结侧链的高分子,侧链延缓了支化点间主链链段的旋转,从而增加了与主链之间的摩擦,其末端具有更高的移动性,比其他部分链段松弛更快;进一步增加支链数,会稀释主链的爬行管径,使主链更加伸展。因此,与线性聚合物相比,梳型聚合物的弛豫过程更复杂。
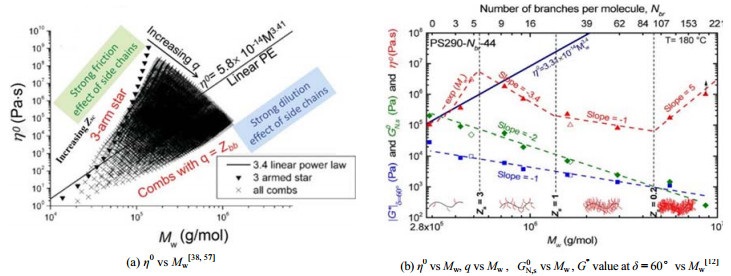
Inkson等[57]给出了具有缠结侧链和缠结主链的梳型聚乙烯(PE-g-PE)的η0计算式:
| $ {\eta ^0} \propto {\tau _{\text{e}}}G_{\text{N}}^0Z_{{\text{bb}}}^3\phi _{{\text{bb}}}^2\left( {1 - {\phi _{{\text{bb}}}}} \right)Z_{{\text{sc}}}^{1/2}\exp \left[ {\frac{{5{Z_{{\text{sc}}}}\left( {1 + 2{\phi _{{\text{bb}}}}} \right)}}{8}} \right] $ | (5) |
式中:τe为链缠结达到一个Me所需要的松弛时间,s;ϕbb≠1,6 ≤ q≤ Zbb,2 ≤ Zsc ≤ 10,10 ≤ Zbb ≤ 100,Zg ≥1。式(5)的右边可分为3部分:(1)线性链的零切黏度项(
|
图 3 PE-g-PE和PS-g-PS的零切黏度、平台模量与重均分子量之间的关系[12, 38, 57] Fig.3 Relationship between zero shear viscosity, plateau modulus and molecular weight of PE-g-PE and PS-g-PS [12, 38, 57] |
上述研究表明,链缠结、链摩擦与主、侧链分子量(即主、侧链长度)密切相关,而接枝密度不仅影响侧链的稀释效应,还会影响主链的构象[2, 12, 49, 58-64]。
主链长短影响链缠结,长主链可产生链缠结,而短主链则不会。López-Barrón等[60, 65]合成侧链长度为4~16个碳的聚α-烯烃瓶刷分子,每两个碳之间有一条短侧链,侧链远未达到缠结程度;当主链足够长时(Mbb=1 650~6 290 kg·mol−1、Zbb=53~451),聚合物熔体呈现出与线性链一样的缠结现象[65],聚烯烃瓶刷链可视为半径增厚的高斯链;当主链很短时(Mbb=33~50 kg·mol−1、Zbb=0.30~1.45),则不发生链缠结[60],聚合物熔体的流变行为可与Rouse模型吻合良好[66]。
侧链长短影响链摩擦和链缠结。Dalsin等[58]合成了带有降冰片烯(NB)官能团的无规聚丙烯大单体(aPP)和乙烯/丙烯大单体(PEP),通过ROMP方法分别合成PNB-g-aPP (nbb=11~732、Msc=2.05 kg·mol−1、Zsc≈0.5)和PNB-g-PEP (nbb=13~627、Msc= 6.7 kg·mol−1、Zsc≈3.5),每5个碳有一条侧链。研究发现,长侧链的PNB-g-PEP熔体拥有更高的η0:在主链长度相同的情况下,长侧链的η0比短侧链的高了近十倍,这表明侧链链缠结的存在极大地增加了链摩擦。ZHANG等[25, 67]合成了主链为乙烯/1-辛烯的无规共聚物(POE)、侧链为PE的CPOE (Mbb=80~100 kg·mol−1、Msc=5~25.8 kg·mol−1、q=0~5),简称POE-g-PE,发现最长侧链的η0比最短侧链的高6倍,力学性能与陶氏EngageTM 8150相当。
支链数q即接枝密度影响链构象。随着接枝密度的提高,主链由高斯链逐渐变为伸展链,构象也由梳状变为瓶刷,松弛机制由爬行松弛(蠕动松弛)变为Rouse松弛[12, 58-59, 61-64, 68-69]。Abbasi等[12]通过阴离子聚合技术合成了主、侧链均为聚苯乙烯(PS)的梳型聚合物(PS-g-PS,Zbb=20、Zsc=3、q=0~190),在实验所得的数据范围内,PS-g-PS的η0呈现先升高后降低再升高的趋势,见图 3(b),图中G*为损耗角δ=60°时的复数模量,Pa;
对于接枝密度更高的DB构象,η0与Mw之间的关系类似不缠结的线性Rouse链。随着主链聚合度的增加,整个瓶刷分子从球形或纺锤形构象,逐渐转变成棒状或圆柱状构象[63-64],直至变为半柔性高斯链[62]。由于DB构象中主链和侧链均完全伸展,所以,无论主链和侧链长与短,其η0与Mw之间均呈现正比例关系[58, 62-64, 69]。
Dalsin等[58, 62-63, 70]通过ROMP方法,以降冰片烯二甲酯(DME)为稀释剂,合成了主链为NB、侧链为聚乳酸(PLA)的梳型聚合物(PNB-g-PLA,nbb=40~1 800、Msc=3.5 kg·mol−1、Zsc≈0.4、ng=2.7~53.6),研究了PNB-g-PLA的约化零切黏度(η0/αT)对Mw的标度关系(αT为平移因子),发现其η0/αT存在2个标度区域,如图 4(a)所示,幂指数分别为1和3,这2个区域中链松弛分别与Rouse松弛和爬行松弛有关。如图 4(b)所示,图中Tg为玻璃化转变温度,将Mw无量纲为Mw/Me,并以此为x轴。由图可见,当Mw/Me=1时,Rouse松弛和爬行松弛存在一个转折点,这说明梳型聚合物本质上与线性聚合物类似。当聚合物由梳状构象转变为瓶刷构象时,其η0/αT对Mw的幂指数从3变为1,松弛机制也由爬行松弛变为Rouse松弛[38, 68]。
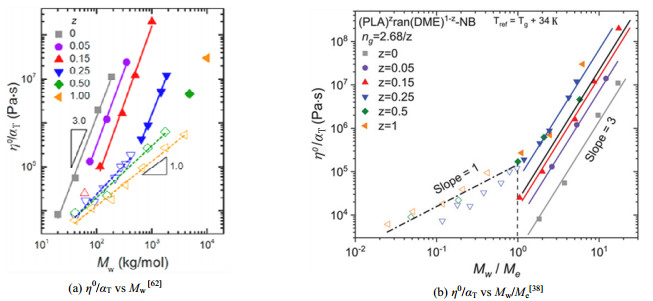
|
图 4 PNB-g-PLA的约化零切黏度与重均分子量关系图[38, 62] Fig.4 Reduced zero-shear viscosity versus weight-average molecular weight of PNB-g-PLA [38, 62] |
利用动态模量主曲线可研究聚合物熔体的完整松弛过程,通过如下WLF方程[71],平移得到动态模量主曲线:
| $ \log {\alpha _\text{T}}{\text{ = }}\frac{{ - {C_{\text{1}}}\left( {T - {T_{{\text{ref}}}}} \right)}}{{{C_{\text{2}}} + \left( {T - {T_{{\text{ref}}}}} \right)}} $ | (6) |
式中:Tref为参比温度,K;C1、C2为常数。
具有简单热流变行为的聚合物熔体满足时温等效原理(TTS),即低温下长时间的松弛过程,等同于高温下短时间发生的松弛;而具有复杂热流变行为的聚合物,因其多存在微相分离,很难通过平移得到动态模量主曲线。为避免梳型聚合物出现微相分离,通常使其主链体积分数小于1%[27, 58, 62, 69, 72],或者使主链与侧链的化学性质相近[12, 14, 60, 64]。
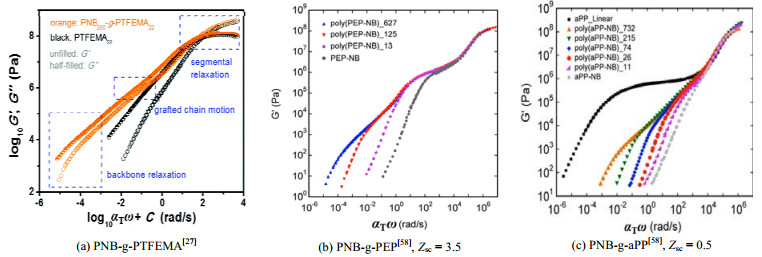
Xu等[27]合成了NB修饰的聚甲基丙烯酸三氟乙酯大单体(PTFEMA),通过ROMP方法合成了主链为NB、侧链为PTFEMA的梳型聚合物(PNB-g-PTFEMA,nbb=21~200,Msc=13.8 kg·mol−1),每5个碳有一条侧链。发现其熔体具有简单热流变行为,如图 5(a)所示,在动态模量主曲线中按链段(segment)、侧链(side chain)和主链(backbone chain)分层级松弛(hierarchy relaxtion) [27, 60, 73]。图中,ω为频率,r·s−1;ωαT为校正频率,r·s−1;G′为储能模量,Pa;G″为损耗模量, Pa。动态模量主曲线可分为3个部分:高频链段松弛区域,反映玻璃态模量大小,松弛机制只与单体种类有关,与链拓扑结构无关[58];中频侧链松弛区域,长侧链在此区域有明显的侧链模量平台(见图 5(b)),而短侧链没有(见图 5(c));低频主链松弛区域,随着主链链长增加,该区域会出现主链模量平台,曲线末端会向低频移动,松弛所需时间延长。
在侧链和主链松弛区域之间,还存在一个过渡区域[64],该区域受接枝密度的影响[62],可反映主链构象的变化。Dobrynin研究团队[14]通过原子转移自由基聚合(ATRP)合成主、侧链均为聚丙烯酸正丁酯(PBA)的梳型聚丙烯酸正丁酯(PBA-g-PBA,nbb = 2 000~3 000、nsc = 13~15、ng = 68~6),实验发现随着ng减小,聚合物构象从梳状变为瓶刷,其黏弹性逐渐向黏性转变。在ng = 6时(见图 6),整个频率范围内G″恒大于G′。在过渡区域出现G′≈G″现象,这种现象与侧链对主链的屏蔽效应有关[58]。对于高接枝密度的DB聚合物,在过渡区域,G′与G″互相平行,接近相等,且是频率ω的幂函数,幂指数约为0.6 [12, 14, 27, 58, 60, 62, 64, 69, 74-76]:
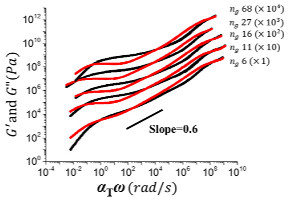
|
图 6 不同ng的PBA-g-PBA的动态模量与校正频率之间的关系[14] Fig.6 Relationship between dynamic modulus and correction frequency of PBA-g-PBA with different ng [14] (nbb=2 000~3 000, nsc=13~15, ng = 6 ~68, Tref= 343 K) |
| $ G'\left( \omega \right) \cong G''\left( \omega \right) \propto {\omega ^{0.6}} $ | (7) |
Wang等[34-35]通过开环反应合成了丙交酯(LLA)与己内酯(CL)的无规聚酯大单体(PLC),并将PLC、丙烯酸(AA)与丙烯酸异辛酯(EHA)共聚,制得梳型丙烯酸酯共聚物(PAE-g-PLC,Mbb=92~205 kg·mol−1、Msc=2.04~7.68 kg·mol−1、q=8~29)。研究发现,在过渡区域,G′与G″互相平行,且是ω的幂函数,幂指数约为0.5,呈现Rouse松弛的流变特征。
上述关系也可用如下线性聚合物的Rouse模型[66]和Zimm模型[77]来解释:
| $ \text{Rouse:}\quad\quad\quad\quad\quad\quad\quad\quad\quad G'\left( \omega \right) \cong G''\left( \omega \right) \propto {\omega ^{1/2}} $ | (8) |
| $ \text{Zimm:}\quad\quad\quad\quad\quad\quad\quad\quad\quad G'\left( \omega \right) \cong G''\left( \omega \right) \propto {\omega ^{2/3}} $ | (9) |
这2种模型最初都是用于聚合物稀溶液体系,Zimm模型比Rouse模型预测的松弛过程更快,可更好地描述实际聚合物溶液。Zimm模型通过合并水力学相互作用来校正Rouse模型的标度关系,由于流体线团中链段的运动受周围流场干扰,聚合物内部链段被排除体积中的溶剂包裹形成球形结构,使溶剂不能穿过排除体积,因此聚合物链段对整个流场的黏性阻力没有贡献[77];而Rouse模型则忽略了流体水力学的相互作用,采用了平均场的方法,即所有聚合物链段对总黏度的贡献相等[66]。因此,Rouse模型能更好地描述不缠结线性链熔体的流变行为。对于高接枝密度的瓶刷聚合物熔体,由于微观尺度上梳型高分子侧链的密集堆叠,内部链段不接触周围分子,侧链相当于溶剂,起到了屏蔽主链的作用,但由于侧链并不是真正的溶剂,因此,瓶刷分子可被当作粗的高斯柔性链,其松弛行为有望被Rouse模型进行描述[58]。
3.3 平台模量在梳型聚合物中,随着接枝密度的提高,主链体积分数ϕbb会被侧链所稀释,可使主链所在的爬行管径变大,其平台模量
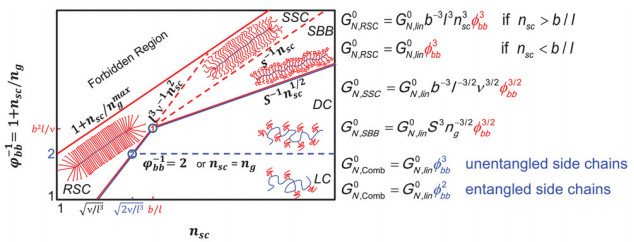
|
图 7 梳型聚合物链构象和平台模量的理论计算[38] Fig.7 Comb-shaped polymer chain conformation and theoretical calculation formula of plateau modulus[38] |
为验证计算结果的准确性,Lewis等[80]分析获得了2个基于聚α-烯烃平台模量的经验方程:
| $ G_{\text{N}}^{\text{0}}{\text{ = 24}}\, {\text{820}}m_{\text{b}}^{ - 3.49}\quad \quad \quad \quad \left( {{m_{\text{b}}}{\text{ = }}14 \sim 28{\text{ g}} \cdot {\text{mo}}{{\text{l}}^{ - 1}}} \right) $ | (10) |
| $ G_{\text{N}}^{\text{0}} = {\text{41}}{\text{.84}}m_{\text{b}}^{ - {\text{1}}{\text{.58}}}\quad \quad \quad \quad \left( {{m_{\text{b}}}{\text{ = }}35 \sim 56{\text{ g}} \cdot {\text{mo}}{{\text{l}}^{ - {\text{1}}}}} \right) $ | (11) |
式中:
| $ G_{\text{N}}^{\text{0}} = {\text{1}}{\text{.05}}n_{{\text{sc}}}^{ - {\text{1}}{\text{.47}}} = 1.05{\left( {\frac{1}{7}{m_{\text{b}}} - 2} \right)^{ - 1.47}} \quad \quad \quad \left( {{m_{\text{b}}}{\text{ = }}42 \sim 126{\text{ g}} \cdot {\text{mo}}{{\text{l}}^{ - {\text{1}}}}} \right) $ | (12) |
将式(12)变换后可得到
需要指出的是,图 7中SBB、SSC和RSC这3种类型的瓶刷聚合物的标度分析仅针对未达到缠结摩尔质量Me的短侧链,对于达到Me的长侧链瓶刷聚合物,是否能满足图 7中的理论模拟还需进一步研究[58]。
3.4 vGP图vGP图用于表征聚合物的多分散性[81-82]和分子量[83],之后拓展到表征聚合物链拓扑结构[2, 84-85],用于定性分析聚乙烯/α-烯烃共聚物中共单体[86]和长侧链含量[82]的影响。具有热流变简单行为的聚合物熔体在不同温度下的vGP曲线能直接叠加在一起,无需平移处理;而存在相分离的具有热流变复杂行为的聚合物,不经过曲线平移无法叠加在一起,所以vGP图可用于验证时温等效原理的有效性,以判断聚合物是否发生了相分离[58]。
对于线性聚合物,随着复数模量G*的减小,损耗角δ会先达到一个最小值(δmin),再升高到极限值90°,反映了聚合物链的松弛过程,δmin处代表高分子链的黏弹性转变。随着分子量增加,δmin处所对应的复数模量值
梳型聚合物既有低分子量的侧链又有高分子量主链,因此其vGP图中存在两个松弛过程,与二元共混聚合物相似[2, 12, 58, 61, 64, 69, 83, 88]。对于PS-g-PS (Zbb=20、Zsc=3、q=0~190),如图 8所示,δmin处是聚合物熔体黏弹性的转变点,
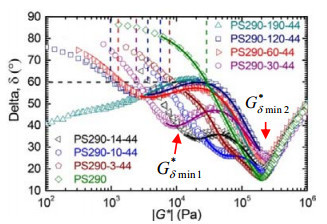
|
图 8 不同接枝密度的PS-g-PS的vGP图[12] Fig.8 vGP diagrams of PS-g-PS with different grafting densities [12] (Mbb=290 kg·mol−1, Zbb=20, Mw=4.4 kg·mol−1, Zsc=3, 0 < q≤190, Tref = 453 K) |
傅里叶变换流变通过对剪切震荡应力正弦波的傅里叶变换[93],可用于中等剪切震荡(MAOS)和大振幅剪切震荡(LAOS)条件下的聚合物黏弹性研究,而小振幅下的聚合物剪切震荡(SAOS)位于线型区。在固定频率下,通过流变仪的转子在聚合物膜片上施加固定振幅的应变,再由传感器检测转子所受应力大小,得到应力正弦波,见图 9(a)。随着振幅增大,聚合物熔体从线型区过渡到非线性区,检测到的应力不再是标准的正弦波,而不同拓扑结构聚合物对应着不同的波形[94]。通过傅里叶变换,可将应力变化曲线转换为如式(13)所示的一系列叠加的三角函数,从而得到其在非线性区的拟合函数[93-95]。
| $ \sigma \left( t \right){\text{ = }}\sum\limits_{n, {\text{odd}}}^\infty {{I_n}\cos \left( {n\omega t + {\varphi _n}} \right)} $ | (13) |
式中:σ(t)为转子所施加的剪切应力,Pa;In为n阶谐波强度,Pa;t为时间,s;n为傅里叶变换阶数;φn为相位角。
经傅里叶变换可得到奇数谐波强度(见图 9(a))和第三阶谐波相对强度I3/1,表达式如下:
| $ {I_{3/1}}\left( {\omega , {\gamma _0}} \right) \equiv \frac{{{I_3}}}{{{I_1}}} $ | (14) |
式中:γ0为应变,%。将I3/1对γ0作图,如图 9(b)所示。由图可见,低γ0下I3/1未呈现明显规律,这是由于在小应变下,材料本身的非线性不强;随γ0增大,I3/1∝
Hyun等[104]定义了非线性系数Q(ω, γ0)如下:
| $ Q\left( {\omega , {\gamma _0}} \right) \equiv \frac{{{I_{3/1}}\left( {\omega , {\gamma _0}} \right)}}{{\gamma _0^2}} $ | (15) |
由图 9(c)可见,Q(ω, γ0)在MAOS区域内为常数,而在LAOS区域内,Q(ω, γ0)随γ0增大而减小。类比于零切黏度的定义,在MAOS区域内可将Q(ω, γ0)向γ0减小方向外推得到本征非线性系数Q0(ω):
| $ {Q_0}\left( \omega \right) \equiv \mathop {\lim }\limits_{{\gamma _0} \to 0} \frac{{{I_{3/1}}\left( {\omega , {\gamma _0}} \right)}}{{\gamma _0^2}} $ | (16) |
类比动态模量主曲线,通过采集不同ω下的Q0(ω),可构建得到Q0(ω)主曲线(见图 9(d))。
Q0(ω)主曲线能描述梳型聚合物的分层级松弛现象。Q0(ω)值依赖于分子量、分子量分布和聚合物拓扑结构[96]。线性链的Q0(ω)主曲线从低频到高频先升高后降低,存在一个最大值,其低频末端的Q0(ω)与ω理论上存在如式(17)所示的二次幂的标度关系 [104],实验结果也证明了这种关系的存在(见图 10) [95]。
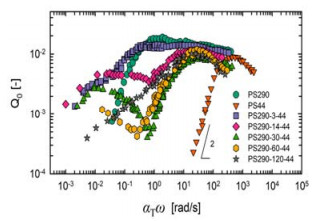
|
图 10 梳型聚苯乙烯本征非线性系数Q0(ω)主曲线[95] Fig.10 Master curve of the intrinsic nonlinear coefficient Q0(ω) of comb polystyrene [95] |
| $ \mathop {\lim }\limits_{\omega \to 0} {Q_0}\left( \omega \right) \propto {\omega ^2} $ | (17) |
对于梳型聚合物,其Q0(ω)主曲线出现两个峰,两峰之间存在一最小值,对应链的松弛变化。Kempf等[88]研究发现高频峰、中频谷、低频峰分别对应侧链松弛、主链Rouse松弛和主链末端松弛,频率的倒数分别对应侧链松弛时间、主链Rouse松弛时间和爬行松弛时间。Song等[95]研究了不同接枝密度的单分散PS-g-PS (Zbb=20、Zsc=3、q=0~190)的Q0(ω)主曲线(图 10),随着分子量增加,峰向低频方向移动,主链松弛时间延长,LC、DC等PS-g-PS呈现两个峰一个谷,高频峰位置都叠加在一起,代表了侧链的松弛;中间谷位置是主链和侧链的过渡区域,标志着主链构象发生了变化;LC和DC的梳型聚苯乙烯的低频峰向低频方向移动,且Q0(ω)变小,表示主链的松弛;当构象为LB时(见图中PS290-120-44),只有一个高频峰存在,低频处的Q0(ω)为ω的单调函数,呈现线性链的特征,此时主链伸展,梳型聚苯乙烯可被看作半径增厚的柔性线性链。
目前仅有傅里叶变换流变对梳型聚合物接枝密度的报道,暂时没有傅里叶变换流变对梳型聚合物主、侧链长度的研究报道,相关的规律还需进行深入的理论和实验研究。
4 结论和展望本文综述了梳型聚合物主、侧链长度和支链数对其构象及流变性能的影响。基于管模型理论和粗粒度分子动力学模拟可区分梳型高分子的四种构象,利用模型分析可获得其平台模量与主链体积分数之间的规律,借助零切黏度、动态模量主曲线、vGP图和傅里叶变换流变等,可定性或定量地表征梳型高分子的链结构,理论与实验结果一致,对梳型聚合物流变研究具有通用性,可以推广到其他链结构清晰的梳型聚合物体系。总结发现,梳型聚合物独特的流变现象是由其侧链带来的链构象变化所导致的,侧链起到了3方面作用:(1)屏蔽主链对黏度的贡献;(2)使主链伸展,从无规高斯构象变为伸展构象;(3)稀释主链的体积分数。这3方面共同作用导致梳型聚合物熔体的零切黏度随侧链增多而下降,甚至低于线性链。链构象变化在动态模量主曲线上呈现明显的分层级松弛现象,高频区域对应聚合物链段松弛,中频平台区域对应侧链松弛,而低频末端则对应主链松弛;随着接枝密度的提高,整个聚合物分子逐渐遵从Rouse松弛机制。vGP图和傅里叶变换流变表征结果也可很好地说明梳型聚合物链的松弛过程。
虽然流变工具用来分析梳型聚合物链结构非常灵敏,相关理论也得到了一些实验结果的验证,但对其链结构的分析目前还停留在半定量阶段,主要依靠已知链结构的模型聚合物来了解流变性能。通过流变性能来反推链结构,往往存在较大偏差,目前仍存在巨大挑战,为此还需:(1)加强相关的流变理论基础研究,建立梳型聚合物流变性能与其链结构的构效关系,包括进一步完善管模型,建立更加准确、通用的流变模型;(2)结合其他链结构分析手段,如核磁、凝胶渗透色谱等,精确分析梳型聚合物链结构,辅助其流变性能研究,相互佐证实验结果;(3)逐步建立相应的大数据库,将梳型聚合物链结构因子与其重要流变性能参数进行关联,使其流变性能参数与链结构因子相对应。
拥有低平台模量和良好流动性的梳型聚合物,在药物载体、润滑剂、刺激响应材料、超柔介电弹性体等方面具有很大的应用潜力,如何设计和优化链结构、定制具有良好流变和力学性能的梳型聚合物,并拓展其在不同领域的应用是梳型聚合物研究所需关注的。目前,梳型聚合物侧链均接枝在一维主链上,如能结合二维材料并在二维平面上接枝侧链,构造出大面积二维平面分子刷;或在球表面接枝长链,构建出三维球形分子刷,并研究它们的流变行为,对开发具有特殊功能的新材料非常重要。
| [1] |
ROOVERS J. Synthesis and dilute-solution characterization of comb polystyrenes[J]. Polymer, 1979, 20(7): 843-849. DOI:10.1016/0032-3861(79)90121-6 |
| [2] |
STADLER F J, ARIKAN-CONLEY B A, KASCHTA J, et al. Synthesis and characterization of novel ethylene-graft-ethylene/ propylene copolymers[J]. Macromolecules, 2011, 44(12): 5053-5063. DOI:10.1021/ma200588r |
| [3] |
LIANG H, GREST G S, DOBRYNIN A V. Brush-like polymers and entanglements: from linear chains to filaments[J]. ACS Macro Letters, 2019, 8(10): 1328-1333. DOI:10.1021/acsmacrolett.9b00519 |
| [4] |
XIE G, MARTINEZ M R, OLSZEWSKI M, et al. Molecular bottlebrushes as novel materials[J]. Biomacromolecules, 2019, 20(1): 27-54. DOI:10.1021/acs.biomac.8b01171 |
| [5] |
VATANKHAH-VARNOOSFADERANI M, DANIEL W F, ZHUSHMA A P, et al. Bottlebrush elastomers: A new platform for freestanding electroactuation[J]. Advanced Materials, 2017, 29(2): 1604209. DOI:10.1002/adma.201604209 |
| [6] |
RIAZI K, KUBEL J, ABBASI M, et al. Polystyrene comb architectures as model systems for the optimized solution electrospinning of branched polymers[J]. Polymer, 2016, 104: 240-250. DOI:10.1016/j.polymer.2016.05.032 |
| [7] |
FENG C, LI Y, YANG D, et al. Well-defined graft copolymers: From controlled synthesis to multipurpose applications[J]. Chemical Society Reviews, 2011, 40(3): 1282-1295. DOI:10.1039/B921358A |
| [8] |
REYNOLDS V G, MUKHERJEE S, XIE R X, et al. Super-soft solvent-free bottlebrush elastomers for touch sensing[J]. Materials Horizons, 2020, 7(1): 181-187. DOI:10.1039/C9MH00951E |
| [9] |
ARRINGTON K J, RADZINSKI S C, DRUMMEY K J, et al. Reversibly cross-linkable bottlebrush polymers as pressure-sensitive adhesives[J]. ACS Applied Materials & Interfaces, 2018, 10(31): 26662-26668. |
| [10] |
ABBASI M, FAUST L, WILHELM M. Molecular origin of the foam structure in model linear and comb polystyrenes: II. Volume expansion ratio[J]. Polymer, 2020, 193: 122354. DOI:10.1016/j.polymer.2020.122354 |
| [11] |
ABBASI M, FAUST L, WILHELM M. Molecular origin of the foam structure in model linear and comb polystyrenes: I cell density[J]. Polymer, 2020, 193: 122351. DOI:10.1016/j.polymer.2020.122351 |
| [12] |
ABBASI M, FAUST L, RIAZI K, et al. Linear and extensional rheology of model branched polystyrenes: From loosely grafted combs to bottlebrushes[J]. Macromolecules, 2017, 50(15): 5964-5977. DOI:10.1021/acs.macromol.7b01034 |
| [13] |
PAKULA T, ZHANG Y, MATYJASZEWSKI K, et al. Molecular brushes as super-soft elastomers[J]. Polymer, 2006, 47(20): 7198-7206. DOI:10.1016/j.polymer.2006.05.064 |
| [14] |
LIANG H Y, MORGAN B J, XIE G J, et al. Universality of the entanglement plateau modulus of comb and bottlebrush polymer melts[J]. Macromolecules, 2018, 51(23): 10028-10039. DOI:10.1021/acs.macromol.8b01761 |
| [15] |
NEARY W J, FULTZ B A, KENNEMUR J G. Well-defined and precision-grafted bottlebrush polypentenamers from variable temperature ROMP and ATRP[J]. ACS Macro Letters, 2018, 7(9): 1080-1086. DOI:10.1021/acsmacrolett.8b00576 |
| [16] |
SHANMUGAM S, CUTHBERT J, KOWALEWSKI T, et al. Catalyst-free selective photoactivation of RAFT polymerization: A facile route for preparation of comblike and bottlebrush polymers[J]. Macromolecules, 2018, 51(19): 7776-7784. DOI:10.1021/acs.macromol.8b01708 |
| [17] |
NEUGEBAUER D, ZHANG Y, PAKULA T, et al. Densely-grafted and double-grafted PEO brushes via ATRP. A route to soft elastomers[J]. Macromolecules, 2003, 36(18): 6746-6755. DOI:10.1021/ma0345347 |
| [18] |
HUANG K, RZAYEV J. Well-defined organic nanotubes from multicomponent bottlebrush copolymers[J]. Journal of the American Chemical Society, 2009, 131(19): 6880-6885. DOI:10.1021/ja901936g |
| [19] |
XIA Y, KORNFIELD J A, GRUBBS R H. Efficient synthesis of narrowly dispersed brush polymers via living ring-opening metathesis polymerization of macromonomers[J]. Macromolecules, 2009, 42(11): 3761-3766. DOI:10.1021/ma900280c |
| [20] |
NIAN S F, LIAN H D, GONG Z H, et al. Molecular architecture directs linear-bottlebrush-linear triblock copolymers to self-assemble to soft reprocessable elastomers[J]. ACS Macro Letters, 2019, 8(11): 1528-1534. DOI:10.1021/acsmacrolett.9b00721 |
| [21] |
CAI L H, KODGER T E, GUERRA R E, et al. Soft poly (dimethylsiloxane) elastomers from architecture-driven entanglement free design[J]. Advanced Materials, 2015, 27(35): 5132-5140. DOI:10.1002/adma.201502771 |
| [22] |
BERNARD J, FAVIER A, DAVIS T P, et al. Synthesis of poly(vinyl alcohol) combs via MADIX/RAFT polymerization[J]. Polymer, 2006, 47(4): 1073-1080. DOI:10.1016/j.polymer.2005.12.004 |
| [23] |
COSTANZO S, SCHERZ L, FLOUDAS G, et al. Hybrid dendronized polymers as molecular objects: Viscoelastic properties in the melt[J]. Macromolecules, 2019, 52(19): 7331-7342. DOI:10.1021/acs.macromol.9b01412 |
| [24] |
COSTANZO S, SCHERZ L F, SCHWEIZER T, et al. Rheology and packing of dendronized polymers[J]. Macromolecules, 2016, 49(18): 7054-7068. DOI:10.1021/acs.macromol.6b01311 |
| [25] |
ZHANG K, LIU P, WANG W J, et al. Preparation of comb-shaped polyolefin elastomers having ethylene/1-octene copolymer backbone and long chain polyethylene branches via a tandem metallocene catalyst system[J]. Macromolecules, 2018, 51(21): 8790-8799. DOI:10.1021/acs.macromol.8b01711 |
| [26] |
LIN T P, CHANG A B, CHEN H Y, et al. Control of grafting density and distribution in graft polymers by living ring-opening metathesis copolymerization[J]. Journal of the American Chemical Society, 2017, 139(10): 3896-3903. DOI:10.1021/jacs.7b00791 |
| [27] |
XU Y W, WANG W Y, WANG Y Y, et al. Fluorinated bottlebrush polymers based on poly(trifluoroethyl methacrylate): Synthesis and characterization[J]. Polymer Chemistry, 2016, 7(3): 680-688. DOI:10.1039/C5PY01514F |
| [28] |
HU M, XIA Y, DAEFFLER C S, et al. The linear rheological responses of wedge-type polymers[J]. Journal of Polymer Science Part B-Polymer Physics, 2015, 53(13): 899-906. DOI:10.1002/polb.23716 |
| [29] |
CHANG A B, LIN T P, THOMPSON N B, et al. Design, synthesis and self-assembly of polymers with tailored graft distributions[J]. Journal of the American Chemical Society, 2017, 139(48): 17683-17693. DOI:10.1021/jacs.7b10525 |
| [30] |
QIAN Z Y, KOH Y P, PALLAKA M R, et al. Linear rheology of a series of second-generation dendronized wedge polymers[J]. Macromolecules, 2019, 52(5): 2063-2074. DOI:10.1021/acs.macromol.8b02122 |
| [31] |
VERDUZCO R, LI X, PESEK S L, et al. Structure, function, self-assembly and applications of bottlebrush copolymers[J]. Chemical Society Reviews, 2015, 44(8): 2405-2420. DOI:10.1039/C4CS00329B |
| [32] |
SHEIKO S S, SUMERLIN B S, MATYJASZEWSKI K. Cylindrical molecular brushes: Synthesis, characterization and properties[J]. Progress in Polymer Science, 2008, 33(7): 759-785. DOI:10.1016/j.progpolymsci.2008.05.001 |
| [33] |
TU S D, CHOUDHURY C K, LUZINOV I, et al. Recent advances towards applications of molecular bottlebrushes and their conjugates[J]. Current Opinion in Solid State & Materials Science, 2019, 23(1): 50-61. |
| [34] |
WANG Y, WENG F, LI J, et al. Influence of phase separation on performance of graft acrylic pressure-sensitive adhesives with various copolyester side chains[J]. ACS Omega, 2018, 3(6): 6945-6954. DOI:10.1021/acsomega.8b00737 |
| [35] |
WANG Y, XIA M, KONG X, et al. Tailoring chain structures of L-lactide and Ε-caprolactone copolyester macromonomers using rac-binaphthyl-diyl hydrogen phosphate-catalyzed ring-opening copolymerization with monomer addition strategy[J]. RSC Advances, 2017, 7(46): 28661-28669. DOI:10.1039/C7RA05531E |
| [36] |
LIU P W, YE Z B, WANG W J, et al. Synthesis of polyethylene and polystyrene miktoarm star copolymers using an "in-out" strategy[J]. Polymer Chemistry, 2014, 5(18): 5443-5452. DOI:10.1039/C4PY00622D |
| [37] |
LIU P W, LANDRY E, YE Z B, et al. "Arm-first" synthesis of core-cross-linked multiarm star polyethylenes by coupling palladium-catalyzed ethylene "living" polymerization with atom-transfer radical polymerization[J]. Macromolecules, 2011, 44(11): 4125-4139. DOI:10.1021/ma2003954 |
| [38] |
ABBASI M, FAUST L, WILHELM M. Comb and bottlebrush polymers with superior rheological and mechanical properties[J]. Advanced Materials, 2019, 31(26): 1806484. DOI:10.1002/adma.201806484 |
| [39] |
LITVINOV V M, RIES M E, BAUGHMAN T W, et al. Chain entanglements in polyethylene nelts. Why is it studied again?[J]. Macromolecules, 2013, 46(2): 541-547. DOI:10.1021/ma302394j |
| [40] |
RAJU V R, SMITH G G, MARIN G, et al. Properties of amorphous and crystallizable hydrocarbon polymers. I. Melt rheology of fractions of linear polyethylene[J]. Journal of Polymer Science: Polymer Physics Edition, 1979, 17(7): 1183-1195. DOI:10.1002/pol.1979.180170704 |
| [41] |
AGUILAR M, VEGA J F, SANZ E, et al. New aspects on the rheological behaviour of metallocene catalysed polyethylenes[J]. Polymer, 2001, 42(24): 9713-9721. DOI:10.1016/S0032-3861(01)00518-3 |
| [42] |
LIANG H, CAO Z, WANG Z, et al. Combs and bottlebrushes in a melt[J]. Macromolecules, 2017, 50(8): 3430-3437. DOI:10.1021/acs.macromol.7b00364 |
| [43] |
PATUREJ J, SHEIKO S S, PANYUKOV S, et al. Molecular structure of bottlebrush polymers in melts[J]. Science Advances, 2016, 2(11): e1601478. DOI:10.1126/sciadv.1601478 |
| [44] |
DANIEL W F, BURDYNSKA J, VATANKHAH-VARNOOSFADERANI M, et al. Solvent-free, supersoft and superelastic bottlebrush melts and networks[J]. Nature Materials, 2016, 15(2): 183-189. DOI:10.1038/nmat4508 |
| [45] |
LIANG H Y, WANG Z L, DOBRYNIN A V. Scattering from melts of combs and bottlebrushes: Molecular dynamics simulations and theoretical study[J]. Macromolecules, 2019, 52(15): 5555-5562. DOI:10.1021/acs.macromol.9b01034 |
| [46] |
LIANG H, WANG Z, SHEIKO S S, et al. Comb and bottlebrush graft copolymers in a melt[J]. Macromolecules, 2019, 52(10): 3942-3950. DOI:10.1021/acs.macromol.9b00611 |
| [47] |
LIANG H, SHEIKO S S, DOBRYNIN A V. Supersoft and hyperelastic polymer networks with brushlike strands[J]. Macromolecules, 2018, 51(2): 638-645. DOI:10.1021/acs.macromol.7b02555 |
| [48] |
WATANABE H. Viscoelasticity and dynamics of entangled polymers[J]. Progress in Polymer Science, 1999, 24(9): 1253-1403. DOI:10.1016/S0079-6700(99)00029-5 |
| [49] |
GABRIEL C, MUNSTEDT H. Influence of long-chain branches in polyethylenes on linear viscoelastic flow properties in shear[J]. Rheologica Acta, 2002, 41(3): 232-244. DOI:10.1007/s00397-001-0219-6 |
| [50] |
JANZEN J, COLBY R H. Diagnosing long-chain branching in polyethylenes[J]. Journal of Molecular Structure, 1999, 485: 569-584. |
| [51] |
LARSON R G. Combinatorial rheology of branched polymer melts[J]. Macromolecules, 2001, 34(13): 4556-4571. DOI:10.1021/ma000700o |
| [52] |
KARJALA T P, SAMMLER R L, MANGNUS M A, et al. Detection of low levels of long-chain branching in polydisperse polyethylene materials[J]. Journal of Applied Polymer Science, 2011, 119(2): 636-646. DOI:10.1002/app.32720 |
| [53] |
KARJALA T P, SAMMLER R L, MANGNUS M A, et al. Detection of low levels of long-chain branching in polyolefins [M]. New York: American Institute of Physics, 2008, 1027(1): 342-344.
|
| [54] |
MILNER S T, MCLEISH T C B. Reptation and contour-length fluctuations in melts of linear polymers[J]. Physical Review Letters, 1998, 81(3): 725-728. DOI:10.1103/PhysRevLett.81.725 |
| [55] |
DANIELS D R, MCLEISH T C B, CROSBY B J, et al. Molecular rheology of comb polymer melts. 1. Linear viscoelastic response[J]. Macromolecules, 2001, 34(20): 7025-7033. DOI:10.1021/ma010712p |
| [56] |
DE GENNES P G. Reptation of a polymer chain in the presence of fixed obstacles[J]. The Journal of Chemical Physics, 1971, 55(2): 572-579. DOI:10.1063/1.1675789 |
| [57] |
INKSON N J, GRAHAM R S, MCLEISH T C B, et al. Viscoelasticity of monodisperse comb polymer melts[J]. Macromolecules, 2006, 39(12): 4217-4227. DOI:10.1021/ma060018f |
| [58] |
DALSIN S J, HILLMYER M A, BATES F S. Linear rheology of polyolefin-based bottlebrush polymers[J]. Macromolecules, 2015, 48(13): 4680-4691. DOI:10.1021/acs.macromol.5b01153 |
| [59] |
WIJESINGHE S, PERAHIA D, GREST G S. Polymer topology effects on dynamics of comb polymer melts[J]. Macromolecules, 2018, 51(19): 7621-7628. DOI:10.1021/acs.macromol.8b01449 |
| [60] |
LÓPEZ-BARRÓN C R, BRANT P, EBERLE A P R, et al. Linear rheology and structure of molecular bottlebrushes with short side chains[J]. Journal of Rheology, 2015, 59(3): 865-883. DOI:10.1122/1.4918977 |
| [61] |
LIN Y C, ZHENG J, YAO K, et al. Synthesis and linear rheological property of comb-like styrene-based polymers with a high degree of branch chain[J]. Polymer, 2015, 59: 252-259. DOI:10.1016/j.polymer.2015.01.020 |
| [62] |
HAUGAN I N, MAHER M J, CHANG A B, et al. Consequences of grafting density on the linear viscoelastic behavior of graft polymers[J]. ACS Macro Letters, 2018, 7(5): 525-530. DOI:10.1021/acsmacrolett.8b00116 |
| [63] |
DALSIN S J, HILLMYER M A, BATES F S. Molecular weight dependence of zero-shear viscosity in atactic polypropylene bottlebrush polymers[J]. ACS Macro Letters, 2014, 3(5): 423-427. DOI:10.1021/mz500082h |
| [64] |
ALEXANDRIS S, PEPONAKI K, PETROPOULOU P, et al. Linear viscoelastic response of unentangled polystyrene bottlebrushes[J]. Macromolecules, 2020, 53(10): 3923-3932. DOI:10.1021/acs.macromol.0c00266 |
| [65] |
LÓPEZ-BARRÓN C R, TSOU A H, HAGADORN J R, et al. Highly entangled a-olefin molecular bottlebrushes: Melt structure, linear rheology and interchain friction mechanism[J]. Macromolecules, 2018, 51(17): 6958-6966. DOI:10.1021/acs.macromol.8b01431 |
| [66] |
ROUSE P E. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers[J]. The Journal of Chemical Physics, 1953, 21(7): 1272-1280. DOI:10.1063/1.1699180 |
| [67] |
张凯伦. 串级催化溶液聚合定制梳状聚烯烃热塑性弹性体的研究[D]. 杭州: 浙江大学, 2019. ZHANG K L. Study on tailoring comb-branched polyolefinic thermoplastic elastomers using a tandem solution copolymerization system [D]. Hangzhou: Zhejiang University, 2019. |
| [68] |
QIAN Z, CHEN D, MCKENNA G B. Re-visiting the "consequences of grafting density on the linear viscoelastic behavior of graft polymers"[J]. Polymer, 2020, 186: 121992. DOI:10.1016/j.polymer.2019.121992 |
| [69] |
HU M, XIA Y, MCKENNA G B, et al. Linear rheological response of a series of densely branched brush polymers[J]. Macromolecules, 2011, 44(17): 6935-6943. DOI:10.1021/ma2009673 |
| [70] |
DALSIN S J, RIONS-MAEHREN T G, BEAM M D, et al. Bottlebrush block polymers: quantitative theory and experiments[J]. ACS Nano, 2015, 9(12): 12233-12245. DOI:10.1021/acsnano.5b05473 |
| [71] |
WILLIAMS M L, LANDEL R F, FERRY J D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids[J]. Journal of the American Chemical Society, 1955, 77(14): 3701-3707. DOI:10.1021/ja01619a008 |
| [72] |
TSUKAHARA Y, NAMBA S, IWASA J, et al. Bulk properties of poly(macromonomer)s of increased backbone and branch lengths[J]. Macromolecules, 2001, 34(8): 2624-2629. DOI:10.1021/ma0016937 |
| [73] |
ROOVERS J, GRAESSLEY W W. Melt rheology of some model comb polystyrenes[J]. Macromolecules, 1981, 14(3): 766-773. DOI:10.1021/ma50004a057 |
| [74] |
VLASSOPOULOS D, FYTAS G, LOPPINET B, et al. Polymacromonomers: Structure and dynamics in nondilute solutions, melts and mixtures[J]. Macromolecules, 2000, 33(16): 5960-5969. DOI:10.1021/ma000634q |
| [75] |
BAILLY C, STEPHENNE V, MUCHTAR Z, et al. Linear viscoelastic behavior of densely grafted poly(chloroethyl vinyl ether)-g-polystyrene combs in the melt[J]. Journal of Rheology, 2003, 47(4): 821-827. DOI:10.1122/1.1579688 |
| [76] |
YAVITT B M, GAI Y, SONG D P, et al. High molecular mobility and viscoelasticity of microphase-separated bottlebrush diblock copolymer melts[J]. Macromolecules, 2016, 50(1): 396-405. |
| [77] |
ZIMM B H. Dynamics of polymer molecules in dilute solution-viscoelasticity, flow birefringence and dielectric loss[J]. Journal of Chemical Physics, 1956, 24(2): 269-278. DOI:10.1063/1.1742462 |
| [78] |
CAO Z, DANIEL W F M, VATANKHAH-VARNOSFADERANI M, et al. Dynamics of bottlebrush networks[J]. Macromolecules, 2016, 49(20): 8009-8017. DOI:10.1021/acs.macromol.6b01358 |
| [79] |
CAO Z, CARRILLO J M Y, SHEIKO S S, et al. Computer simulations of bottle brushes: From melts to soft networks[J]. Macromolecules, 2015, 48(14): 5006-5015. DOI:10.1021/acs.macromol.5b00682 |
| [80] |
FETTERS L J, LOHSE D J, GARCÍA-FRANCO C A, et al. Prediction of melt state poly(a-olefin) rheological properties: The unsuspected role of the average molecular weight per backbone bond[J]. Macromolecules, 2002, 35(27): 10096-10101. DOI:10.1021/ma025659z |
| [81] |
TRINKLE S, FRIEDRICH C. Van gurp-palmen-plot: A way to characterize polydispersity of linear polymers[J]. Rheologica Acta, 2001, 40(4): 322-328. DOI:10.1007/s003970000137 |
| [82] |
GARCÍA-FRANCO C A, LOHSE D J, ROBERTSON C G, et al. Relative quantification of long chain branching in essentially linear polyethylenes[J]. European Polymer Journal, 2008, 44(2): 376-391. DOI:10.1016/j.eurpolymj.2007.10.030 |
| [83] |
QIAN Z Y, MCKENNA G B. Expanding the application of the van gurp-palmen plot: New insights into polymer melt rheology[J]. Polymer, 2018, 155: 208-217. DOI:10.1016/j.polymer.2018.09.036 |
| [84] |
TRINKLE S, WALTER P, FRIEDRICH C. Van gurp-palmen plot ii-classification of long chain branched polymers by their topology[J]. Rheologica Acta, 2002, 41(1/2): 103-113. |
| [85] |
WOOD-ADAMS P M, DEALY J M, DEGROOT A W, et al. Effect of molecular structure on the linear viscoelastic behavior of polyethylene[J]. Macromolecules, 2000, 33(20): 7489-7499. DOI:10.1021/ma991533z |
| [86] |
GARCÍA-FRANCO C A, HARRINGTON B A, LOHSE D J. Effect of short-chain branching on the rheology of polyolefins[J]. Macromolecules, 2006, 39(7): 2710-2717. DOI:10.1021/ma052581o |
| [87] |
DOI Y, MATSUBARA K, OHTA Y, et al. Melt rheology of ring polystyrenes with ultrahigh purity[J]. Macromolecules, 2015, 48(9): 3140-3147. DOI:10.1021/acs.macromol.5b00076 |
| [88] |
KEMPF M, AHIRWAL D, CZIEP M, et al. Synthesis and linear and nonlinear melt rheology of well-defined comb architectures of PS and PpMS with a low and controlled degree of long-chain branching[J]. Macromolecules, 2013, 46(12): 4978-4994. DOI:10.1021/ma302033g |
| [89] |
LEE J H, FETTERS L J, ARCHER L A, et al. Tube dynamics in binary polymer blends[J]. Macromolecules, 2005, 38(9): 3917-3932. DOI:10.1021/ma040080h |
| [90] |
PARK S J, LARSON R G. Tube dilation and reptation in binary blends of monodisperse linear polymers[J]. Macromolecules, 2004, 37(2): 597-604. DOI:10.1021/ma0343683 |
| [91] |
WATANABE H, ISHIDA S, MATSUMIYA Y, et al. Test of full and partial tube dilation pictures in entangled blends of linear polyisoprenes[J]. Macromolecules, 2004, 37(17): 6619-6631. DOI:10.1021/ma0495689 |
| [92] |
VAN RUYMBEKE E, SHCHETNIKAVA V, MATSUMIYA Y, et al. Dynamic dilution effect in binary blends of linear polymers with well-separated molecular weights[J]. Macromolecules, 2014, 47(21): 7653-7665. DOI:10.1021/ma501566w |
| [93] |
WILHELM M. Fourier-transform rheology[J]. Macromolecular Materials and Engineering, 2002, 287(2): 83-105. DOI:10.1002/1439-2054(20020201)287:2<83::AID-MAME83>3.0.CO;2-B |
| [94] |
HYUN K, WILHELM M, KLEIN C O, et al. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear(LAOS)[J]. Progress in Polymer Science, 2011, 36(12): 1697-1753. DOI:10.1016/j.progpolymsci.2011.02.002 |
| [95] |
SONG H Y, FAUST L, SON J, et al. Small and medium amplitude oscillatory shear rheology of model branched polystyrene (PS) melts[J]. Polymers (Basel), 2020, 12(2): 365-385. DOI:10.3390/polym12020365 |
| [96] |
CZIEP M A, ABBASI M, HECK M, et al. Effect of molecular weight, polydispersity and monomer of linear homopolymer melts on the intrinsic mechanical nonlinearity 3Q0(Ω) in MAOS[J]. Macromolecules, 2016, 49(9): 3566-3579. DOI:10.1021/acs.macromol.5b02706 |
| [97] |
HYUN K, BAIK E S, AHN K H, et al. Fourier-transform rheology under medium amplitude oscillatory shear for linear and branched polymer melts[J]. Journal of Rheology, 2007, 51(6): 1319-1342. DOI:10.1122/1.2790072 |
| [98] |
VITTORIAS I, WILHELM M. Application of FT rheology to industrial linear and branched polyethylene blends[J]. Macromolecular Materials and Engineering, 2007, 292(8): 935-948. DOI:10.1002/mame.200700120 |
| [99] |
VITTORIAS I, PARKINSON M, KLIMKE K, et al. Detection and quantification of industrial polyethylene branching topologies via fourier-transform rheology, NMR and simulation using the pom-pom model[J]. Rheologica Acta, 2007, 46(3): 321-340. |
| [100] |
SCHLATTER G, FLEURY G, MULLER R. Fourier-transform rheology of branched polyethylene: Experiments and models for assessing the macromolecular architecture[J]. Macromolecules, 2005, 38(15): 6492-6503. DOI:10.1021/ma0505530 |
| [101] |
NEIDHÖFER T, SIOULA S, HADJICHRISTIDIS N, et al. Distinguishing linear from star-branched polystyrene solutions with fourier-transform rheology[J]. Macromolecular Rapid Communications, 2004, 25(22): 1921-1926. DOI:10.1002/marc.200400295 |
| [102] |
HYUN K, AHN K H, LEE S J, et al. Degree of branching of polypropylene measured from fourier-transform rheology[J]. Rheologica Acta, 2006, 46(1): 123-129. DOI:10.1007/s00397-006-0098-y |
| [103] |
AHIRWAL D, FILIPE S, NEUHAUS I, et al. Large amplitude oscillatory shear and uniaxial extensional rheology of blends from linear and long-chain branched polyethylene and polypropylene[J]. Journal of Rheology, 2014, 58(3): 635-658. DOI:10.1122/1.4867555 |
| [104] |
HYUN K, WILHELM M. Establishing a new mechanical nonlinear coefficientqfrom FT-rheology: First investigation of entangled linear and comb polymer model systems[J]. Macromolecules, 2009, 42(1): 411-422. DOI:10.1021/ma8017266 |
| [105] |
KAPNISTOS M, KIRKWOOD K M, RAMIREZ J, et al. Nonlinear rheology of model comb polymers[J]. Journal of Rheology, 2009, 53(5): 1133-1153. DOI:10.1122/1.3191781 |