2. 华东理工大学 化学工程联合国家重点实验室,上海 200237
2. State Key Laboratory of Chemical Engineering, East China University of Science and Technology, Shanghai 200237, China
我国煤炭资源丰富,国家多项政策指明了煤炭行业供给侧改革的发展方向是清洁高效利用[1]。大规模煤制天然气项目已在新疆、内蒙古等富煤地区投产,该工艺中甲烷化反应段对甲烷产率影响最大。副反应中甲烷吸热会产生丝状炭附着在催化剂内孔道表面,长时间的积累会导致催化剂内孔道严重堵塞[2-3]。张沛等[4]采用扫描电子显微镜(SEM)等表征方法,对商用选择性催化还原(SCR)脱硝催化剂的失活和再生进行研究,发现砷和硫酸盐严重堵塞了催化剂微孔道,酸洗再生能有效脱除砷和硫酸盐,提高SCR脱硝催化剂活性。KOO等[5]采用不同Mg/Al混合比控制的载体,提高了甲烷重整制合成气催化剂的抗结焦能力。DEMICHELI等[6-7]在实验中测定了甲烷在Ni/Al2O3催化剂上形成积炭的反应动力学方程,使数值模拟方法研究甲烷化反应积炭过程成为可能。
采用CFD方法对固定床反应器内“三传一反”(动量传递、质量传递、热量传递、化学反应过程[8])规律进行研究能够节省大量的实验和人工成本,并获得反应器内部更详细的特征参数[9-10]。CHEIN等[11]采用数值模拟方法研究了固定床管式反应器中甲烷化反应的影响因素,发现CO甲烷化反应对温度最敏感,提高反应压力和降低空速能提高甲烷产率。SON等[12]采用数值模拟方法研究了操作条件对积炭效应的影响,但模拟也仅停留在反应器宏观尺度和催化剂-流体域介观尺度。对固定床反应器的模拟研究通常将催化剂床层简化为多孔介质模型或者规则排列的小球[13-14],耦合催化剂内和床层流体域的多尺度研究也几乎只在国外文献中报道,DIXON等[15-17]在催化剂内部反应过程的研究中做了很大贡献,但大都针对于蒸汽重整等反应。掌握降低积炭效应的技术,必需建立更趋于真实的随机堆积固定床床层,并将介观流体域和微观催化剂域的多物理场耦合,研究多尺度下甲烷化反应催化剂积炭形成过程。
本文首先使用DEM软件生成颗粒(催化剂)直径dp=0.012 m、床层与颗粒直径比N=4、高径比H/D=5的随机堆积球形颗粒床层,并提取颗粒位置信息,通过编程在CFD软件中建立床层几何模型,将计算域分为床层流体域和催化剂颗粒域,建立“三传一反”多物理场耦合数学模型,通过数值模拟分析了微观颗粒域的积炭形成规律。最后讨论入口温度400、450、500 K,催化剂温度770、810、850 K,入口流速0.005、0.010、0.015 m·s-1和入口氢气占比0、20%、40%分别对甲烷化反应催化剂积炭过程的影响。
2 模型的建立与验证 2.1 几何模型在随机堆积颗粒的固定床反应器中,较大管径比将导致床层颗粒数倍增,给数值求解带来巨大的计算量,而小管径比固定床反应器在强放热、吸热反应和实验室研究阶段应用也比较广泛,两者径向流动均匀性存在差异,但最终整体特征规律仍具有一定相似性。
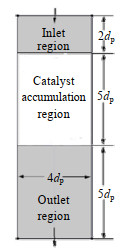
本文建立了小管径比固定床反应器床层,结构如图 1所示,甲烷从上端进入,下端流出,床层总高为12 dp,直径为4 dp,将床层分为入口、催化剂堆积和出口3个区域,入口区域高2 dp,催化剂堆积区域高5 dp,出口区域高5 dp。使用DEM软件在催化剂堆积区域生成直径为dp=12 mm的球型颗粒,并提取颗粒位置信息,建立几何模型如图 2所示,DEM参数设置如表 1。
|
图 1 床层结构示意图 Fig.1 Schematic diagram of the bed structure |

|
图 2 床层堆积模型 Fig.2 Schematic diagram of the bed packing model |
|
|
表 1 DEM参数设置 Table 1 Parameters for DEM |
甲烷化反应在颗粒内放出的热量成为积炭反应热源,颗粒内由无数微孔道组成,现有建模手段和计算能力很难实现颗粒内成千上万微孔道的建模,积炭又覆盖在内孔道表面,改变了催化剂的孔隙率。因此,做出以下合理假设:
(1) 流体为理想气体;
(2) 流体为不可压缩、稳态的层流;
(3) 催化剂颗粒为多孔介质模型;
(4) 反应所需要的热量来自颗粒;
(5) 积炭对催化剂活性的影响非常小可忽略,主要影响孔隙率的变化。
基于以上假设,建立多物理场耦合数学模型,控制方程如下:
(1) 动量守恒方程:
| $\nabla \left( {\varepsilon \rho \boldsymbol{u}} \right) = 0$ | (1) |
| $\frac{{\rm{1}}}{{{\varepsilon ^2}}}\nabla \cdot \left( {\rho \boldsymbol{uu}} \right){\rm{ = }}\nabla \cdot \left( {{\rm{ - }}p \boldsymbol{I} + \frac{\mu }{\varepsilon }\left( {\nabla \boldsymbol{u} + {{\left( {\nabla \boldsymbol{u}} \right)}^{\rm T}}} \right) - \frac{{2\mu }}{{3\varepsilon }}\nabla \boldsymbol{I} \cdot \boldsymbol{u}} \right) - \frac{\mu }{\kappa }\boldsymbol{u}$ | (2) |
式中:I为单位矩阵,▽为梯度算子,μ为动力黏度,Pa·s;混合物密度和平均摩尔质量分别采用如下表达式:
| $\rho {\rm{ = }}\frac{{p{M_{{\rm{ave}}}}}}{{RT}}, M = {\left( {\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{{M_i}}}} } \right)^{ - 1}}$ | (3) |
(2) 能量守恒方程:
| $ \nabla \cdot \left( {\varepsilon \rho {C_p} \boldsymbol{u} \cdot T} \right) = \nabla \cdot \left( {{\lambda _{\rm e}} \cdot \nabla T} \right) + Q $ | (4) |
其中,有效热导率、混合物比热容和各物质的质量分数采用如下表达式:
| ${\lambda _{\rm e}} = \varepsilon {\lambda _{\rm mix}} + \left( {1 - \varepsilon } \right){\lambda _{\rm cat}}, {C_p} = \sum\limits_{i = 1}^n {{w_i}{C_{{p_i}}}} , {w_i} = \frac{{{c_i}{M_i}}}{{\sum\limits_{i = 1}^n {{c_i}{M_i}} }}$ | (5) |
(3) 质量守恒方程:
| $\nabla \cdot \left( {\varepsilon \rho \boldsymbol{u}{w_i} - \rho {w_i}D_i^{\rm m} \cdot \left( {\nabla + \frac{{\nabla {M_{\rm ave}}}}{{{M_{\rm ave}}}}} \right) - \rho {w_i}\sum\limits_{i = 1}^n {\frac{{{M_i}}}{{{M_{\rm ave}}}}} D_i^{\rm m}\nabla {x_i}} \right) = r$ | (6) |
其中,二元混合物扩散系数采用如下表达式:
| $D_i^{\rm m} = \frac{{1 - {w_i}}}{{\sum\limits_{i \ne j} {\frac{{{x_j}}}{{D_{ij}^{\rm e}}}} }}$ | (7) |
合成气甲烷化是强放热反应,副反应中甲烷又会吸热生成炭,反应方程式如下:
| ${\rm C{H_4}\overset {} \longleftrightarrow C + 2{H_2} }\;\;\;\;\Delta {H_{298{\rm K}}}{\rm{ = }}73.7 {\rm kJ \cdot mo{l^{ - 1}}}$ | (8) |
文献[6]给出了Ni/Al2O3催化剂上甲烷积炭反应的动力学方程,表达式如下:
| $r = k\frac{{{p_{\rm C{H_4}}} - p_{{\rm H_2}}^2/{K_{\rm P}}}}{{{{\left( {1 + {K_{\rm H}}\sqrt {{p_{{{\rm H}_2}}}} } \right)}^2}}}$ | (9) |
其中,k、KP和KH的表达式如下:
| $k = {\exp _{}}\left( {20.492 - \frac{{104\;200}}{{RT}}} \right)$ | (10) |
| ${K_{\rm P}} = 5.088 \times {10^5}{\exp _{}}\left( { - \frac{{91\;200}}{{RT}}} \right)$ | (11) |
| ${K_{\rm H}} = {\exp _{}}\left( {\frac{{163\;200}}{{RT}} - 22.426} \right)$ | (12) |
积炭会降低催化剂孔隙率,进而影响渗透率,初始渗透率采用多孔介质Kozeny-Carman渗透率模型,描述催化剂孔隙率和渗透率变化的表达式[18]如下:
| $\frac{{{\rm d}\varepsilon }}{{{\rm d}t}} = - {k_{{\rm{por}}}}\frac{{{\varepsilon _0}r{M_{\rm C}}}}{{{\rho _{\rm depos}}}}$ | (13) |
| $\kappa = {\kappa _0}{\left( {\frac{\varepsilon }{{{\varepsilon _0}}}} \right)^{3.55}}$ | (14) |
| ${\kappa _{\rm{0}}}{\rm{ = }}\frac{{{{(d_{\rm p}^{}\varepsilon _0^{})}^2}}}{{180{{(1 - {\varepsilon _0})}^2}}}$ | (15) |
式中:MC为积炭的摩尔质量,0.012 kg·mol-1;ρdepos为积炭的密度,2 000 kg·m-3。
2.2.3 边界条件与计算方法入口初始甲烷摩尔分数为1,温度为500 K,平均流速为0.015 m·s-1,出口压力为101 325 Pa,将反应源添加在催化剂颗粒域,壁面设置为无滑移和热绝缘边界条件,催化剂区域设置为热源,温度为850 K。催化剂初始孔隙率采用Dixon实验测得的Ni/Al2O3球型催化剂孔隙率0.44[19]。
考虑到多物理场耦合中非线性方程组求解的难度,首先将物理场解耦,单独计算稳态流场,最后将稳态流场与其他物理场耦合计算,采用直接迭代PARDISO算法求解,瞬态求解8 000 s,步长为60 s,使用默认松弛因子值。
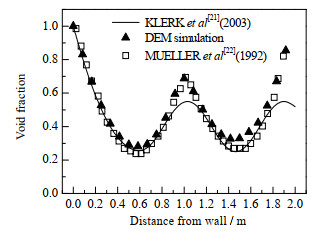
2.3 验证 2.3.1 几何模型准确性验证早期学者提出球型固定床床层整体空隙率[20]与径向空隙率分布[21]的经验公式,并与实验数据吻合较好,得到学者们的广泛认可。
整体空隙率经验公式如下:
| $\varepsilon = 0.4 + 0.05\left( {{d_{\rm p}}/D} \right) + 0.412{\left( {{d_{\rm p}}/D} \right)^2}, {d_{\rm p}}/D \le 0.5$ | (16) |
经计算,本文中DEM堆积的床层整体空隙率为0.47,拟合公式计算空隙率为0.44,相差3%,误差主要来源于堆积的随机性以及计算空隙率时床层高度的取值。
径向空隙率经验公式如下:
| ${\varepsilon _{\rm r}} = 2.14{z^2} - 2.53z + 1, z \le 0.637$ | (17) |
| ${\varepsilon _{\rm r}} = {\varepsilon _{\rm b}} + 0.29\exp \left( { - 0.6z} \right) \cdot \left( {\cos \left( {2.3 \mathsf{π} \left( {z - 0.16} \right)} \right)} \right) + 0.15\exp \left( { - 0.9z} \right), z > 0.637$ | (18) |
式中:

|
图 3 径向空隙率截取示意图 Fig.3 Schematic diagram of the radial void fraction |
|
图 4 径向空隙率与文献对比 Fig.4 Comparison of the radial void fraction results with literature |
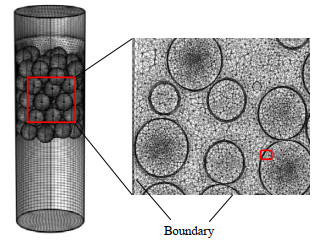
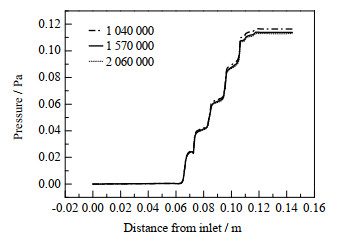
由于反应主要发生在催化剂堆积区,为减少计算量将进出口区域划分为六面体网格,催化剂堆积区均划分为四面体网格,筒体和颗粒边界划分3层边界层。反应、扩散等行为在颗粒域更为复杂,对其网格进行加密处理,由于在颗粒中心施加温度边界,为更精确计算边界处参数,将颗粒中心网格再次细化,网格划分如图 5所示。直接划分网格会导致壁面接触点附近网格质量急剧降低,将所有颗粒直径减小1%,床层空隙率只下降1.2%,对结果影响较小。采用同样的网格划分方法划分1 040 000、1 570 000和2 060 000网格,比较3种网格床层压降变化,如图 6所示,结果表明,继续细化网格对结果并无较大影响,为降低计算成本,将网格数量确定为1 570 000。
|
图 5 网格划分 Fig.5 Mesh generation |
|
图 6 网格数量对压力变化的影响 Fig.6 Effects of grid number on pressure variation |
KUVSHINOV等[23]在填装Ni/Al2O3催化剂,外部持续加热维持等温状态的管式反应器中进行甲烷积碳反应实验,测得H2占比为0、0.15、0.30、0.40时,温度从760 K增加到860 K时,反应速率的变化规律。本文采用CFD方法同样进行等温反应的模拟,将模拟值与文献值对比,如图 7所示,在氢气质量分数为0时,模拟值与试验值有很小的误差,其余参数下二者结果基本吻合,证明模拟方法准确可靠。
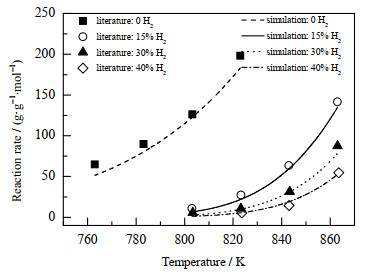
|
图 7 模拟值与实验值对比 Fig.7 Comparison of simulation with experimental values |
将流体域与颗粒域多物理场耦合计算,得到如图 8所示的多物理场分布示意图。从速度流线图可以看出,流体流动在出入口区很稳定,在床层堆积区会沿颗粒表面无规则流动,局部速度会增大到入口流速的10倍,颗粒尾部还会出现尾流和回流现象,流体流经颗粒多孔介质区域,在刚接触颗粒、离开颗粒和颗粒内的速度几乎为0。反应器壁面(右)是压力分布,压降发生在床层堆积区,进出口压降为0.104 Pa。反应器壁面(左)是温度分布,入口甲烷温度为500 K,随着距入口距离的增加,床层区温度逐渐上升,第1层颗粒温度从500 K迅速上升至850 K,到第2层颗粒时温度基本达到850 K。颗粒表面是反应刚开始时甲烷浓度分布,甲烷在颗粒上半部分浓度高,下半部分浓度低,在入口区域浓度为14.4 mol·m-3,底部最小浓度能达到14 mol·m-3。
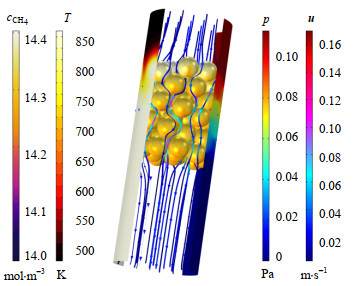
|
图 8 多物理场分布 Fig.8 Multiple physical field distribution |
分别提取了不同时刻床层中心截面温度、甲烷摩尔分数、反应速率和颗粒中心截面孔隙率的分布。图 9为不同时刻床层中心截面温度分布,当t=0 s时,入口温度为500 K,颗粒中心温度为850 K,其他区域温度均为293.15 K。当t=60 s时,各区域温度基本达到稳定,床层堆积区和流体区温度迅速上升至850 K,但由于入口区不断有500 K的甲烷流入,使入口区和床层堆积区产生500~850 K的温度梯度。
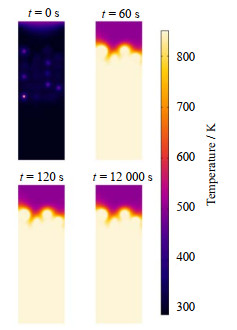
|
图 9 温度随时间的变化 Fig.9 Temperature profiles as a function of time |
图 10为甲烷摩尔分数随时间的变化,当t=60 s时,颗粒内少部分甲烷已经开始反应。当t=2 000 s时,由于甲烷向催化剂内层扩散,扩散阻力增大,部分甲烷反应生成了碳和氢气,甲烷摩尔分数开始减小,最小为0.93;气流方向至上而下,单个颗粒上半部分甲烷供给更快,导致甲烷在颗粒上半部分多、下半部分少。当t=4 000 s时,颗粒内层甲烷摩尔分数最小为0.90,此时外层孔道已经严重堵塞,颗粒内部传质受外部气流影响减小,导致甲烷在颗粒内近似呈圆环状减小。当t=8 000 s时,颗粒几乎完全堵塞,甲烷在颗粒内呈圆环状减小的趋势更明显,不同的是颗粒内层甲烷摩尔分数最小已下降至0.85。
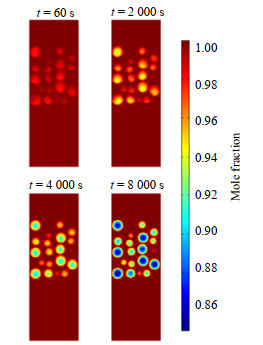
|
图 10 甲烷摩尔分数随时间的变化 Fig.10 Profiles of methane mole fraction as a function of time |
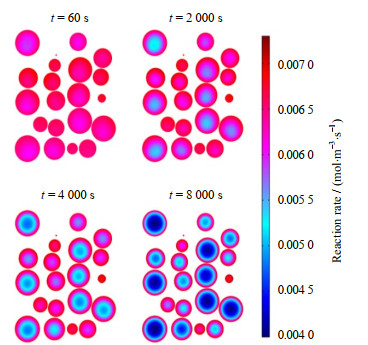
图 11为反应速率随时间的变化,当t=60 s时,最小反应速率为0.006 1 mol·m-3·s-1;当t=2 000 s时,颗粒内甲烷被消耗减少,最小反应速率减小至0.005 3 mol·m-3·s-1;当t=4 000、8 000 s时,最小反应速率分别为0.004 8、0.004 0 mol·m-3·s-1,分布规律同甲烷摩尔分数分布规律相同,反应速率在颗粒内也近乎呈圆环状减小。
|
图 11 反应速率随时间的变化 Fig.11 Variation of reaction rate as a function of time |
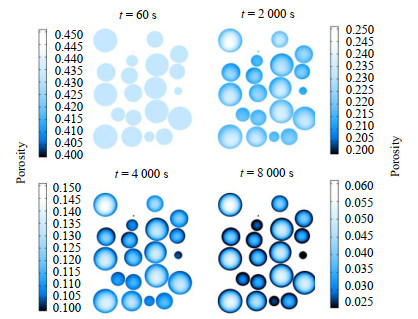
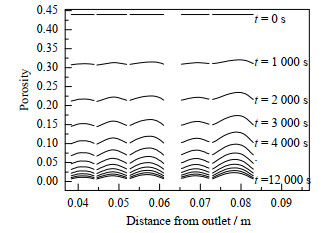
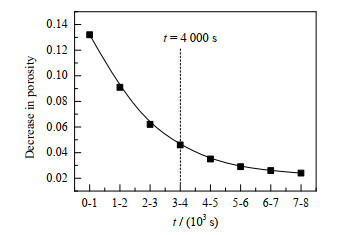
如图 12所示,反应从60 s进行到8 000 s,颗粒内平均孔隙率值从0.44下降到0.04左右。随反应的进行,颗粒外层比内层积炭更严重,当t=4 000 s时,颗粒内、外层孔隙率值最大相差0.05,对比图 12和11,发现反应速率越快的区域,孔隙率越小。提取了相同时间间隔(1 000 s)床层中心轴线上颗粒内的孔隙率分布,如图 13所示,表明反应越充分,颗粒内孔隙率分布越不均匀,呈现出外层低、内层高的规律。提取前8 000 s每1 000 s颗粒内平均孔隙率下降值,如图 14所示,表明孔隙率下降程度随时间的增加在不断减缓,4 000 s前,催化剂未完全堵死,反应剧烈,平均每1 000 s颗粒内平均孔隙率值下降0.08;4 000 s之后,颗粒内平均孔隙率值下降到0.1以下,积炭反应减慢,平均每1 000 s颗粒内平均孔隙率值下降0.025。
|
图 12 中心截面孔隙率随时间的变化 Fig.12 Variation of central section porosity as a function of time |
|
图 13 中心截线孔隙率随时间的变化 Fig.13 Variation of central line porosity as a function of time |
|
图 14 相同时间间隔孔隙率下降趋势 Fig.14 Decrease of porosity under same time intervals |
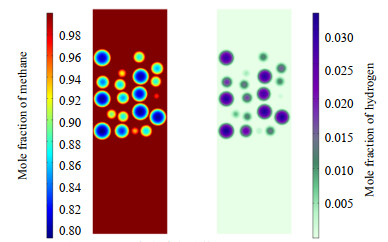
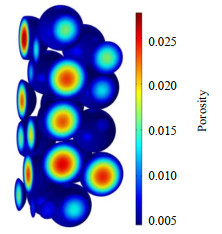
根据3.3节描述,发现时间进行到8 000 s时反应程度已经很小,为增加结论的准确性,将计算时间增加到12 000 s,提取稳态时甲烷、氢气摩尔分数和颗粒内孔隙率分布云图。如图 15所示,当t=12 000 s时,流体区甲烷摩尔分数高达99%,氢气含量很少,从颗粒外层到内层,甲烷含量越来越低,氢气含量越来越高。如图 16所示,当t=12 000 s时颗粒内平均孔隙率值为0.015,此时颗粒内、外层孔隙率值相差0.02,颗粒外层积炭仍然更严重。这种现象是颗粒内扩散和反应同时造成的,颗粒外层反应速率大,生成的氢气和碳也越多,同时大量甲烷也会稀释氢气,使颗粒外层的氢气减少;颗粒内层甲烷内扩散的同时也不断地反应产生氢气,最后集中在颗粒中心,内层反应程度反而越来越小,积炭程度也越来越小。
|
图 15 甲烷和氢气摩尔分数对比(t = 12 000 s) Fig.15 Comparison of mole fraction of methane and hydrogen (t = 12 000 s) |
|
图 16 孔隙率分布(t = 12 000 s) Fig.16 Porosity distribution (t = 12 000 s) |
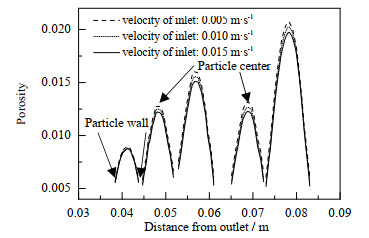
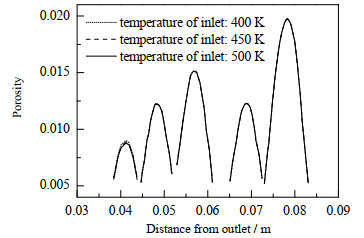
实际生产中,最容易控制的是操作参数,且通过改变操作参数来提高生产效率经济成本最低。由图 16可知,每一个颗粒内孔隙率分布都表现出对称性,表明颗粒中心截线上孔隙率的变化能够反映颗粒内平均孔隙率的变化规律。因此,提取当t=12 000 s,稳态时,床层中心轴线上颗粒内孔隙率的变化,研究了不同入口氢气占比、温度、流速和催化剂温度对积炭效应的影响,如图 17~20所示。
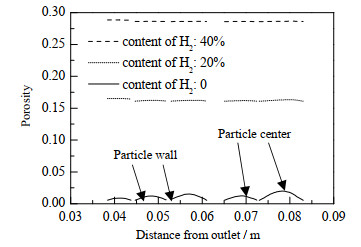
|
图 17 入口氢气含量对孔隙率的影响 Fig.17 Effects of inlet hydrogen contents on porosity |
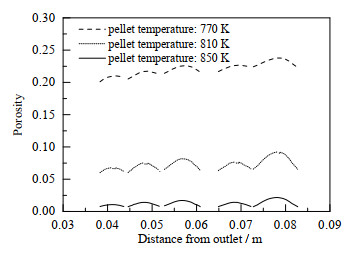
|
图 18 催化剂温度对孔隙率的影响 Fig.18 Effects of catalyst temperature on porosity |
|
图 19 入口速度对孔隙率的影响 Fig.19 Effects of inlet velocities on porosity |
|
图 20 入口温度对孔隙率的影响 Fig.20 Effects of inlet temperature on porosity |
如图 17所示,入口组分无氢气时,颗粒内平均孔隙率值为0.02,积碳非常严重,加入氢气,由于增加了生成物使促使反应逆向进行,颗粒内平均孔隙率值明显提高;当氢气占比40%时,颗粒内平均孔隙率值增大到0.29,同时,加入氢气会使颗粒内、外层甲烷浓度梯度减小,积炭分布越均匀。如图 18所示,颗粒内温度为770 K时,颗粒内平均孔隙率值为0.23;温度从770 K上升到810 K,颗粒内平均孔隙率下降约0.15;温度从810 K升高到850 K,颗粒内平均孔隙率值下降约0.06,表明催化剂升温会加速积炭的形成,继续升温对积炭的影响越来越小。如图 19所示,入口速度从0.005 m·s-1增加到0.010、0.015 m·s-1对颗粒内平均孔隙率几乎无影响,但颗粒中心处孔隙率值会下降0.001左右,这是由于增大流速会增大反应器轴向压差,在更大压力驱动下相同时间甲烷内扩散越多,生成的积炭也越多。如图 20所示,入口温度的升高只导致第一层颗粒中心的孔隙率减小,因为入口温度越高,进入床层的气体能够更快达到反应区温度,更快生成积炭。这与温度场分布规律一致,由图 10可知,第1层颗粒温度变化梯度较大,第2层温度基本达到稳定。
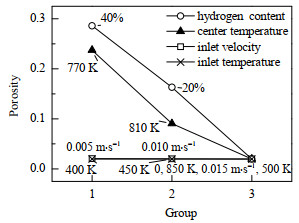
图 21更直观的反应了4种操作参数对颗粒内平均孔隙率的影响,入口氢气从0增加到40%,颗粒内平均孔隙率值从0.02上升至0.29,增加了0.27。催化剂温度从770 K增加到850 K,颗粒内平均孔隙率值从0.24变为0.02,减小了0.22。当入口流速从0.005 m·s-1增加到0.015 m·s-1时,颗粒中心孔隙率减小0.01,平均孔隙率几乎无变化。当入口温度从400 K增加到500 K,第1层颗粒中心孔隙率减小0.005,其他颗粒中心、平均孔隙率均无变化。
|
图 21 孔隙率的影响对比(t = 12 000 s) Fig.21 Comparison of effects of different factors on porosity (t = 12 000 s) |
建立随机堆积球形催化剂固定床床层几何模型和甲烷化反应积炭过程的多物理场有限元模型,模拟了床层介尺度流体域和微尺度颗粒域的“三传一反”现象,解析了催化剂内部积炭形成过程,并讨论不同操作参数对积炭效应的影响,得到以下结论:
(1) 以模拟的方法揭示了积炭是由催化剂外层到内层逐渐形成的,积碳主要发生在反应初期,最先产生在催化剂外表面,积炭发生在内孔道表面相对滞后,导致颗粒内孔隙率从外到内呈圆环状减小:
① 当t=4 000 s时,颗粒内、外层孔隙率值最大相差0.05;
② 当t=0 s时,催化剂孔隙率值为0.44,反应进行4 000 s时减小至0.1,8 000 s减小至0.025。
(2) 研究了不同操作参数对积炭效应的影响,发现增加入口氢气含量、降低催化剂温度能明显降低积炭效应,降低入口流速和入口温度能轻微减缓催化剂中心积炭程度:
① 当入口氢气从0增加到40%时,颗粒内平均孔隙率值增大0.27;
② 当催化剂温度从770 K增加到850 K时,颗粒内平均孔隙率值减小0.22;
③ 当入口流速从0.005 m·s-1增加到0.015 m·s-1时,每层催化剂中心孔隙率值减小0.01;
④ 当入口温度从400 K增加到500 K时,第1层催化剂中心孔隙率值减小0.005。
符号说明:
|
|
| [1] |
谢和平, 王金华, 鞠杨. 煤炭革命的战略与方向[M]. 北京: 科学出版社, 2018. XIE H P, WANG J H, JU Y. Coal industry reform:Strategies and directions[M]. Beijing: Science Press, 2018. |
| [2] |
SCHLERETH D, HINRICHSEN O. A fixed-bed reactor modeling study on the methanation of CO2[J]. Chemical Engineering Research and Design, 2014, 92(4): 702-712. DOI:10.1016/j.cherd.2013.11.014 |
| [3] |
NISHII H, MIYAMOTO D, UMEDA Y, et al. Catalytic activity of several carbons with different structures for methane decomposition and by-produced carbons[J]. Applied Surface Science, 2019, 473: 291-297. DOI:10.1016/j.apsusc.2018.12.073 |
| [4] |
张沛, 吴思明, 方拓拓, 等. 660MW燃煤电厂商用SCR催化剂的失活与再生[J]. 高校化学工程学报, 2017, 31(5): 1186-1192. ZHANG P, WU S M, FANG T T, et al. Deactivation and regeneration of commercial SCR catalysts used in a 660 MW coal-fired power plant[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(5): 1186-1192. DOI:10.3969/j.issn.1003-9015.2017.05.023 |
| [5] |
KOO K Y, ROH H S, JUNG U H, et al. Combined H2O and CO2 reforming of CH4 over nano-sized Ni/MgO-Al2O3 catalysts for synthesis gas production for gas to liquid (GTL):Effect of Mg/Al mixed ratio on coke formation[J]. Catalysis Today, 2009, 146(1/2): 166-171. |
| [6] |
DEMICHELI M C, PONZI E N, FERRETTI O A, et al. Kinetics of carbon formation from CH4-H2 mixtures on nickel-alumina catalyst[J]. The Chemical Engineering Journal, 1991, 46(3): 129-136. DOI:10.1016/0300-9467(91)87004-T |
| [7] |
KUVSHINOV G G, MOGILNYKH Y I, KUVSHINOV D G. Kinetics of carbon formation from CH4-H2 mixtures over a nickel containing catalyst[J]. Catalysis Today, 1998, 42(3): 357-360. DOI:10.1016/S0920-5861(98)00115-1 |
| [8] |
陈甘棠. 化学反应工程[M]. 北京: 化学工业出版社, 2007. CHEN G T. Chemical reaction engineering[M]. Beijing: Chemical Industry Press, 2007. |
| [9] |
DIXON A G, NIJEMEISLAND M. CFD as a design tool for fixed-bed reactors[J]. Industrial & Engineering Chemistry Research, 2001, 40(23): 5246-5254. |
| [10] |
白晓波, 王胜, 任富强, 等. 合成气完全甲烷化固定床反应器数值模拟[J]. 高校化学工程学报, 2015, 29(4): 955-962. BAI X B, WANG S, REN F Q, et al. Numerical simulation of a fixed-bed reactor for total methanation of syngas[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(4): 955-962. DOI:10.3969/j.issn.1003-9015.2015.04.025 |
| [11] |
CHEIN R Y, YU C T, WANG C C. Numerical simulation on the effect of operating conditions and syngas compositions for synthetic natural gas production via methanation reaction[J]. Fuel, 2016, 185: 394-409. DOI:10.1016/j.fuel.2016.07.123 |
| [12] |
SON I H, LEE S J, SOON A, et al. Steam treatment on Ni/γ-Al2O3 for enhanced carbon resistance in combined steam and carbon dioxide reforming of methane[J]. Applied Catalysis B:Environmental, 2013, 134-135: 103-109. DOI:10.1016/j.apcatb.2013.01.001 |
| [13] |
俞路, 刘响, 宋小沫, 等. 固定床反应器甲醇制烯烃反应过程的CFD模拟[J]. 高校化学工程学报, 2016, 30(5): 1095-1103. YU L, LIU X, SONG X M, et al. CFD modeling of methanol-to-olefin processes in fixed bed reactors[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(5): 1095-1103. DOI:10.3969/j.issn.1003-9015.2016.05.016 |
| [14] |
程源洪, 张亚新, 王吉德, 等. 甲烷化固定床反应器床层反应过程与场分布数值模拟[J]. 化工学报, 2015, 66(9): 3391-3397. CHENG Y H, ZHANG Y X, WANG J D, et al. Numerical analysis of reaction process and flow field in fixed bed of methanation reactor[J]. CIESC Journal, 2015, 66(9): 3391-3397. |
| [15] |
DIXON A G. Local transport and reaction rates in a fixed bed reactor tube:Endothermic steam methane reforming[J]. Chemical Engineering Science, 2017, 168: 156-177. DOI:10.1016/j.ces.2017.04.039 |
| [16] |
DIXON A G, TASKIN M E, NIJEMEISLAND M. CFD method to couple three-dimensional transport and reaction inside catalyst particles to the fixed bed flow field[J]. Industrial & Engineering Chemistry Research, 2010, 49(19): 9012-9025. |
| [17] |
PARTOPOUR B, DIXON A G. Computationally efficient incorporation of microkinetics into resolved-particle CFD simulations of fixed-bed reactors[J]. Computers & Chemical Engineering, 2016, 88: 126-134. |
| [18] |
BORISOVA E A, ADLER P M. Deposition in porous media and clogging on the field scale[J]. Physical Review E, 2005, 71(1): 16-31. |
| [19] |
TASKIN E, TROUPEL A, DIXON A G. Flow, transport, and reaction interactions for cylindrical particles with strongly endothermic reactions[J]. Industrial & Engineering Chemistry Research, 2010, 49(19): 9026-9037. |
| [20] |
DIXON A G. Correlations for wall and particle shape effects on fixed bed bulk voidage[J]. The Canadian Journal of Chemical Engineering, 1988, 66(5): 705-718. DOI:10.1002/cjce.5450660501 |
| [21] |
KLERK A D. Voidage variation in packed beds at small column to particle diameter ratio[J]. AIChE Journal, 2003, 49(8): 2022-2029. DOI:10.1002/aic.690490812 |
| [22] |
MUELLER G E. Radial void fraction distributions in randomly packed fixed beds of uniformly sized spheres in cylindrical containers[J]. Powder Technology, 1992, 72(3): 269-275. DOI:10.1016/0032-5910(92)80045-X |
| [23] |
KUVSHINOV G G, MOGILNYKH Y I, KUVSHINOV D G, et al. Peculiarities of filamentous carbon formation in methane decomposition on Ni-containing catalysts[J]. Carbon, 1998, 36(1/2): 87-97. |




