2. 中国船舶集团有限公司第七一八研究所, 河北 邯郸 056027;
3. 清华大学 核能与新能源技术研究院, 北京 100084
2. The 718 Research Institute of CSSC, Handan 056027, China;
3. Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing 100084, China
在未来社会对高效、清洁、安全的能源体系的追求下,质子交换膜燃料电池(PEMFC)成为当今备受关注的绿色电源系统。在PEMFC系统中,常利用引射器或氢气循环泵对电堆出口的氢气引射回流,在提高氢气利用率的同时保持电堆性能。其中,氢气引射器具有体积小、无寄生功率损耗、无噪声等特点,是实现大功率PEMFC氢气循环的主流方向。然而,对于传统的单喷嘴引射器而言,在引射器结构固定后,难以满足燃料电池系统的全功率强变载的需求。
近年来,国内外学者开展了旨在提升引射器性能的结构参数与仿真优化研究。Zhu等[1]提出了一种用于分析引射器流动特性的速度函数,利用计算流体力学(CFD)结合数据回归和参数辨识方法,确定速度函数的指数,并研究了不同电流下氢气子系统的再循环性能。Maghsoodi等[2]讨论了引射器结构对燃料电池系统性能的影响,并利用神经网络和遗传算法寻优。Yin等[3]建立引射器三维数值模型,研究二次流操作条件对引射器性能的影响,结果表明,二次流的湿度大、温度高会降低二次流中的氢气含量。Kou等[4]建立了80 kW PEMFC系统的Matlab/Simulink模型,研究操作条件和几何结构对引射器性能的影响,但文中所建立的燃料电池模型未考虑水汽的影响。为扩大引射器在燃料电池系统中的适用功率范围,一些学者提出不同的引射器结构设计与氢气子系统设计优化。Le Tri等[5]将引射器的一维模型与车用PEMFC集成,研究发现相较于单引射器狭窄的工作范围,双引射器可以实现燃料电池工作范围的全覆盖。Brunner等[6]提出一种可变流量引射器,在一次流喷嘴处设置一针阀,改变喷嘴的开口大小,该引射器在Ballard Mark 9 SSL电堆中性能表现优异。Xue等[7]提出一种多喷嘴喷射器设计思路,通过实验和CFD仿真,认为该设计可以满足燃料电池宽范围的功率输出,同时实现相对稳定的阳极入口压力。Jenssen等[8]在Brunner可变流量引射器的基础上,采用多级串联燃料电池堆设计,提升引射器低功率下的性能。Chen等[9]提出了一种嵌套式引射器,并设置一条与引射器平行的旁路以进一步扩大其工作范围,该引射器的引射性能可以满足150 kW的燃料电池堆在9%~100% 输出功率范围内的供氢需求。目前对于引射器阳极氢气回收性能的研究主要集中在利用计算流体力学软件对其结构参数进行仿真优化,或将实物在所搭建的引射器测试台架中进行气体流动实验。虽然CFD方法有助于深入了解引射器内部的流动行为,但其模型仅简单地模拟了阳极的特性,没有考虑动态响应过程中电堆膜间发生的氢氮渗透与水生成等因素对氢气循环过程及引射特性的影响。
文中利用gFUELCELL仿真建模平台,研究了不同喷嘴开关策略下四喷嘴引射器的引射能力,得到最优喷嘴控制策略,分析该策略下电堆内部物理场变化特性。研究得到燃料电池系统全运行功率下,多喷嘴引射器的最优控制策略,实现了搭载四喷嘴引射器的150 kW流量从5%~100% 的近似线性调控,解决了燃料电池系统低功率区间引射器失效的问题。研究结果为多喷嘴引射器在燃料电池系统中的应用与选型提供了有价值的参考。
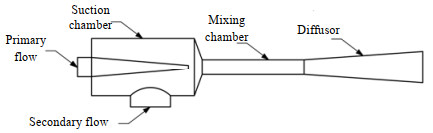
2 四喷嘴引射器氢气子系统 2.1 引射器工作原理引射器是一种进行质量、能量交换的机械装置,其结构由一次进流喷嘴、二次回流管、吸入腔、混合管和扩散管组成。传统单喷嘴氢气引射器结构如图 1所示。在燃料电池系统工作过程中,高压氢气经减压阀调节后,进入一次进流喷嘴。在通过一次进流喷嘴收敛处,气体流速增大,压力减小,在吸入腔内形成一个低压区域。当二次流体回流进口压力高于吸入腔压力时,二次流体会在压差作用下被吸入引射器中,与一次进流一并流入混合管内混合。混合后的流体在扩散管内速度逐渐降低,得到一股满足燃料电池工作压力要求的引射流体。
|
图 1 氢气引射器结构图 Fig.1 Schematic diagram of hydrogen ejector structure |
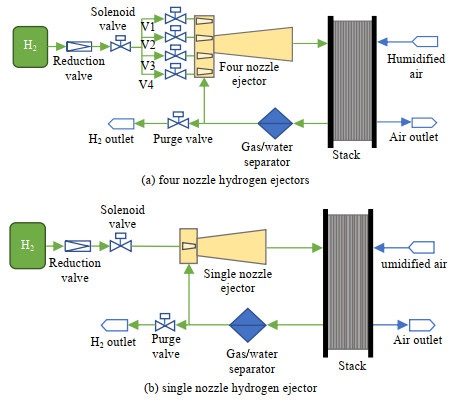
燃料电池氢气循环子系统如图 2所示,四喷嘴氢气引射器的控制技术路线与单喷嘴引射器基本相同,主要由压力调节阀、引射器、燃料电池堆、气水分离器和排氢阀组成。从氢罐供应的氢气经过减压阀和压力调节阀,随后进入氢气引射器,在引射器中一次流氢气与二次回流氢气发生混合,进入燃料电池阳极入口。阳极出口的回流氢气需经过气水分离器,尽可能消除液态水对引射器与阳极入口氢气的影响。四喷嘴氢气引射器通过设计4个不同直径的一次进流喷嘴,调节一次进流喷嘴处电磁阀门V1-V4的开闭,实现不同的引射效果。
|
图 2 燃料电池氢气循环子系统 Fig.2 Schematic diagram of hydrogen recycle subsystems of fuel cells |
本工作基于150 kW燃料电池电堆对引射器进行结构设计,电堆的基本参数如表 1所示。
|
|
表 1 燃料电池工作参数 Table 1 Operation parameters of the fuel cell |
单喷嘴引射器的初始结构设计采用索科洛夫引射器的设计方法[10],对于大功率燃料电池,3~5喷嘴是目前研究者采用较多的选择。为降低喷嘴复杂度,同时实现引射器出口流量的近线性调控,经过前期初步研究,结合实际制造工艺,本工作选择最主流的四喷嘴引射器开展研究。四喷嘴引射器的喉部喷嘴直径按其面积比1:2:4:8将单喷嘴引射器的直径进行分割,引射器的主要结构参数如表 2所示。
|
|
表 2 引射器结构参数 Table 2 Structural parameters of the ejector |
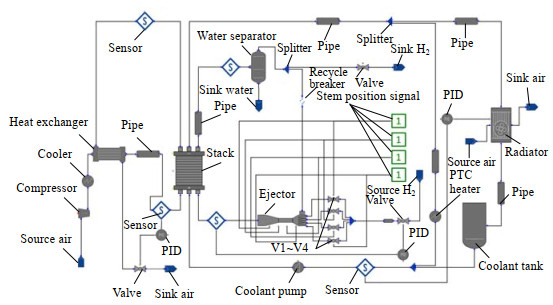
基于图 2(a),利用燃料电池系统仿真软件gFUELCELL平台建立了PEMFC系统模型。模型中包含了电堆模型、氢气子系统模型、空气子系统模型以及冷却子系统模型。在引射器的4个喷嘴前端均设置了电磁阀。通过对4个电磁阀开关的控制,完成各个喷嘴的开闭操作,实现引射器喷嘴工作模式的变化,以适应电堆加载过程中的工作需求。图 3为四喷嘴引射器模型的燃料电池系统模型流程图。
|
图 3 包含四喷嘴引射器模型的燃料电池系统模型 Fig.3 Schematic diagram of the fuel cell system model with a four nozzle ejector |
引射器分为4个区域:(1) 喷嘴区域;(2) 引射区域;(3) 混合段区域和(4) 扩散区域。同时,对引射器模型做出了假设:(1) 模型遵循理想气体状态方程;(2) 进入引射器的水均为气态水;(3) 不考虑径向上的温度和压力变化;(4) 引射器整体绝热。计算时,对部分影响因素进行简化,相关公式采用一定的经验公式进行描述[1]。
3.1 喷嘴段区域计算方程在喷嘴模型中,采用减缩式喷嘴,根据压力比
| $ {p_{{\rm{R, C}}}} = {\left( {\frac{2}{{k + 1}}} \right)^{\frac{k}{{k - 1}}}} $ | (1) |
当流体为亚音速流动时,喷嘴入口的质量流量和喷嘴喉部马赫数计算如下:
| $ {q_{{\rm{m}}, i}}^{{\rm{in}}} = {p^{{\rm{in}}}}{\mathsf{π}}{\left( {\frac{{{D_{{\rm{nozzle}}, i}}}}{2}} \right)^2}\sqrt {\frac{{1.8k\left[ {{{\left( {\frac{{{p_ {\rm{s}}}}}{{{p_ {\rm{p}}}}}} \right)}^{\frac{2}{k}}} - {{\left( {\frac{{{p_ {\rm{s}}}}}{{{p_ {\rm{p}}}}}} \right)}^{\frac{{k + 1}}{k}}}} \right]}}{{\left( {k - 1} \right)\frac{R}{{{M_ {\rm{r}}}_{, {\rm{p}}}}}{T_ {\rm{p}}}}}} $ | (2) |
| $ Ma_{{\rm{nozzle}}, i}^{} = \sqrt {\frac{{2\left[ {1 - {{\left( {\frac{{{p_{\rm{s}}}}}{{{p_{\rm{p}}}}}} \right)}^{\frac{{k - 1}}{k}}}} \right]}}{{\left( {k - 1} \right)}}} $ | (3) |
离开喷嘴喉部的一次流流体,会在吸入室内发生膨胀,该膨胀的极限压力等于二次流压力。通过等熵过程进行计算离开喷嘴后射流体的马赫数、温度、速度和射流流体离开喷嘴后的直径。
| $ M{a_{{\rm{jet}}}} = \sqrt {\frac{{\left[ {{{\left( {\frac{{{p_ {\rm{p}}}}}{{{p_ {\rm{s}}}}}} \right)}^{\frac{{k - 1}}{k}}} - 1} \right]}}{{0.5\left( {k - 1} \right)}}} $ | (4) |
| $ \frac{T_{\mathrm{p}}}{T_{\mathrm{jet}}}=1+0.5(k-1) M a_{\mathrm{jet}}^2 $ | (5) |
| $ {v_{{\rm{jet}}}} = M{a_{{\rm{jet}}}}{\left( {k\frac{R}{{{M_{{\rm{r,p}}}}}}{T_{{\rm{jet}}}}} \right)^{0.5}} $ | (6) |
| $ \sqrt {0.9} \frac{{{D_{{\rm{jet}}}}}}{{D_{{\rm{nozzle}}, i}^{}}} = {\left( {\frac{{Ma_{{\rm{nozzle}}, i}^{}}}{{M{a_{{\rm{jet}}}}}}} \right)^{0.5}}{\left[ {\frac{{2 + \left( {k + 1} \right)Ma_{{\rm{jet}}}^2}}{{2 + \left( {k + 1} \right)Ma{{_{{\rm{nozzle}}, i}^{}}^2}}}} \right]^{\frac{{k + 1}}{{4\left( {k - 1} \right)}}}} $ | (7) |
进入混合段之前,引射流体质量流量、速度、马赫数和温度计算如下:
| $ {q_{m, {\rm{s}}}} = \frac{{{\mathsf{π}}{\rho _ {\rm{s}}}{v_{{\rm{jet}}}}\left( {{D_{{\rm{mix}}}} - {D_{{\rm{jet}}}}} \right)\left[ {{D_{{\rm{mix}}}} + \left( {1 + {n_v}} \right){D_{{\rm{jet}}}}} \right]}}{{2\left( {{n_v} + 1} \right)\left( {{n_v} + 2} \right)}} $ | (8) |
其中,混合段速度分布系数,利用经验方程进行计算:
| $ {n_v} = {0.000\;}{139\;}{3_{}}\;{{\rm{exp}}_{}}\frac{{\left( {\frac{{p_{\rm{s}}^{0.8}}}{{p_ {\rm{p}}^{1.1}}}} \right)}}{{0.05}} + 0.456\left( {\frac{{{D_{{\rm{mix}}}}}}{{{D_{{\rm{nozzle}}}}}}} \right) + {0.166\;}8 $ | (9) |
| $ {v_{{\rm{s}}, 2}} = \frac{{2{v_{{\rm{jet}}}}\left[ {{D_{{\rm{mix}}}} + \left( {1 + {n_v}} \right){D_{{\rm{jet}}}}} \right]}}{{\left( {{n_v} + 1} \right)\left( {{n_v} + 2} \right)\left( {{D_{{\rm{mix}}}} + {D_{{\rm{jet}}}}} \right)}} $ | (10) |
| $ {v_{{\rm{s}}, 2}} = M{a_{{\rm{s}}, 2}}{\left( {k\frac{R}{{{M_{\rm{r, s}}}}}{T_{{\rm{s}}, 2}}} \right)^{0.5}} $ | (11) |
| $ \frac{{{T_{\rm{s}}}}}{{{T_{{\rm{s}}, 2}}}} = 1 + 0.5\left( {k - 1} \right)Ma_{{\rm{s}}, 2}^2 $ | (12) |
射流流体和引射流体进入混合段后发生混合。根据动量守恒方程:
| $ 0.9\left( {{q_{m, {\rm{p}}}}{v_{{\rm{jet}}}} + {q_{m, {\rm{s}}}}{v_{{\rm{s}}, 2}}} \right) = \left( {{q_{m, {\rm{p}}}} + {q_{m, {\rm{s}}}}} \right){v_{{\rm{mix}}}} $ | (13) |
混合段的能量守恒方程如下:
| $ {q_{m, {\rm{p}}}}\left( {{h_{{\rm{jet}}}} + \frac{{v_{{\rm{jet}}}^2}}{2}} \right) + {q_{m,{\rm{s}}}}\left( {{h_{{\rm{s}}, 2}} + \frac{{v_{{\rm{s}}, 2}^2}}{2}} \right) = \left( {{q_{m, {\rm{p}}}} + {q_{m, {\rm{s}}}}} \right)\left( {{h_{{\rm{mix}}}} + \frac{{v_{{\rm{mix}}}^2}}{2}} \right) $ | (14) |
其中,混合段的混合流体速度
| $ {v_{{\rm{mix}}}} = M{a_{{\rm{mix}}}}{\left( {k\frac{R}{{{M_{{\rm{r}},{{\rm{mix}}}}}}}{T_{{\rm{mix}}}}} \right)^{0.5}} $ | (15) |
扩散段的作用主要是增大流通截面积、提升引射器出口压力。在扩散段中,由等熵过程相关方程得出出口压力,其计算式为:
| $ \frac{{{p_{{\rm{out}}}}}}{{{p_{{\rm{mix}}}}}} = {\left[ {1 + 0.5\left( {k - 1} \right)Ma_{{\rm{mix}}}^2} \right]^{\frac{k}{{k - 1}}}} $ | (16) |
对于引射器本身,其能量守恒方程如下:
| $ {q_{m, {\rm{p}}}}{h_{\rm{p}}} + {q_{m, {\rm{s}}}}{h_ {\rm{s}}} = \left( {{q_{m, {\rm{p}}}} + {q_{m,{\rm{s}}}}} \right){h_{{\rm{out}}}} $ | (17) |
为了评价引射器的性能,引入引射比、氢气化学计量比2个重要参数:
| $ \mu = \frac{{{q_{m, {\rm{s}}}}}}{{{q_{m, {\rm{p}}}}}} $ | (18) |
| $ {S_{{{\rm{H}}_2}}} = \frac{{2F\left( {{q_{m, {\rm{p}}}}{w_{{\rm{p}},{{\rm{H}}_2}}} + {q_{m, {\rm{s}}}}{w_{{\rm{s}}, {{\rm{H}}_2}}}} \right)}}{{I{M_{{{\rm{H}}_2}}}}} $ | (19) |
根据4个喷嘴的阀门开关策略不同,共有15种控制模式,根据喷嘴段一次流量公式,可以看出一次质量流量与喷嘴喉部面积呈正比。因此对于四喷嘴引射器,以四喷嘴全开的最大供氢流量占比为100%来计算,可以得到每种控制模式下的最大供氢流量占比。每个控制模式下的喷嘴开关策略及供氢流量占比如表 3所示。
|
|
表 3 四喷嘴引射器控制模式表 Table 3 Control modes of the four nozzle ejector |
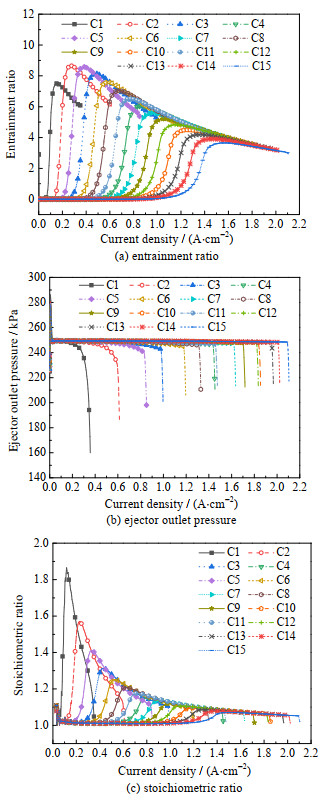
从图 4(a)可以看出,单一喷嘴模式下引射器能起到引射能力的工作区间有一定的局限性,其引射比在工作区间内呈先上升后下降的趋势。在相对较低的电流密度下,引射比几乎为0,这是因为当运行电流密度相对较小时,阳极侧氢气消耗量也较小,氢气源出口的压力调节阀会通过减小阀门开度,降低引射器一次流进口压力,从而保持电堆阳极进口处氢气压力的稳定,与此同时,过低的一次流进口压力导致射流流体速度降低,在吸入室产生的负压较小,最终导致在低功率情况下,引射器失效。在其工作区间内,随着电堆电流密度的增大,阳极侧氢气消耗量随之上升,氢气出口压力调节阀逐渐增大阀门开度,一次流质量流量与压力不断增加,此时吸入室产生的负压不断增大,引射比不断上升到达峰值。
|
图 4 不同控制模式对引射性能的影响 Fig.4 Effects of different control modes on ejector performance |
图 4(b)为不同控制模式下阳极侧进堆氢气压力随电流密度变化的曲线,对于单一喷嘴控制模式而言,当电流密度进一步增大,氢气需求量逐渐到达该引射器控制模式的上限,导致其无法维持电堆所需的氢气流量及压力,引射性能逐渐下降。分析原因是,当喷嘴直径变小,其内部流阻变大,若要引射同样流量的气体,需要更高的射流入口压力,而射流入口压力取决于比例阀特性以及其氢气前端压力值。因此,当系统中比例阀特性与前端压力值一定时,就必然决定了固定结构式引射器在小喷嘴直径下无法满足高功率的需求。
对比图 4(a)与(c),可以看出在单一喷嘴模式下,氢气计量比和引射比的变化趋势基本相同。引射比增加,更多的氢气通过引射器再循环到阳极,氢气计量比随之增加。
4.2 四喷嘴引射器在大功率PEMFC系统控制策略单一喷嘴模式的工作范围有限,虽然小喷嘴直径模式可以满足低电流运行的要求,但在高电流区间会失效。而大喷嘴直径模式则相反,其在低电流区间几乎不能产生引射。因此,根据上述特性,结合15种控制模式下的进堆压力值与氢气计量比变化趋势,得到四喷嘴引射器在燃料电池堆全功率区间变流量稳压供氢控制策略,如表 4所示。
|
|
表 4 不同电流区间对应的四喷嘴引射器控制策略 Table 4 Control Strategies for the four nozzle ejectors at different current ranges |
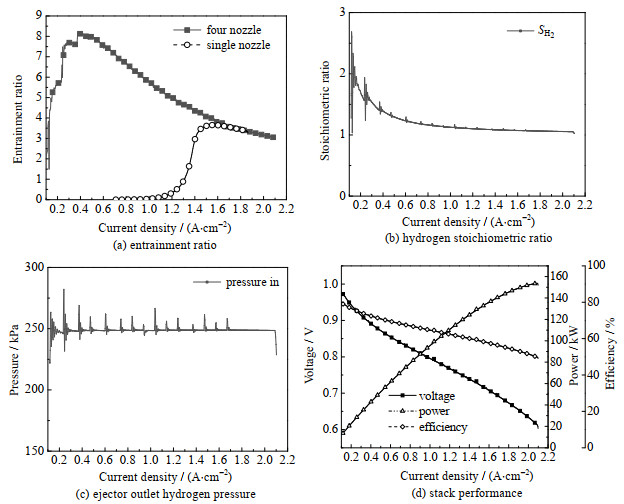
根据表 4,对全功率区间多喷嘴引射器系统控制进行仿真。从图 5(a)可以看到,在对四喷嘴引射器进行控制策略优化后,可以实现0.11~2.11 A⋅cm−2电流密度范围内的引射,与单喷嘴引射器1.30~1.86 A⋅cm−2的作用区间相比,其运行工况覆盖范围扩大至5%~100%。
|
图 5 四喷嘴引射器控制策略下的性能变化曲线 Fig.5 Performance profiles under the control strategy of four nozzle ejector |
图 5(b)为优化控制策略下电流拉载过程中氢气计量比变化曲线,可以看到随着拉载电流的增加,氢气计量比逐渐下降,在电流密度为0.1~0.5 A⋅cm−2时下降较快,分析原因是在该区间内引射比呈上升趋势,增加的引射比意味着更多的二次回流氢气,而随着拉载电流的增大,阳极的氮气含量累积量也在快速增加,从而导致经引射器送入阳极的氢气中氮气含量增加,氢气计量比快速下降。其中,阳极侧氮气的产生是由于质子交换膜间发生了气体渗透现象。原理上,质子交换膜中反应气体是不会发生渗透的,防止反应物组分在电化学反应发生前混合。然而,由于膜的多孔结构,水含量以及氢和氧在水中的可溶解性等原因,PEM之间会发生微量气体渗透过程。图 5(c)为优化控制策略下电流拉载过程中阳极入口氢气压力变化曲线,可以看到在电流拉载的过程中,阳极入口压力控制在250 kPa的目标值,其中压力的较大波动是由喷嘴控制模式切换导致,小幅波动受排氢阀间歇排氢的影响。图 5(b)为优化策略下电流拉载过程中电堆性能曲线,可以看到随着电流密度的增加,电堆效率与单片电压逐渐降低,电堆功率逐渐上升。
图 6是电流拉载时,阴极/阳极氮气累积量与氮气摩尔通量变化曲线。在电流密度小于1.0 A⋅cm−2,PEM氮气摩尔通量为负值,氮气从阴极向阳极扩散,在阴极入口流量及排氢策略不变的情况下,阴极氮气含量不断下降,阳极氮气含量不断上升逐渐大于阴极,当电流密度大于1.0 A⋅cm−2时,PEM氮气摩尔通量为正值,氮气开始从阳极向阴极扩散。

|
图 6 电流拉载过程中,阴极/阳极氮气累积量与PEM氮气摩尔通量变化曲线 Fig.6 Cathode/anode nitrogen molar accumulation as a function of PEM nitrogen molar flux diffusion during the current pulling process |
图 7为电流拉载过程中,引射器出口压力变化对引射性能的影响。可以看到,引射器出口气体压力变化对喷嘴模式切换波动几乎无影响,随着引射器出口压力的增大,引射比、氢气计量比和出口质量流量均增大,且输出电流越大,引射器出口压力对出口质量流量的影响越明显。

|
图 7 引射器出口压力变化对引射性能的影响 Fig.7 Effects of outlet pressure variation on ejector performance |
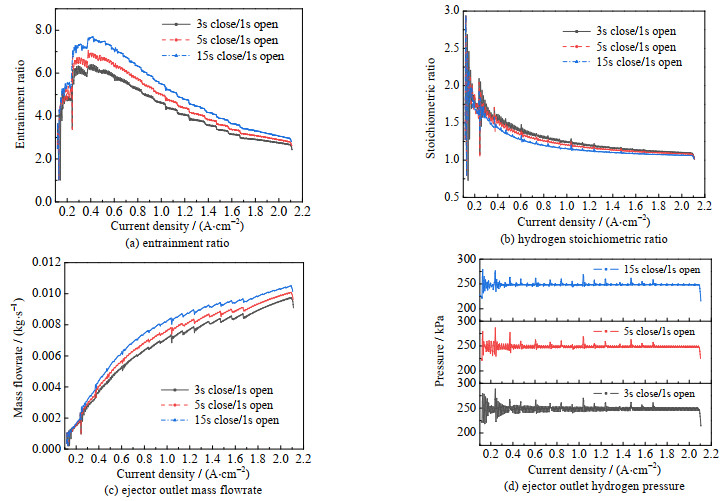
图 8为排氢频率对引射性能的影响,可以看到,减小排氢频率可以提升引射器引射比和出口质量流量,但同时增加了氢气回路内的氮气累积量,氢气计量比降低。而增大排氢频率会使喷嘴模式切换带来的出口质量流量波动更加明显,出口压力波动也较为剧烈。因此,在实际系统运行过程中,需要针对不同电流工况设置合适的排氢频率。
|
图 8 氢气路尾排频率对引射性能的影响 Fig.8 Effects of exhaust frequency on the eject performance |
对四喷嘴氢气引射器在大功率PEMFC氢气子系统的性能开展建模与研究,采用集总参数建模方法对四喷嘴引射器进行建模,研究了四喷嘴引射器控制模式对引射比的影响,同时优化喷嘴控制策略,进行全功率区间氢气子系统仿真,得到以下结论:
(1) 每一种喷嘴控制模式下,引射器具有引射能力时,电堆的运行电流区间有一定的局限性,在引射作用区间,随着电堆运行电流的增加,其引射比先升高后下降,存在一个最大值。
(2) 混合段直径不变,随着喷嘴喉部面积减小,引射器的作用区间逐渐向低电流工况移动,同时整体的引射比升高,在作用区间内的引射性能变化也更加剧烈。
(3) 提出了四喷嘴引射器在不同电流区间的阀门控制策略,使其能够满足功率为8~153 kW的电堆稳压供氢需求。
(4) 引射器出口压力增大,引射比和出口质量流量均增大,引射性能提升。
符号说明:
D ⎯ 直径,mm
w ⎯ 质量分数,% F ⎯ 法拉第常数,C⋅mol−1
μ ⎯ 引射比/引射系数 h ⎯ 比焓,J⋅kg−1,h=CpT(Cp为比定压热容)
ρ ⎯ 密度,kg⋅m−3 I ⎯ 电流,A
上标 in ⎯ 引射器喷嘴进口 M ⎯ 摩尔质量,kg⋅mol−1
out ⎯ 引射器出口 Mr ⎯ 相对分子质量,kg⋅mol−1
下标 Ma ⎯ 马赫数
i ⎯ 喷嘴数量 nv ⎯ 混合段速度分布系数
jet ⎯ 离开喷嘴后的射流流体 p ⎯ 压力,kPa
mix ⎯ 混合段 qm ⎯ 质量流量,kg⋅s−1
nozzle ⎯ 喷嘴喉部 R ⎯ 摩尔气体常数,J⋅mol−1⋅K−1
p ⎯ 一次流流体/射流流体 S ⎯ 化学计量比
R, C ⎯ 临界比值 T ⎯ 温度,K
s ⎯ 二次流流体/引射流体 v ⎯ 速度,m⋅s−1
s, 2 ⎯ 进入混合段的引射流体
| [1] |
ZHU Y H, LI Y Z. New theoretical model for convergent nozzle ejector in the proton exchange membrane fuel cell system[J]. Journal of Power Sources, 2009, 191(2): 510-519. DOI:10.1016/j.jpowsour.2009.02.014 |
| [2] |
MAGHSOODI A, AFSHARI E, AHMADIKIA H. Optimization of geometric parameters for design a high-performance ejector in the proton exchange membrane fuel cell system using artificial neural network and genetic algorithm[J]. Applied Thermal Engineering, 2014, 71(1): 410-418. DOI:10.1016/j.applthermaleng.2014.06.067 |
| [3] |
YIN Y, FAN M Z, JIAO K, et al. Numerical investigation of an ejector for anode recirculation in proton exchange membrane fuel cell system[J]. Energy Conversion and Management, 2016, 126: 1106-1117. DOI:10.1016/j.enconman.2016.09.024 |
| [4] |
KUO J K, HSIEH C Y. Numerical investigation into effects of ejector geometry and operating conditions on hydrogen recirculation ratio in 80 kW PEM fuel cell system[J]. Energy, 2021, 233: 121100. DOI:10.1016/j.energy.2021.121100 |
| [5] |
LE TRI D T, VU H N, NGUYEN H L, et al. A comparative study of single and dual ejector concepts for anodic recirculation system in high-performance vehicular proton exchange membrane fuel cells[J]. International Journal of Hydrogen Energy, 2023, 48(70): 27334-27360. |
| [6] |
BRUNNER D A, MARCKS S, BAJPAI M, et al. Design and characterization of an electronically controlled variable flow rate ejector for fuel cell applications[J]. International Journal of Hydrogen Energy, 2012, 37(5): 4457-4466. DOI:10.1016/j.ijhydene.2011.11.116 |
| [7] |
XUE H Y, WANG L, ZHANG H L, et al. Design and investigation of multi-nozzle ejector for PEMFC hydrogen recirculation[J]. International Journal of Hydrogen Energy, 2020, 45(28): 14500-14516. DOI:10.1016/j.ijhydene.2020.03.166 |
| [8] |
JENSSEN D, BERGER O, KREWER U. Improved PEM fuel cell system operation with cascaded stack and ejector-based recirculation[J]. Applied Energy, 2017, 195: 324-333. DOI:10.1016/j.apenergy.2017.03.002 |
| [9] |
CHEN L, XU K D, YANG Z Y, et al. Optimal design of a novel nested-nozzle ejector for PEMFC's hydrogen supply and recirculation system[J]. International Journal of Hydrogen Energy, 2023, 48(70): 27330-27343. DOI:10.1016/j.ijhydene.2023.03.403 |
| [10] |
索科洛夫E Я, 津格尔H M. 喷射器[M]. 黄秋云, 译. 北京: 科学出版社, 1977. SOKOLOV E Я, ZINGEL H M. Ejector [M]. HUANG Q Y, trans. Beijing: Science Press, 1977. |




