2. 辽宁石油化工大学 石油化工学院, 辽宁 抚顺 113001;
3. 辽宁石油化工大学环境与安全工程学院, 辽宁 抚顺 113001
2. College of Petrochemical Engineering, Liaoning Petrochemical University, Fushun 113001, China;
3. College of Chemical Engineering and Environmental Engineering, Liaoning Petrochemical University, Fushun 113001, China
为满足人们日益增长的需求,化石燃料用量日益增加。由中国能源网统计数据可知,我国工业余热资源占化石燃料消耗总量的17%~67%,其中60% 的余热资源都可以再次被回收利用[1]。因此,作为能够缓解能源和环境问题的有效对策,余热利用越来越受重视。天然气作为一种具有高热值的清洁能源,被广泛用于能源工业[2]。天然气的成分中不含硫,因此在燃烧过程中不会产生二氧化硫等污染环境的气体,并且产生二氧化碳的量也远低于石油和煤炭。天然气在大约-162 ℃的温度和常压下被液化,以便于运输和存储[3]。因此,将液化天然气(LNG)输送到终端之前应进行气化,LNG气化过程将释放约830 kJ·kg-1的冷量[4]。如果能将这部分冷能与天然气燃烧后产生的余热联合利用,并对余热中的二氧化碳进行捕集,将可以有效地改善我国的能源消费结构,提高能源的综合利用效率,同时对环境保护也起到一定作用。
目前,国内外学者对余热与LNG冷能的利用进行研究。潘振等[5]以朗肯循环为基础设计一种利用低温燃煤废气和LNG冷能的三级式利用系统。与二级式系统对比后发现,三级式系统的热效率和㶲效率分别提高了57.74% 和36.67%。张丽等[6]设计了一种对水平井蒸汽辅助泄油(SAGD)稠油开采余热进行吸收利用的冷热电三联供系统,并产生了每年约270万元的经济效益。梁莹等[7]为梯级利用LNG冷能和烟气余热设计了一套布雷顿(Brayton)循环和有机朗肯循环(ORC)结合的发电系统,经模拟计算后得知,该发电系统净发电效率比常规的燃气-蒸气联合循环发电系统效率提高了11.16%。Sun等[8]对LNG直接膨胀分别与单级ORC、并联两级ORC和级联两级ORC联合的系统进行分析比较,计算结果表明在热源温度较低时,并联两级ORC表现更佳,而级联两级ORC更适用于较高温度热源。
目前针对余热与LNG冷能利用的研究大多以单级ORC与Brayton循环为主,LNG冷能没有得到充分的利用。因此,本文提出一种氮气回热Brayton与乙烯-丙烷二级ORC联合的动力循环。该循环以烟气为热源,以LNG为冷源。其中,氮气回热Brayton循环利用低温部分的LNG冷量,而乙烯-丙烷二级ORC回收高温部分的LNG冷量[9],进而实现能量的梯级利用。分析蒸发温度、蒸发压力等热力学参数对循环性能的影响,并对系统进行技术经济学分析,使能量得到更为合理的利用。
2 系统简介与模型建立 2.1 系统介绍利用中低温余热的LNG冷能发电方式主要有:直接膨胀法、联合ORC法以及氮气Brayton法[9]。但该方法不能充分高效地利用LNG的冷量,造成了能量的浪费。为使LNG的冷量得到充分的利用,本文提出了一种氮气回热Brayton与乙烯-丙烷二级ORC联合的动力循环。该循环以LNG作为冷源,热源为天然气在纯氧中完全燃烧后得到的烟气。其中,烟气为CO2和水蒸气的混合气体,CO2和水蒸气的量比n(CO2): n(H2O)=1:2。系统模拟主要参数如表 1所示。具体流程设计如图 1所示。
|
|
表 1 系统模拟主要参数 Table 1 Simulation parameters of the system |
|
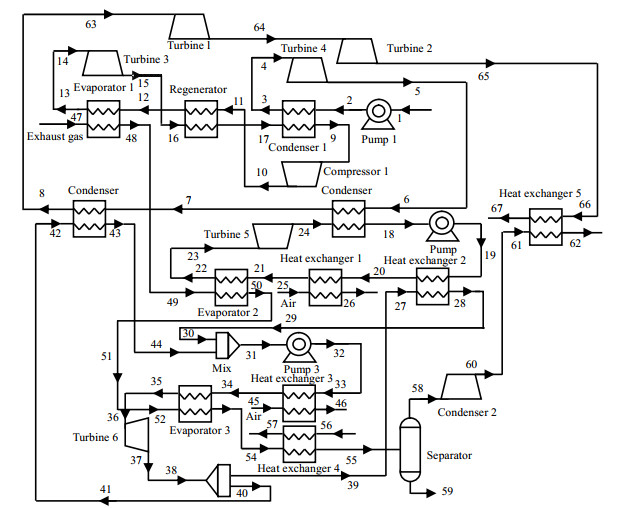
图 1 氮气回热Brayton与乙烯-丙烷二级ORC联合动力循环系统流程图 Fig.1 Flow chart of the combined power cycle system with nitrogen regenerative Brayton cycle and ethylene-propane secondary ORC |
LNG经过泵1加压后进入冷凝器1中,升温后进入透平机4膨胀对外做功,接着依次进入冷凝器2、3中,为乙烯-丙烷二级ORC提供冷量。而被LNG冷凝为液体的乙烯进入换热器2向丙烷提供冷量。而利用乙烯和LNG冷量的丙烷汇聚一起经泵3加压后,进入透平机5膨胀做功。烟气依次与氮气、乙烯、丙烷、循环水进行换热后,温度降到常温后进入分离器。经过气液分离后,CO2经过压缩机2升压后进入换热器5中,在其中被连续升温并膨胀做功后的LNG冷却液化,从而完成碳捕集。
2.2 假设条件本文通过使用数值模拟软件对系统性能进行模拟计算。根据给定的烟气质量流量,选用P-R方程对循环进行模拟计算。为简化计算,对本文模型进行如下假设:LNG由纯甲烷组成[10];忽略换热器和管道中的压降损失[11-12],系统内流体处于稳定流动状[13];泵、透平机以及压缩机效率均为给定值75%。
2.3 热力学模型烟气进入蒸发器1所释放的热量为
| $ \mathop Q\nolimits_{{\rm{in}}} = {q_{m{\rm{, h}}}}\left( {\mathop h\nolimits_{{\rm{in}}} - \mathop h\nolimits_{{\rm{out}}} } \right) $ | (1) |
式中:qm, h为烟气质量流量,单位:kg·h-1;hin和hout分别为烟气进出口的比焓,单位:kJ·kg-1。
冷水所提供的能量为
| $ \mathop Q\nolimits_{{{\rm{H}}_{\rm{2}}}{\rm{O}}} {\rm{ = }}{q_{m{\rm{, 56}}}}\left( {\mathop h\nolimits_{{\rm{56}}} - \mathop h\nolimits_{{\rm{57}}} } \right) $ | (2) |
式中:qm, 56为流程节点56质量流量,单位:kg·h-1;h56和h57分别为流程节点56和57的比焓,单位:kJ·kg-1。
热空气所提供的热量为
| $ \mathop Q\nolimits_{{\rm{air}}} = {q_{m{\rm{, 26}}}}\left( {\mathop h\nolimits_{26} - \mathop h\nolimits_{25} } \right) + {q_{m{\rm{, 46}}}}\left( {\mathop h\nolimits_{46} - \mathop h\nolimits_{45} } \right) $ | (3) |
式中:qm, 26和qm, 46分别为流程节点26和46质量流量,单位:kg·h-1;h25、h26、h45和h46分别为流程节点25、26、45和46的比焓,单位:kJ·kg-1。
系统净输出功为
| $ \mathop W\nolimits_{{\rm{net}}} = \sum {\mathop W\nolimits_{{\rm{tur}}} } - \sum {\mathop W\nolimits_{{\rm{pump}}} } - \sum {\mathop W\nolimits_{{\rm{com}}} } $ | (4) |
式中:Wtur为透平机所做的功,单位:kW;Wpump和Wcom分别为泵和压缩机所消耗的功,单位:kW。
系统热效率为
| $ \mathop \eta \nolimits_{{\rm{th}}} = \frac{{\mathop W\nolimits_{{\rm{net}}} }}{{\mathop Q\nolimits_{{\rm{in}}} }} $ | (5) |
各流体的㶲值为
| $ {E_i}\mathop { = q}\nolimits_{m, i} \left[ {\left( {\mathop h\nolimits_i - \mathop h\nolimits_0 } \right) - {T_0}\left( {\mathop s\nolimits_i - \mathop s\nolimits_0 } \right)} \right] $ | (6) |
式中:qm, i为各流体的质量流量,单位:kg·h-1;h0、s0为标准状态下(温度为298.15 K,压力为101.325 kPa)流体的比焓和比熵,单位:kJ·kg-1和kJ·(kg·K)-1;hi、si分别为流体的比焓和比熵,单位:kJ·kg-1和kJ·(kg·K)-1;T0为标准状态的温度,取值为298.15 K。
各设备㶲损为
| $ {I_i} = \mathop E\nolimits_{{\rm{xiao}}} - \mathop E\nolimits_{{\rm{shou}}} $ | (7) |
式中:Exiao和Eshou分别为循环中的消耗㶲和收益㶲,单位:kW。
各设备㶲损率为
| $ \mathop \eta \nolimits_{{\rm{ex - }}i} = \frac{{\mathop I\nolimits_i }}{{\mathop I\nolimits_{{\rm{tot}}} }} $ | (8) |
式中:Ii和Itot分别为各设备㶲损和总㶲损,单位:kW。
各设备㶲损失系数为
| $ \mathop \xi \nolimits_i = \frac{{\mathop I\nolimits_i }}{{\mathop E\nolimits_{{\rm{xiao}}} }} $ | (9) |
系统㶲效率为
| $ \mathop \eta \nolimits_{{\rm{ex}}} = \frac{{\mathop E\nolimits_{{\rm{out}}} }}{{\mathop E\nolimits_{{\rm{in}}} }} $ | (10) |
式中:Ein和Eout分别为循环中各设备的进口㶲和出口㶲,单位:kW。
2.4 经济模型循环各设备的投资成本如式(11)~(20)[14-16]所示。式中:K1、K2、K3、M1、M2、M3、B1、B2、Fm和Fbm为常数,取值见表 2。
热交换器投资成本为
| $ \mathop C\nolimits_{{\rm{bm, heat}}} = \mathop C\nolimits_{{\rm{p, heat}}} \times \left( {\mathop B\nolimits_{{\rm{1, heat}}} + \mathop B\nolimits_{{\rm{2, heat}}} \times \mathop F\nolimits_{{\rm{m, heat}}} \times \mathop F\nolimits_{{\rm{p, heat}}} } \right) $ | (11) |
| $ \mathop {\lg C}\nolimits_{{\rm{p, heat}}} = \mathop K\nolimits_{{\rm{1, heat}}} + \mathop K\nolimits_{{\rm{2, heat}}} \times \lg \mathop A\nolimits_{{\rm{heat}}} $ | (12) |
| $ \mathop {\lg F}\nolimits_{{\rm{p, heat}}} = \mathop M\nolimits_{{\rm{1, heat}}} + \mathop M\nolimits_{{\rm{2, heat}}} \times \lg \mathop p\nolimits_{{\rm{heat}}} $ | (13) |
式中:Aheat为热交换器的换热面积,单位:m2;pheat为热交换器压力,单位:MPa。
透平机投资成本为
| $ \mathop C\nolimits_{{\rm{bm, tur}}} = \mathop C\nolimits_{{\rm{p, tur}}} \times \mathop F\nolimits_{{\rm{bm, tur}}} $ | (14) |
| $ \mathop {\lg C}\nolimits_{{\rm{p, tur}}} = \mathop K\nolimits_{{\rm{1, tur}}} + \mathop K\nolimits_{{\rm{2, tur}}} \times \mathop {\lg W}\nolimits_{{\rm{tur}}} $ | (15) |
泵投资成本为
| $ \mathop C\nolimits_{{\rm{bm, pump}}} = \mathop C\nolimits_{{\rm{p, pump}}} \times \left( {\mathop B\nolimits_{{\rm{1, pump}}} + \mathop B\nolimits_{{\rm{2, pump}}} \times \mathop F\nolimits_{{\rm{bm, pump}}} } \right) $ | (16) |
| $ \mathop {\lg C}\nolimits_{{\rm{p, pump}}} = \mathop K\nolimits_{{\rm{1, pump}}} + \mathop K\nolimits_{{\rm{2, pump}}} \times \mathop {\lg W}\nolimits_{{\rm{pump}}} + \mathop K\nolimits_{{\rm{3, pump}}} \times \mathop {\left( {\mathop {\lg W}\nolimits_{{\rm{pump}}} } \right)}\nolimits^2 $ | (17) |
压缩机投资成本为
| $ \mathop C\nolimits_{{\rm{bm, com}}} = \mathop C\nolimits_{{\rm{p, com}}} \times \left( {\mathop B\nolimits_{{\rm{1, com}}} + \mathop B\nolimits_{{\rm{2, com}}} \times \mathop F\nolimits_{{\rm{m, com}}} \times \mathop F\nolimits_{{\rm{p, com}}} } \right) $ | (18) |
| $ \mathop {\lg C}\nolimits_{{\rm{p, com}}} = \mathop K\nolimits_{{\rm{1, com}}} + \mathop K\nolimits_{{\rm{2, com}}} \times \mathop {\lg W}\nolimits_{{\rm{com}}} + \mathop K\nolimits_{{\rm{3, com}}} \times \mathop {\left( {\mathop {\lg W}\nolimits_{{\rm{com}}} } \right)}\nolimits^2 $ | (19) |
| $ \mathop F\nolimits_{{\rm{p, com}}} = \mathop M\nolimits_{{\rm{1, com}}} + \mathop M\nolimits_{{\rm{2, com}}} \times \mathop {\lg p}\nolimits_{{\rm{com}}} + \mathop M\nolimits_{{\rm{3, com}}} \times \mathop {\left( {\mathop {\lg p}\nolimits_{{\rm{com}}} } \right)}\nolimits^2 $ | (20) |
式中:pcom为压缩机压力,单位:MPa。
热交换器换热面积为
| $ \mathop A\nolimits_{{\rm{heat}}} = \frac{{\mathop Q\nolimits_{{\rm{heat}}} }}{{U \times \Delta T}} $ | (21) |
式中:Qheat为热交换器的换热量,单位:kW;U为热交换器的传热系数,单位:W·(m2·K)-1;ΔT为热交换器的对数平均温差,单位:K。
1996年以美元为单位的系统设备的总投资成本[17]为
| $ \mathop C\nolimits_{{\rm{bm1996}}} = \mathop C\nolimits_{{\rm{bm, heat}}} + \mathop C\nolimits_{{\rm{bm, tur}}} + \mathop C\nolimits_{{\rm{bm, pump}}} + \mathop C\nolimits_{{\rm{bm, com}}} $ | (22) |
2020年系统设备的总投资成本为
| $ \mathop C\nolimits_{{\rm{bm2020}}} = \mathop C\nolimits_{{\rm{bm1996}}} \frac{{\mathop {{\rm{CEPCI}}}\nolimits_{{\rm{2020}}} }}{{\mathop {{\rm{CEPCI}}}\nolimits_{{\rm{1996}}} }} $ | (23) |
式中:CEPCI1996和CEPCI2020分别为1996年和2020年的化学经济工厂成本指数,数值分别为382和668[18]。
成本回收系数为
| $ {\rm{CRF}} = \frac{{i\mathop {\left( {1 + i} \right)}\nolimits^{\mathop t\nolimits_{\rm{s}} } }}{{\mathop {\left( {1 + i} \right)}\nolimits^{\mathop t\nolimits_{\rm{s}} } - 1}} $ | (24) |
式中:i为年利率,取值6%;ts为系统正常使用寿命,取值20 a[16]。
当发电量为1 kW·h时的系统成本为
| $ {\rm{LEC}} = \frac{{{\rm{CRF}} \times \mathop C\nolimits_{{\rm{bm2020}}} + {\rm{COMs}}}}{{\mathop W\nolimits_{{\rm{net}}} \times \mathop t\nolimits_{{\rm{run}}} }} $ | (25) |
式中:trun为系统年度运行时间,取值8 600 h;COMs为系统管理和运行成本,其值为设备投资成本的1.5%[16]。
系统的年度净资产为
| $ {\rm{NE}} = \mathop P\nolimits_{\rm{e}} \times \mathop W\nolimits_{{\rm{net}}} \times \mathop t\nolimits_{{\rm{run}}} + \mathop C\nolimits_{\rm{r}} \times \mathop Q\nolimits_{\rm{r}} \times \mathop t\nolimits_{{\rm{run}}} $ | (26) |
式中:Pe为工业用电价格,取值0.1548 $·kW-1·h-1;Cr为热能价格,取值6.8 $·GJ-1;Qr为热量消耗[16],单位:GJ。
系统的折旧回收期为
| $ {\rm{DPP}} = \frac{{\ln \frac{{{\rm{NE}} - COMs}}{{{\rm{NE}} - {\rm{COMs}} - i\mathop C\nolimits_{{\rm{bm2020}}} }}}}{{\ln \left( {1 + i} \right)}} $ | (27) |
将系统分成氮气回热Brayton循环和乙烯-丙烷二级ORC两个部分进行分析。分析氮气质量流量、蒸发温度以及蒸发压力对系统性能的影响。
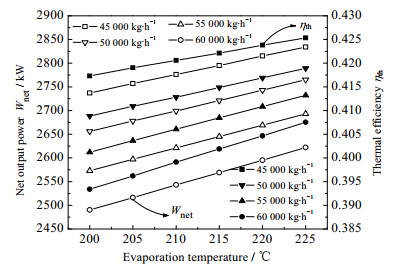
3.1 氮气回热Brayton循环如图 2所示为系统净输出功和热效率在不同氮气质量流量随蒸发温度变化的情况。从图 2中可以看出,系统净输出功和热效率均随着蒸发温度的升高呈现增加的趋势,而随着氮气质量流量的增多呈现减少的趋势。出现上述趋势的原因是,改变透平机进口温度会使其焓差发生变化。透平机的焓降随着温度的升高而增加,从而做功量增多,进而净输出功增多;而当氮气质量流量增多时,虽然透平机3的做功量随之增大,但压缩机1消耗的压缩功大于其做功量,因此由公式(4)可知,净输出功呈现减小的趋势。在蒸发温度升高时,虽然总吸热量也随之增多,但涨幅小于净输出功增长量,因此热效率随蒸发温度的升高而增加;当氮气质量流量增多时,虽然总吸热量随之减小,但净输出功减少量大于其减小幅度,因此热效率的变化趋势与净输出功相似。
|
图 2 系统净输出功和热效率在不同氮气质量流量随蒸发温度的变化 Fig.2 Profiles of net output power and thermal efficiency of the system as a function of nitrogen mass flow rate under different evaporation temperatures |
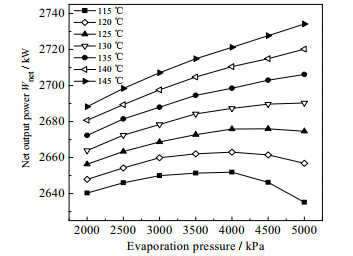
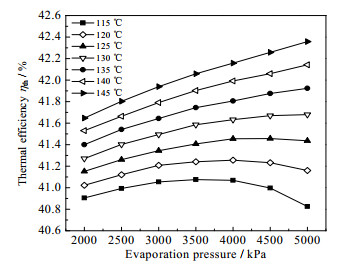
如图 3和4所示分别为系统净输出功和热效率在不同蒸发温度下对蒸发压力的变化情况。由图 3和4可知,系统净输出功和热效率均随着蒸发温度的升高呈线性增加趋势。当蒸发温度小于125 ℃时,蒸发压力的增大使得系统净输出功和热效率均呈现先增大后减小的趋势,最佳蒸发压力为4 000 kPa;当蒸发温度大于125 ℃时,系统净输出功和热效率均随着蒸发压力增大而增大,但增大幅度逐渐减小。出现上述趋势的原因是,透平机1、2、6的焓降均随着蒸发温度的升高而增大,从而做功量增多[22];随着蒸发压力升高,丙烷焓增量不断降低,使得丙烷质量流量不断增加[22],进而泵3的泵功逐渐增加,同时透平机6的做功也逐渐增加,但涨幅逐渐减小。而透平机1、2焓降的减少使得其做功减少,并且低蒸发温度又限制了循环的输出功,二者的共同作用下,出现了上述现象。由于循环总吸热量变化不大,因此热效率的变化趋势与净输出功相似。
|
图 3 系统净输出功在不同蒸发温度随蒸发压力的变化 Fig.3 Profiles of net output work of the system as a function of evaporation pressure under different evaporation temperatures |
|
图 4 系统热效率在不同蒸发温度随蒸发压力的变化 Fig.4 Thermal efficiency of the system as a function of evaporation pressure under different evaporation temperatures |
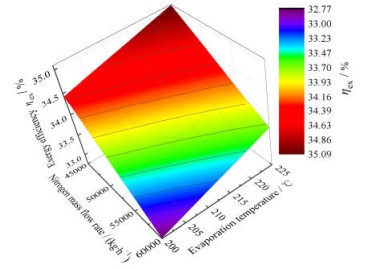
如图 5所示为氮气质量流量和蒸发温度对系统㶲效率的影响。从图 5中可以看出,系统㶲效率随着蒸发温度的升高而增大。而当氮气质量流量增加时,系统㶲效率呈现线性降低的趋势。由于规定了所有物流的进口温度和空气及循环水的出口温度,并且LNG出口温度也不发生变化,虽然循环水质量流量会随着二者的变化发生变化,但对总输入和总输出㶲的影响小于净输出功。所以㶲效率的变化趋势与净输出功大致相同。
|
图 5 氮气质量流量和蒸发温度对系统㶲效率的影响 Fig.5 Effects of nitrogen mass flow rate and evaporation temperature on system exergy efficiency |
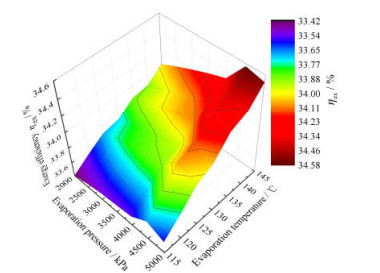
如图 6所示为蒸发温度和蒸发压力对系统㶲效率的影响。由图 6可知,系统㶲效率随着蒸发温度的升高而增加。蒸发压力的升高使得系统㶲效率出现了先增大后减小的变化趋势,且极值出现在4 500 kPa附近。随着蒸发温度升高,空气质量流量的增多使得总输入和总输出㶲均逐渐增大,但涨幅相差不大。因此㶲效率的变化受净输出功影响较大。即㶲效率的变化趋势与净输出功相似;同理,虽然蒸发压力的增大使得空气进出口㶲值增大,但涨幅对总输入和总输出㶲值影响不大,与此同时LNG出口㶲值的变化使得总输出㶲值呈现先增大后减小的趋势,综上所述,得出㶲效率随着蒸发压力的增大而先增大后减小的结论。
|
图 6 蒸发温度和蒸发压力对系统㶲效率的影响 Fig.6 Effects of evaporation temperature and evaporation pressure on system exergy efficiency |
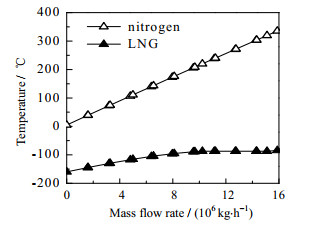
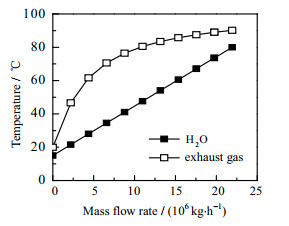
系统各设备的㶲损失系数、㶲损率以及㶲效率如表 3所示。通过对表中参数的综合分析,可以在对各设备的㶲损进行分析的同时,对系统的用能情况进行更全面的分析。例如,泵和透平机的㶲损率虽然较小,但二者的㶲损失系数都比较高,说明二者的用能较高。从表中可以看出,冷凝器1和换热器4的㶲损失系数较高,分别为44.75%和40.64%,并且冷凝器1的㶲损率最高,为52.85%。出现上述情况的原因是,热源和冷源之间的温度匹配程度不高。又因为LNG本身的㶲值较大,导致冷凝器1计算出来的㶲损较大,二者的综合使得其㶲损率最大;而泵和透平机除了有LNG㶲值较大这一原因之外,还因为其等熵效率被设置成定值75%。冷凝器1和换热器4的热交换过程见图 7和8。
|
|
表 3 系统各设备㶲分析 Table 3 Exergy analysis of each equipment |
|
图 7 冷凝器1的热交换过程 Fig.7 Heat exchange process of condenser 1 |
|
图 8 换热器4的热交换过程 Fig.8 Heat exchange process of heat exchanger 4 |
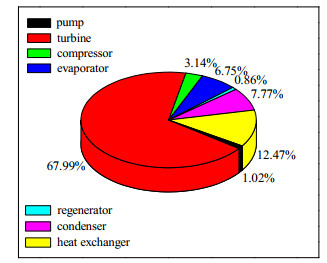
投资成本Cbm也是影响系统性能和技术应用的重要因素之一。对于本文提出的系统,其总投资成本包括设备投资成本、系统管理和运行成本。在LEC最低的情况下,各设备投资成本的比例如图 9所示。
|
图 9 各设备投资成本 Fig.9 Investment cost of each equipment |
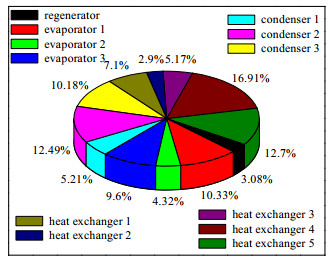
由图 9可知,透平机的投资成本最高,而回热的最低。压缩机由于在循环中具有较小的功率消耗和气体压缩压力,因此其投资成本不到5%;而透平机由于在循环中具有较高的气体膨胀压力,并且使用数量也较多,使得其投资成本最大。对于热交换设备,具体投资成本见图 10。从图 10中可知,换热器4投资成本最高,而换热器2最低。如果换热器中冷源与热源之间的温度较为匹配的话,在相同的传热系数下,那么换热器的面积就会较小,从而设备投资成本也会减少。而换热器2的投资成本最小,说明在乙烯-丙烷二级ORC中工质的选择较为合理。
|
图 10 各热交换设备投资成本 Fig.10 Investment cost of each heat exchange equipment |
经过模拟计算后得出,本文所提出的动力循环净输出功为2 834.1 kW,热效率为42.7%,㶲效率为35.1%。与同条件下的氮气回热Brayton与单级ORC联合动力循环相比,净输出功提高了30.6%,热效率提高了10%,㶲效率提高了5.6%。
4 结论本着高效利用LNG冷能的原则,本文提出了一种氮气回热Brayton循环与乙烯-丙烷二级ORC联合的冷热电三联供系统。使用数值模拟软件对系统性能进行模拟计算,得到如下结论:
(1) 设计了一种以LNG冷能为冷源,发电量达到2 834.1 kW,供热量和制冷量分别为6 138.5、1 368.2 kW的动力循环系统。由分析可知,提高氮气回热Brayton和ORC的蒸发温度以及降低氮气质量流量均有利于增大系统的发电量、热效率和㶲效率。当ORC蒸发温度小于125 ℃时,净输出功、热效率均在蒸发压力为4 000 kPa取得最佳值;当蒸发温度大于125 ℃时,二者均随蒸发压力的增大而增加,但变化幅度逐渐减小。系统㶲效率在此过程中先增大后减小,最佳蒸发压力为4 500 kPa。综合考虑热电的经济效益、设备投资成本、系统管理和运行成本,系统可带来的理想收益为4.21×106 $,折旧回收期为4.23 a。
(2) 提出的系统能够有效地梯级利用LNG的冷量,回收利用天然气燃烧后所释放的烟气,并对其中的CO2进行捕集,使能量得到充分利用。但冷凝器内冷热流温度匹配程度不高,导致其㶲损较大,同时系统㶲效率略低,有待提高改进。
| [1] |
中国能源网. 我国工业余热总资源占其燃料消耗总量的17%~67%[EB/OL]. [2020-05-20]. http://www.china5e.com/index.phpm=content&c=index&a=show&catid=13&id=870793. CHINA ENERGY NET. China's total industrial waste heat resources account for 17% to 67% of its total fuel consumption[EB/OL]. http://www.china5e.com/index.phpm=content&c=index&a=show&catid=13&id=870793, 2014-05-23. |
| [2] |
BAO J, LIN Y, ZHANG R, et al. Performance enhancement of two-stage condensation combined cycle for LNG cold energy recovery using zeotropic mixtures[J]. Energy, 2018, 8(157): 588-598. |
| [3] |
HE T, CHONG Z R, ZHENG J, et al. LNG cold energy utilization: prospects and challenges[J]. Energy, 2019, 3(170): 557-568. |
| [4] |
MA G, LU H, CUI G, HUANG K. Multi-stage Rankine cycle (MSRC) model for LNG cold-energy power generation system[J]. Energy, 2018, 12(165): 673-688. |
| [5] |
潘振, 仇阳, 乔伟彪, 等. 以燃煤废气为热源的LNG冷能三级利用系统[J]. 化工进展, 2016, 35(11): 3720-3726. PAN Z, QIU Y, QIAO W B, et al. LNG cold energy three-stage utilization system with coal-fired exhaust gas as heat source[J]. Progress in Chemical Industry, 2016, 35(11): 3720-3726. |
| [6] |
张丽, 马贵阳, 潘振, 等. 基于SAGD稠油开采余热利用的冷热电三联供系统[J]. 工程热物理学报, 2018, 39(9): 1890-1898. ZHANG L, MA G Y, PAN Z, et al. A combined cold and heat power supply system based on SAGD heavy oil recovery waste heat utilization[J]. Journal of Engineering Thermophysics, 2018, 39(9): 1890-1898. |
| [7] |
梁莹, 管延文, 蔡磊, 等. 利用LNG冷能与Brayton循环及ORC联合发电系统[J]. 煤气与热力, 2017, 37(12): 1-7. LIANG Y, GUAN Y W, CAI L, et al. Combined power generation system using LNG cold energy, Brayton cycle and ORC[J]. Gas and Heat, 2017, 37(12): 1-7. |
| [8] |
SUN Z, LAI J, WANG S, et al. Thermodynamic optimization and comparative study of different ORC configurations utilizing the exergies of LNG and low grade heat of different temperatures[J]. Energy, 2018, 3(147): 688-700. |
| [9] |
夏侯国伟, 白菲菲, 张早校. 以中低温余热为热源的LNG冷能利用流程改进[J]. 天然气工业, 2008(5): 112-114, 153. XIA H G W, BAI F F, ZHANG Z X. Improvement of LNG cold energy utilization process with middle and low temperature waste heat as heat source[J]. Natural Gas Industry, 2008(5): 112-114, 153. DOI:10.3787/j.issn.1000-0976.2008.05.038 |
| [10] |
WANG H, SHI X, CHE D. Thermodynamic optimization of the operating parameters for a combined power cycle utilizing 1ow-temperature waste heat and LNG cold energy[J]. Applied Thermal Engineering, 2013, 59(8): 490-497. |
| [11] |
AALI A, POURMAHMOUD N, ZARE V. Exergoeconomic analysis and multi-objective optimization of a novel combined flash-binary cycle for Sabalan geothermal power plant in Iran[J]. Energy Conversion & Management, 2017, 143(57): 377-390. |
| [12] |
ZHAO Y, WANG J. Exergoeconomic analysis and optimization of a flash-binary geothermal power system[J]. Applied Energy, 2016, 179(46): 159-170. |
| [13] |
WANG J, WANG J, DAI Y, et al. Thermodynamic analysis and optimization of a flash-binary geothermal power generation system[J]. Geothermics, 2015, 55(10): 69-77. |
| [14] |
GHOLIZADEH T, VAJDI M, MOHAMMADKHANI F. Thermodynamic and thermoeconomic analysis of basic and modified power generation systems fueled by biogas[J]. Energy Conversion and Management, 2018, 181: 463-475. |
| [15] |
ZAREH A D, SARAY R K, MIRMASOUMI S, et al. Extensive thermodynamic and economic analysis of the cogeneration of heat and power system fueled by the blend of natural gas and biogas[J]. Energy Conversion & Management, 2018, 164: 329-343. |
| [16] |
ZHANG L, PAN Z, ZHANG Z E, et al. Thermodynamic and economic analysis between organic Rankine cycle and Kalina cycle for waste heat recovery from steam-assisted gravity drainage process in oilfield[J]. Journal of Energy Resources Technology, 2018, 140(12): 1-13. |
| [17] |
BEJAN A. Thermal design and optimization[M]. New York: John Wiley & Sons, 1996.
|
| [18] |
MIGNARD D. Correlating the chemical engineering plant cost index with macro-economic indicators[J]. Chemical Engineering Research & Design, 2014, 92(2): 285-294. |
| [19] |
GUTHRIE K M. Data and techniques for preliminary capital cost estimating[J]. Chemical Engineering, 1969, 6(76): 114-142. |
| [20] |
ASHRAFI O, NAVARRI P, HUGHES R, et al. Heat recovery optimization in a steam-assisted gravity drainage (SAGD) plant[J]. Energy, 2016, 111(15): 981-990. |
| [21] |
张丽, 王文武, 张智恩, 等. 一种天然气液化和CO2捕集相结合的余热回收发电系统[J]. 化工学报, 2019, 70(1): 261-270. ZHANG L, WANG W W, ZHANG Z E, et al. A waste heat recovery power generation system combining natural gas liquefaction and CO2 capture[J]. CIESC Journal, 2019, 70(1): 261-270. |
| [22] |
仇阳, 潘振, 李萍, 等. 一种发电和天然气再液化相结合的LNG冷能利用系统[J]. 化工学报, 2017, 68(9): 3580-3591. QIU Y, PAN Z, LI P, et al. An LNG cold energy utilization system combined with power generation and natural gas re-liquefaction[J]. CIESC Journal, 2017, 68(9): 3580-3591. |




