半导体等行业的小型化和集成化带来的高热量问题严重影响了设备稳定性,成为限制行业发展的重要因素[1]。同时,半导体和微电子设备仍遵循经典的摩尔定律向减小特征尺寸、增加晶体管密度的方向发展[2],导致单位面积下的热流密度急剧增长,如目前超级计算机芯片的热流密度[3]已经达到100 W·cm−2、固体激光器内部局部热流密度[4]超过1 000 W·cm−2。大热流密度下引起的内部高温严重影响了设备的运行效率和稳定性,计算机设备核心器件温度的经验法则指出当电子元件的结温(半导体芯片的最高温度)每降低10 ℃,故障率就可减半[5]。然而传统的散热方式(强制风冷、液冷等)难以满足该类设备的散热需求。在这样的背景下,微通道技术、多孔介质、热管技术、喷雾冷却等新型传热技术受到了越来越多的关注[6-9]。相较于其他散热方式,喷雾冷却技术具有传热系数高、冷却工质用量小、冷却均匀、成本低等优点,被认为是未来解决高功率设备器件散热问题最有效的方式之一。
喷雾冷却技术是在压力作用下,将冷却工质雾化成小液滴而喷射至热沉表面上,并形成一层薄液膜,通过液滴冲击、液膜的蒸发和对流等过程带走热沉表面的热量[10]。但目前针对该技术的研究大都集中在应用探究[11-12]和传热性能实验研究[13-14],对喷雾冷却系统传热性能进行模拟计算的研究相对较少。数值模拟方法能够呈现喷雾冷却过程中的流体力学和传热过程细节,结合实验再通过模拟研究来优化操作变量值,从而实现过程的调控,成为喷雾冷却传热过程研究的重要手段。Liu等[15]以水为冷却工质,基于欧拉-拉格朗日(Euler-Lagrange,E-L)法建立了喷雾冷却单相区的数理模型,通过与实验数据对比证实了模型的可靠性。Yan等[16]和Cai等[17]拓展了Liu的研究,以水和乙醇-水混合物为冷却工质,建立了从单相区到核态沸腾区的喷雾冷却系统数理模型,发现核态沸腾区比单相区的液膜薄,传热系数随喷雾高度的增加而减小、随喷雾压力的增大而增大。鲁森等[18]在单相区数值模拟过程中发现表面温度由圆心沿径向逐渐升高,且温度分布随喷雾体积流量的增大均匀性变差。侯燕[19]在研究喷嘴数量对换热的影响过程中发现当喷雾底部与热沉表面外切时传热效果最好,此时喷嘴高度为最优高度。
综上,目前对喷雾冷却系统的数值模拟主要考察单因素对传热效果的影响,缺乏对多种因素的共同考察及多因素中不同因素对传热效果的影响程度。本研究基于某小型喷雾冷却实验系统开发需要,采用计算流体力学(computational fluid dynamics,CFD)方法建立喷雾冷却系统数理模型,通过数值模拟研究多个操作参数对喷雾冷却单相区传热的影响规律,指导小型喷雾冷却实验系统的设计和操作。
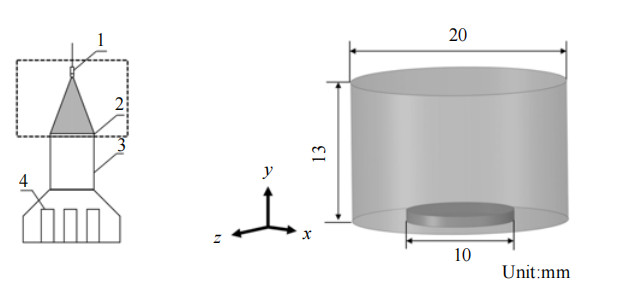
2 几何模型及数值计算方法 2.1 几何模型基于小型喷雾冷却系统的设计要求,本研究选择文献[20]数据为依据建立物理模型,如图 1所示。计算域为直径20 mm、高13 mm的圆柱体区域,其中计算域底部热沉为直径10 mm、厚度1 mm的固体域,热沉底部以固定热流密度进行加热,液滴从喷嘴喷出后在热沉上形成液膜并进行换热。
|
图 1 喷雾冷却示意图[20]及物理模型 Fig.1 Schematic diagram and physical model of the spray cooling system[20] 1.nozzle 2.heat sink 3. heating device 4.thermocouple |
模拟对象为计算域内的喷雾和气体。数学模型主要包括连续相、湍流模型和离散相模型。
2.2.1 连续相模型对于计算域中的气相与液膜采用连续相模型进行模拟,连续相控制方程包括质量、动量、能量方程及组分输运方程,如式(1)~(4)所示。
| $ \nabla \cdot (\rho \mathit{\boldsymbol{u}}) = \Delta m $ | (1) |
式中:
| $ \frac{{\partial (\rho \mathit{\boldsymbol{u}})}}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{uu}}} \right) = - \nabla p + \nabla \cdot [\mu (\nabla \mathit{\boldsymbol{u}} + \nabla {\mathit{\boldsymbol{u}}^{\rm{T}} })] + \rho \mathit{\boldsymbol{g}} + \Delta \mathit{\boldsymbol{u}} $ | (2) |
式中:t为时间,s;μ为黏度,Pa·s;p为压力,Pa;T为转置;g为重力加速度矢量,m·s−2;
| $ \frac{{\partial (\rho T)}}{{\partial t}} + \nabla \cdot (\rho \mathit{\boldsymbol{u}}T) = \nabla \cdot (\frac{{{k_{{{\rm{eff}}} }}}}{{{c_p}}}\nabla T) + \Delta E $ | (3) |
式中:T为热力学温度,K;keff为流体的有效传热系数,W·m−2·K−1,其中keff=kl+kt;kl为流体的传热系数,W·m−2·K−1;kt为湍流引起的传热系数,W·m−2·K−1;cp为流体的比定压热容,J·kg−1·K−1;
| $ \frac{\partial }{{\partial t}}(\rho {w_f}) + \nabla \cdot (\rho \mathit{\boldsymbol{u}}{w_f}) = - \nabla \cdot {\mathit{\boldsymbol{J}}_\mathit{\boldsymbol{f}}} + {S_f} $ | (4) |
式中:wf为组分f的质量分数,2种组分分别为空气和水蒸气;Jf为组分f的扩散通量矢量,kg·m−3·s−1;Sf为由于蒸发引起组分增加的源项,kg·m−3·s−1。
2.2.2 湍流模型湍流模型选用Realizable k-ε模型,输运方程[21]为
| $ \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {L_x}}}(\rho k{\mathit{\boldsymbol{u}}_{{{\rm{l}}} , x}}) = \frac{\partial }{{\partial {L_z}}}[(\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}})\frac{{\partial k}}{{\partial {L_z}}}] + {G_k} - \rho \varepsilon $ | (5) |
| $ \frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial {L_x}}}(\rho \varepsilon {\mathit{\boldsymbol{u}}_{{{\rm{l}}} , x}}) = \frac{\partial }{{\partial {L_z}}}[(\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}})\frac{{\partial \varepsilon }}{{\partial {L_z}}}] + \rho {C_1}\Delta \varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {{\mathit{\boldsymbol{u}}_{\rm{n}} }\varepsilon } }} $ | (6) |
| $ {C_{\text{1}}} = {\max _{}}(0.43{, _{}}\frac{\eta }{{\eta + 5}}) $ | (7) |
| $ \eta = {{(k} \mathord{\left/ {\vphantom {{(k} \varepsilon }} \right. } \varepsilon })\sqrt {2{\mathit{\boldsymbol{E}}_{xz}} \cdot {\mathit{\boldsymbol{E}}_{xz}}} $ | (8) |
| $ {\mathit{\boldsymbol{E}}_{xz}} = \frac{1}{2}(\frac{{\partial {\mathit{\boldsymbol{u}}_{{{\rm{l}}} , z}}}}{{\partial {L_x}}} + \frac{{\partial {\mathit{\boldsymbol{u}}_{{\rm{l}}, x}}}}{{\partial {L_z}}}) $ | (9) |
式中:ul, x为水平方向沿x方向分速度矢量,m·s−1;ul, z为水平方向沿z方向分速度矢量,m·s−1;un为垂直方向分速度矢量,m·s−1;Lx为x方向位移量,m;Lz为z方向位移量,m;μt为湍流黏度,Pa·s;σk、σε分别为湍动能k、耗散率ε对应的Prandtl数;
离散相模型主要包括液滴雾化模型、液滴追踪模型、壁面液膜模型。结合实验系统使用的喷嘴数据,本研究选用基于E-L法的离散相模型(discrete phase model,DPM)中的solid-cone(实心锥喷嘴)雾化模型。
液滴追踪模型通过对液滴所受力的平衡进行积分预测其运动轨迹,该力平衡在拉格朗日坐标系下进行描述:
| $ \frac{{d{\mathit{\boldsymbol{u}}_{\rm{d}}}}}{{dt}} = \frac{{(\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{u}}_{\rm{d}}})}}{{{\tau _{\rm{r}}}}} + \frac{{\mathit{\boldsymbol{g}}({\rho _{\rm{d}}} - \rho )}}{{{\rho _{\rm{d}}}}} $ | (10) |
| $ {\tau _{\rm{r}}} = \frac{{{\rho _{\rm{d}}}d_{\rm{d}} ^2}}{{3\mu }}\frac{4}{{{C_{\rm{d}} }Re}} $ | (11) |
| $ {C_{\rm{d}}} = {C_{{{\rm{d}}} , {\rm{s}}}}\left( {{\text{1 + 2}}{\text{.632}}y} \right) $ | (12) |
| $ Re = \frac{{\rho {d_{\rm{d}}}\left| {{\mathit{\boldsymbol{u}}_{\rm{d}}} - \mathit{\boldsymbol{u}}} \right|}}{\mu } $ | (13) |
| $ {C_{{\rm{d, s}}}} = \left\{ {\begin{array}{*{20}{c}} {{\text{0}}{\text{.424}}}&{Re{\text{ > }}{1_{}}000} \\ {\frac{{24}}{{Re}}\left( {1 + \frac{1}{6}R{e^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}}} \right)}&{Re \leqslant {1_{}}000} \end{array}} \right. $ | (14) |
式中:ud为液滴的速度矢量,m·s−1;ρd为液滴密度,kg·m−3;
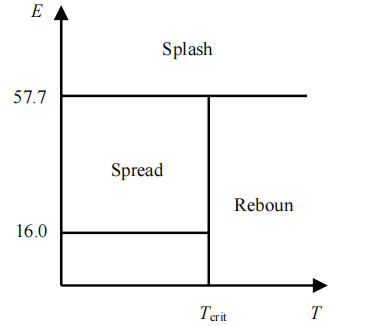
壁面液膜模型选用Lagrange壁膜模型,液滴与壁面间的作用方式由液滴的撞击动能E(J)和临界温度Tcrit(K)决定,见图 2。
| $ E = \frac{{{\rho _{\rm{d}}}{\mathit{\boldsymbol{u}}_{{\rm{n}} , {\rm{d}} }}{d_{\rm{d}}}}}{\sigma }[\frac{1}{{{{\min }_{}}({{{h_0}} \mathord{\left/ {\vphantom {{{h_0}} {{d_{\rm{d}}}}}} \right. } {{d_{\rm{d}}}}}, 1) + {{{\delta _{{\rm{bl}}}}} \mathord{\left/ {\vphantom {{{\delta _{{\rm{bl}}}}} {{d_{\rm{d}}}}}} \right. } {{d_{\rm{d}}}}}}}] $ | (15) |
| $ {\delta _{{{\rm{bl}}} }} = \sqrt {{d_{\rm{d}}}\mu /({\rho _{\rm{d}}}{\mathit{\boldsymbol{u}}_{{\rm{n}} , {\rm{d}} }})} $ | (16) |
| $ {T_{{\rm{crit}}}} = T_{{{\rm{cri}}} {\text{t}}}^*{T_{{{\rm{sat}}} }} $ | (17) |
|
图 2 液滴撞击壁面后状态 Fig.2 State distribution after droplet impact on wall |
式中:un, d为液滴垂直壁面方向的速度矢量,m·s−1;σ为表面张力,N·m−1;h0为液膜厚度,m;
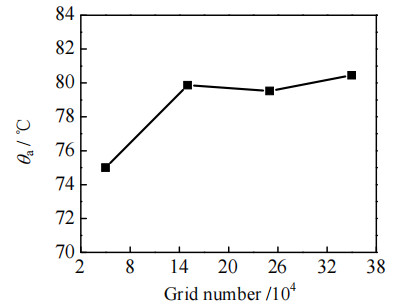
采用非结构网格,选取4种不同密度的网格进行模拟验证,结果见图 3。从图中可以看出,当网格数量大于15万后,热沉表面平均温度θa温差小于1 ℃,此时网格数基本不影响计算结果。因此本研究使用15万的网格进行模拟计算。
|
图 3 网格无关性验证 Fig.3 Grid independence verification |
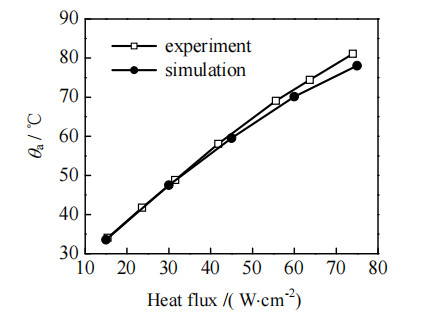
利用文献[20]数据进行模型可靠性验证,选取喷嘴高度为8.67 mm、喷射速度为28.60 m·s−1、喷雾锥角60°、冷却工质温度为20 ℃、液滴平均直径为0.085 3 mm、喷雾体积流量为4.95 L·h−1的体系进行模型验证,所得热沉表面平均温度的模拟值与实验值的对比如图 4所示。从图中可以发现,模拟值与实验值变化趋势基本一致,最大相对误差为3.7%,说明本研究所建模型可靠。
3 结果与讨论本节研究喷雾体积流量qV(L·h−1)、喷雾高度h(mm)、工质温度θw(℃)对喷雾冷却传热性能影响;并采用正交试验法对喷雾体积流量、喷雾高度、工质温度、热流密度q(W·cm−2) 4个因素的影响进行分析,优选操作参数。
3.1 单因素影响分析取热流密度为45 W·cm−2,分别讨论单因素参数(喷雾体积流量、喷雾高度、工质温度)对喷雾冷却系统单相区传热性能的影响。选取的喷嘴高度为8.67 mm、喷射速度为28.60 m·s−1、冷却工质温度为20 ℃、液滴平均直径为0.085 3 mm、喷雾体积流量为4.95 L·h−1。
3.1.1 喷雾体积流量影响其他参数不变,模拟得到不同喷雾体积流量下热沉表面的温度分布,见图 5。图中D为表面不同位置距热沉中心距离,热沉中心为原点,从图中可以发现,热沉表面平均温度随着喷雾体积流量的增大逐步下降。这是由于喷雾体积流量的增大使单位时间内撞击热沉表面及液膜的冷却工质液滴数量增多,液膜内的湍流程度加强,加快了液膜的更新速度,强化了液膜与液滴、液膜与壁面之间的对流传热,提高了喷雾冷却系统传热性能。从图 5(b)可知,当喷雾体积流量较小(≤9.90 L·h−1)时,热沉表面温度θs分布呈现中心低并沿径向逐渐升高的特征;当喷雾体积流量较大(≥14.85 L·h−1)时,表面温度分布逐渐呈现“W”型,中心温度较高,沿径向先降低后升高的特征。

|
图 5 不同喷雾体积流量的热沉表面温度图 Fig.5 Surface temperatures of heat sink at different spray flow rates |
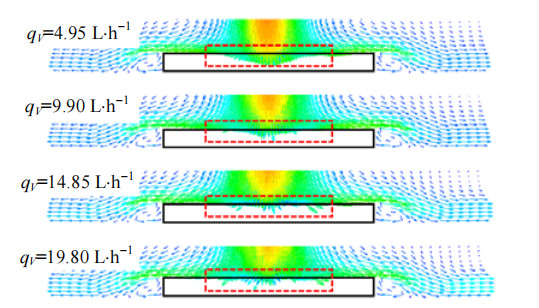
结合热沉表面附近速度场分布(见图 6)讨论体积流量对温度分布影响。从图中可以发现,当喷雾体积流量较小时(4.95、9.90 L·h−1),热沉表面中心区域的液滴速度整体最大,液滴速度越大对液膜的扰动越强,因此中心区域传热效果更好,表面温度呈现中心低并沿径向逐渐升高的特征;随着喷雾体积流量增大(14.85、19.80 L·h−1),热沉表面中心区域的液滴速度相对两侧较小,这是由于喷雾体积流量增大使液滴通量增大,使喷雾过程中的液滴呈现出中心密度大边缘密度小的特征,导致中心区域液滴数目急剧增多,强化了液滴间的相互作用,使中心区域的液滴速度衰减更快,造成表面温度呈现中心温度较高,沿径向先降低后升高的“W”型分布特征。
|
图 6 不同喷雾体积流量下的热沉表面附近喷雾速度场分布 Fig.6 Distribution of spray velocity field near heat sink surface under different spray flow rates |
其他参数不变,改变不同的喷雾高度(6~12 mm),为保证冷却工质的利用率最高、传热效果最佳,对喷雾锥角进行调整(79.6°~45.2°),使喷雾形成的圆形区域与热沉表面相切[22]。
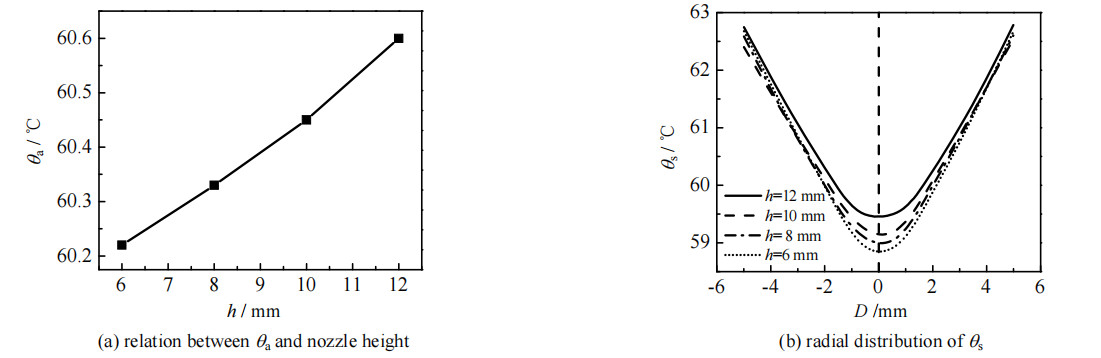
图 7为不同喷雾高度下热沉表面平均温度及温度径向分布。从图 7(a)中可以发现,当喷雾高度增大时,表面平均温度也随之升高。这是由于随着喷雾高度的增大,一方面液滴分散程度增大,液滴间的相互作用减小,一定程度上抑制了液滴衰减程度;另一方面液滴与空气间相互作用增强,又加剧了液滴动量的衰减。两方面共同作用使热沉表面平均温度变化幅度很小,如当喷雾高度从6 mm上升至12 mm时,热沉表面平均温度由60.22 ℃增大至60.60 ℃,温度仅升高0.38 ℃。
|
图 7 不同喷雾高度的热沉表面温度图 Fig.7 Surface temperatures of heat sink at different spray heights |
从图 7(b)中可以发现,不同喷雾高度的中心区域温度差距相对较大,边缘处温度非常接近;当喷雾高度为6 mm时,表面温度在中心区域附近最小。这是由于相对其他区域,喷雾中心区域液滴密度最高、液滴间的相互影响更为剧烈;随着喷雾高度的增大,中心区域液滴密度下降程度更大,减缓了液滴间相互作用,抑制了中心区域液滴的速度衰减,造成液滴撞击液膜时具有更高的速度、液膜的湍流程度增强,强化了该区域的传热过程。因此喷雾高度较高时,热沉表面中心温度变化更为剧烈。
3.1.3 工质温度影响图 8为不同工质温度下热沉表面平均温度及表面温度径向分布。从图中可以发现,当工质温度由10 ℃上升至25 ℃,壁面平均温度由53.5 ℃上升至63.3 ℃,此外表面平均温度随工质温度升高几乎线性增加。

|
图 8 不同工质温度的热沉表面温度图 Fig.8 Surface temperatures of heat sink at different fluid temperatures |
这是由于工质温度的升高使液滴撞击热沉表面后形成的液膜温度升高,液膜与壁面温差减小,传热推动力下降,热沉表面平均温度升高;不同工质温度的表面温度分布趋势一致,均呈现中心温度低并沿径向逐渐升高的特征。
3.2 正交模拟试验优化喷雾冷却操作参数本研究中影响热沉表面平均温度的4个因素为喷雾体积流量qV、喷雾高度h、工质温度θw、热流密度q,结合正交试验表的特点,建立五因素四水平表,将其中一个因素设为空列,正交模拟试验方案如表 1所示。
|
|
表 1 正交模拟试验因素水平表 Table 1 Factors and levels of orthogonal simulation tests |
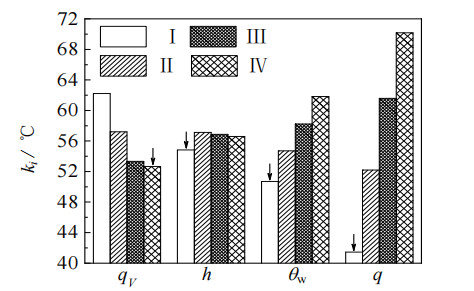
在本研究中,模拟获得的热沉表面平均温度θa越低,代表该体系下传热效果越好,因此优水平对应ki(同水平下表面平均温度均值,℃)最小的水平。正交模拟结果见图 9,由图可知,在装置允许操作参数范围内,最优组合为喷雾体积流量19.80 L·h−1、喷雾高度6 mm、工质温度10 ℃、热流密度30 W·cm−2。
|
图 9 影响因素与ki图 Fig.9 Plot of affecting factors ~ indicator ki |
正交模拟计算所得偏差平方和S、自由度F、自由度统计量Fs,自由度临界值Fc与显著性结果见表 2。对因素进行F-检验时,一般考虑4种情况,其中F0.01(3, 3)、F0.05(3, 3)、F0.1(3, 3)表示影响因素的自由度F和空列自由度分别为3时,影响因素水平发生改变,对实验结果产生显著影响的可能性为99%、95%、90%的Fc值。
|
|
表 2 不同因素的Fs和显著性 Table 2 Fs statistics and significance of different factors |
(1) Fs≥F0.01(3, 3) =29.46,即Fs≥29.46,则因素对结果的影响“高度显著”;
(2) 9.28=F0.05(3, 3)≤Fs<F0.01(3, 3),即9.28≤Fs < 29.46,则因素对结果的影响为“显著”;
(3) 5.39=F0.1(3, 3) ≤Fs < F0.05(3, 3),即5.39≤Fs < 9.28,则因素对结果有“一定影响”;
(4) Fs < F0.05(3, 3)=5.39,Fs < 5.39则因素对结果“无影响”。
结合表 2可见,对表面温度影响的显著程度排序为:热流密度 > 工质温度 > 喷雾体积流量 > 喷雾高度,且热流密度、工质温度及喷雾体积流量对表面温度均为高度显著,喷雾高度为无影响。因此,为降低喷雾冷却系统中热沉表面的温度,应在实验系统允许的条件下减小热沉底部热量的加入、使用温度更低的冷却工质并增大工质的流量,而喷雾高度对实验影响很小,可根据实验具体需要进行选择。
4 结论针对某小型喷雾冷却系统开发的需要,采用欧拉-拉格朗日方法,设计开发了喷雾冷却系统数理模型,采用CFD方法开展模拟研究,结论如下:
(1) 单因素模拟结果表明:热沉表面平均温度随喷雾体积流量的增大而减小,随喷雾高度增加、工质温度升高而增大;当喷雾体积流量较小时,表面温度呈现中心低并沿径向逐渐升高的特征;当喷雾体积流量较大时,表面温度呈现中心温度较高、沿径向先降低后升高的特征;不同喷雾高度、工质温度的表面温度均呈现中心温度低并沿径向逐渐升高的特征。
(2) 正交模拟结果表明:对表面平均温度影响的显著程度排序为:热流密度 > 工质温度 > 喷雾体积流量 > 喷雾高度。在当前装置及工况条件下,喷雾冷却实验系统的建议操作参数为:喷雾体积流量为19.80 L·h−1、喷雾高度为6 mm、工质温度为10 ℃、热流密度为30 W·cm−2。
| [1] |
SMAKULSKI P, PIETROWICZ S. A review of the capabilities of high heat flux removal by porous materials, microchannels and spray cooling techniques[J]. Applied Thermal Engineering, 2016, 104: 636-646. DOI:10.1016/j.applthermaleng.2016.05.096 |
| [2] |
MOORE E G. Cramming more components onto integrated circuits[J]. Proceedings of the IEEE, 1998, 86(1): 82-85. DOI:10.1109/JPROC.1998.658762 |
| [3] |
LIANG G T, MUDAWAR I. Review of spray cooling-Part 1: Single-phase and nucleate boiling regimes, and critical heat flux[J]. International Journal of Heat and Mass Transfer, 2017, 115: 1174-1205. DOI:10.1016/j.ijheatmasstransfer.2017.06.029 |
| [4] |
ZHANG L Y, ZHANG Y F, CHEN J Q, et al. Fluid flow and heat transfer characteristics of liquid cooling microchannels in LTCC multilayered packaging substrate[J]. International Journal of Heat and Mass Transfer, 2015, 84: 339-345. DOI:10.1016/j.ijheatmasstransfer.2014.12.079 |
| [5] |
CENGEL A Y. Heat transfer: A practical approach[M]. New York: McGraw-Hill, 2003.
|
| [6] |
宗露香, 徐进良, 刘国华. 微通道内流动沸腾不稳定性影响因素实验研究[J]. 高校化学工程学报, 2015, 29(1): 90-95. ZONG L X, XU J L, LIU G H. Experimental study on the flow boiling instability governing parameters in microchannels[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(1): 90-95. DOI:10.3969/j.issn.1003-9015.2015.01.013 |
| [7] |
潘艳秋, 张春超, 高石磊, 等. 基于热流固耦合的微通道冷却系统模拟[J]. 天津大学学报(自然科学与工程技术版), 2022, 55(4): 364-370. PAN Y Q, ZHANG C C, GAO S L, et al. Simulation of microchannel cooling system based on thermal-fluid-solid coupling[J]. Journal of Tianjin University(Science and Technology), 2022, 55(4): 364-370. |
| [8] |
TAHMASBI M, SIAVASHI M, NOROUZI M A, et al. Thermal and electrical efficiencies enhancement of a solar photovoltaic-thermal/air system (PVT/air) using metal foams[J]. Journal of the Taiwan Institute of Chemical Engineers, 2021, 124: 276-289. DOI:10.1016/j.jtice.2021.03.045 |
| [9] |
张伟龙, 魏新利, 关中杰, 等. 有/无泵辅助板式蒸发器环路热管系统性能的实验研究[J]. 高校化学工程学报, 2018, 32(6): 1299-1306. ZHANG W L, WEI X L, GUAN Z J, et al. Experimental study on plate evaporator loop-heat-pipe systems with/without pump-assistance[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(6): 1299-1306. DOI:10.3969/j.issn.1003-9015.2018.06.008 |
| [10] |
KIM J G. Spray cooling heat transfer: The state of the art[J]. International Journal of Heat & Fluid Flow, 2007, 28(4): 753-767. |
| [11] |
XU X J, WANG Y, JIANG Y L, et al. Recent advances in closed loop spray cooling and its application in airborne systems[J]. Journal of Thermal Science, 2021, 30(1): 32-50. DOI:10.1007/s11630-020-1395-y |
| [12] |
AMIRHOSEIN H, MEHRAN R Z, SAMAN R. An efficient pulsed-spray water cooling system for photovoltaic panels: Experimental study and cost analysis[J]. Renewable Energy, 2021, 164: 867-875. DOI:10.1016/j.renene.2020.09.021 |
| [13] |
LIU P F, KANDASAMY R, FENG H C, et al. Influence of air on heat transfer of a closed-loop spray cooling system[J]. Experimental Thermal and Fluid Science, 2020, 111: 109903. DOI:10.1016/j.expthermflusci.2019.109903 |
| [14] |
LIU N, YU Z X, ZHU T H, et al. Effects of micro-structured surface and mixed surfactants on the heat transfer performance of pulsed spray cooling[J]. International Journal of Thermal Sciences, 2020, 158: 106530. DOI:10.1016/j.ijthermalsci.2020.106530 |
| [15] |
LIU H, CAI C, YAN Y A, et al. Numerical simulation and experimental investigation on spray cooling in the non-boiling region[J]. Heat and Mass Transfer, 2018, 54(12): 3747-3760. DOI:10.1007/s00231-018-2402-7 |
| [16] |
YAN P L, CAI C, LIU H, et al. Numerical simulation on multiphase spray cooling: 1st International Global on Renewable Energy and Development [C]. Singapore: IOP Publishing, 2017.
|
| [17] |
CAI C, LIU H, JIA M, et al. Numerical investigation on heat transfer of water spray cooling from single-phase to nucleate boiling region[J]. International Journal of Thermal Sciences, 2020, 151: 106258. DOI:10.1016/j.ijthermalsci.2019.106258 |
| [18] |
鲁森, 王延遐, 沈玉凤, 等. 喷雾冷却在单相区中换热特性的数值模拟研究[J]. 热科学与技术, 2017, 16(1): 34-39. LU S, WANG Y X, SHEN Y F, et al. Numerical simulation of heat transfer characteristics of spray cooling in single-phase region[J]. Journal of Thermal Science and Technology, 2017, 16(1): 34-39. |
| [19] |
侯燕. 多喷嘴喷雾冷却实验研究与数值模拟[D]. 北京: 中国科学院工程热物理研究所, 2014. HOU Y. The experimental study and numerical simulation of multi-nozzle spray cooling [D]. Beijing: Institute of Engineering Thermophysics, Academia Sinica, 2014. |
| [20] |
王亚青, 刘明侯, 刘东, 等. 大功率激光器喷雾冷却中无沸腾区换热性能实验研究[J]. 中国激光, 2009, 36(8): 1973-1978. WANG Y Q, LIU M H, LIU D, et al. Experiment study on non-boiling heat transfer performance in spray cooling for high-power laser[J]. Chinese Journal of Lasers, 2009, 36(8): 1973-1978. |
| [21] |
王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. WANG F J. Computational fluid dynamics analysis: Principle and application of CFD software[M]. Beijing: Tsinghua University Press, 2004. |
| [22] |
VISARIA M, MUDAWAR I. A systematic approach to predicting critical heat flux for inclined sprays[J]. Journal of Electronic Packaging, 2007, 129(4): 452-459. DOI:10.1115/1.2804095 |