2. 中山大学 化学与化学工程学院,广东省石化过程节能工程技术研究中心,广东 广州 510275
2. Guangdong Engineering Technology Research Center for Petrochemical Energy Conservation, School of Chemical Engineering and Technology, Sun Yat-sen University, Guangzhou 510275, China
塔间热集成是利用两塔之间冷热工艺物流热交换,以实现能量匹配利用,同时可减少冷热公用工程消耗[1]。研究手段分为基于知识的传统方法、数学方法及传统法与数学法相结合的方法[2]。非集中式塔间热集成常利用经验规则来确定。首先确定包括塔再沸及冷凝物流的出口和返塔温度、换热量等参数,然后借助夹点或数学规划的方法设计换热网络。在集成系统优化中,流量、进出口温度并非定值,而是作为待优化的参量。如塔压变化时,物流起始温度和目标温度均随塔压呈一定规律的变化。因而可考虑将换热网络优化和精馏塔的塔压同时优化。
以往研究塔压作为定值或离散优化,并未真正实现塔压参数与换热网络的同步集成优化。如湛世辉等[3]绘制了苯乙烯装置各精馏塔的温焓图,提出了直接热集成、调压热集成和双效精馏与间接热集成耦合等3种方案。结果表明采用调压热集成措施能明显降低操作费用。李春妍等[4]应用差压热集成技术精制高纯戊烷,可实现系统节能。案例表明,与常规精馏过程相比,差压热集成系统的总能耗降低了38.1%。Aly[5]在热集成启发式规则的基础上使一个塔的塔顶物流与另一塔的塔底物流换热,研究了若干塔间的调压热集成,但未考虑存在合适温差下的塔间直接热集成。汪旭和冯霄[6]提出了一种将模拟分析技术和启发式方法相结合的塔系热集成方法,建立了三条热集成规则的热集成矩阵,同时考虑了精馏塔间的直接热集成和调压热集成。该方法可筛选出可行且有效的热集成方案。钱新华等[7]基于模拟技术,通过灵敏度分析得到精馏塔各操作参数的样本映射数据,拟合参数关联的多项式方程,基于遗传算法及模式搜索设计过程费用函数,提出了将模拟分析技术与随机搜索算法相结合的能量集成方法,该方法以过程费用函数最小化为优化目标。孙艳泽和冯霄[8]根据各工况对应的夹点位置,扩展了夹点设计原则,提出了不同操作工况的装置热集成方法,可使装置中固定不变部分换热网络结构相同,且在不同工况下装置的换热网络始终是最大能量回收网络。李玉刚等[9]针对宽沸程物系分离的特点,将浓度从进料到产品分段,每段对应一个精馏塔操作,通过调整各塔的出料浓度、操作压力,实现各塔间的热集成。吴孟兵[10]针对戊烷装置比较了常规精馏和热集成精馏两种工艺,并利用化工过程模拟软件Aspen Plus对两种方案进行了模拟优化,确定了各自的最优操作条件。通过对比,热集成精馏工艺比常规精馏节约能耗33.3%。韩祯等[11]采用Aspen Plus及修正的Wilson模型模拟了压力对乙酸异丙酯-异丙醇物系共沸组成的影响,提出该物系基于热集成的变压精馏工艺,研究了系统能耗随变压精馏工艺两塔压力组合的变化趋势,优化了理论塔板数、进料位置、回流比等操作参数。Andrecovich和Westerberg[12]假设每个塔都是清晰分割,提出了带热集成的简单塔序列综合问题的系统性超结构方法。王克峰等[13]采用神经元网络法和遗传算法,在过程系统用能一致性的基础上对分离系统与换热网络同步优化提出了改进的优化模型及优化策略。该方法能迅速地同步得到分离序列与换热网络的流程结构与操作参数。
本文结合多尺度集成策略与建模方法[14],以乙苯装置的干气和乙苯精制过程的精馏系统作为案例,首先给出热集成物流筛选的启发式规则,然后建立塔压与物流温度的约束方程,将该方程与以年度总费用为目标函数的换热网络混合整数非线性模型耦合,同时优化塔压参数及相应的换热网络,最后讨论塔压作为耦合变量对塔间热集成的作用机制。
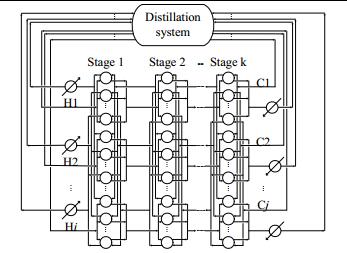
2 问题描述将精馏塔系及相应的换热网络定义为集成系统,如图 1所示。精馏塔的操作参数通常可在一定的范围内波动,将有调节幅度的变量作为过程集成的关键优化变量。本文的模型以文献[15]的换热网络模型为基础,超结构级数 (Nk) 满足:
| $ {\rm{min}}({N_{\rm{h}}}, {N_{\rm{c}}}) \le {N_k} \le {\rm{max}}({N_{\rm{h}}}, {N_{\rm{c}}}) $ | (1) |
|
图 1 精馏系统与换热网络间相互连接关系 Fig.1 Schematic diagram of interconnection between distillation system and heat exchanger network |
为简化模型作如下假设:(1) 流股等温混合;(2) 冷公用工程为循环水,热公用工程为相应等级蒸汽;(3) 塔压和物流温度存在一定的函数约束,可简化为线性关系。
3 数学模型 3.1 耦合塔压变量的同时优化模型将年度总费用 (TAC) 作为目标函数,见式 (2),TAC为公用工程的消耗费用和换热器投资费用之和。
| $ $\begin{array}{l} {\rm{min }}Obj{\rm{ }} = \left[{h\left( {\sum\limits_{i \in HP} {CCUqc{u_i} + \eta \sum\limits_{j \in CP} {CHUqh{u_j}} } } \right)} \right] + \\ \frac{{\sum\limits_{{\rm{i}} \in {\rm{HP}}} {\sum\limits_{j \in CP} {\sum\limits_{k \in ST} {C{F_{i, j}}{Z_{i, j, k}}} + \sum\limits_{i \in HP} {\sum\limits_{j \in CP} {\sum\limits_{K \in ST} {\left\{ {{C_{i, j}}{{\left[{{q_{i, j, k}}/\left( {{U_{i, j}}LMT{D_{i, j, k}}} \right)} \right]}^{{B_{ij}}}}} \right\}} } } } } }}{{pt}} + \\ \frac{{\sum\limits_{i \in HP} {C{F_{i, CU}}{Z_{CU, i}}} + \sum\limits_{i \in HP} {\left\{ {{C_{i, CU}}{{\left[{qc{u_i}/\left( {{U_{i, CU}}LMT{D_{i, CU}}} \right)} \right]}^{{B_{i, CU}}}}} \right\}} }}{{pt}} + \\ \frac{{\sum\limits_{i \in HP} {C{F_{i, HU}}} + {C_{i, HU}}{{\left[{{q_{i, HU}}/\left( {{U_{i, HU}}LMT{D_{i, HU}}} \right)} \right]}^{{B_{i, HU}}}}}}{{pt}} \end{array}$ $ | (2) |
各物流总的热平衡、各换热级热平衡、进口温度定义、温度的单调变化约束、冷热公用工程方程,逻辑性约束、最小温差及必要的变量边界约束分别见参考文献[14]中的方程 (3)~(10)。热集成系统中热物流为塔顶蒸汽。塔压变化导致塔顶蒸汽的起始及终了温度发生相应变化。
| $ \left\{ \begin{array}{l} TI{N_i} = f\left( {{P_i}} \right)\\ TOU{T_i} = g\left( {{P_i}} \right)\\ TI{N_{i, b}} = L({P_i})\\ TOU{T_{i, b}} = O({P_i})\\ {\left( {{P_i}} \right)_{{\rm{Lower}}}} \le {P_i} \le {\left( {{P_i}} \right)_{{\rm{Upper}}}} \end{array} \right. $ | (3) |
变量的边界调整为:
| $ \left\{ \begin{array}{l} {\left( {TI{N_i}} \right)_{{\rm{Lower}}}} \le TI{N_i} \le {\left( {TI{N_i}} \right)_{{\rm{Upper}}}}\\ {\left( {TOU{T_i}} \right)_{{\rm{Lower}}}} \le TOU{T_i} \le {\left( {TOU{T_i}} \right)_{{\rm{Upper}}}} \end{array} \right. $ | (4) |
传热温差采用Chen近似计算方法:
| $ LMT{D_{i, j, k}} = {\left[{\left( {d{t_{i, j, k}}} \right)\left( {d{t_{i, j, k + 1}}} \right)\frac{{d{t_{i, j, k}} + d{t_{i, j, k + 1}}}}{2}} \right]^{\frac{1}{3}}} $ | (5) |
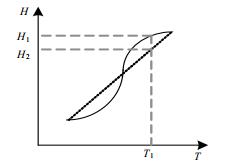
温度和焓值之间的函数关系式为非线性,特别是对于化工过程中常见的有虚拟组成表示的复杂混合物,同时也要考虑在相变过程中,焓变导致曲线剧烈变化,应考虑在较大的温度范围内物流焓值随温度变化的特性,存在相变情况下采用分段函数关系式。如图 2所示。
|
图 2 相变过程中焓值温度关系 Fig.2 Enthalpy profiles as a function of temperature in phase changing processes |
为表征塔压变化后物流的真实热性质,作出一系列物流的温度焓值散点数据,拟合出物流焓值和对应温度之间的相互关系。对于存在相变的物流,其焓值温度关系可通过分段函数表示热容流率为非常数的特性:
| $ \left\{ \begin{array}{l} {H_s} = {f_1}\left( T \right) = {\kern 1pt} \sum\limits_{i = 1}^n {{a_{is}}{T^{n - i + 1}} + {b_s}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} T \le TC\\ {H_s} = {f_2}\left( T \right) = {\kern 1pt} \sum\limits_{i = 1}^n {{{a'}_{is}}{T^{n - i + 1}} + {{b'}_s}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} T \ge TC \end{array} \right. $ | (6) |
其中TC为温焓曲线的拐点。在式 (7) 引入布尔变量在模型中实现上述组合计算。式中,mu为极大量正值,w为极小量正值。
| $ \left\{ {\begin{array}{*{20}{c}} {{H_{\rm{s}}} \le {f_1} + {f_2}}\\ {\begin{array}{*{20}{c}} {{f_1}\left( T \right) \le \sum\limits_{i = 1}^n {{a_{i{\rm{s}}}}{T^{n - i + 1}}} + {b_{\rm{s}}}}\\ {{f_2}\left( T \right) \le \sum\limits_{i = 1}^n {{{a'}_{_{i{\rm{s}}}}}{T^{n - i + 1}}} + {{b'}_{\rm{s}}}}\\ {\begin{array}{*{20}{c}} {{Z_1} + {Z_2} = 1}\\ {{f_1}\left( T \right) \le {Z_1}mu}\\ {{f_2}\left( T \right) \le {Z_2}mu}\\ {\begin{array}{*{20}{c}} {w\left( {T - TC} \right) + w \le {Z_1}mu}\\ { - w\left( {T - TC} \right) \le {Z_2}} \end{array}} \end{array}} \end{array}} \end{array}} \right. $ | (7) |
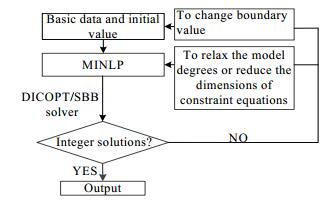
MINLP模型的求解具有复杂性,建议采用罚函数和外逼近法相结合的方法求解MINLP模型。通用代数建模系统 (GAMS) 中开发了DICOPT优化软件包求解MINLP问题。DICOPT给出的求解结果并不能保证一定得到全局最优解,但足以获得满意的换热网络。针对本研究,给出了基于GAMS环境下的求解策略。推荐使用CONOPT、MINOS、SNOPT等优化软件包求解松弛的RMINLP (Relaxed MINLP,RMINLP) 模型。模型采用不同的求解器只为得到可行解。当模型中存在复杂的高阶约束方程,导致模型求解困难或者只能解出局部最优解而非全局最优解,可采用如图 3所示的松弛策略降低约束方程的维度和非线性,迅速找到整数优化解。
|
图 3 可行解求解策略 Fig.3 Flowchart of solving strategy for feasible solutions |
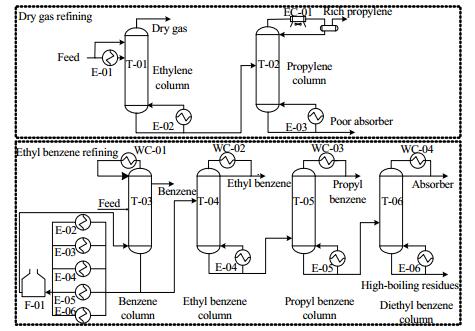
以某炼化企业乙苯装置的精馏系统为研究对象。乙苯产量为20 Mt·a-1,干气、乙苯精制及相应的换热网络如图 4所示。干气精制后经过烃化和反烃化制取芳烃,烃化产物经过粗分,精馏制取乙苯。
|
图 4 干气和乙苯精制的精馏系统 Fig.4 Schematic diagram of a distillation system for dry gas and ethyl benzene refining processes |
考虑到苯塔和乙苯塔以加热炉为热源,故忽略两塔压力变化对塔底再沸器换热面积的影响。故目标函数简化为:
| $ $\begin{array}{l} {\rm{min }}Obj{\rm{ }} = \left[{h\left( {\sum\limits_{i \in HP} {CCUqc{u_i} + \eta \sum\limits_{j \in CP} {CHUqh{u_j}} } } \right)} \right] + \\ \frac{{\sum\limits_{{\rm{i}} \in {\rm{HP}}} {\sum\limits_{j \in CP} {\sum\limits_{k \in ST} {C{F_{i, j}}{Z_{i, j, k}}} + \sum\limits_{i \in HP} {\sum\limits_{j \in CP} {\sum\limits_{k \in ST} {\left\{ {{C_{i, j}}{{\left[{{q_{i, j, k}}/\left( {{U_{i, j}}LMT{D_{i, j, k}}} \right)} \right]}^{{B_{ij}}}}} \right\}} } } } } }}{{pt}}\\ + \frac{{\sum\limits_{i \in HP} {C{F_{i, CU}}{Z_{CU, i}}} + \sum\limits_{i \in HP} {\left\{ {{C_{i, CU}}{{\left[{qc{u_i}/\left( {{U_{i, CU}}LMT{D_{i, CU}}} \right)} \right]}^{{B_{i, CU}}}}} \right\}} }}{{pt}} \end{array}$ $ | (8) |
各塔的关键操作参数见表 1。
| 表 1 模拟中各塔关键参数 Table 1 Key parameters of columns used in simulation |
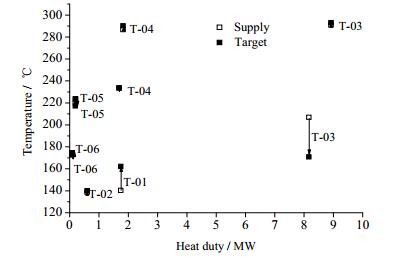
依据模拟数据做出如图 5所示的温焓图,其中箭头朝上为冷物流,箭头朝下为热物流。直观判断换热网络设计中可能存在热交换的流股。为减少换热网络模型的求解规模,给出以下快速辨识热集成物流的判据:(1) 热物流温度高于冷物流温度 (箭头朝下的物流应在箭头朝上的物流上方);(2) 避免使用热公用工程 (加热费用高),即热物流的热负荷高于冷物流 (箭头朝下的物流应该在箭头朝上的物流的右方)。
|
图 5 塔间热集成物流的温位与热负荷 Fig.5 Relationship between temperature and heat duty for heat integration streams of different columns |
根据以上启发式换热规则,选取T-01和T-02的再沸物流、T-03和T-04的冷凝物流进行热集成。建立图 1所示的分级超结构。
4.2 塔压及温焓关联方程优化模型需关联塔压变量及温度变量。受限于苯塔加热炉设计负荷影响,在集成过程中再沸负荷应变化较小,故模拟时保持回流比不变。采用灵敏度分析分别考察苯塔和乙苯塔塔顶蒸汽温度与塔压的关系。利用最小二乘法拟合多项式约束方程,见式 (9) 和 (10)。
| $ TI{N_1} = 2.270P_1^3- 21.538P_1^2 + 88.099{P_1} + 108.3\begin{array}{*{20}{c}} {}&{\left( {{\rm{R}^2} = 0.999, {P_1} \in \left[{1.5, 1.7} \right]{\rm{ }}} \right)} \end{array} $ | (9) |
| $ TI{N_2} = 31.245P_2^3- 109.84P_2^2 + 190.33{P_2} + 135.78\begin{array}{*{20}{c}} {}&{\left( {{\rm{R}^2} = 0.998, {P_2} \in \left[{0.6, 0.9} \right]{\rm{ }}} \right)} \end{array} $ | (10) |
上式PUpper为稳态的上限值,PLower为给定的下限值。将P的范围转换为TIN的边界:
| $ {\left( {TI{N_i}} \right)_{{\rm{Lower}}}} \le TI{N_i} \le {\left( {TI{N_i}} \right)_{{\rm{Upper}}}} $ | (11) |
在塔压变化下,苯塔及乙苯塔塔顶回流温度随进塔温度呈定量关系,见式 (12) 和 (13)。
| $ TOU{T_1} = 0.4628TI{N_1} + 75.368\begin{array}{*{20}{c}} {}&{\left( {{\rm{R}^2} = 0.999} \right)} \end{array} $ | (12) |
| $ TOU{T_2} = 1.004TI{N_2}-0.1353\begin{array}{*{20}{c}} {}&{\left( {{\rm{R}^2} = 0.989} \right)} \end{array} $ | (13) |
苯塔全塔平均压力为1.6 MPa,塔顶蒸汽流量为81453 kg·h-1。乙苯塔全塔平均压力为0.75 MPa,塔顶塔塔顶蒸汽流量为27567 kg·h-1。苯塔顶气的相变温度点为TC1 = 203.5℃;乙苯塔顶蒸汽在0.75 MPa压力,温度范围为185~237℃时无明显相变过程。拟合得到的苯塔及乙苯塔塔顶物流焓值与温度的多项式关系见式 (14) 和 (15)。
| $ \left\{ \begin{array}{c} H = 3 \times {10^{-5}}{T^4}-0.0194{T^3} + 5.2618{T^2}\begin{array}{*{20}{c}} {-634.25T + 28661\begin{array}{*{20}{c}} {}&{T \le TC} \end{array}}&{}&{} \end{array}\\ H = 0.0435T + 17.98\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{T \ge TC} \end{array} \end{array} \right. $ | (14) |
| $ H = 0.0191T-1.9492 $ | (15) |
脱乙烯塔塔底再沸物流的相变温度点为TC1 = 172.0℃,脱丙烯塔塔底再沸物流的相变温度点为TC2, 2 = 142.8℃,脱丙烯塔的焓值曲线在TC2, 1 = 138.8℃,存在拐点,为更好反映实际物流的温焓关系,分三段利用最小二乘法拟合多项式,分别见式 (16) 和 (17)。
| $ \left\{ \begin{array}{l} H = 0.0000257{T^4}-0.01459{T^3} + 3.4975{T^2}-341.67T + 13694.4\begin{array}{*{20}{c}} {}&{}&{T \ge TC} \end{array}\\ H = 0.02994T + 0.0141\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{T \le TC} \end{array} \end{array} \right. $ | (16) |
| $ \left\{ \begin{array}{l} H = 0.0337T + 7.5928\begin{array}{*{20}{c}} {}&{}&{T \le T{C_{2, 1}}} \end{array}\\ H = 0.144{T^3}-62.778{T^2} + 7861.11T-469444\begin{array}{*{20}{c}} {}&{T{C_{2, 1}} \le T \le T{C_{2, 2}}} \end{array}\\ H = 0.0248T + 14.3299\begin{array}{*{20}{c}} {}&{}&{T \ge T{C_{2, 2}}} \end{array} \end{array} \right. $ | (17) |
冷物流进出口温度固定,TCIN1 = 140.4℃;TCIN2 = 138.79℃;TCOUT1 = 168.34℃;TCOUT2 = 140.19℃。得到两条冷物流焓变负荷Ech1 = 1.740 MW;Ech2 = 0.597 MW。同时规定如下参数[14]:h = 8400 h;pt = 1;ε = 10℃;TINCU = 20℃;TOUTCU = 30℃;加热蒸汽选择1.0 MPa蒸汽 (TINHU = 179℃,TOUTHU = 175℃);所有物流的膜传热系数设定为0.0001 MW·(m2·℃)-1。CCU=5×10-7 CNY·MJ-1,CHU=1.53×10-5 CNY·MJ-1。
换热器设备费用:
| $ {\rm{COST}} = CF + C \cdot {\left( {Area} \right)^B} $ | (18) |
式中CF为固定费用,5500 CNY;B为面积费用因子,1;C为换热器的费用系数,3000 CNY·m-2。
4.3 计算结果与讨论定义以下两种状态:状态1为耦合塔压变量的热集成优化模型;状态2为无热集成,全部采用公用工程。
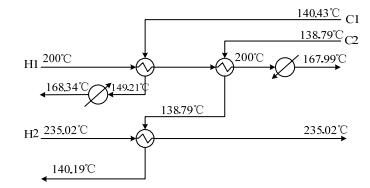
DICOPT求解器难以得到整数解,由GAMS23.0中SBB求解器求解状态1,在计算硬件环境下 (Windows 10,Core i5-4210M,2.60 GHz,RAM 12.00 GB) 总共耗时0.016 s,TAC为9310000 CNY·a-1,详细计算结果见表 2。换热网络结构如图 6所示。
| 表 2 状态1模型计算结果 Table 2 Simulation results of scenario 1 |
|
图 6 热集成的换热网络 Fig.6 Heat exchanger network of the heat integration system |
状态2的苯塔压P1 = 1.6 MPa,乙苯塔塔压P2 = 0.6 MPa,选取的冷物流进出口温度,膜传热系数等参数与状态1相同。TAC为49200000 CNY·a-1,计算结果见表 3。
| 表 3 状态2模型计算结果 Table 3 Simulation results of scenario 2 |
塔压变量优化的TAC更小,经济效益为39890000 CNY·a-1。热集成的换热结构中,换热器增加到五个,其中工艺物流之间的换热器为三个,与公用工程之间的换热器为两个。H2和C2两股工艺物流经过流股之间热交换后能够完全达到目标温度,无需公用工程。热集成后的换热总面积约为2826 m2,而状态2的换热总面积达8343 m2,热集成通过工艺物流间换热大大减少换热面积。
热集成后的公用工程费用约为3630000 CNY·a-1,而全部采取公用工程时的费用为12070000 CNY·a-1,热集成可节省公用工程费用节省8440000 CNY·a-1。工艺物流之间热交换量越多,公用工程费用越低。进行热集成的另一重要效益来源是换热器的面积投资费用,塔间热集成可大大减小公用工程换热面积,从而减少换热器投资。
对单个冷热物流换热而言,热物流压力越高,温度越高,传热温差越大,面积小,投资越小,压力越高越合适。但通过本案例研究发现,在有多条冷热物流的换热网络中,并非所有的热物流温度越高越好,因为所有热物流压力升高导致温度升高可能会产生与冷物流换热的竞争,反而排除了最优换热网络结构和参数。因此,在压力参数作为塔间热集成的关键耦合参数时,并非尽可能增加所有塔 (热源) 的操作压力。
5 结论论文给出了耦合塔压变量的精馏系统塔间热集成的优化策略及模型。给出了热集成物流筛选的启发式规则,并以年度总费用为目标函数建立了考虑塔压参数作为变量的热集成优化模型,考虑到塔间热集成中,再沸器及冷凝器物料存在相变,引入二元变量,提出存在相变的物流焓值分段计算方法。案例结果表明相比不采用热集成的方案,塔压及换热网络同时优化的方案经济效益更优。
优化结果显示塔压并不是越高越好。在有多条冷热物流的换热网络中,并非所有的热物流温度越高越好。因为不同热物流压力升高导致温度升高可能会产生与冷物流换热的竞争,反而排除了最优换热网络结构和参数。因此,在压力参数作为塔间热集成的关键耦合参数时,并非尽可能增加所有塔 (热源) 的操作压力,不应忽视换热网络对塔参数的反向作用及影响。
| 符号说明: | |||
| a | ——多项式拟合系数 | TC | ——相变温度 |
| b | ——多项式的常数项 | TCIN | ——再沸物流相变前温度,℃ |
| B | ——面积费用因子 | TCOUT | ——再沸物流相变后温度,℃ |
| C | ——面积费用系数,CNY·m-2 | TIN | ——物流进口温度,℃ |
| CF | ——换热器的固定费用,CNY | TOUT | ——物流的出口温度,℃ |
| CU | ——冷公用工程 | Z1, Z2 | ——分段方程选择变量 |
| CCU | ——单位热量的冷公用工程费用,CNY·(W∙h)-1 | ZCU, i | ——冷公用工程与热物流i是否换热 |
| CHU | ——单位热量的热公用工程费用,CNY·(W∙h)-1 | Zi, j, k | ——换热级上是否存在换热匹配 |
| dti, j, k | ——温度点k换热匹配 (i,j) 的温差,℃ | w | ——极小的正数 |
| Ech | ——物流焓变负荷,MW | ε | ——最小传热温差,℃ |
| h | ——年操作时间,h | η | ——加热炉效率 |
| HU | ——热公用工程 | Γ | ——温差上限,℃ |
| LMTD | ——传热温差,℃ | Ω | ——换热上限,℃ |
| mu | ——极大的正数 | CP | ——冷物流集合 |
| Nc | ——冷物流的数目 | HP | ——热物流集合 |
| Nk | ——换热的级数 | ST | ——工艺物流间换热集合 |
| Nh | ——热物流的数目 | 下标 | |
| NOK | ——换热级数 | b | ——函数分段 |
| pt | ——回收期 | i | ——冷物流 |
| qi, j, k | ——换热级上热物流i和冷物流j的换热量,W | j | ——热物流 |
| qcui | ——热物流和冷公用工程的换热量,W | k | ——换热级 |
| qhuj | ——冷物流和热公用工程的换热量,W | Lower | ——下限 |
| ti, k | ——换热级上热端热物流i的温度,℃ | s | ——物流 |
| tj, k | ——换热级上冷端冷物流j的温度,℃ | Upper | ——上限 |
| [1] | KANG Li-xia(康丽霞), JIANG Nan(姜楠), XIA Ming-xing(夏明星), et al. Parallel genetic algorithm for design of HEN based on OpenMP system(基于OpenMP的并行GA加速求解换热网络设计)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2016, 30(2): 431-438. |
| [2] | WEI Ying(魏颖), FENG Xiao(冯霄). Research and progress on heat integrated complex system synthesis(塔系热集成问题的研究及进展)[J]. Petroleum & Chemical Energy Conservation(石油和化工节能) , 2007(5): 3-5. |
| [3] | ZHAN Shi-hui(湛世辉), WANG Yu-fei(王彧斐), FENG Xiao(冯霄). Heat integration of columns in styrene plant(苯乙烯装置塔系热集成)[J]. Chemical Industry and Engineering Progress(化工进展) , 2015, 34(6): 1564-1568. |
| [4] | LI Chun-yan(李春妍), ZHANG Lü-hong(张吕鸿), PAN Xu-ming(潘旭明). Application of differential pressure thermally coupled distillation technology in high-purity pentane(差压热集成技术在高纯戊烷生产中的应用)[J]. Acta Petrolei Sinica (Petroleum Processing Section)(石油学报 (石油加工)) , 2011, 27(2): 308-312. |
| [5] | Aly S. Heuristic approach for the synthesis of heat integrated distillation sequences[J]. International Journal of Energy Research , 1997, 21(14): 1297-1304. DOI:10.1002/(ISSN)1099-114X. |
| [6] | WANG Xu(汪旭), FENG Xiao(冯霄). Heat integration of distillation system based on simulation analysis and heuristic approach(基于模拟分析技术和启发式方法的精馏塔系热集成)[J]. Journal of North China Electric Power University(华北电力大学学报) , 2010, 37(1): 87-91. |
| [7] | QIAN Xin-hua(钱新华), SUN Xiao-jing(孙晓静), WANG Ke-feng(王克峰), et al. Energy integration based on simulation analysis and stochastic search(基于模拟分析技术和随机搜索算法的化工过程能量集成方法研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2007, 21(2): 322-327. |
| [8] | SUN Yan-ze(孙艳泽), FENG Xiao(冯霄). Heat integration of equipments with different operating conditions(具有不同操作工况的装置的热集成)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2007, 21(5): 843-848. |
| [9] | LI Yu-gang(李玉刚), LI Chun-xin(李春欣), ZHANG Wei(张伟), et al. Heat integration of separation process for mixture with wide boiling-range(宽沸程物系分离过程的热集成)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2008, 22(1): 34-37. |
| [10] | WU Meng-bing(吴孟兵). Heat integration distillation process in the application of pentane plant(热集成精馏工艺在戊烷装置中的应用)[J]. Chemical Engineering & Equipment(化学工程与装备) , 2016(1): 17-19. |
| [11] | HAN Zhen(韩祯), LI Hong-da(李宏达), GAO Xin(高鑫), et al. Process simulation of separation of isopropylacetate-isopropanol mixture by pressure swing distillation with heat integration(乙酸异丙酯-异丙醇物系的热集成变压精馏分离模拟)[J]. Petrochemical Technology(石油化工) , 2015, 44(6): 663-668. |
| [12] | Andrecovich M J, Westerberg A W. An MILP formulation for heat integrated distillation sequence synthesis[J]. AIChE Journal , 1985, 31(9): 1461-1474. DOI:10.1002/(ISSN)1547-5905. |
| [13] | WANG Ke-feng(王克峰), YIN Hong-chao(尹洪超), YAO Ping-jing(姚平经), et al. Simultaneous optimization for separation system and heat exchanger network using genetic algorithm and neural network(分离系统与换热网络同步优化方法的改进神经元网络-遗传算法)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 1997, 11(3): 294-299. |
| [14] | Lei Y, Qi X, Zhang B J, et al. Simultaneous optimization of the complex fractionator and heat exchanger network considering the constraints of variable heat removals in delayed coking units[J]. Industrial & Engineering Chemistry Research , 2014, 53(33): 13073-13086. |
| [15] | Yee T F, Grossmann I E. Simultaneous optimization models for heat integration-Ⅱ. Heat exchanger network synthesis[J]. Computers & Chemical Engineering , 1990, 14(10): 1165-1184. |




