甲基丙烯酸甲酯本体聚合动力学模型

引用本文

汪情兵, 张才亮, 冯连芳, 顾雪萍, 王嘉骏. 甲基丙烯酸甲酯本体聚合动力学模型[J]. 高校化学工程学报, 2018, 32(5): 1097-1103. DOI: 10.3969/j.issn.1003-9015.2018.05.014.

WANG Qing-bing, ZHANG Cai-liang, FENG Lian-fang, GU Xue-ping, WANG Jia-Jun. Kinetic Modeling of Methyl Methacrylate Bulk Polymerization[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(5): 1097-1103. DOI: 10.3969/j.issn.1003-9015.2018.05.014.

基金项目

国家重点研发计划（2017YFE0106700）；中央高校基本科研业务费专项资金（2017FZA4024）。

通讯联系人

顾雪萍, E-mail: guxueping@zju.edu.cn

作者简介

汪情兵(1992-), 男, 安徽安庆人, 浙江大学硕士生。

文章历史

收稿日期：2018-01-31;
修订日期：2018-04-19。

Contents Abstract Full text Figures/Tables PDF

甲基丙烯酸甲酯本体聚合动力学模型

汪情兵 , 张才亮 , 冯连芳 , 顾雪萍 , 王嘉骏

化学工程联合国家重点实验室 (浙江大学)，浙江大学化学工程与生物工程学院，浙江杭州 310027

收稿日期：2018-01-31；修订日期：2018-04-19。

基金项目：国家重点研发计划（2017YFE0106700）；中央高校基本科研业务费专项资金（2017FZA4024）。

作者简介：汪情兵(1992-), 男, 安徽安庆人, 浙江大学硕士生。

通讯联系人：顾雪萍, E-mail: guxueping@zju.edu.cn

摘要：甲基丙烯酸甲酯本体聚合动力学研究可指导聚甲基丙烯酸甲酯的聚合工艺和反应器设计。甲基丙烯酸甲酯本体聚合过程凝胶效应显著，基于扩散理论，结合分子量、聚合物浓度对黏度的影响规律，同时考虑玻璃化温度，建立了凝胶效应框架模型。通过在玻璃化温度上/下甲基丙烯酸甲酯间歇聚合实验数据，确定模型参数。聚合过程的单体转化率计算值与实验数据吻合，聚合物数均分子量的计算误差在±7%内。该模型可应用于含有引发剂和链转移剂、在玻璃化温度上/下聚合的甲基丙烯酸甲酯体系。

关键词：凝胶效应甲基丙烯酸甲酯本体聚合玻璃化温度

Kinetic Modeling of Methyl Methacrylate Bulk Polymerization

WANG Qing-bing, ZHANG Cai-liang, FENG Lian-fang, GU Xue-ping, WANG Jia-Jun

State Key Laboratory of Chemical Engineering, College of Chemical and Biological Engineering, Zhejiang University, Hangzhou 310027, China

Abstract: Study of methyl methacrylate bulk polymerization kinetics is beneficial to the understanding of polymerization process and reactor design. Gel effect is an important factor in methyl methacrylate bulk free radical polymerization. Solution viscosity is related to concentration, temperature, molecular weight distribution and glass transition temperature of the polymer. Mathematical framework of gel effect in radical polymerization was developed based on diffusion theory to describe methyl methacrylate bulk polymerization processes. Parameters of the gel effect model were determined by experiment data at temperature lower and higher than the glass transition temperature. The calculated conversion results were in good agreement with the data measured from experiments. The calculated relative deviation of number-average molecular weight was less than 7%. The model is suitable for methyl methacrylate bulk polymerization with initiators and chain transfer agents.

Key words: gel effect methyl methacrylate bulk polymerization glass transition temperature

1 前言

聚甲基丙烯酸甲酯(PMMA)模塑料以热成型、注塑为主，广泛应用于光学材料和玻璃替代品，主要生产工艺为低温溶液聚合和高温本体聚合。甲基丙烯酸甲酯(MMA)自由基本体聚合过程中，凝胶效应现象尤为显著，高转化率下的凝胶效应不可避免^[1-2]。对聚合过程全程动力学的准确理解可指导生产工艺流程的设计和工艺条件的优化。

在众多研究MMA聚合的凝胶效应模型中，可以分为两类：低于玻璃化温度的低温聚合和高于玻璃化温度的高温聚合。

针对MMA低于玻璃化温度的聚合过程，Cardenas^[3]建立了凝胶效应数学模型，认为链终止反应速率常数k_t主要取决于聚合物体系的缠结密度以及聚合度。North^[4]提出聚合终止反应是活性自由基链节扩散控制而不是活性自由基中心的平移扩散控制。Marten^[5]提出k_t与分子量、自由体积有关。以上模型的不足之处在于模型中凝胶效应临界点^[6]的引入使得模型方程不具备连续性。为了避免引入凝胶点而导致数学模型不连续的缺陷，Soong^[7]提出了经典的CCS数学模型，认为转化率的突然增大是自由基扩散速率下降的结果，k_t由本征终止反应速率常数和扩散传质因子两部分构成，但模型将分子量对k_t的影响仅仅与引发剂初始浓度关联，只适用于仅含有引发剂而不存在链转移剂的聚合体系。在CCS模型理论基础上，Achilias^[8]将20个以上的传质参数赋予物理意义，当聚合体系变得复杂，模型参数将会更多，且文献中报道的相关参数只能应用于50~90℃的聚合体系，一定程度上限制了其应用。Tefera^[9]基于三段控制理论：聚合初期的链节扩散，聚合中期的平移扩散，聚合后期的反应扩散，以MMA本体聚合实验数据拟合得到半经验数学模型。蒋晓磊^[10]在此基础上提出了改进的黏度模型，但只应用于含有引发剂、链转移剂且低于玻璃化温度聚合的体系。

针对高于玻璃化温度的MMA聚合过程，Fleury^[11]以CCS低温模型为基础，提出了高温条件(135~165℃)下的凝胶效应模型，但模型仅适用于一定的引发剂浓度范围，当存在链转移剂的条件下，模型不适用。Fenouillot^[12]弥补Fleury的缺陷，将链转移剂初始浓度关联到数学模型中，但其参数仅关联反应温度和链转移剂初始浓度，当体系中引发剂浓度改变时模型不适用，且上述模型仅仅应用于高于玻璃化温度的聚合体系。

针对上述低于玻璃化温度和高于玻璃化温度凝胶效应模型存在的局限性，在扩散控制理论的基础上，考虑分子量及其分布、温度等对黏度的影响，提出基于分子量及其分布、温度以及玻璃化温度的凝胶效应框架模型。

2 MMA本体聚合实验

PMMA的玻璃化温度(T_g)为114℃^[7]。聚合温度低于T_g的MMA本体聚合实验在不锈钢封管中进行，反应温度分别为50、70、90℃，引发剂为偶氮二异丁腈(AIBN)，浓度分别为15.48、25.80 mmol·L^-1，单体转化率由溶解沉降法得到。

聚合温度高于T_g时，MMA在德国耐驰公司DSC 204HP型的差式扫描量热仪中等温聚合，反应温度分别为120、132、150℃，引发剂为过氧化二叔丁基(DTBP)，链转移剂为1-丁硫醇。称取单体、引发剂、链转移剂的混合溶液约50 mg，注入高压密封盘，设定测试程序，在线测量整个聚合过程的放热情况，得到转化率曲线。

PMMA分子量及其分布通过凝胶渗透色谱分析仪得到。仪器为美国Waters公司的Waters 1525/2414凝胶渗透色谱仪。洗脱温度为30℃，流动相为四氢呋喃，流速为1 mL·min^-1，标样为Varian公司的PMMA，色谱柱：PLgel 10 μm 500A 300 mm×7.5 mm、PLgel 10 μm 10E3A 300 mm×7.5 mm、PLgel 10 μm 10E4A 300 mm×7.5 mm。

3 MMA本体聚合模型的建立 3.1 MMA聚合反应机理

MMA聚合反应属于自由基聚合，其基元反应和相应的速率常数表达式如表 1所示，其中，I为引发剂，M为单体MMA，P_n为聚合度为n的死聚体，P_n▪为聚合度为n的活聚体，CTA为链转移剂。反应动力学常数如表 2所示。

表 1 MMA本体聚合机理 Table 1 MMA bulk polymerization mechanism

表 2 MMA本体聚合动力学数据 Table 2 Kinetic data for MMA bulk polymerization

3.2 凝胶效应模型

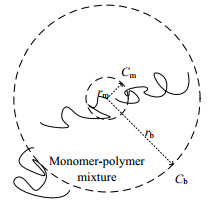
假设整个聚合反应过程由扩散控制，终止反应过程如图 1所示，当两个自由基的平均距离小于r_m时，反应速率为此条件下的本征速率k_t0，k_p0。当r≥r_b时，自由基浓度不受凝胶效应影响，为原始浓度C_b。J是自由基进入半径r_m圆球内的净平均质量通量，费克第一定律在球坐标的稳态解为：

$ J = 4\pi {r^2}D\frac{{{\rm{d}}C}}{{{\rm{d}}r}} $

(1)

图 1 自由基聚合扩散控制链终止示意图 Fig.1 Schematic diagram of free radical termination under diffusion control

边界条件：

$ \begin{array}{l} C = {C_{\rm{m}}}, r = {r_{\rm{m}}}\\ C = {C_{\rm{b}}}, r = {r_{\rm{b}}} \end{array} $

(2)

球面模型假设：自由基由本体进入球内的速率与自由基消耗速率相等(假设在球形内，终止速率并不是扩散控制，而是本征终止)。动力学平衡公式如下：

$ {\rm{4}}\pi {r_{\rm{m}}} \cdot {D_{{\rm{eff}}}} \cdot \left( {{C_{\rm{b}}} - {C_{\rm{m}}}} \right){\rm{ = }}\frac{{\rm{4}}}{{\rm{3}}}\pi {r_{\rm{m}}}^3 \cdot {k_{{\rm{t, 0}}}} \cdot {C_{\rm{b}}} \cdot {C_{\rm{m}}} $

(3)

表观终止速率可表示为k_t×C_b×C_b，等于k_t0×C_m×C_b。即：

$ {k_{\rm{t}}} \cdot C_{\rm{b}}^2{\rm{ = }}{k_{{\rm{t0}}}} \cdot {C_{\rm{b}}} \cdot {C_{\rm{m}}} $

(4)

联立式(3)、(4)，表观终止速率常数=本征终止速率常数+扩散影响，即：

$ \frac{1}{{{k_{\rm{t}}}}} = \frac{1}{{{k_{{\rm{t, 0}}}}}} + \frac{{r_{\rm{m}}^2 \cdot {C_{\rm{b}}}}}{{3{D_{{\rm{eff}}}}}} $

(5)

r_m为定值，聚合物分子量M_w与初始引发自由基浓度C_b有关。

对于MMA本体自由基聚合反应，链终止反应速率常数k_t不但与聚合体系内PMMA活性自由基线团卷曲程度及密度有关，更与PMMA活性自由基链段的运动能力有关，而PMMA活性自由基链段的运动能力一方面取决于聚合温度，另一方面取决于聚合体系的玻璃化温度T_g(体系)。T_g(体系)不仅由PMMA的玻璃化温度决定，还会受到MMA溶剂化的影响，因此扩散系数D_eff不仅仅受转化率的影响，同时还受到聚合反应温度、分子量及其分布的影响，则式(5)右边第二项由转化率项f_t1(x)、聚合温度项f_t2(T)、分子量及其分布项f_t3(M_w, PDI)组成，即：

$ \frac{{r_{\rm{m}}^2{C_{\rm{b}}}}}{{3{D_{{\rm{eff}}}}}} = {f_{{\rm{t1}}}}(x) \cdot {f_{{\rm{t2}}}}(T) \cdot {f_{{\rm{t3}}}}({M_{\rm{w}}}, {\rm{PDI}}) $

(6)

单体MMA溶剂化对T_g(体系)的影响与转化率的影响是协同的，一并考虑在f_t1(x)中。基于自由体积理论^[16]，转化率对扩散系数D_eff的影响，引入Fujita-Doolittle公式，则：

$ {\rm{log}}\frac{{{f_{{\rm{t1}}}}(x)}}{{{f_{{\rm{t1}}}}(0)}} = \frac{{{\phi _{\rm{m}}}}}{{A + B \cdot {\phi _{\rm{m}}}}};{\phi _{\rm{m}}} = \frac{{1 - x}}{{1 + \varepsilon x}} $

(7)

f_t1 (0)是转化率为0时的扩散系数，参数ε为体积收缩因子，A和B由文献[7]得到：

$ \begin{array}{l} A = 0.168 - 8.21 \times {10^{ - 6}}{(T - {T_{\rm{g}}})^2}\\ B = 0.03 \end{array} $

(8)

宏观上，凝胶效应由体系黏度的突然增大而引起。聚合反应温度、分子量及其分布对扩散系数的影响可引入特性黏度表达式(9)，f_t3(M_w, PDI)仅与聚合物的链结构有关，将黏度参数α与聚合物的T_g(PMMA)相关联。

$ \begin{array}{l} [\eta ] = {k_\eta }M_\eta ^\alpha \\ {M_\eta } = {M_{\rm{w}}} \cdot {({\rm{PDI}})^{(\alpha - 1)/2}}\\ \alpha = f(T, {T_{\rm{g}}}) \end{array} $

(9)

联立以上方程，可得到表观终止速率常数：

$ \frac{1}{{{k_{\rm{t}}}}} = \frac{1}{{{k_{{\rm{t, 0}}}}}} + {f_{\rm{t}}}(T)\frac{{{{(M_{\rm{w}}^\alpha \times {\rm{PD}}{{\rm{I}}^{\alpha \times (\alpha - 1)/2}})}^\beta }}}{{{\rm{exp}}\left( {\frac{{2.3(1 - x)/(1 + \varepsilon \cdot x)}}{{A + B(1 - x)/(1 + \varepsilon \cdot x)}}} \right)}} $

(10)

同理，链增长是长链自由基与小分子单体自由基的反应，在反应后期，同样受扩散控制，此时扩散因子可与转化率、聚合温度关联，即表观链增长速率常数：

$ \frac{1}{{{k_{\rm{p}}}}} = \frac{1}{{{k_{{\rm{p, 0}}}}}} + {f_{\rm{p}}}(T)\frac{{{C_{\rm{b}}}}}{{{\rm{exp}}\left( {\frac{{2.3(1 - x)/(1 + \varepsilon \cdot x)}}{{A + B(1 - x)/(1 + \varepsilon \cdot x)}}} \right)}} $

(11)

3.3 转化率及分子量分布计算

为了计算MMA本体聚合的单体转化率和分子量及其分布，采用矩方法(moment method^[17])，如表 3所示，建立聚合体系物料衡算方程，求解微分方程组并拟合参数。由在玻璃化温度上下MMA本体聚合实验数据，得到凝胶效应模型的参数如下：

$ \begin{array}{l} {f_{\rm{t}}}(T) = 2.5 \times {10^{ - 11}}{\rm{exp}}(187.8/T)\\ {f_{\rm{p}}}(T) = 2.3 \times {10^{ - 16}}{\rm{exp}}(14192.9/T)\\ \alpha = \left\{ \begin{array}{l} 0.56 + 0.6 \times ({T_{\rm{g}}} - T)/{T_{\rm{g}}}{\rm{ }}(T < {T_{\rm{g}}})\\ 0.56(T > {T_{\rm{g}}}) \end{array} \right\}\\ \beta = 1.60 \end{array} $

(12)

表 3 MMA本体聚合物料守恒方程 Table 3 Mass balance equations of MMA bulk polymerization

$ \frac{{{\rm{d}}[{\rm{I}}]}}{{{\rm{d}}t}} = - {k_{\rm{d}}}[{\rm{I}}] - [{\rm{I}}]\frac{1}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}} $

$ \begin{array}{l} \frac{{{\rm{d}}[{\rm{M}}]}}{{{\rm{d}}t}} = - {k_{\rm{p}}}[{\rm{M}}]{\lambda _0} - {k_{{\rm{trm}}}}[{\rm{M}}]{\lambda _0} + {k_{{\rm{dp}}}}{\lambda _0} - M\frac{1}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}\\ \frac{{{\rm{d}}[{\rm{CTA}}]}}{{{\rm{d}}t}} = - {k_{{\rm{trt}}}}[{\rm{CTA}}]{\lambda _0} - {k_{{\rm{dt}}}}[{\rm{CTA}}] - [{\rm{CTA}}]\frac{1}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}\\ \frac{{{\rm{d}}{\lambda _0}}}{{{\rm{d}}t}} = 2f{k_{\rm{d}}}[I] + {k_{{\rm{dt}}}}[{\rm{CTA}}] + {k_{{\rm{th}}}}{[{\rm{M}}]^2} - {k_{\rm{t}}}{\lambda _0}^2 - \frac{{{\lambda _0}}}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}\\ \frac{{{\rm{d}}{\lambda _1}}}{{{\rm{d}}t}} = 2f{k_{\rm{d}}}[{\rm{I}}] + {k_{{\rm{dt}}}}[{\rm{CTA}}] + {k_{{\rm{th}}}}{[{\rm{M}}]^2} + {k_{\rm{p}}}[{\rm{M}}]{\lambda _0} - {k_{{\rm{dp}}}}{\lambda _0} + ({k_{{\rm{trm}}}}[{\rm{M}}] + {k_{{\rm{trt}}}}[{\rm{CTA}}])({\lambda _0} - {\lambda _1}) - {k_{\rm{t}}}{\lambda _0}{\lambda _1} - \frac{{{\lambda _1}}}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}\\ \frac{{{\rm{d}}{\lambda _2}}}{{{\rm{d}}t}} = 2f{k_{\rm{d}}}[{\rm{I}}] + {k_{{\rm{dt}}}}[{\rm{CTA}}] + {k_{{\rm{th}}}}{[{\rm{M}}]^2} + ({k_{\rm{p}}}[{\rm{M}}] - {k_{{\rm{dp}}}})(2{\lambda _1} + {\lambda _0}) + ({k_{{\rm{trm}}}}[{\rm{M}}] + {k_{{\rm{trt}}}}[{\rm{CTA}}]({\lambda _0} - {\lambda _2}) - {k_t}{\lambda _0}{\lambda _2} - \frac{{{\lambda _2}}}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}\\ \frac{{{\rm{d}}{u_0}}}{{{\rm{d}}t}} = ({k_{{\rm{td}}}} + 0.5{k_{{\rm{tc}}}}){\lambda _0}^2 + ({k_{{\rm{trm}}}}[{\rm{M}}] + {k_{{\rm{trt}}}}[{\rm{CTA}}]{\lambda _0} - \frac{{{u_0}}}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}\\ \frac{{{\rm{d}}{u_1}}}{{{\rm{d}}t}} = {k_t}{\lambda _0}{\lambda _1} + ({k_{{\rm{trm}}}}[{\rm{M}}] + {k_{{\rm{trt}}}}[{\rm{CTA}}]){\lambda _1} - \frac{{{u_1}}}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}\\ \frac{{{\rm{d}}{u_2}}}{{{\rm{d}}t}} = {k_t}{\lambda _0}{\lambda _2} + {k_{{\rm{tc}}}}{\lambda _1}^2 + ({k_{{\rm{trm}}}}[{\rm{M}}] + {k_{{\rm{trt}}}}[{\rm{CTA}}]){\lambda _2} - \frac{{{u_2}}}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}\\ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = ({k_{\rm{p}}} + {k_{{\rm{trm}}}}){\lambda _0}(1 - x) - \frac{{{k_{{\rm{dp}}}}(1 + \varepsilon x){\lambda _0}}}{{{M_0}}}\\ \frac{1}{V}\frac{{{\rm{d}}V}}{{{\rm{d}}t}} = ({k_{\rm{p}}} + {k_{{\rm{trm}}}})\varepsilon \frac{{1 - x}}{{1 + \varepsilon x}}{\lambda _0} - \frac{{{k_{{\rm{dp}}}}\varepsilon {\lambda _0}}}{{{M_0}}}\\ {M_{\rm{n}}} = {M_{\rm{m}}}\frac{{{\lambda _1} + {u_1}}}{{{\lambda _0} + {u_0}}}\\ {M_{\rm{w}}} = {M_{\rm{m}}}\frac{{{\lambda _2} + {u_2}}}{{{\lambda _1} + {u_1}}}\\ PDI = {M_{\rm{w}}}/{M_{\rm{n}}} \end{array} $

表 3 MMA本体聚合物料守恒方程 Table 3 Mass balance equations of MMA bulk polymerization

4 结果与讨论

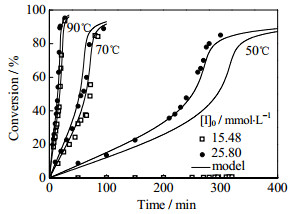
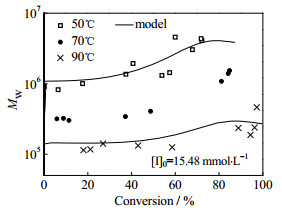
由图 2所示，MMA低于玻璃化温度聚合时，模型计算的单体转化率与实验数据吻合。随着单体转化率提高，聚合体系将依次经历“液态→黏流态→高弹态→玻璃态”。此时，因聚合体系在末期进入玻璃态，聚合反应终止。模型中将黏度参数α与反应温度T、T_g关联，提高聚合反应温度，体系黏度降低，黏度参数α逐渐降低。图 3可见，当引发剂浓度为15.48 mmol·L^-1时，模拟计算的重均分子量随着单体转化率变化曲线与实验数据基本吻合，提高反应温度，聚合速率加快，分子量降低。

图 2 MMA在T_g以下聚合时单体转化率模拟值与实验值比较 Fig.2 Comparison of monomer conversion between model and experimental data for MMA bulk polymerization below T_g

图 3 MMA在T_g以下聚合时重均分子量-转化率模拟值与实验值比较 Fig.3 Comparison of weight-average molecular weight between model and experimental data for MMA bulk polymerization below T_g

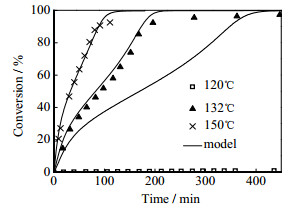
MMA高于玻璃化温度聚合时，由图 4、图 5可以看出，模型能够很好的预测单体转化率随反应时间的变化。当聚合在高于PMMA的玻璃化温度T_g(PMMA)的温度下进行时，聚合过程凝胶效应强度有所减弱，随着单体转化率提高，聚合体系先后将经历“液态→黏流态→高弹态”，无玻璃态。

图 4 MMA在T_g以上聚合时单体转化率模拟值与实验值比较([CTA]0=20.5 mmol·L^-1，[DTBP]₀=0.7 mmol·L^-1) Fig.4 Comparison of monomer conversion between model and experimental data for MMA bulk polymerization above T_g ([CTA]₀=20.5 mmol·L^-1, [DTBP]0=0.7 mmol·L^-1)

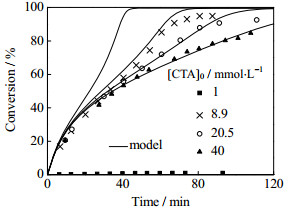
图 5 不同初始链转移剂浓度下MMA在150℃聚合时单体转化率模拟值与实验值比较([DTBP]₀=0.7 mmol·L^-1) Fig.5 Comparison of monomer conversion between model and experimental data for MMA bulk polymerization under different chain transfer agent concentrations at temperature above T_g ([DTBP]₀=0.7 mmol·L^-1)

表 4为模型计算的分子量及其分布与实验值的对比，数均分子量相对误差在±7%以内。随着链转移剂浓度增大，聚合物分子量下降，体系黏度降低，凝胶效应强度也有所减弱，可从图 5单体转化率曲线看出凝胶效应强度随着链转移剂浓度的增大有减弱趋势。

表 4 MMA高温聚合不同条件下分子量及其分布实验数据与模型计算比较 Table 4 Comparison of molecular weight distribution between experimental and model data

5 结论

基于自由基聚合过程的扩散理论，提出了半经验的凝胶效应数学模型。该模型考虑聚合物分子量及其分布、聚合物浓度、反应温度等对聚合体系黏度的影响，并将链终止速率常数、链增长速率常数与其关联。从本体聚合反应机理出发，建立甲基丙烯酸甲酯间歇本体聚合的物料衡算方程，通过反应温度在玻璃化温度上/下的甲基丙烯酸甲酯本体间歇聚合实验数据得到凝胶效应模型的参数，进而预测玻璃化温度上/下的宽温度范围聚合过程的单体转化率及其分子量。分子量计算误差在±7%以内。该模型适用于含有链转移剂和引发剂的聚合体系，为MMA在不同温度下聚合工艺流程及反应器的设计提供指导。

符号说明：

A	—凝胶效应模型参数	k_th	—单体热分解速率常数，(mol·min)^-1
B	—凝胶效应模型参数	k_trm0	—向单体转移初始链转移速率常数，(mol·min)^-1
C_b	—聚合度为n的自由基总浓度，mol·L^-1	k_trm	—向单体转移链转移反应速率常数，(mol·min)^-1
C_m	—两自由基距离r_m时自由基浓度，mol·L^-1	k_trt	—向链转移剂转移链转移速率常数，(mol·min)^-1
[CTA]	—链转移剂浓度，mol·L^-1	[M]	—单体MMA的浓度，mol·L^-1
D_eff	—扩散系数，m²·min^-1	M_n	—质均分子量，g·mol^-1
d_m	—单体MMA的密度，kg·m^-3	M_w	—重均分子量，g·mol^-1
d_p	—聚合物PMMA的密度，kg·m^-3	M_η	—黏均分子量，g·mol^-1
f	—引发剂效率	PDI	—聚合物分子量分布指数
[I]	—引发剂浓度，mol·L^-1	r_m	—球面模型两自由基本征终止反应的距离，m
k_d	—引发剂分解速率常数，min^-1	r_b	—球面模型长链自由基扩散到本征终止区的距离，m
k_dt	—链转移剂分解速率常数，(mol·min)^-1	T	—聚合反应温度，K
k_dp	—聚合物解聚反应速率常数，(mol·min)^-1	V	—聚合体系体积，L
k_p	—表观链增长速率常数，(mol·min)^-1	x	—单体转化率
k_p0	—初始链增长速率常数，(mol·min)^-1	α	—凝胶效应模型黏度参数
k_t	—表观链终止速率常数，(mol·min)^-1	β	—凝胶效应模型黏度参数
k_t0	—初始链终止速率常数，(mol·min)^-1	λ_k	—链增长自由基k(k=0, 1, 2)次矩
k_tc	—偶合链终止速率常数，(mol·min)^-1	μ_k	—死聚物链k(k=0, 1, 2)次矩
k_td	—歧化链终止速率常数，(mol·min)^-1	ε	—体积收缩因子

参考文献

[1]	Norrish R G W, Smith R. Catalyzed polymerization of methyl methacrylate in the liquid phase[J]. Nature, 1942, 150: 336-337. DOI:10.1038/150336a0.
[2]	Ernst T V, Herbert K, Paul L. For the polymerization of meth acrylic acid methyl ester[J]. The Macromolecular Chemistry and Physics, 1948, 1(3): 169-198. DOI:10.1002/macp.1948.020010301.
[3]	Cardenas J N, O'Driscoll K F. High-conversion polymerization. Ⅰ. Theory and application to methyl methacrylate[J]. Journal of Polymer Science Part A Polymer Chemistry, 1976, 14(4): 883-897. DOI:10.1002/pol.1976.170140409.
[4]	North A M, Reed G A. Diffusion-controlled termination during the initial stages of free radical polymerization of methyl methacrylate[J]. Transactions of the Faraday Society, 1961, 57(56): 785-791.
[5]	Marten F L, Hamielec A E. High conversion diffusion-controlled polymerization[J]. ACS Symposium, 1979, 104(10): 43-70.
[6]	Tulig T J, Tirrell M. Molecular theory of the trommsdorff effect[J]. Macromolecules, 1981, 14(5): 1501-1511. DOI:10.1021/ma50006a070.
[7]	Chiu W Y, Carratt G M, Soong D S. A computer model for the gel effect in free-radical polymerization[J]. Macromolecules, 1983, 16(3): 348-357. DOI:10.1021/ma00237a002.
[8]	Achilias D, Kiparissides C. Modeling of diffusion-controlled free-radical polymerization reactions[J]. Journal of Applied Polymer Science, 2010, 35(5): 1303-1323.
[9]	Tefera N, Weickert G, Westerterp K R. Modeling of free radical polymerization up to high conversion. Ⅱ. Development of a mathematical model[J]. Journal of Applied Polymer Science, 1996, 63(12): 1663-1680.
[10]	JIANG Xiao-lei (蒋晓磊). Preparation of poly (methyl methacrylate) with narrow molecular weight distribution by continuous polymerization (窄分子量分布PMMA的连续化制备)[D]. Hangzhou (杭州): Zhejiang University (浙江大学), 2013.
[11]	Fleury P A. Polymerization of methyl methacrylate in high temperature (polymérisation du méthacrylate de méthyle à haute temperature)[D]. Lausanne: Swiss federal Institute of Technology in Lausanne (École Polytechnique Fédérale de Lausanne), 1993.
[12]	Fenouillot F, Terrisse J, Rimlinger T. Polymerization of methyl methacrylate at high temperature with 1-butanethiol as chain transfer agent[J]. Journal of Applied Polymer Science, 1999, 72(12): 1589-1599. DOI:10.1002/(ISSN)1097-4628.
[13]	Ray A B, Saraf D N, Gupta S K. Free radical polymerizations associated with the trommsdorff effect under semi batch reactor conditions. Ⅰ:Modeling[J]. Polymer Engineering & Science, 1995, 35(16): 1290-1299.
[14]	Nising P, Meyer T. Modeling of the high-temperature polymerization of methyl methacrylate. 1. Review of existing models for the description of the gel effect[J]. Industrial & Engineering Chemistry Research, 2004, 43(23): 7220-7226.
[15]	Fenouillot F, Terrisse J, Rimlinger T. Thermal polymerization of methyl methacrylate at high temperature[J]. International Polymer Processing Journal of the Polymer Processing Society, 1998, 13(2): 154-161. DOI:10.3139/217.980154.
[16]	Sharma J, Tewari K, Arya R K. Diffusion in polymeric systems-A review on free volume theory[J]. Progress in Organic Coatings, 2017, 111: 83-92. DOI:10.1016/j.porgcoat.2017.05.004.
[17]	Mastan E, Zhu S. Method of moments:a versatile tool for deterministic modeling of polymerization kinetics[J]. European Polymer Journal, 2015, 68: 139-160. DOI:10.1016/j.eurpolymj.2015.04.018.