2. 西安交通大学 化学工程与技术学院,陕西 西安 710049
2. School of Chemical Engineering and Technology, Xi'an Jiaotong University, Xi'an 710049, China
由于科学技术的飞速发展,现代工业对换热器紧凑性和高效性要求越来越高。采用微通道换热器不仅满足了紧凑性要求,还能利用管内两相流动带来的相变潜热以获得强大的换热能力。此外,它还能减少系统的充灌量,满足节能要求。探索微通道内两相流动的规律对于换热器的设计和优化具有重要意义。目前已有大量的学者对微细通道内冷凝流动特性进行了研究。CAVALLINI等[1]和AWAD等[2]对微细通道内流型、换热系数及压降的实验研究进行了文献综述。大部分研究基本都以氢氟烃作为研究工质,如R134a和R410A。虽然这类工质进入大气后不会对臭氧层造成破坏,但是它们的GWP (global warming potential)高,在大气停留时间长,长期使用会加剧温室效应。可以预见的是,类似于R134a和R410A这类高GWP的含氢氟烃类制冷剂终将会被淘汰。四氟丙烯(R1234ze(E))不仅ODP(ozone depletion potential)为0,GWP值也很低,其物理性能与R134a相似,被认为是未来可替代R134a的新一代制冷剂。MOTA-BABILONI等[3]综述了近年来关于R1234ze(E)的研究进展,发现目前的研究主要围绕其物性、可燃性、与油的相容性以及蒸汽压缩系统的性能展开。关于R1234ze(E)在水平管内的冷凝两相流动的研究很少,且都是采用实验法进行研究。WANG等[4]研究了R1234ze(E)在水力直径为301.6 μm的微通道序列中的流型分布,观察到了环状流、注射流、波状流和泡状流。LIU等[5]研究了丙烷、R1234ze(E)和R22在水平圆管和方管内的冷凝换热系数和压降,发现丙烷和R1234ze(E)换热系数和压降都要大于R22。JIGE等[6]实验研究了R32、R134a、R410A和R1234ze(E)在水平多孔管内的冷凝换热系数及压降,发现R1234ze(E)的压降梯度要大于其他工质。DEL COL等[7]对比了R1234ze(E)、R32、R134a和R1234yf在水平圆管(Dh=1 mm)内的冷凝换热系数及绝热压降梯度。研究发现R1234ze(E)的压降梯度要比R134a和R1234yf大。相同功耗下,R1234ze(E)和R1234yf所需要的换热面积要比R134a分别大25%和15%。HOSSAIN等[8]对比了R1234ze(E)、R32和R410A在水平圆管内的冷凝换热性能,发现R1234ze(E)的换热系数要比R32低20%~45%,但要比R410A高10%~30%。
目前关于R1234ze(E)在微细通道内冷凝流动的研究非常有限,而从制冷剂替代的发展趋势来看,这方面的研究很有必要。现有的研究主要以实验为主,缺乏相应的理论分析。本文通过数值模拟手段,研究了R1234ze(E)在水平管内的冷凝流动,并与R134a进行了对比,讨论了液膜分布规律以及剪切力、重力和表面张力的相对作用,并就现有关联式对R1234ze(E)换热系数和压降的适用性进行了评估和讨论。
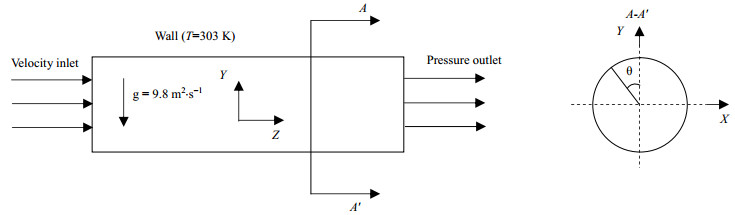
2 数学模型 2.1 计算域如图 1所示,本文采用的几何模型是管径为1 mm的水平微细圆管。管道入口为饱和蒸汽(入口质量流速的变化范围为400~800 kg·m-2·s-1),随着冷凝过程进行,气相减少而液相增多,管内依次会出现雾状流、环状流以及间歇流。本文通过NEMA等[9]提出的流型转化准则来判断流型变化,保证管道的出口干度处于环状流范围,从而确定管长为130 mm。由于本文采用三维稳态模拟,入口段的雾状流假设为环状流。计算域进口为充分发展的速度入口边界条件,出口为压力出口。管壁设定为光滑无滑移且壁面温度为常数(303 K)。工质的物性参数来源于REFPROP 9.0。计算域全部采用六面体网格填充,网格从壁面到管道中心逐渐加密。近壁面网格第一层高度为0.8 μm且Y+小于1。对网格进行无关性验证,当网格数为798万和470万时,换热系数的误差在0.5%以内,因而最终网格数确定在470万左右。
|
图 1 几何示意图及边界条件 Fig.1 Geometric schematic diagram with boundary conditions |
通过求解每一相的体积分数φ,VOF模型可有效追踪互不相混不可压缩流体之间的相界面,现已被成功用于模拟管内的冷凝流动。对于VOF模型,每一个控制体内各项的体积分数之和必须为1。
| $ {{\varphi }_{\text{L}}}+{{\varphi }_{\text{G}}}=1 $ | (1) |
VOF模型将各相混合物看成一种流体,而流动变量和物性参数都取体积平均值
| $ \rho ={{\rho }_{\text{L}}}{{\varphi }_{\text{L}}}+{{\rho }_{\text{G}}}{{\varphi }_{\text{G}}} $ | (2) |
| $ \mu ={{\mu }_{\text{L}}}{{\varphi }_{\text{L}}}+{{\mu }_{\text{G}}}{{\varphi }_{\text{G}}} $ | (3) |
| $ \lambda ={{\lambda }_{\text{L}}}{{\varphi }_{\text{L}}}+{{\lambda }_{\text{G}}}{{\varphi }_{\text{G}}} $ | (4) |
由于各相看成一种流体,因此不管是动量方程还是能量方程都是单一求解。对于环状流动,可假设冷凝过程为稳态。求解方程如下:
体积分数方程:
| $ \nabla \cdot \left( \vec{v}{{\varphi }_{\text{G}}} \right)=\frac{{{{\dot{m}}}_{\text{G}}}}{{{\rho }_{\text{G}}}} $ | (5) |
连续性方程:
| $ \nabla \cdot \left( \rho \vec{v} \right)=0 $ | (6) |
动量方程:
| $ \nabla \cdot \left( \rho \vec{v}\vec{v} \right)=-\nabla p+\nabla \cdot \left[ \mu \left( \nabla \vec{v}+\nabla {{{\vec{v}}}^{T}} \right) \right]+\rho \vec{g}+\vec{F} $ | (7) |
为考虑表面张力的影响,本文采用BRACKBILL等[10]提出的CSF模型(continuum surface force),使表面张力可以表达成体积力的形式从而以源项的方式添加到动量方程,其表达式为:
| $ \vec{F}=\sigma \frac{2\rho {{\kappa }_{\text{L}}}\nabla {{\varphi }_{\text{L}}}}{{{\rho }_{\text{L}}}+{{\rho }_{\text{G}}}} $ | (8) |
| $ {{\kappa }_{L}}=\nabla \cdot \frac{\nabla {{\varphi }_{\text{L}}}}{\left| \nabla {{\alpha }_{\text{L}}} \right|} $ | (9) |
能量方程:
| $ \nabla \cdot \left[ \vec{v}\left( \rho E+p \right) \right]=\nabla \cdot \left( {{\lambda }_{\text{eff}}}\nabla T \right)+{{h}_{lv}}\dot{m} $ | (10) |
式中
| $ E=\frac{{{\varphi }_{\text{L}}}{{\rho }_{\text{L}}}{{E}_{\text{L}}}+{{\varphi }_{\text{G}}}{{\rho }_{\text{G}}}{{E}_{\text{G}}}}{{{\varphi }_{\text{L}}}{{\rho }_{\text{L}}}+{{\varphi }_{\text{G}}}{{\rho }_{\text{G}}}} $ | (11) |
| $ {{\lambda }_{\text{eff}}}=\lambda +\frac{{{c}_{p}}{{\mu }_{t}}}{P{{r}_{t}}} $ | (12) |
在本文的研究工况范围内,ReG的范围为17 127~252 591,而ReL的范围是210~5 293。从各相雷诺数来看,气相可以确定为完全湍流,而液相在入口段由于干度很大,可能处于层流,而层流向湍流转换的位置不能确定。本文假定气液两相一直处于湍流状态。根据DA RIVA等[11]的研究,低雷诺数的SST (shear stress transport) k-ω模型一方面可有效处理近壁区层流到湍流的过渡,另一方面,其引入了可避免涡黏性被过高预测的模型。
2.4 相变模型本文采用LEE[12]模型模拟气液两相之间的传质过程。该模型假定气液相界面为饱和温度,当控制体的温度小于饱和温度且气相分数大于0时,气相向液相传递质量。当气相体积分数为0时,传质过程不发生。
| $ {\dot m_{\rm{G}}} = - {\dot m_{\rm{L}}} = r{\varphi _{\rm{G}}}{\rho _{\rm{G}}}\frac{{\left( {T - {T_{{\rm{sat}}}}} \right)}}{{{T_{{\rm{sat}}}}}},T < {T_{{\rm{sat}}}} $ | (13) |
| $ {{\dot{m}}_{\text{G}}}=-{{\dot{m}}_{\text{L}}}=r{{\varphi }_{\text{L}}}{{\rho }_{\text{L}}}\frac{\left( T-{{T}_{\text{sat}}} \right)}{{{T}_{\text{sat}}}},T>{{T}_{\text{sat}}} $ | (14) |
本文通过UDF(user defined function)的形式将上述模型以源项的方式添加到各相的体积分数方程及能量方程中。关于系数r的确定,DA RIVA等[13]指出r太大会导致计算不收敛,太小会使相界面度严重偏离饱和温度。本文通过试错法来调整r的取值,并通过将模拟的换热系数与实验值对比来验证r的准确性。根据工况和几何结构的不同,本文r取值为3×105~1.5×106 s-1,每种情况下相界面的温度与饱和温度的差值都小于1 K。
本文采用压力基稳态求解,采用SIMPLE算法实施压力与速度的耦合,VOF方程采用隐式格式离散,操作密度设为气相密度。动量、能量、湍动能和湍动黏度方程采用三阶MUSCL格式离散。采用bounded gradient maximization (BGM)算法捕捉相界面。
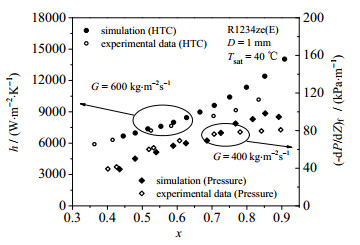
3 结果与讨论 3.1 模型验证为验证数学模型的准确性,本文将数值计算得到的结果与DEL COL等[7]的实验数据进行比较。图 2分别展示了相同工况下换热系数以及压降的模拟值与实验测量值随干度的变化关系。由图可知,本文模拟得到的换热系数和压降梯度不管是趋势上还是数值上都能和实验数据较好地符合,最大偏差分别控制在16.8%和22.8%以内,说明了本文数学模型的准确性。
|
图 2 换热系数模拟值与实验数据对比 Fig.2 Comparison of simulated HTC with experimental data of DEL COL et al. [7] |
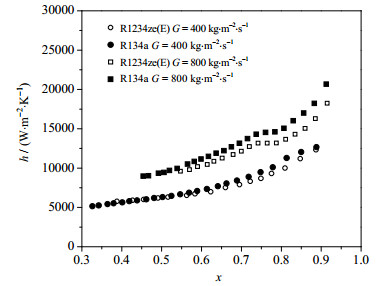
图 3展现了不同质量流速下R1234ze(E)和R134a的换热系数随干度的变化趋势。对于R1234ze(E)和R134a,换热系数都随干度和质量流速的增大而增大。当干度小于0.75时,换热系数与干度几乎成线性关系。相同质量流速和干度下,R134a的换热系数要稍大于R1234ze(E),特别是在高干度区和高质量流速的时候。当G = 800 kg·m2·s-1时,R1234ze(E)的换热系数平均要比R134a低8.87%。
|
图 3 换热系数随干度的变化 Fig.3 Profiles of condensation heat transfer coefficients as a function of vapor quality |
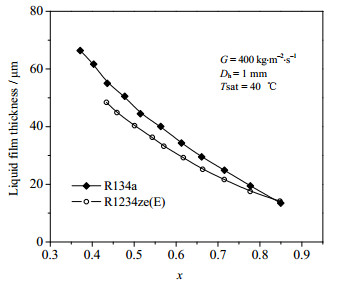
图 4展现了G = 400 kg·m-2·s-1时,R1234ze(E)和R134a局部液膜厚度随干度的变化关系。由图可知,液膜厚度随干度的增大而减小。在高干度区,管内冷凝的初始阶段,气相速度很大而液相速度很小。由于气液两相之间较大的相对速度差,产生了很大的相间剪切力,减薄了液膜厚度。相对重力和表面张力,剪切力在高干度区起主导作用。随着干度的降低,由于气液两相之间的动量交换,气相速度逐渐降低而液相速度逐渐增大,相间剪切力减小,液膜变厚。此外,尽管R134a的换热系数较高,相同工况下其液膜厚度也更厚。R1234ze(E)的液膜厚度平均要比R134a薄15.7%。由于R1234ze(E)的气液密度比相对R134a要大,因此相同质量流速和干度下,R1234ze(E)的气液相速度比更大,相间剪切力增强从而减薄了液膜厚度。本文的模拟研究假设壁温为常数,因而局部换热系数的大小和局部的热流量成正比。DA RIVA等[11]讨论了湍流效应对R134a在水平圆管内换热特性的影响,发现在高质量流速下,由于液相内部的湍流效应,局部热流量的大小不再只取决于液膜厚度,还取决于液相有效热导率的大小。
|
图 4 液膜厚度随干度的变化 Fig.4 Profiles of liquid film thickness as a function of vapor quality |
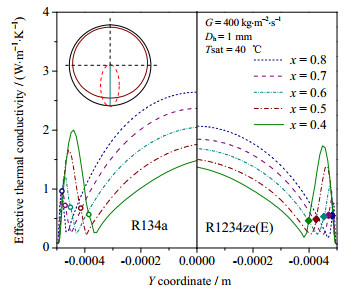
图 5展现了不同干度下有效热导率的分布。图中圆形符号和方形符号分别代表R134a和R1234ze(E)气液相界面的位置。对任意横截面(XY平面),Y = 0 m代表圆管的中心位置,Y = -0.005 m代表圆管的底部。由图可知,相同情况下R134a的有效热导率要大于R1234ze(E)。当G = 400 kg·m-2·s-1,x = 0.4和θ = 180°时,R134a液相的平均有效热导率比R1234ze(E)大28%。这或许可以解释即使R134a的液膜厚度更厚但是其换热系数仍要大于R1234ze(E)。本文的结果说明,在衡量不同工质在水平圆管内的冷凝换热特性时,液膜厚度的大小并不是决定性因素,有效热导率的影响不可忽视。
|
图 5 有效热导率沿Y轴的变化 Fig.5 Profiles of effective thermal conductivity along Y-axis |
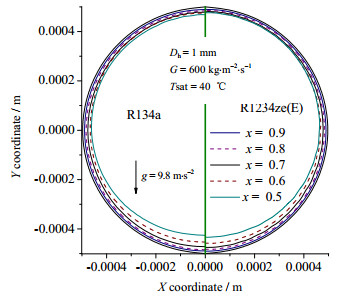
图 6展现了冷凝过程中不同干度下R134a和R1234ze(E)相界面的分布。整体来看,R1234ze(E)的相界面分布特性与R134a相似。在高干度区时,剪切力占主导,重力的影响可以忽视,液膜沿圆周均匀分布。随着干度的降低,在圆管顶部的冷凝液由于重力的作用积聚到底部,逐渐开始分层。
|
图 6 R1234ze(E)和R134a气液相界面形状 Fig.6 Liquid–vapor interfaces of R1234ze(E) and R134a |
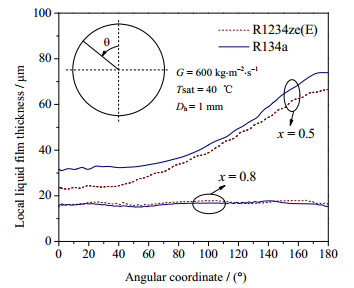
图 7展现了R1234ze(E)和R134a局部液膜厚度随周向位置的变化特性。由图可知,当干度比较高时(x=0.8),R1234ze(E)和R134a不同周向位置处的液膜厚度几乎一样。且液膜厚度几乎不随周向位置发生变化。随着干度的减小(x=0.5),R1234ze(E)的液膜厚度明显比R134a要薄,主要体现在圆管的顶部和底部位置。此外,当干度较小时,重力的影响增强,两种工质的液膜厚度都是随着角度的增大而逐渐增大。
|
图 7 局部液膜厚度沿周向位置的变化 Fig.7 Profiles of local film thickness as a function of angular coordinate |
由于目前没有可预测R1234ze(E)换热性能的关联式提出,本文尝试将现有的关联式去预测R1234ze(E)的换热系数。本文通过定义平均绝对误差(MAD)来衡量关联式的预测效果,其计算方式如下:
| $ {\rm{MAD}} = \frac{1}{N}\sum\nolimits_1^N {\left| {\frac{{{h_{{\rm{pre}}}} - {h_{{\rm{sim}}}}}}{{{h_{{\rm{sim}}}}}}} \right|} \cdot 100\% $ | (15) |
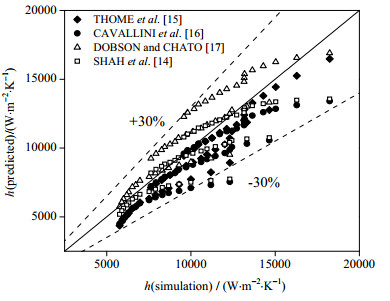
如图 8所示,现有关联式的预测误差大概在±30%以内。其中,SHAH等[14]提出的关联式预测效果最好,平均绝对误差为10.14%。THOME等[15]和CAVALLINI等[16]提出的关联式低估了本文的模拟值,MAD分别为17.27%和14.48%。而DOBSON和CHATO关联式[17]一定程度上高估了模拟值,平均绝对误差为11.48%。
|
图 8 换热系数模拟值与关联式预测值对比 Fig.8 Comparison of simulated heat transfer coefficients with predicted data |
对于管内的两相流动,两相流动压降主要由以下几部分组成:摩擦压降、加速压降和重力压降。其中,加速压降是由于进出口气液含量变化而导致的压降损失。由于本文研究的是水平管内的冷凝流动,因此重力压降可以忽略。摩擦压降等于总的压降减去加速压降,其表达式如下:
| $ {\left( { - \frac{{{\rm{d}}P}}{{{\rm{d}}z}}} \right)_{\rm{a}}} = {G^2}\frac{{\rm{d}}}{{{\rm{d}}z}}\left( {\frac{{{x^2}}}{{\varphi {\rho _{\rm{G}}}}} + \frac{{{{\left( {1 - x} \right)}^2}}}{{\left( {1 - \varphi } \right){\rho _{\rm{L}}}}}} \right) $ | (16) |
| $ {\left( { - \frac{{{\rm{d}}P}}{{{\rm{d}}z}}} \right)_{\rm{f}}} = {\left( { - \frac{{{\rm{d}}P}}{{{\rm{d}}z}}} \right)_{{\rm{tp}}}} - {\left( { - \frac{{{\rm{d}}P}}{{{\rm{d}}z}}} \right)_{\rm{a}}} $ | (17) |
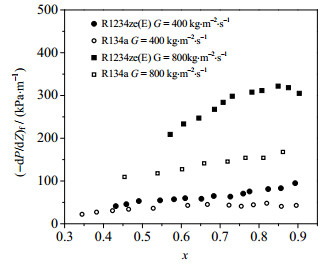
图 9展现了不同流量下R134a和R1234ze(E)摩擦压降梯度随干度的变化趋势。由图 9可知,R134a和R1234ze(E)摩擦压降梯度随干度和质量流速的增大而增大。相同情况下,R1234ze(E)的摩擦压降要大于R134a。由于R1234ze(E)的气相密度要小于R134a,相同质量流速下,其气相速度要大于R134a。与此同时,R134a和R1234ze(E)的液相黏度几乎一致。因此相同工况下,R1234ze(E)的流动阻力大于R134a。
|
图 9 压降梯度随干度的变化 Fig.9 Pressure gradients versus vapor quality |
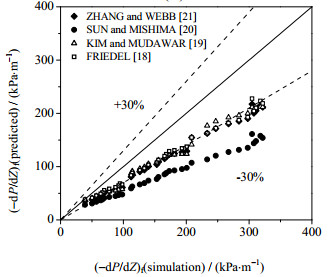
图 10展现了现有压降关联式对模拟得到的R1234ze(E)压降梯度值得预测效果。很明显,现有的关联式对R1234ze(E)的压降存在严重的低估,平均绝对误差几乎都在30%左右。其中最好的是FRIEDEL[18]提出的关联式,MAD为27.06%。
|
图 10 压降梯度模拟值与关联式预测值对比 Fig.10 Comparison of simulated pressure gradients with predicted data |
采用VOF模型对R1234ze(E)在水平圆管内的冷凝换热及阻力特性进行了数值模拟研究,讨论了质量流量、干度和物性对换热系数和压降梯度的影响。对于R1234ze(E)和R134a,换热系数和压降梯度都随干度和质量流速的增大而增大。相同情况下,R1234ze(E)换热系数小于R134a,但压降大于R134a。当G=800 kg·m-2·s-1时,R1234ze(E)的换热系数平均要比R134a低8.87%。R1234ze(E)的液膜厚度平均要比R134a薄15.7%。当气液两相都为湍流,在衡量不同工质在水平圆管内的冷凝换热特性时,有效热导率的影响要大于液膜厚度。R1234ze(E)在管内的液膜分布特性整体上和R134a相似。SHAH等提出的关联式能准确地预测R1234ze(E)的冷凝换热系数,平均绝对误差为10.14%。FRIEDEL,KIM and MUDAWAR,SUN and MISHIMA以及ZHANG and WEBB提出的压降关联式不能准确地预测R1234ze(E)的压降梯度,预测值偏小,误差在30%左右。
|
|
| [1] |
CAVALLINI A, DORETTI L, MATKOVIC M, et al. Update on condensation heat transfer and pressure drop inside minichannels[J]. Heat Transfer and Engineering, 2006, 27(4): 74-87. |
| [2] |
AWAD M M, DALKILIC A S, WONGWISES S. A critical review on condensation heat transfer in microchannels and minichannels[J]. Journal of Nanoscience and Nanotechnology, 2014, 5(1): 1-25. |
| [3] |
MOTA-BABILONI A, NAVARRO-ESBR J, MOL S F, et al. A review of refrigerant R1234ze(E) recent investigations[J]. Applied Thermal Engineering, 2016, 95(1): 211-222. |
| [4] |
WANG J, LI J M, HWANG Y. Flow pattern transition during condensation of R134a and R1234ze(E) in microchannel arrays[J]. Applied Thermal Engineering, 2017, 115(1): 244-255. |
| [5] |
LIU N, XIAO H, LI J M. Experimental investigation of condensation heat transfer and pressure drop of propane, R1234ze(E) and R22 in minichannels[J]. Applied Thermal Engineering, 2016, 102(1): 63-72. |
| [6] |
JIGE D, INOUE N, KOYAMA S. Condensation of refrigerant in a multiport tube with rectangular minichannels[J]. International Journal of Refrigeration, 2016, 67(1): 202-213. |
| [7] |
DEL COL D, BORTOLATO M, AZZOLIN M, et al. Condensation heat transfer and two-phase frictional pressure drop in a single minichannel with R1234ze(E) and other refrigerants[J]. International Journal of Refrigeration, 2015, 50(1): 87-103. |
| [8] |
HOSSAIN M A, ONAKA Y, MIYARA A. Experimental study on condensation heat transfer and pressure drop in horizontal smooth tube for R1234ze(E), R32 and R410A[J]. International Journal of Refrigeration, 2012, 35(1): 927-938. |
| [9] |
NEMA G, GARIMELLA S, FRONK B M. Flow regime transitions during condensation in microchannels[J]. International Journal of Refrigeration, 2014, 40(1): 227-240. |
| [10] |
BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. |
| [11] |
DA RIVA E, DEL COL D, GARIMELLA S V, et al. The importance of turbulence during condensation in a horizontal circular minichannel[J]. International Journal of Heat and Mass Transfer, 2012, 55(1): 3470-3481. |
| [12] |
LEE W H. A pressure iteration scheme for two-phase flow modeling[M]. Washington: Hemisphere press, 1980.
|
| [13] |
DA RIVA E, DEL COL D. Numerical simulation of laminar liquid film condensation in a horizontal circular minichannel[J]. Journal of Heat Transfer, 2012, 134(5): 1-8. |
| [14] |
SHAH M M. An improved and extended general correlation for heat transfer during condensation in plain tubes[J]. HVAC & R Research, 2009, 15(5): 889-913. |
| [15] |
THOME J R, HAJAL J E, CAVALLINI A. Condensation in horizontal tubes, part 2:New heat transfer model based on flow regimes[J]. International Journal of Heat and Mass Transfer, 2003, 46(1): 3365-3387. |
| [16] |
CAVALLINI A, DEL COL D, DORETTI L, et al. Condensation in horizontal smooth tubes:a new heat transfer model for heat exchanger design[J]. Heat Transfer and Engineering, 2006, 27(8): 31-38. DOI:10.1080/01457630600793970 |
| [17] |
DOBSON M K, CHATO J C. Condensation in smooth horizontal tubes[J]. Journal of Heat Transfer, 1998, 120(1): 193-213. |
| [18] |
FRIEDEL L. Improved friction pressure drop correlations for horizontal and vertical two-phase pipe flow[C]. Process of European Two-phase Flow Group Meet. Ispra: Paper E, 1979.
|
| [19] |
KIM S M, MUDAWAR I. Universal approach to predicting two-phase frictional pressure drop for adiabatic and condensing mini/micro-channel flows[J]. International Journal of Heat and Mass Transfer, 2012, 55(1): 3246-3261. |
| [20] |
SUN L, MISHIMA K. Evaluation analysis of prediction methods for two-phase flow pressure drop in mini-channels[J]. International Journal of Multiphase Flow, 2009, 35(1): 47-54. DOI:10.1016/j.ijmultiphaseflow.2008.08.003 |
| [21] |
ZHANG M, WEBB R L. Correlation of two-phase friction for refrigerants in small-diameter tubes[J]. Experimental Thermal and Fluid Science, 2001, 25(3/4): 131-139. |




