2. 香港科技大学 化学及生物工程学系, 香港;
3. 大连理工大学 化工学院, 化工系统工程研究所, 辽宁 大连 116024
2. Department of Chemical and Biological Engineering, Hong Kong University and Science and Technology, Hong Kong, China;
3. School of Chemical Engineering, Dalian University of Technology, Dalian 116024, China
萃取精馏已被广泛用于化学工业中以分离共沸或近沸混合物,对比常规精馏,萃取精馏的设计较难,主要是因为萃取精馏设计中存在多个设计变量,且变量间相互影响。因此,为了得到经济性最优的萃取精馏过程,国内外学者已提出多种萃取精馏过程设计方法。
Kossack等[1]提出一种系统性的萃取精馏过程设计方法。该方法利用分子设计软件生成可用的萃取剂并通过计算分离选择性筛选合适的萃取剂,再将筛选出的萃取剂代入精馏模型进行过程优化。该方法有很强的系统性,但未对体系的相平衡进行标定,从而导致明显的设计误差。鉴此,Lek-utaiwan等[2]提出了一种新的设计方法。该方法首先筛选出最合适的萃取剂,然后利用实验数据确定相平衡方程参数,再导入Aspen模拟软件进行流程模拟并通过灵敏度分析逐一改变塔的设计变量,以实现操作条件优化,提高设计的准确性,由于塔的多个设计变量之间存在相互影响,仅仅通过Aspen模拟并不能完全实现过程优化。通常,过程优化需建立严格的数学模型再利用数值算法进行求解。对于精馏过程,文献中已报道了2种模型:混合整型非线性模型和广义析取规划模型(generalized disjunctive programming,GDP)[3]。相比较而言,GDP模型更便于后续的模型求解。Caballero等[4]将Aspen模拟与GDP建模法进行耦合,有效地应用于乙醇-水的萃取分离过程优化。但该方法并未对萃取剂做出筛选。目前为止,文献中尚未有一种完整的系统性的萃取精馏严格优化设计方法。因此,本研究提出一种新的萃取精馏过程设计方法以生成经济性最优的设计方案。该方法共分3个步骤:萃取剂的筛选,相平衡方程及参数的确定,严格的萃取精馏过程数值优化。
水和醋酸的分离是醋酸生产中必不可少的过程。由于两者沸点相近,萃取精馏被认为是一种有效的分离工艺。在文献中,多种基于流程模拟的方法被应用于水-醋酸的萃取精馏过程设计。Lei等[5]选用溶剂三正丁胺以平衡塔板方程法进行模拟分析。韩淑萃等[6]以N-甲基吡咯烷酮为溶剂在RADFRAC模块中进行模拟和灵敏度分析。尽管基于流程模拟的方法可生成可行的过程设计方案,但不能对萃取精馏过程进行优化设计得到费用最低的设计方案。为此,本研究将所提出的萃取精馏优化设计方法应用于水-醋酸分离过程中,以避免文献中已有方法在相平衡准确性和流程优化方面的不足。
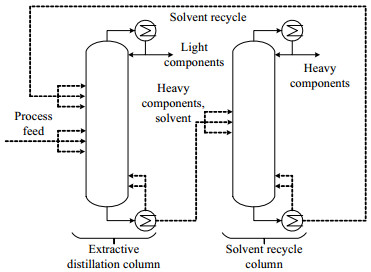
2 系统性萃取精馏过程优化设计方法如图 1所示,萃取精馏过程涉及2个塔:萃取精馏塔和溶剂回收塔。在萃取精馏塔中,萃取剂从进料混合物上方进入,塔顶可得到纯的轻组分,塔釜得到重组分和溶剂。之后,塔釜混合物进入溶剂回收塔。在回收塔中,塔顶分离出满足分离要求的重组分,塔釜得到溶剂,并返回萃取精馏塔循环使用。全流程涉及变量如表 1所示。
|
图 1 萃取精馏过程流程简图 Fig.1 Schematic diagram of extractive distillation process |
|
|
表 1 萃取精馏过程中设计自由度 Table 1 Degrees of freedom in extractive distillation process |
本研究提出的萃取精馏过程设计框架如图 2所示,包括3个步骤。第1步是搜索溶剂,通过分离过程的理论知识进行溶剂筛选;第2步为在选定溶剂的情况下,确定合适的相平衡方程并利用实验数据回归相平衡方程参数;第3步是在确定相平衡方程和参数后,通过严格的广义析取规划模型对萃取精馏塔及溶剂回收塔进行建模和优化。最终得到费用最低的萃取精馏过程设计方案,模型优化变量包括塔的总塔板数、进料位置、进料量、冷凝器和再沸器能耗等。

|
图 2 系统性的萃取精馏过程设计方法 Fig.2 Systematic design framework for extractive distillation process |
首先,在溶剂数据库和已报道文献中搜索可用的萃取剂。考虑到环境和安全等因素,美国化学学会列举了工业上常用的多种有机溶剂,如水、乙醇、二甲基甲酰胺、甲基叔丁基醚等[7]。一般情况下,这些溶剂均可作为萃取精馏过程中的备选萃取剂。之后需从众多备选萃取剂中筛选出最为合适的萃取剂以便后续的过程设计。萃取剂可依据传统的分离工程理论知识进行选择。在精馏工艺中,分离效率由轻重关键组分(A和B)的相对挥发度αA-B决定,如式(1)所示。相对挥发度越大,两组分越容易分离。
| ${\alpha _{{\rm{A - B}}}} = \frac{{{y_{\rm{A}}}/{x_{\rm{A}}}}}{{{y_{\rm{B}}}/{x_{\rm{B}}}}} = \frac{{{\gamma _{\rm{A}}}{p_{{\rm{satA}}}}}}{{{\gamma _{\rm{B}}}{p_{{\rm{satB}}}}}}$ | (1) |
式中:x和y分别为液相和气相摩尔分数;γ为活度系数;psat为纯物质的饱和蒸气压,Pa。在温度一定的条件下,纯物质的饱和蒸气压之比恒定。因此,相对挥发度由液相活度系数之比决定。在萃取剂存在的情况下,这一比值被定义为关键组分的选择性SA-B。
| ${S_{{\rm{A - B}}}} = \frac{{{\gamma _{\rm{A}}}}}{{{\gamma _{\rm{B}}}}}$ | (2) |
很显然,活度系数和选择性均由液相摩尔组成所决定。通常,萃取剂的效果随着其浓度的增大而增大。为了计算的方便,可在溶剂浓度无限大的理想情况下计算相应的选择性,即为无限稀释选择性。这一变量表示在选定萃取剂的条件下最大可能的选择性。
| $S_{{\rm{A - B}}}^\infty = \frac{{\gamma _{\rm{A}}^\infty }}{{\gamma _{\rm{B}}^\infty }}$ | (3) |
因此,根据上述理论可知,在选择合适的萃取剂时,萃取剂的加入应使得关键组分的相对挥发度、选择性或无限稀释选择性尽可能地增大。除此之外,还需要考虑新加入的萃取剂是否会产生新的共沸物。很明显,合适的萃取剂不应和任一组分存在共沸点。
2.2 确定相平衡方程和参数回归对于非理想多组分体系,常用的热力学模型(即活度系数模型)包括Wilson、NTRL、UNIFAC和UNIQUAC等[8]。模型的选择要考虑是否有实验数据以及是否有准确的模型参数。为了准确地计算体系的相平衡,使用任一活度系数模型均需要对模型参数进行回归校正。当气液相平衡实验数据已知时,可利用实验数据进行参数的回归。此时,可比较各个模型的准确性和回归过程的难易性从而选择最合适的活度系数方程。当实验数据未知,可选择UNIFAC和UNIQUAC方程进行预测,其所涉及的参数可在数据库[9]中查到。此外,在一些特定的体系中,NTRL模型参数可从Aspen或Pro-Ⅱ等软件中获取。在过程的概念设计阶段,这3种方法常被选用以生成初步的设计方案。但最终为了确保设计的准确性,对其模型参数的回归仍是必不可少的。
选定活度系数模型,将等压条件下的相平衡实验数据代入下列优化问题进行参数回归:
| $\begin{gathered} {\min _{}}\sum {_k} \sum\nolimits_i {{{\left( {{y_{{\rm{calc}}, k, i}} - {y_{{\rm{exp}}, k, i}}} \right)}^2}} \\ {\rm{s}}{\rm{.t}}{{\rm{.}}_{}}{y_{{\rm{calc}}, k, i}} = {\gamma _{k, i}} \cdot {x_{{\rm{exp}}, k, i}} \cdot \frac{{{p_{{\rm{sat}}, k, i}}}}{p} \\ {\gamma _{k, i}} = f\left( {{x_{{\rm{exp}}, k, i}}, {T_k}, p, {a_{j, jj}}} \right) \\ \end{gathered} $ | (4) |
式中:目标函数为最小化气相摩尔分数计算值ycalc与实验值yexp的差的平方和。变量为交互参数αj, jj。下标i和k分别为体系中各个组分和实验组数。xexp为液相摩尔分数实验值。p为实验压力,Pa;T为热力学温度,K;f为活度系数模型方程。饱和蒸气压为已知参数,可在数据库或文献中查找。若选择基团贡献类活度系数方程(如UNIFAC),单个基团的表面积和体积贡献值也由数据库中得到。
2.3 萃取精馏过程数值优化利用广义析取规划法对萃取精馏过程进行建模[10-11]。每块塔板上的气液相平衡由第二步中确定的相平衡方程和回归的参数计算。同时,利用精馏塔的经济性计算模型对年均设备费用和操作费用进行计算。最后,以全塔年均费用之和最小为目标函数进行严格数值优化以得到最优的设计方案。
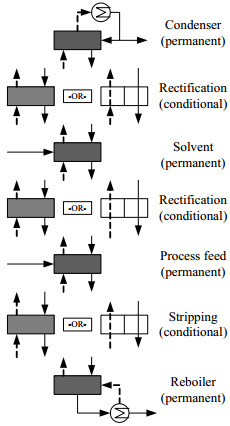
首先介绍基于广义析取规划法进行萃取精馏的建模过程。此处仅以萃取精馏塔为例进行详细描述。溶剂回收塔仅比萃取精馏塔少一块溶剂进料塔板,其余方程均一致。将全塔的塔板分为2类:永久板(permanent tray)和条件板(conditional tray),如图 3所示。永久板包括冷凝器,溶剂进料板,轻重组分进料板,再沸器。在永久板上,所有的平衡方程(即能量平衡、质量平衡、相平衡)都必须满足。两块永久板之间可能存在或不存在的塔板为条件板。塔板的存在性用布尔变量(Boolean variable)表示。当布尔变量为真时,对应的塔板存在且塔板上所有平衡方程都必须满足。当布尔变量为假时,对应的塔板不存在,可认为上升的气体和下降的液体不发生任何气液传质,仅需满足质量和能量平衡方程。最终依据布尔变量的真假来优化塔板数和物料进料板位置。基于此,组分和塔板的集合定义如下:
| $ \begin{array}{l} C = \{ 体系中的所有组分\} {\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{NST}} = \{ 萃取溶剂进料板\} \\ {\rm{NFT}} = \{ 轻重组分进料板\} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{NCT}} = \{冷凝器\} \\ {\rm{NRT}} = \{ 再沸器\} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{TM}} = \{ 条件板\} \\ {\rm{TC}} = \left\{ {{\rm{NST}}, {\rm{NFT}}, {\rm{NCT}}, {\rm{NRT}}, {\rm{TM}}} \right\} \end{array} $ |
|
图 3 广义析取规划法对萃取精馏塔的建模示意图 Fig.3 Modeling of extraction distillation column by generalized disjunctive programming |
对塔板由下到上进行排序后,进行数值优化建模。该优化问题的目标函数为最小化全过程的总年均费用(total annualized cost,TAC,CNY),包括年均设备费用(Ccp / Y,CNY)
| $\min {\rm{TAC}} = \frac{{{C_{{\rm{cp}}}}}}{Y} + {C_{{\rm{op}}}}$ | (5) |
约束条件包括全塔的一般约束、每块塔板的平衡约束条件和全塔经济性计算方程。全塔的一般约束包括全塔物料平衡(方程(6))、塔顶出料回收率和纯度要求(方程(7-8))、全塔总板数(方程(9))、气液相物质焓值计算(方程(10-13)),各物质在每块塔板上的液相活度系数(方程(14))及饱和蒸气压(方程(15))。
| ${\xi _{{\rm{F}},i}} + {\xi _{{\rm{S}},i}} = {\xi _{{\rm{D}},i}} + {\xi _{{\rm{B}},i}}\;\;\;\;\;i \in C$ | (6) |
| ${\xi _{{\rm{D}},i}} \ge {\theta _i}\left( {{\xi _{{\rm{F}},i}} + {\xi _{{\rm{S}},i}}} \right)\;\;\;\;\;i \in C$ | (7) |
| ${y_{n,i}} \ge {\tau _i}\;\;i \in C,n \in {\rm{NFT}}$ | (8) |
| ${\rm{NT}} = \sum {_{n \in {\rm{TC}}}} {\rm{ST}}{{\rm{G}}_n}$ | (9) |
| ${H_{{\rm{g}}, n, i}} = {\Delta _{\rm{f}}}{H_{{\rm{g}}, i}} + {C_{p{\rm{, mg}}, i}}\left( {{T_{{\rm{g}}, n, i}} - {T^{\rm{\Theta }}}} \right), i \in C, n \in {\rm{TC}}$ | (10) |
| ${H_{{\rm{l}}, n, i}} = {\Delta _{\rm{f}}}{H_{{\rm{l}}, i}} + {C_{p, {\rm{ml}}, i}}\left( {{T_{{\rm{l}}, n, i}} - {T^{\rm{\Theta }}}} \right), i \in C, n \in {\rm{TC}}$ | (11) |
| ${H_{{\rm{F}}, n, i}} = {\Delta _{\rm{f}}}{H_{{\rm{l, }}i}} + {C_{p, {\rm{ml}}, i}}\left( {{T_{^{\rm{F}}}} - {T^{\rm{\Theta }}}} \right), i \in C{, _{}}n \in {\rm{NFT}}$ | (12) |
| $ {H_{{\rm{S, }}n, i}} = {\Delta _{\rm{f}}}{H_{{\rm{l, }}i}} + {C_{p, {\rm{ml}}, i}}\left( {{T_{\rm{S}}} - {T^{\rm{\Theta }}}} \right), i \in C{, _{}}n \in {\rm{NST}} $ | (13) |
| ${\gamma _{n, i}} = f\left( {{x_{n, i}}, {T_{{\rm{l}}, n}}, p, {a_{j, jj}}} \right)$ | (14) |
| $ {p_{{\rm{sat}}, n, i}} = {\rm{ex}}{{\rm{p}}_{}}{\rm{(}}{A_{^i}} - \frac{{{B_{^i}}}}{{{C_{^i}} + {T_{{\rm{l}}, n}}}}{\rm{)}} $ | (15) |
式中:下标n为第n块塔板;ξF、ξS、ξD、ξB分别为轻重组分进料、溶剂进料、塔顶出料、塔釜出料的摩尔流率,kmol·h-1;θ和τ分别为塔顶出料的回收率和纯度要求;NT为全塔总的有效塔板数,等于二元变量STGn的和。当一块塔板存在时,STG=1,否则为零。Hl、Hg、HF、HS分别为物质的摩尔液态焓、气态焓、轻重组分进料、溶剂进料的摩尔焓值,J·mol-1;ΔfH表示摩尔生成焓,J·mol-1;Tl和Tg分别为塔板上液相和气相的温度,K;TF和TS分别为轻重混合物进料温度和溶剂进料温度,K;Cp, m为物质的摩尔定压热容,J·mol-1·K-1;TΘ为标准温度273.15 K。活度系数γ通过第2步中确定的活度系数模型计算。Ai、Bi、Ci为安托因方程系数。
| $\left\{\begin{array}{c} \xi_{\mathrm{s}, i}+\xi_{1, n+1, i}+\xi_{\mathrm{g}, n-1, i}-\xi_{1, n, i}-\xi_{\mathrm{g}, n, i}=0 \\ \sum\limits_{i \in C}\left(\xi_{\mathrm{s}, i} \cdot H_{\mathrm{S}, n, i}+\xi_{1, n+1, i} H_{1, n+1, i}+\xi_{\mathrm{g}, n+1, i} H_{\mathrm{g}, n-1, i}-\xi_{1, n, i} H_{1, n, i}-\xi_{\mathrm{g}, n, i} H_{\mathrm{g}, n, i}\right)=0 \\ \xi_{1, n, i}=\xi_{\mathrm{LlQ}, n} \cdot x_{n, i}, \xi_{\mathrm{g}, n, i}=\xi_{\mathrm{vAP}, n} \cdot y_{n, i} \\ \sum\limits_{i \in C} x_{n, i}=1, \sum\limits_{i \in C} y_{n, i}=1, \\ y_{n, i} p_{\mathrm{c}}=\gamma_{n, i} x_{n, i} p_{\mathrm{sat}, n, i}, T_{1, n}=T_{\mathrm{g}, n} \\ \mathrm{STG}_{n}=1 \end{array}\right\} \begin{aligned} &i \in C \\ &n \in \mathrm{NST} \end{aligned}$ | (16) |
溶剂进料板上平衡约束条件,见方程(16),包括所有的平衡方程以及相平衡方程。当回收的溶剂纯度大于99.9%,进料溶剂可假定为纯溶剂。ξl和ξg分别为物质在液相和气相中的摩尔流率,kmol·h-1。ξLIQ和ξVAP分别为塔板上液相和气相物质的总摩尔流率,kmol·h-1。pc为塔内的压力,Pa。醋酸和水进料板上的平衡约束条件(方程(17))包括所有的平衡方程以及永久塔板方程。式中ξFT为轻重组分进料的总摩尔流率,kmol·h-1。
| $ \left\{\begin{array}{c} \xi_{\mathrm{F}, n, i}+\xi_{1, n+1, i}+\xi_{g, n-1, i}-\xi_{1, n, i}-\xi_{\mathrm{g}, n, i}=0 \\ \sum\limits_{i \in C}\left(\xi_{\mathrm{F}, n, i} \cdot H_{\mathrm{F}, n, i}+\xi_{1, n+1, i} H_{1, n+1, i}+\xi_{\mathrm{g}, n+1, i} H_{\mathrm{g}, n+1, i}-\xi_{1, n, i} H_{1, n, i}-\xi_{\mathrm{g}, n, i} H_{\mathrm{g}, n, i}\right)=0 \\ \xi_{\mathrm{F}, n, i}=\xi_{\mathrm{FT}} \cdot x_{\mathrm{F}, i}, \xi_{1, n, i}=\xi_{\mathrm{LQ}, n} \cdot x_{n, i}, \xi_{\mathrm{g}, n, i}=\xi_{\mathrm{VAP}, n} \cdot y_{n, i} \\ \sum\limits_{i \in C} x_{n, i}=1, \sum\limits_{i \in C} y_{n, i}=1 \\ y_{n, i} p_{\mathrm{c}}=\gamma_{n, i} x_{n, i} p_{\text {sat }, n, i}, T_{1, n}=T_{\mathrm{g}, n} \\ \mathrm{STG}_{n}=1 \end{array}\right\} \begin{aligned} &i \in C \\ &n \in \mathrm{NFT} \end{aligned} $ | (17) |
冷凝器内平衡约束条件(方程(18))包含所有的平衡方程、露点方程、回流方程和永久塔板方程。ξDIS为塔顶出料的总摩尔流率,kmol·h-1;ψ为回流比;WNCT为冷凝器功耗,J·h-1;HD为塔顶出料的摩尔焓,J·mol-1。在冷凝器内,气相进料中各物质的摩尔分数yn-1与回流流股和塔顶出料中各物质的摩尔分数xn相等。
| $\left\{\begin{array}{c} \xi_{\mathrm{g}, n-1, i}-\xi_{1, n, i}-\xi_{\mathrm{D}, i}=0 \\ \sum\limits_{i \in C}\left(\xi_{\mathrm{l}, n-1, i} H_{\mathrm{l}, n-1, i}-\xi_{\mathrm{l}, n, i} H_{\mathrm{l}, n, i}-\xi_{\mathrm{D}, i} H_{\mathrm{D}, i}\right)=W_{\mathrm{NCT}} \\ \xi_{\mathrm{D}, i}=\psi \cdot \xi_{\mathrm{l}, n, i}, \xi_{\mathrm{D}, i}=\xi_{\mathrm{DIS}} \cdot x_{n, i} \\ \xi_{\mathrm{l}, n, i}=\xi_{\mathrm{LIQ}, n} \cdot x_{n, i}, \xi_{\mathrm{g}, n, i}=\xi_{\mathrm{VAP}, n} \cdot y_{n, i} \\ y_{n-1, i}=x_{n, i}=y_{n, i}, \sum\limits_{i \in C} x_{n, i}=1, \sum\limits_{i \in C} y_{n, i}=1 \\ \sum\limits_{i \in C}\left(\gamma_{n, i} x_{n, i} p_{\mathrm{sat}, n, i}\right)=p_{\mathrm{c}}, T_{1, n}=T_{\mathrm{g}, n} \\ \mathrm{STG}_{n}=1 \end{array}\right\} \begin{aligned} &i \in C \\ &n \in \mathrm{NCT} \end{aligned}$ | (18) |
| $\left\{\begin{array}{c} \xi_{1, n+1, i}-\xi_{\mathrm{B}, i}-\xi_{\mathrm{g}, n, i}=0 \\ \sum\limits_{i \in C}\left(\xi_{\mathrm{l}, n+1, i} H_{1, n+1, i}-\xi_{\mathrm{g}, n, i} H_{\mathrm{g}, n, i}-\xi_{\mathrm{B}, i} H_{\mathrm{B}, i}\right)=W_{\mathrm{NRT}} \\ \xi_{\mathrm{BOT}}=\xi_{\mathrm{s}}+\xi_{\mathrm{FT}}-\xi_{\mathrm{DIS}}, \xi_{\mathrm{B}, i}=\xi_{\mathrm{l}, n, i} \\ \xi_{\mathrm{l}, n, i}=\xi_{\mathrm{LlQ}, n} \cdot x_{n, i}, \xi_{\mathrm{g}, n, i}=\xi_{\mathrm{VAP}, n} \cdot y_{n, i} \\ \sum\limits_{i \in C} x_{n, i}=1, \sum\limits_{i \in C} y_{n, i}=1, \\ \sum\limits_{i \in C}\left(\gamma_{n, i} \cdot x_{n, i} \cdot p_{\mathrm{sat}, n, i}\right)=p_{c}, T_{1, n}=T_{\mathrm{g}, n} \\ \mathrm{STG}_{n}=1 \end{array}\right\} \begin{aligned} &i \in C \\ &n \in \mathrm{NRT} \end{aligned}$ | (19) |
再沸器内平衡约束(方程(19))包含所有平衡方程、泡点方程、永久板方程。WNRT为再沸器的功耗,J·h-1;HB为塔底出料的摩尔焓,J·mol-1;ξBOT为塔底出料的总摩尔流率,kmol·h-1,由全塔的物料平衡所决定。
| $ \left\{\begin{array}{c} \xi_{1, n+1, i}+\xi_{g, n-1, i}-\xi_{1, n, i}-\xi_{g, n, i}=0 \\ \sum\limits_{i \in C}\left(\xi_{1, n+1, i} H_{1, n+1, i}+\xi_{g, n-1, i} H_{g, n-1, i}-\xi_{1, n, i} H_{1, n, i}-\xi_{g, n, i} H_{g, n, i}\right)=0 \\ \xi_{\text {LQ }, n}=\sum\limits_{i \in C} \xi_{1, n, i}, \xi_{\mathrm{VAP}, n}=\sum\limits_{i \in C} \xi_{g, n, i} \\ \xi_{1, n, i}=\xi_{\mathrm{Ll}, n} \cdot x_{n, i}, \xi_{\mathrm{g}, n, i}=\xi_{\mathrm{VAP}, n} \cdot y_{n, i} \end{array}\right\} \begin{aligned} &i \in C \\ &n \in \mathrm{TM} \end{aligned} $ | (20) |
| $\left[\begin{array}{c} Z_{n} \\ y_{n, i} \cdot p_{\mathrm{c}}=\gamma_{n, i} x_{n, i} p_{\mathrm{sat}, n, i} \\ T_{1, n}=T_{\mathrm{g}, n} \\ \mathrm{STG}_{n}=1 \end{array}\right] \bf{V}\left[\begin{array}{c} \neg Z_{n} \\ x_{n, i}=x_{n+1, i}, y_{n, i}=y_{n+1, i} \\ \xi_{\mathrm{l}, n, i}=\xi_{1, n+1, i}, \xi_{\mathrm{g}, n, i}=\xi_{\mathrm{g}, n-1, i} \\ T_{1, n}=T_{1, n+1}, T_{\mathrm{g}, n}=T_{\mathrm{g}, n-1} \\ \mathrm{STG}_{n}=0 \end{array}\right] \begin{aligned} &i \in C \\ &n \in \mathrm{TM} \end{aligned}$ | (21) |
条件板的模型方程分为2部分。第1部分包括物料和能量平衡方程,如方程(20)所示。无论塔板是否存在,这些方程都必须成立。第2部分如方程(21)所示,当布尔变量Zn为真时,该条件板存在且气液相物流于塔板上发生传质并达到新的相平衡。当布尔变量为假时,该条件板不存在,因此气液相浓度组成均不发生任何变化。
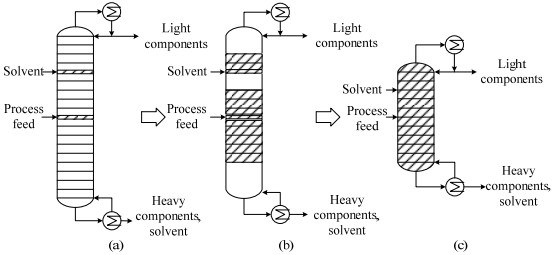
全塔的初始设定如图 4(a)所示。经过求解器优化后,一些布尔变量被设定为真,另一些为假。由于可能会出现不同塔板组合方式但分离效果一样的结果,如下逻辑约束条件用于避免重复解。
| ${Z_n} \leqslant {Z_{n - 1}}{, _{}}{\rm{NCT}} > n > {\rm{NST}}$ | (22) |
| ${Z_n} \leqslant {Z_{n - 1}}{, _{}}{\rm{NST}} < n < {\rm{NFT}}$ | (23) |
| ${Z_{n - 1}} \leqslant {Z_n}{, _{}}{\rm{NRT}} < n < {\rm{NFT}}$ | (24) |
|
图 4 广义析取规划精馏模型的萃取精馏塔优化机制 Fig.4 Optimization mechanism of extractive distillation column based on GDP distillation model |
方程(22)表示在溶剂进料板上方,所有存在的塔板必须靠近该进料板。方程(23~24)表示在轻重组分进料口上方或下方,存在的塔板也必须靠近该板, 见图 4(b)。最终,将布尔变量为假的塔板删去后可得到最优的全塔设计,如图 4(c)所示。全塔的设计决定整个萃取精馏过程的费用,包含2个部分:设备费用和能耗费用。如方程(25)所示,设备费用主要包括塔壳费用Csh、塔内装置费用Cint、冷凝器及再沸器的费用Ccb[12]。
| ${C_{{\rm{cp}}}} = {C_{{\rm{sh}}}} + {C_{{\rm{int}}}} + {C_{{\rm{cb}}}}$ | (25) |
假定2个塔均为筛板塔,塔壳费用和塔内部装置费可由方程(26-27)计算得到
| ${C_{{\rm{sh}}}} = {C_1}{d_{{\rm{col}}}}{h_{{\rm{col}}}}$ | (26) |
| ${C_{\operatorname{int} }} = {C_2}{d_{{\rm{col}}}}\delta {\rm{NT}}$ | (27) |
式中:C1和C2为价格参数,CNY;dcol和hcol为塔的直径和塔高,m;δ为两块塔板间的间距,m;塔高由有效塔板数NT决定,见方程(28)。塔的直径由塔底上升气体的体积决定。
| ${h_{{\rm{col}}}} = {\rm{NT}} \cdot \delta + {h_0}$ | (28) |
| ${d_{{\rm{col}}}} = \sqrt {\frac{{2{\xi _{VAP, n}}}}{{\rm{ \mathit{ π} }}}\sqrt {\frac{{R{T_n}\sum {{y_{n, i}}{M_i}} }}{{{p_{\rm{c}}}}}} } {, _{}}n \in {\rm{NRT}}$ | (29) |
式中:h0为塔顶的高度,m;Mi为摩尔质量,g·mol-1。冷凝器和再沸器均按普通换热器计算费用。
| ${C_{{\rm{cb}}}} = {C_{{\rm{hex}}}}{\left( {{A_{{\rm{NCT}}}} + {A_{{\rm{NRT}}}}} \right)^{0.65}}$ | (30) |
| ${A_{{\rm{NCT}}}} = \frac{{{W_{{\rm{NCT}}}}}}{{{K_m}\Delta {T_{{\rm{NCT}}}}}}, {A_{{\rm{NRT}}}} = \frac{{{W_{{\rm{NRT}}}}}}{{{K_m}\Delta {T_{{\rm{NRT}}}}}}$ | (31) |
式中:Chex为换热器设备费用参数,CNY;ANCT和ANRT分别为冷凝器和再沸器换热面积,m2;Km为传热系数,W·m-2·K-1;ΔTNCT和ΔTNRT分别为冷凝器和再沸器对数平均温差,K。全塔的能耗费用由消耗的冷凝水质量流量(mcw,t·h-1)和过热蒸气质量流量(mst,t·h-1)决定。工业上冷凝器中冷却水进口和出口温差为40 K,冷却水的消耗量由冷凝器功耗决定(方程(33))。过热蒸气消耗量由塔釜再沸器功耗决定(方程(34))。
| ${C_{{\rm{op}}}} = \left( {{m_{{\rm{cw}}}}{C_{{\rm{cw}}}} + {m_{{\rm{st}}}}{C_{{\rm{st}}}}} \right){t_{{\rm{op}}}}$ | (32) |
| ${m_{{\rm{cw}}}} = \frac{{{W_{{\rm{NCT}}}}}}{{40{c_{{\rm{water}}}}}}$ | (33) |
| ${m_{{\rm{st}}}} = \frac{{{W_{{\rm{NRT}}}}}}{{{\rm{LT}}}}$ | (34) |
式中:Ccw和Cst分别为冷凝水和过热蒸气的单价,CNY·t-1。cwater为水的比热容,即4.1813 J·kg-1·K-1。LT表示使用的过热蒸气的潜热,J·t-1。top为全年的运行时间,h。
全过程的费用取决于模型中变量的取值,如布尔变量的真假和回流比。当确定所需的物性参数和价格参数后,将两塔模型于GAMS平台中编译求解,最终可得到最小年均生产费用时所有变量的取值。求解GDP模型有2种方法:1) 用logic-based OA算法;2) 用JAMS求解器中的big-M或convex-hull法将GDP模型转化为MINLP模型,再用已有求解算法(如DICOPT和SBB)求解。第2种方法较为常见且易于操作。考虑到精馏模型拥有较强的非线性,选择SBB求解器一般更为有效。
3 水-醋酸萃取精馏优化 3.1 筛选萃取剂对于水和醋酸体系,文献中已报道多种可用的萃取剂[12-13],如环丁砜、N-甲基吡咯烷酮、二甲亚砜等。利用方程(3)及UNIFAC方程可以计算该3种溶剂的选择性。当在环丁砜无限稀释条件下,水-醋酸的选择性Swater-AC=3.1;当使用N-甲基吡咯烷酮时,Swater-AC=6.2;当选择二甲亚砜时,Swater-AC=5.6。当加入N-甲基吡咯烷酮时,水和醋酸的选择性最高且三组分混合物中无共沸物出现。因此,可选择N-甲基吡咯烷酮(N-methylpyrrolidone,NMP)作为萃取精馏分离水-醋酸最合适的萃取剂。这一结果与文献[13]中筛选结果一致。
3.2 确定相平衡方程和参数回归对于水-醋酸-N-甲基吡咯烷酮体系而言,畅伟贤等[14]比较了NRTL、Wilson、UNIQUAC 3种活度系数方程的准确性,其中NRTL效果最好。但其仅报道了部分拟合的交互参数,并非全部结果。考虑到算例的完整性,必须重新回归热力学模型。此外,考虑到参数回归的难易程度和模型的适用性,同时回归了NRTL和UNIFAC模型,结果显示UNIFAC误差略小。因此,本研究选择UNIFAC活度系数方程。UNIFAC方程共涉及3种基团参数:基团表面积、基团体积、基团的二元交互参数。基团表面积和基团体积均可在数据库中得到且不随体系的改变而变化,仅基团的二元交互参数在不同的体系中需重新标定。畅伟贤等[14]在压力为101.33 kPa的等压条件下测定了15组不同的气液相平衡组成。将这15组实验数据代入方程(4)所列的最小化优化问题中可回归得到UNIFAC二元交互参数αj, jj,所得结果如表 2所示。
|
|
表 2 水-醋酸-N-甲基吡咯烷酮体系的UNIFAC二元交互参数 Table 2 UNIFAC interaction parameters of water, AC and NMP |
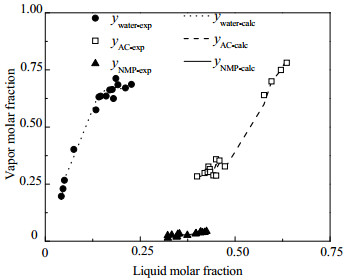
如图 5所示为气相摩尔分数计算值与实验值进行对比。图中ywater-calc、yAC-calc、yNMP-calc和ywater-exp、yAC-exp、yNMP-exp分别为水、醋酸、N-甲基吡咯烷酮的气相摩尔分数计算值和实验值。从图中可以看出,计算值与实验值十分吻合。通过计算可知平均误差小于6%。因此,可确定得到的交互参数能够准确地模拟体系的气液相平衡。
|
图 5 气相摩尔分数实验值和计算值对比 Fig.5 Comparison of experimental and calculated gas phase molar fraction (AC: 醋酸,NMP: N-甲基吡咯烷酮) (AC: acetic acid, NMP: N-methylpyrrolidone) |
在确定相平衡方程和参数后,将进行全过程的严格数值优化。对于水-醋酸-N-甲基吡咯烷酮体系,表 3列出了所需的物性参数,如安托因系数,比热容,生成焓等。表 4列出了工业上精馏中所用设备和能耗的均价以及相关的分离参数(如分离要求、进料组成、模型初始设计等)。这些参数可直接代入萃取精馏过程模型进行全流程优化。
|
|
表 3 水、醋酸、N-甲基吡咯烷酮的物性参数 Table 3 Physical parameters of water, AC and NMP |
|
|
表 4 醋酸和水萃取精馏过程费用参数和分离参数 Table 4 Cost and separation parameters of AC and water extractive distillation process |
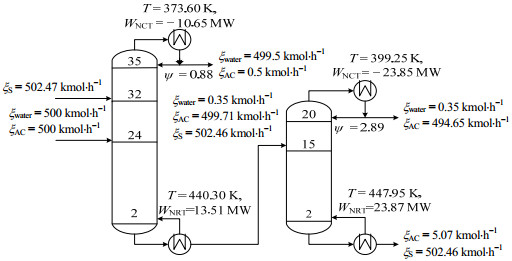
如图 6所示为优化后的萃取精馏过程示意图。图中ξwater和ξAC分别为水和醋酸的摩尔流率。在萃取精馏塔中,水和醋酸的进料位置为第24块塔板,溶剂进料位置为第32块塔板,全塔共需要36块塔板(含冷凝器)。N-甲基吡咯烷酮的进料摩尔流率ξS=502.47 kmol·h-1,回流比ψ=0.88。塔顶近乎为纯水(质量分数为99.9%),所以塔顶的温度(即373.6 K)近似水的露点温度。而塔釜为N-甲基吡咯烷酮体和醋酸的混合物,其泡点温度为440.30 K。溶剂回收塔中,最优回流比为2.89,最优塔板数为21块(含冷凝器和再沸器),进料在第15块塔板上。如表 5所示列出了两塔的具体设计方案和费用的分布。从表中可以看出,过热蒸气的使用为主要的生产费用,这与精馏工业中的现实情况相符。此外,通过计算可知,生产1 kg醋酸产品所消耗的蒸气量为4.5 MJ。而利用传统方法(即单一变量灵敏度分析法,见参考文献[6])所得最优结果为8.9 MJ每千克醋酸。因此可以发现,本文的方法能明显降低能耗和生产费用。
|
图 6 经济性最优的醋酸水萃取精馏过程 Fig.6 Optimal extractive distillation process of AC-water |
|
|
表 5 萃取精馏塔和溶剂回收塔的设计和费用分布 Table 5 Detailed design and costs for extractive distillation and solvent recovery column |
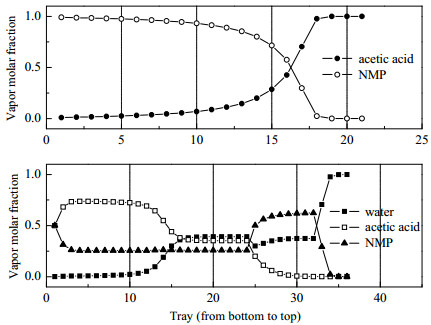
如图 7所示为两塔内各物质的液相摩尔分数xi变化曲线。在萃取精馏塔中,水为最轻的组分,因此其组成由塔顶向塔釜逐渐减小。此外,因为萃取剂从第32块板上进料起到了稀释水的作用,所以水在第32块板上的组成明显变小。但水的摩尔组成在第24块板上反而变大,这是因为进料混合物的加入导致水的组成增大至接近0.5。对于萃取剂N-甲基吡咯烷酮而言,从第32块板进入后,在第24~32块板的区间主要通过萃取作用从水-醋酸混合物中萃取出醋酸,实现醋酸浓度的迅速富集,从而实现两者的有效分离。在溶剂回收塔中,由于水在塔内的液相组成太小,所以并未展现于图中。醋酸的摩尔分数由塔釜向塔顶逐渐增加而N-甲基吡咯烷酮摩尔分数逐步降低,这与常规的精馏操作原理相吻合。
|
图 7 萃取精馏塔和溶剂回收塔内的气相组成变化 Fig.7 Changes of gas phase composition in extractive distillation and solvent recovery column |
如表 6所示为两塔严格优化模型的规模统计。整个优化模型包含5 691条方程,4 682个单变量,106个布尔变量,以及10 373个非线性矩阵。由此可见全模型规模较大,有较强非线性,这带来较大的求解难度。求解过程中,上下界间隔初始值为1.03,经过11.5 h的计算后,上下界间隔减小至0.09达到收敛,得到最优解。根据作者的经验,由于精馏模型中存在强非线性的热力学方程,big-M法较为适合被用于转化GDP模型。初值的设定也极为重要,为了加速收敛,可预先对过程进行模拟,将所得模拟结果定为初值。在利用SBB求解时,若一定时间内(如0.5 h)无法得到可行解,则表明初值较差,此时调整初值较为合适。
|
|
表 6 两塔严格优化模型的规模统计 Table 6 Model statistics for optimization of extractive distillation process |
本研究提出了一种系统性的萃取精馏过程优化设计方法,主要包括萃取剂的选择、相平衡参数的标定、严格的过程优化。最终可得到经济性最优的(即设备费用和操作费用之和最小的)萃取精馏过程设计方案。为了证明此方法的系统性和实用性,将所提出的方法应用于醋酸-水萃取精馏过程设计中,并成功地得到最优的设计方案。很显然,所提出的设计方案可推广应用于任意的萃取精馏过程设计问题中,并不局限于醋酸和水体系。在实际工业应用中,在筛选萃取剂时可同时选择2个或多个较好的萃取剂并代入后续步骤以确保获得最优的结果。此外,为了确保优化结果的可靠性,进行数值优化时可选用不同的初值来尽量避免得到较差的局部最优值。
| [1] |
KOSSACK S, KRAEMER K, GANI R, et al. A systematic synthesis framework for extractive distillation processes[J]. Chemical Engineering Research and Design, 2008, 86(7): 781-792. DOI:10.1016/j.cherd.2008.01.008 |
| [2] |
LEK-UTAIWAN P, SUPHANIT B, DOUGLAS P L, et al. Design of extractive distillation for the separation of close-boiling mixtures: Solvent selection and column optimization[J]. Computers & Chemical Engineering, 2011, 35(6): 1088-1100. |
| [3] |
BARTTFELD M, AGUIRRE POA, GROSSMANN I E. Alternative representations and formulations for the economic optimization of multicomponent distillation columns[J]. Computers & Chemical Engineering, 2003, 27(3): 363-383. |
| [4] |
CABALLERO J A, MILAN-YANEZ D. GROSSMANN I E. Optimal synthesis of distillation columns: Integration of process simulators in a disjunctive programming environment[J]. Computer Aided Chemical Engineering, 2005, 20: 715-720. |
| [5] |
ZHIGANG L, CHENGYUE L, YINGXIA L, et al. Separation of acetic acid and water by complex extractive distillation[J]. Separation and Purification Technology, 2004, 36(2): 131-138. DOI:10.1016/S1383-5866(03)00208-9 |
| [6] |
韩淑萃, 杨金杯. NMP萃取精馏分离醋酸和水的过程模拟[J]. 广东化工, 2012, 39(9): 177-181. HAN S C, YANG J B. Simulation study of the separation of Acetic acid and water by extractive distillation with NMP[J]. Guang Dong Hua Gong, 2012, 39(9): 177-181. |
| [7] |
美国化学学会. 工业常用溶剂[DB/OL]. [2018-05-15] https://www.organicdivision.org/wp-content/uploads/2016/12/organic_solvents.html. American Chemical Society. Common solvents used in organic chemistry[DB/OL]. https://www.organicdivision.org/wp-content/uploads/2016/12/organic_solvents.html. |
| [8] |
Aspen Plus User Guide, Chapter 7 Guidelines for choosing a property method[R]. Bedford USA: Aspen Technology 2000.
|
| [9] |
WITTIG R, LOHMANN J, GMEHLING J. Vapor-liquid equilibria by UNIFAC group contribution. 6. revision and extension[J]. Industrial & Engineering Chemistry Research, 2003, 42(1): 183-188. |
| [10] |
YEOMANS H, GROSSMANN I E. Disjunctive programming models for the optimal design of distillation columns and separation sequences[J]. Industrial & Engineering Chemistry Research, 2000, 39(6): 1637-1648. |
| [11] |
YEOMANS H, GROSSMANN I E. Optimal design of complex distillation columns using rigorous tray-by-tray disjunctive programming models[J]. Industrial & Engineering Chemistry Research, 2000, 39(11): 4326-4335. |
| [12] |
樊冬娌, 曹宇锋. 萃取精馏分离醋酸-水体系的模拟计算及实验研究[J]. 化学世界, 2014, 6: 359-362. FAN D L, CAO Y F. Simulation and experimental study on extractive distillation for acetic acid-water system[J]. Chemical World, 2014, 6: 359-362. |
| [13] |
胡兴兰, 刘纵宇, 孙杨, 等. 萃取精馏法分离醋酸-水的研究[J]. 环境污染治理技术与设备, 2006, 7(11): 80-83. HU X L, LIU Z Y, SUN Y, et al. Study of separation of acetic acid and water by extractive distillation[J]. Techniques and Equipment for Environmental Pollution Control, 2006, 7(11): 80-83. |
| [14] |
畅伟贤, 管国锋, 姚虎卿. 水-醋酸-N-甲基吡咯烷酮体系等压汽液平衡研究[J]. 化学工程, 2007, 35(1): 40-44. CHANG W X, GUAN G F, YAO H Q. Isobaric vapor-liquid equilibrium for water-acetic-acid-N-methyl pyrrolidone[J]. Chemical Engineering, 2007, 35(1): 40-44. |




