2. 瑞典 隆德大学 能源科学系, 瑞典 隆德 22100
2. Department of Energy Sciences, Lund University, Lund 22100, Sweden
随着科技的不断发展,微液滴因其独特的流体力学特性和尺寸效应,被广泛应用于生命科学、医学、动力、化工、采矿、核能、环境、石油、冶金、食品加工等领域[1~3]。微液滴的制备是微液滴应用的前提,流动聚焦型微通道生成的微液滴因其尺寸范围较广、大小可控、单分散性较好,且对表面材料润湿性要求不高而受到人们的关注。
近年来,许多研究人员对流动聚焦型微通道内微液滴的生成开展了研究,其中一部分学者对液滴的生成机理进行了深入的实验研究。例如,Cubaud等[4]通过实验,得到了在方形截面的十字型微通道内微液滴的五种生成机制。Costa等[5]通过实验研究了在流动聚焦型微通道内决定液滴生成机制的主要因素。Van等[6]针对流动聚焦型微通道内弹状液滴的生成机制进行了实验研究。
在研究微液滴的生成机理方面,数值模拟是另一种有效的方法。Cherlo等[7]将实验和数值模拟相结合,研究了在不同操作条件和物性参数条件下,液-液两相流的弹状和层流状的流动机制。刘检朴[8]通过实验和数值模拟研究了流动聚焦型微通道内液滴生成的机理研究,分析了连续相黏度、连续相流速、界面张力等因素的影响。Li等[9]改变了影响液滴尺寸和生成速度的条件,通过实验与数值模拟相结合的方式研究了液滴生成频率的变化趋势以及连续相和分散相的输运特性。Mohammad等[10]通过数值模拟研究了在对称流动聚焦型微通道内,连续相的黏弹性对液滴的形成和动力学的影响。王维萌等[11]运用流体体积(VOF)模型模拟研究了十字型微通道内油包水微液滴的形成过程。Chekifi等[12]同样采用VOF模型,得到了与王维萌等相同的结论,并进一步确定了包括表面张力、毛细管数和主流道宽度等参数在内的液滴生成的最佳条件。Wu等[13]和Gupta等[14]基于格子玻尔兹曼模型的数值模拟,研究了毛细管数和液体的黏弹性对液-液两相流在十字型微通道内液滴生成特点的影响。
在流动聚焦型微通道内,液滴的生成除了与液体的性质及入口流速等因素有关外,还与微通道的结构有关,有学者针对微通道的结构进行了研究。Castrohernandez等[15]先通过数值模拟计算,优化了微通道几何尺寸,然后基于数值模拟结果进行实验研究,在通道宽度为50 μm的模型中得到了直径接近于1 μm微液滴,这对流动聚焦型微通道的实际应用有突破性的意义。Chen等[16]通过可视化实验,研究了在十字型微通道的交叉接口处下游方向连接一个缩放喷嘴管后液滴的生成情况。Gulati等[17]在十字型微通道模型的交叉连接处将直角加工成一系列半径不等的圆角,研究液滴的生成情况。
从目前的研究结果来看,流动聚焦型微通道内液滴的生成主要与液体入口流速、液体的黏弹性、表面张力、微通道的几何尺寸等因素有关,其中两相流体的入口流速对于液滴的生成更是起到了十分重要的作用。目前关于入口流速对液滴生成影响的研究,主要停留在定常流速的阶段,但在实际的运用中,难免会出现入口流速不稳定的情况。例如在实验中使用的蠕动泵,当时间尺度足够小时,其提供的推动力是周期性变化的,这种周期性的变化可以看作是对液滴生成的扰动。本文假设分散相的入口流速受到外界的周期性扰动,随时间以正弦函数规律变化,运用VOF模型,通过User-Defined Function(UDF)导入分散相入口流速的函数,进行数值模拟,来探究周期性扰动对十字型微通道内微液滴生成的影响。
2 物理模型及数值算法 2.1 表面张力模型VOF模型通过引入流体体积函数V,计算各网格单元内两相的体积分数,来捕捉两相的界面。在一个网格单元内,Vc(连续相体积函数)与Vd(分散相体积函数)之和恒等于1。显然,若Vc=1或Vd=1,则说明该网格单元内不包含两相界面,即该控制体内全为连续相或全为分散相;若0 < Vc < 1,代表该网格单元内存在两相界面,也就是说该网格单元内既有连续相也有分散相。在网格单元内,流体密度ρ和黏度μ等参数均以两相流体体积的加权平均值来计算:
| $ \rho = {V_{\rm{c}}}{\rho _{\rm{c}}} + {V_{\rm{d}}}{\rho _{\rm{d}}} $ | (1) |
| $ \mu = {V_{\rm{c}}}{\mu _{\rm{c}}} + {V_{\rm{d}}}{\mu _{\rm{d}}} $ | (2) |
其中,在VOF模型中对体积函数V的扩散方程求解,以连续相为例,如式(3)所示:
| $ \frac{{\partial {V_{\rm{c}}}}}{{\partial t}} + v \cdot \nabla {V_{\rm{c}}} = 0 $ | (3) |
式中,v为速度项。
在VOF模型中采用表面张力源项用来模拟微尺度条件下的表面张力,如式(4)所示:
| $ F = 2\gamma \frac{{\rho {\kappa _{\rm{c}}}\nabla {V_{\rm{c}}}}}{{{\rho _{\rm{c}}} + {\rho _{\rm{d}}}}} $ | (4) |
式中,γ为两相表面张力系数;κc为界面曲率,可通过对相界面单位法向量求散度获得:
| $ {\kappa _{\rm{c}}} = \nabla \cdot \hat n $ | (5) |
在远离壁面的网格内,可对连续相体积分数Vc取梯度求出相界面单位法向量:
| $ \hat n = \frac{n}{{\left| n \right|}}, n = \nabla \cdot {V_{\rm{c}}} $ | (6) |
在邻近壁面的网格内,两相流体以固定的角度和壁面接触,可用接触角模型来表征壁面润湿性的影响。接触角θc可定义为在固壁面、连续相及分散相三者交界面处,两相流体相界面与固液相界面的夹角。在该模型中贴近壁面的网格内单位法向量可由式(7)计算得到:
| $ \hat n = {\hat n_{\rm{c}}}{\rm{cos}}{\theta _{\rm{c}}} + {\hat t_{\rm{c}}}{\rm{sin}}{\theta _{\rm{c}}} $ | (7) |
式中,
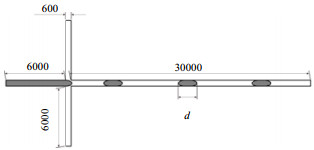
三维数值模拟计算的几何模型如图 1所示,十字型微通道的两条竖直段相对于水平段对称,竖直段为连续相的入口段,十字交叉处左边的水平段为分散相的入口段,右边为两相混合流动的直管段。竖直段和水平段的截面均为正方形,微通道宽度W=600 μm,为避免入口效应对模拟结果的影响,将连续相与分散相的入口段长度均设置为10W,两相混合流动直管段的长度为50W。液滴的尺寸由液滴的最大长度d表示。
|
图 1 十字型微通道几何模型 Fig.1 Geometric model of the cross-junction microchannel |
十字型微通道三维模型使用正六面体网格进行划分,为消除网格尺寸对模拟结果的影响,选取连续相和分散相入口流速均为0.01 m·s-1的工况,进行网格无关性验证。当网格尺寸分别取40 μm和45 μm时模拟所得的液滴尺寸之间的误差仅为0.95%,因此可以认为当网格尺寸为40 μm时,模拟结果不受网格尺寸的影响,此时网格总数为271800。
2.3 模型结构参数设置本文的数值模拟计算中,以硅油为连续相,以水为分散相,流体的物性参数如表 1所示。
|
|
表 1 流体物性参数 Table 1 Physical parameters of the materials used |
为了探究在十字型微通道内,分散相的入口流速为非定常值时对微液滴的尺寸和生成频率有何影响,首先模拟uc=ud=0.01 m·s-1时的液滴生成情况,得出液滴的生成周期为0.08 s,尺寸d =1237.5 μm。假设分散相入口流速为时间的正弦函数,拟通过改变函数的周期和振幅,来探究液滴生成情况。用T、A分别代表正弦函数的周期和振幅。在本数值模拟研究中,采用控制变量法。在研究正弦函数周期对液滴生成的影响时,取入口流速函数所能达到的最大振幅A=0.01,周期T分别取为0.08 s的0.5、1、1.5和2倍。在研究正弦函数的振幅对液滴生成的影响时,取周期为T = 0.08 s,振幅分别取为0.0025、0.005、0.0075和0.01。正弦函数的基本形式为u = 0.01+A sin(2πt/T),分散相入口流速的函数具体如表 2和表 3所示。运用UDF将编写函数的程序导入。在设置边界条件时,连续相入口选用velocity-inlet,velocity magnitude选择constant并填入0.01 m·s-1;分散相入口选用velocity-inlet,velocity magnitude选择udf选项,出口选用outflow,其余壁面均为wall,接触角设为180°。
|
|
表 2 不同周期的分散相入口流速函数 Table 2 Inlet velocity functions of the dispersion phase at different cycles |
|
|
表 3 不同振幅的分散相入口流速函数 Table 3 Inlet velocity functions of the dispersion phase at different amplitudes |
采用PISO作为压力速度耦合算法,选用PRESTO!作为压力差值算法,时间离散方式为一阶隐式格式,动量方程离散方式为二阶迎风差分格式。经过验证,时间步长设为1×10-4时既能保证模拟的精度,又能减小计算的规模。亚松弛迭代因子等参数可根据计算时结果的稳定性及收敛性选取。
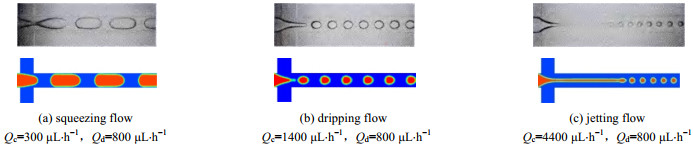
3 数值模拟方法的有效性王维萌等[18]运用VOF模型模拟出了十字型微通道内的两相流体流动情况,在不同的工况组合下,得到了拉伸挤压流型、滴状剪切流型、单分散射流流型等,并通过可视化实验得到了与数值模拟高度吻合的结果,以此证明数值模拟的有效性。本文采用上一节所述的方法,对相同的工况进行数值模拟,得到了相同的结果,如图 2所示,其中,Qc为连续相流量,Qd为分散相流量。为进一步验证该方法的有效性,将数值模拟所得的各流型的液滴尺寸与王维萌等[18]的试验结果进行比较,结果如表 4所示,可见液滴尺寸的模拟值和实验值吻合度较高,最大误差为6.18%。结合以上两点,可以说明本文的数值模拟方法有效。
|
图 2 实验(上)与数值模拟(下)流型对比 Fig.2 Comparison of experimental (top) and numerical (bottom) flow pattern results |
|
|
表 4 液滴尺寸实验值与数值模拟值比较 Table 4 Comparison of experimental and numerical simulated droplet sizes |
本节主要讨论在正弦函数形式的分散相入口流速下的液滴生成情况,具体分析正弦函数的周期和振幅两个方面的影响,下面具体讨论。
4.1 正弦函数的周期对液滴生成的影响为探究分散相入口流速为正弦函数变化时,函数周期对液滴生成的影响,本文采用了入口流速函数所能达到的最大振幅A=0.01,周期分别为T = 0.04、0.08、0.12、0.16 s的正弦函数作为分散相入口流速函数进行数值计算,数值模拟得到的液滴形态如图 3所示。

|
图 3 不同周期下分散相入口流速为正弦函数时的液滴形态 Fig.3 Droplet morphology of the disperse phase with inlet velocity of sine functions under different cycles |
为方便讨论,将每个模型生成的前20个液滴的尺寸及生成时间绘制成图 4和图 5。
|
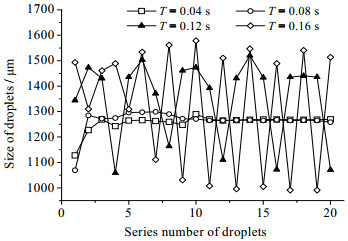
图 4 不同周期条件下生成的前20个液滴的尺寸 Fig.4 Sizes of the first 20 droplets at different inlet velocity cycles |
|
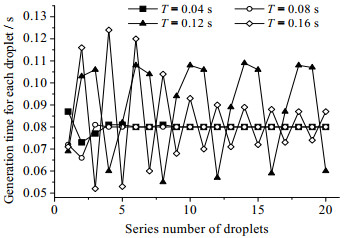
图 5 不同周期条件下前20个液滴的生成时间 Fig.5 Generation times of the first 20 droplets at different inlet velocity cycles |
由图 4可见,正弦函数周期为0.04和0.08 s时,当生成11个液滴后,液滴的尺寸基本不再变化,说明流体流动已经稳定,这时液滴的尺寸均一性较好,且液滴的尺寸约为1242 μm,这与分散相入口流速为0.01 m·s-1条件下得到的液滴尺寸基本一致。正弦函数周期为0.12和0.16 s时,液滴的尺寸呈周期性变化,其中周期为0.12 s时,每个尺寸变化周期内包含4个液滴,而周期为0.16 s时,每个尺寸变化周期内包含2个液滴。
由图 5可见,正弦函数周期为0.04和0.08 s时,当流体流动稳定后,液滴的生成时间均为0.08 s,与分散相入口流速为0.01 m·s-1时得到的液滴生成时间一致。正弦函数周期为0.12和0.16 s时,液滴的生成时间呈周期性变化,其中周期为0.12 s时,每个液滴生成时间的变化周期内包含4个液滴,与图 4中的规律一致;周期为0.16 s时,每个液滴生成时间的变化周期内包含2个液滴,同样与图 4中的规律一致。
从上述分析可以看出,当分散相入口流速正弦函数的周期≤0.08 s(分散相入口流速为0.01 m·s-1时的液滴生成周期)时,分散相入口流速周期的改变对生成液滴的尺寸和生成时间没有太大影响。当分散相入口流速正弦函数的周期大于0.08 s时,正弦函数周期的改变将改变液滴的尺寸,并对液滴尺寸的均一性产生影响,同时还会影响液滴的生成时间。
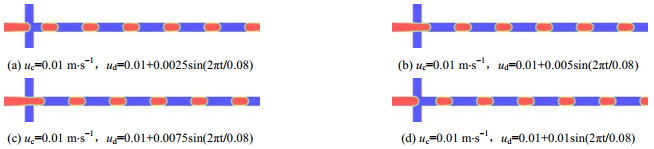
4.2 正弦函数的振幅对液滴生成的影响为探究分散相入口流速为正弦函数变化时,函数振幅对液滴的生成产生的影响,本文采用了周期T=0.08 s,振幅分别为A=0.0025、0.005、0.0075、0.01的正弦函数作为分散相入口流速函数进行数值计算,数值模拟得到的液滴形态如图 6所示。
|
图 6 不同振幅下入口流速为正弦函数时的液滴形态 Fig.6 Droplet morphology of the disperse phase with inlet velocity of sine functions under different amplitudes |
为方便讨论,将每个模型生成的前20个液滴的尺寸及生成时间绘制成图 7和图 8。
|
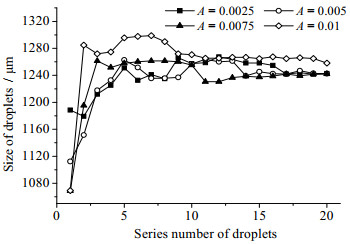
图 7 不同振幅条件下生成的前20个液滴的尺寸 Fig.7 Sizes of the first 20 droplets at different amplitudes |
|
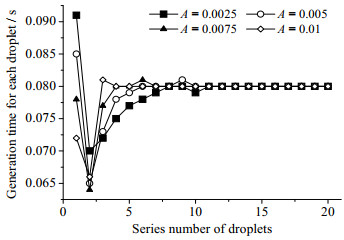
图 8 不同振幅条件下前20个液滴的生成时间 Fig.8 Generation times of the first 20 droplets at different amplitudes |
由图 7可见,正弦函数周期为0.08 s时,在不同振幅下,当流体流动稳定后,液滴的尺寸均一性较好,且与分散相入口流速为0.01 m·s-1时得到的液滴尺寸基本一致。
由图 8可见,当正弦函数周期为0.08 s时,在不同的振幅条件下,流体流动稳定后液滴生成的时间均为0.08 s,与正弦函数周期相同,即与分散相入口流速为0.01 m·s-1时液滴的生成时间一致,值得注意的是,第一个液滴的生成时间以及流体流动达到稳定所用的时间随正弦函数振幅的减小而增大。
上述分析表明,当分散相入口流速正弦函数的周期与定常分散相入口流速条件下液滴生成周期相同时,正弦函数的振幅对液滴的尺寸和生成时间的影响较小。
5 结论本文运用VOF模型,通过UDF导入控制分散相入口流速的函数,数值模拟了十字型微通道中分散相入口流速为正弦函数时液滴的生成过程。本文采用控制变量法引入了多种周期和振幅的正弦函数,分别导入计算模型中。通过分析比较各模型的数值计算结果,可以得出以下结论:
(1) 保持分散相入口流速函数振幅一定,当函数周期小于或等于相应的定常分散相入口流速条件下液滴的生成周期时,液滴生成过程与定常的分散相入口流速基本一致;当函数周期大于定常分散相入口流速条件下液滴的生成周期时,函数对液滴的生成过程影响较大,液滴尺寸和生成时间呈周期性变化。
(2) 保持分散相入口流速函数的周期为定常分散相入口流速条件下液滴的生成周期,当函数的振幅发生改变时,液滴的生成过程与定常分散相入口流速时液滴的生成过程高度一致。但不同的振幅对流体流动到达稳定状态所用的时间有一定的影响,通过对比分析可以看出,正弦函数振幅的越小,流体流动达到稳定状态所用的时间越长。
符号说明:
|
|
| [1] | Parhizkar M, Edirisinghe M, Stride E. Effect of operating conditions and liquid physical properties on the size of monodisperse microbubbles produced in a capillary embedded T-junction device[J]. Microfluidics and Nanofluidics , 2013, 14(5): 797-808. DOI:10.1007/s10404-012-1098-0. |
| [2] | Maan A, Nazir A, Khan M, et al. Microfluidic emulsification in food processing[J]. Journal of Food Engineering , 2015, 147: 1-7. DOI:10.1016/j.jfoodeng.2014.09.021. |
| [3] | Kim S, Lee J. Droplet DNA binding detection on microfluidic flow-focusing[C]. IEEE Sensors, 2015: 1-3. |
| [4] | Cubaud T, Mason T G. Capillary threads and viscous droplets in square microchannels[J]. Physics of Fluids , 2008, 20(5): 501-123. |
| [5] | Costa A L R, Gomes A, Cunha R L. Studies of droplets formation regime and actual flow rate of liquid-liquid flows in flow-focusing microfluidic devices[J]. Experimental Thermal and Fluid Science , 2017, 85: 167-175. DOI:10.1016/j.expthermflusci.2017.03.003. |
| [6] | Van Loo S, Stoukatch S, Kraft M, et al. Droplet formation by squeezing in a microfluidic cross-junction[J]. Microfluidics and Nanofluidics , 2016, 20(10): 1-12. |
| [7] | Cherlo S K, Kariveti S, Pushpavanam S, et al. Experimental and numerical investigations of two-phase (liquid−liquid) flow behavior in rectangular microchannels[J]. Industrial and Engineering Chemistry Research , 2010, 49(2): 893-899. DOI:10.1021/ie900555e. |
| [8] | LIU Jian-pu (刘检朴). The study on the mechanism of droplet generation in flow focusing microchannels (聚焦型微通道内液滴生成的机理研究) [D]. Shanghai (上海): East China University of Science and Technology (华东理工大学), 2015. |
| [9] | Li D, Li X B, Li F, et al. Experimental and numerical study on the droplet formation in a cross-flow microchannel[J]. Journal of Nanoscience and Nanotechnology , 2015, 15(4): 2964-2969. DOI:10.1166/jnn.2015.9651. |
| [10] | Mohammad N, Daulet I, Metin M. Droplet formation in a flow focusing configuration:Effects of viscoelasticity[J]. Physics of Fluids , 2016, 28(12): 123102, 1-13. |
| [11] | WANG Wei-meng (王维萌), CHEN Bin (陈斌). Numerical simulation of W/O micro-droplet generation process in crossing microchannel with VOF method (十字交叉微通道内 W/O 微液滴生成过程的 VOF 模拟) [C]. Multiphase Flow and non-Newtonian Flow and National Symposium on Multiphase and non-Newtonian Flow (多相流与非牛顿流暨全国多相流与非牛顿流学术研讨会), 2012. |
| [12] | Chekifi T, Dennai B, Khelfaoui R. Numerical simulation of droplet breakup, splitting and sorting in a microfluidic device[J]. Fluid Dynamics and Materials Processing , 2015, 11(3): 205-220. |
| [13] | Wu L, Tsutahara M, Kim L S, et al. Three-dimensional lattice Boltzmann simulations of droplet formation in a cross-junction microchannel[J]. International Journal of Multiphase Flow , 2008, 34(9): 852-864. DOI:10.1016/j.ijmultiphaseflow.2008.02.009. |
| [14] | Gupta A, Sbragaglia M, Foard E, et al. Viscoelastic multicomponent fluids in confined flow-focusing devices[C]. AIP Conference Proceedings, 2015, 1648: 865-929. |
| [15] | Castrohernandez E, Kok M P, Versluis M, et al. Study of the geometry in a 3D flow-focusing device[J]. Microfluidics and Nanofluidics , 2016, 20(2): 1-8. |
| [16] | Chen J M, Kuo M C. Generation and control of droplet in cross microchannel flow with a converging-diverging nozzle shaped section[C]. ASME 2010, Biennial Conference on Engineering Systems Design and Analysis, 2010: 347-352. |
| [17] | Gulati S, Vijayakumar K, Good W W, et al. Microdroplet formation in rounded flow-focusing junctions[J]. Microfluidics and Nanofluidics , 2016, 20(1): 1-9. DOI:10.1007/s10404-015-1676-z. |
| [18] | WANG Wei-meng(王维萌), MA Yi-ping(马一萍), CHEN Bin(陈斌). Numerical simulation of droplet generation in crossing micro-channel(十字交叉微通道内微液滴生成过程的数值模拟)[J]. CIESC Journal(化工学报) , 2015, 66(5): 1633-1641. DOI:10.11949/j.issn.0438-1157.20141899. |




