2. 陕西省能源化工过程强化重点实验室, 陕西 西安 710049;
3. 热流科学与工程教育部重点实验室, 陕西 西安 710049
2. Shaanxi Key Laboratory of Energy Chemical Process Intensification, Xi'an 710049, China;
3. Key Laboratory of Thermo-Fluid Science and Engineering, Ministry of Education, Xi'an 710049, China
石油炼制和煤化工等能源化工工艺系统需求大量氢气,随着炼油装置加工高硫、重质油比例的增加和现代煤化工产业的迅猛发展,氢气需求量急剧增加。炼厂中,原油处理量和原油品质、产品质量要求、柴汽比要求、催化剂活性衰减、工艺升级、季节更替和市场价格等内外部因素的变化[1]导致炼厂氢气的需求呈现波动性。
蒸汽甲烷重整装置(steam methane reforming,SMR)是目前炼油厂的主要制氢工艺,占全球氢气供应量的48%[2]。尽管SMR制氢的成本较低,但排放大量温室气体[3]。近年来,为了减少化工生产系统的温室气体排放,提高可再生能源的消纳能力[4],采用可再生能源制氢代替传统化石燃料制氢已成为趋势[5-7]。Al-Subaie等[8]研究了SMR制氢和采用电网电力电解水制氢用于炼油厂的环境影响,阐明了电解水制氢在炼油厂中的减碳潜力。针对工厂中油砂沥青改质的氢气需求和用电需求,Olateju等[9-11]建立了风电场发电和制氢的技术经济模型,确定了最低氢生产成本下系统的容量配置。Walker等[12]分析了电转气(power to gas,PtG)技术为沥青升级装置提供氢气的经济性和环境影响。针对可再生能源发电的间歇性和波动性与化工过程系统氢气需求的协调匹配问题,王靖等[13]研究了电-氢协调储能系统的设计和运行特性。
由于可再生能源的间歇性和波动性以及炼厂氢气需求的波动性,为了满足氢气需求,仅采用可再生能源制氢供应炼厂氢气的系统费用高且可靠性差。在实际应用中,由于气候和天气状况可能无法满足系统的氢气需求,有必要采用可再生能源制氢和氢气公用工程共同满足炼油厂氢气需求,并通过公用工程氢气调整氢气负荷需求特性,辅助平衡可再生能源发电和氢气负荷。
在可再生能源系统中,电力负荷的波动对系统的经济性和系统配置影响很大。Linssen等[14]分析了用户负载曲线对光伏-电池系统的总费用、光伏(photovoltaics,PV)和电池容量配置的影响。Yuan等[15]研究了不同气候条件下建筑物组合引起的多种负荷曲线对分布式能源系统中蓄热系统经济性的影响。Jiang等[16]针对多种类电池储能系统分析了供需曲线变化特性对电池种类选择和容量配置的影响。对于采用可再生能源和氢气公用工程共同供给炼油厂氢气的系统中,氢气负荷波动特性将对系统的经济性和设计特性的产生重要影响。
在基于可再生能源的分布式能源系统中,通常可采用需求侧管理策略调整负荷特性以提高系统的经济性和可靠性[17],通过负荷转移或负荷降低等方式降低负荷峰值以保持发电侧和负荷侧的平衡[18]。在电力系统中,该策略是用户根据用电方式调整用电量和用电时间以适应电价随时间的变化,增强用电负荷需求的灵活性[19]。Xiang等[20]分析了基于价格的需求响应和基于激励的需求响应的并网集成能源系统的经济性和环境效益。需求侧管理是一种提高系统经济性的有效方法之一。同时,对于可再生能源发电侧而言,可以通过电力入网消耗过剩的电量,根据能源系统中供应侧管理和需求侧管理的思想,在可再生能源制氢与波动性氢气负荷耦合系统中,可通过公用工程氢气调整氢气负荷需求特性,并通过电力入网调整发电侧特性。
针对可再生能源制氢与波动性氢气负荷耦合系统,在满足波动氢气负荷需求的前提下,本文提出可再生能源发电入网调整发电侧和通过氢气公用工程调整氢气负荷侧波形的协同调控策略,目的在于提高可再生能源耦合波动性氢气负荷需求的系统经济性,并研究需求侧氢气负荷的波动幅度和周期变化波动等特性对系统经济性和设计特性的影响。
2 系统结构与问题描述图 1为采用可再生能源和氢气公用工程共同供给波动性氢气负荷需求的系统结构。可再生能源侧PV和风机(wind turbines,WT)产生的电用于电解水制氢气。对于可再生能源发电侧,电力可以进入电网、储存在电池(battery energy storage system,BESS),制氢后存贮在氢气储罐1(hydrogen tank,HT1)中,或者弃电;对于氢气负荷侧,可采用可再生能源和氢气公用工程共同供给炼油厂氢气需求,或者使用储罐中的氢气。考虑到氢气公用工程的稳定性要求,需要配置氢气储罐2(hydrogen tank,HT2)。对于上述系统,本文根据炼油厂的氢气需求情况,以系统的总费用最小为目标,获得该系统的设计和操作特性。
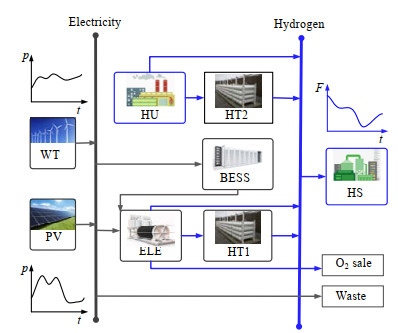
|
图 1 可再生能源和氢气公用工程共同供给炼厂氢气需求的系统结构 Fig.1 Schematic diagram of the coupling system for renewable energy and fluctuating hydrogen demands |
在系统中,发电侧由当地的风光等自然条件决定,负荷侧的氢气需求由炼油厂的氢气系统决定,例如在炼油工艺的实际生产中,由于原油处理量和品质、产品质量要求、柴汽比要求、催化剂活性衰减、工艺升级、季节更替和市场价格等内外部因素的变化,炼油厂的不同加工方案导致其氢气网络操作工况的切换和操作条件的变化,氢气需求呈现波动性。本文通过比较分析典型氢气负荷波形下的系统优化结果,研究负荷侧的氢气波动特性对系统结构和经济性的影响,阐明负荷端氢气波动特性对系统经济性和设计特性的影响规律。
在此基础上,为了提高系统的经济性,本文提出了通过电力入网和氢气公用工程协同调控发电侧和负荷侧波形以降低系统的总费用的策略。在本文系统中,负荷侧的氢气由可再生能源和公用工程氢气共同供给,因此可以考虑在公用工程稳定流率限制的基础上,通过公用工程氢气调节负荷侧的波形,稳定的电力入网作为可再生能源发电过剩量的出口,或通过电力入网调节发电侧和负荷侧的匹配。
3 数学模型 3.1 目标函数针对图 1所示系统,本文以年度化总费用(total annual cost,TAC)最小化为目标,总费用包括系统寿命期间内光伏、风机、电池系统、电解槽和氢气储罐的投资和维护费用以及外部氢气公用工程供氢的费用,系统的收益为副产氧气的销售收益和电力入网的收益。
该系统的年度化总费用包括系统的投资费用和操作费用并减去收益,可表示为
| ${C_{{\rm{total}}}} = {C_{{\rm{inv}}}} + {C_{{\rm{ope}}}} - {C_{{\rm{inc}}}}$ | (1) |
式中:Ctotal为总费用;
该系统的年度化投资费用为在系统寿命期限内系统内各个组件的投资费用转化的年度化费用,系统的操作费用包括系统中各个组件在一年内的维护费用和氢气公用工程供氢费用。
| ${C_{{\rm{inv}}}}{\rm{ = }}\sum\limits_i {{Q^i} \cdot C_{{\rm{cap}}}^i \cdot {\rm{CRF}}} + {C^{{\rm{COM}}}} \cdot {\rm{CRF}}$ | (2) |
| ${C_{{\rm{ope}}}} = {\sum\limits_i^{} {{Q^i} \cdot } _{}}C_{{\rm{mai}}}^i{\rm{ + }}{C_{{{\rm{H}}_{\rm{2}}}}}\sum\limits_{k = 1}^K {f_k^{{\rm{HU}}}} \cdot \Delta t$ | (3) |
| ${C_{{\rm{inc}}}} = {C_{{{\rm{O}}_{\rm{2}}}}}\sum\limits_{k = 1}^K {f_k^{{\rm{ELE, OM}}}} \cdot \Delta t + C_{{\rm{Grid}}}^{}\sum\limits_{k = 1}^K {P_k^{\rm{G}}} \cdot \Delta t$ | (4) |
式中:上标i代表风机(WT)、光伏(PV)、电池(BESS)、电解槽(ELE)或氢气储罐(HT1和HT2)等组件;
| ${\rm CRF} = \frac{{r{{(1 + r)}^{{L^i}}}}}{{{{(1 + r)}^{{L^i}}} - 1}}$ | (5) |
式中:Li为系统中各个组件的寿命;r为利率。
为了评价可再生能源产生氢气在氢气需求中所占的份额,本文定义可再生能源产生的氢气占负荷端氢气需求的比例为可再生能源的渗透率
| $\zeta = \sum\limits_{k = 1}^K {(f_k^{{\rm{ELE, H}}} + f_k^{{\rm{HT1, H}}}} )/\sum\limits_{k = 1}^K {f_k^{\rm{H}}} $ | (6) |
式中:
为了衡量可再生能源发电的入网率,本文定义可再生能源发电进入电网的电量占总发电量的比例为入网率
| $\chi = \sum\limits_{k = 1}^K {P_k^{{\rm{S, G}}}/\sum\limits_{k = 1}^K {P_k^{\rm{S}}} } $ | (7) |
式中:
为了衡量可再生能源发电的弃电率,本文定义可再生能源发电弃掉的电量占总发电量的比例为弃电率
| $\phi = \sum\limits_{k = 1}^K {P_k^{{\rm{S, W}}}/\sum\limits_{k = 1}^K {P_k^{\rm{S}}} } $ | (8) |
式中:
发电侧电力来自风机和光伏发电,满足
| $P_k^{\rm{S}}{\rm{ = }}{a_k} \cdot P_{}^{{\rm{WT}}} + {b_k} \cdot P_{}^{{\rm{PV}}}$ | (9) |
式中:
风机和光伏发电的电力可用于电解水,剩余电力可储存在电池中、供入电网或者直接弃电,即
| $P_k^{\rm{S}} = P_k^{{\rm{S, ELE}}} + P_k^{{\rm{S, BESS}}} + P_k^{{\rm{S, G}}} + P_k^{{\rm{S, W}}} + P_k^{{\rm{S, COM}}}$ | (10) |
式中:
电解槽是将电力转换为氢气和氧气的关键装置。本文选择质子交换膜水解电池(PEMEC)电解制氢工艺,电解槽的输入功率由发电侧风力发电和储能电池系统提供,可表示为
| $P_{k, {\rm{in}}}^{{\rm{ELE}}} = P_k^{{\rm{S, ELE}}}{\eta _{{\rm{ELE}}}} + P_k^{{\rm{BESS, ELE}}}{\eta _{{\rm{ELE}}}}$ | (11) |
式中:
电解槽输出的氢气流率表示为
| $f_k^{{\rm{ELE, H}}} + f_k^{{\rm{ELE, HT1}}} = P_{k, {\rm{in}}}^{{\rm{ELE}}}/{\eta _{\rm e}}$ | (12) |
式中:
根据电解水制氢的化学计量关系,电解水生产1 kg氢气产生8 kg氧气,氧气的流率可表示为
| $f_k^{{\rm{ELE, OM}}} = 8P_{k, {\rm{in}}}^{{\rm{ELE}}}/{\eta _{\rm e}}$ | (13) |
式中:
对于电解槽,其最小运行功率取额定功率的5%,可表示为
| $P_{{\rm{min}}}^{{\rm{ELE}}}\delta _k^{{\rm{ELE}}} \leqslant P_{k, {\rm{in}}}^{{\rm{ELE}}} \leqslant P_{{\rm{max}}}^{{\rm{ELE}}}\delta _k^{{\rm{ELE}}}$ | (14) |
| $5{\rm{\% }}P_{{\rm{rated}}}^{{\rm{ELE}}} - P_{{\rm{max}}}^{{\rm{ELE}}}(1 - \delta _k^{{\rm{ELE}}}) \leqslant P_{k, {\rm{in}}}^{{\rm{ELE}}} \leqslant P_{{\rm{rated}}}^{{\rm{ELE}}}$ | (15) |
式中:
PEMEC制氢气时输出氢气的压力为3 MPa,需要将氢气压缩至20 MPa储存在氢气储罐(HT1)中[22-23],氢气公用工程输出氢气的压力为2.1 MPa,需要将氢气压缩至20 MPa储存在氢气储罐(HT2)中,压缩机的功率可表示为[24]
| $P_k^{{\rm{RE, COM1}}} = \frac{{{c_p}T}}{\eta } \cdot \left[ {{{\left( {\frac{{{p^{{\rm{ELE}}}}}}{{{p^{{\rm{HT}}1}}}}} \right)}^{(\gamma - 1)/\gamma }} - 1} \right] \cdot f_k^{{\rm{ELE, HT1}}}$ | (16) |
| $P_k^{{\rm{HU, COM2}}} = \frac{{{c_p}T}}{\eta } \cdot \left[ {{{\left( {\frac{{{p^{{\rm{HU}}}}}}{{{p^{{\rm{HT2}}}}}}} \right)}^{(\gamma - 1)/\gamma }} - 1} \right] \cdot f_k^{{\rm{HU, HT2}}}$ | (17) |
式中:
为压缩机供电的电力来源可来自可再生能源或者电池。
| $P_k^{{\rm{RE, COM1}}} = P_k^{{\rm{S, COM1}}} + P_k^{{\rm{BESS, COM1}}}$ | (18) |
| $P_k^{{\rm{HU, COM2}}} = P_k^{{\rm{S, COM2}}} + P_k^{{\rm{BESS, COM2}}}$ | (19) |
| $P_k^{{\rm{S, COM}}} = P_k^{{\rm{S, COM1}}} + P_k^{{\rm{S, COM2}}}$ | (20) |
| $P_k^{{\rm{BESS, COM}}}{\rm{ = }}P_k^{{\rm{BESS, COM1}}} + P_k^{{\rm{BESS, COM2}}}$ | (21) |
式中:
压缩机的投资费用可表示为
| $C_k^{{\rm{RE, COM1}}} = ({a^{{\rm{COM}}}} + {b^{{\rm{COM}}}} \cdot P_k^{{\rm{RE, COM1}}}) \times {10^4}$ | (22) |
| $C_k^{{\rm{HU, COM2}}} = ({a^{{\rm{COM}}}} + {b^{{\rm{COM}}}} \cdot P_k^{{\rm{HU, COM2}}}) \times {10^4}$ | (23) |
| $C_{}^{{\rm{RE, COM1}}} \geqslant C_k^{{\rm{RE, COM1}}}$ | (24) |
| $C_{}^{{\rm{HU, COM2}}} \geqslant C_k^{{\rm{HU, COM2}}}$ | (25) |
| $C_{}^{{\rm{COM}}}{\rm{ = }}C_{}^{{\rm{RE, COM1}}} + C_{}^{{\rm{HU, COM2}}}$ | (26) |
式中:
储能系统的相关约束与文献[13]基本相同。唯一区别是本文系统中电池的输出功率包括进入电解槽的功率、进入电网的功率以及进入压缩机的功率,表示为
| $P_{k, {\rm{out}}}^{{\rm{BESS}}} = P_k^{{\rm{BESS, ELE}}} + P_k^{{\rm{BESS, G}}} + P_k^{{\rm{BESS, COM}}}$ | (27) |
式中:
为了满足负荷侧氢气需求,对于第k时间段,由电解水产生的氢气、氢储罐储存的氢气和外部氢气公用工程共同满足氢气需求,表示为
| $f_k^{\rm{H}} = f_k^{{\rm{ELE, H}}} + f_k^{{\rm{HT1, H}}} + f_k^{{\rm{HU, H}}} + f_k^{{\rm{HT2, H}}}$ | (28) |
式中:
氢气公用工程输出的氢气可直接供应负荷需求,也可储存在氢储罐(HT2)中,可表示为
| $f_k^{{\rm{HU}}} = f_k^{{\rm{HU, H}}} + f_k^{{\rm{HU, HT2}}}$ | (29) |
为了稳定公用工程制氢装置的输出流率,避免操作工况的大幅度波动,需针对公用工程的氢气流率加以限制,本文计算的时间尺度是一年,要求氢气公用工程的波动幅度在一年内限制在一定范围内,即
| $(1 - {\alpha ^{{\rm{HU}}}})f_{\rm S}^{{\rm{HU}}} \leqslant f_k^{{\rm{HU}}} \leqslant (1 + {\alpha ^{{\rm{HU}}}})f_{\rm S}^{{\rm{HU}}}$ | (30) |
式中:
对于将运行周期划分多个子周期的系统,也可使氢气公用工程在各个子周期内保持稳定流率,因此氢气公用工程的稳定性约束可以修正为
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1 - {\alpha ^{{\rm{HU}}}}){f_{\rm{S}}}_{, 1}^{{\rm{HU}}} \le f_k^{{\rm{HU}}} \le (1 + {\alpha ^{{\rm{HU}}}}){f_{S, }}_1^{{\rm{HU}}}\;\;\;\;\;\;\;\;\;k \in [1, T]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}(1 - {\alpha ^{{\rm{HU}}}}){f_{\rm{S}}}_{, 2}^{{\rm{HU}}} \le f_k^{{\rm{HU}}} \le (1 + {\alpha ^{{\rm{HU}}}}){f_{\rm{S}}}_{, 2}^{{\rm{HU}}}\;\;\;\;\;\;\;\;\;\;\;k \in [T + 1, 2T]{\rm{ }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;(1 - {\alpha ^{{\rm{HU}}}}){f_{\rm{S}}}_{, 3}^{{\rm{HU}}} \le f_k^{{\rm{HU}}} \le (1 + {\alpha ^{{\rm{HU}}}}){f_{\rm{S}}}_{, 3}^{{\rm{HU}}}\;\;\;\;\;\;\;\;\;\;\;k \in [2T + 1, 3T]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;...\\ \;\;\;\;\;\;\;\;\;\;(1 - {\alpha ^{{\rm{HU}}}}){f_{\rm{S}}}_{, m}^{{\rm{HU}}} \le f_k^{{\rm{HU}}} \le (1 + {\alpha ^{{\rm{HU}}}}){f_{\rm{S}}}_{, m}^{{\rm{HU}}}\;\;\;\;\;\;\;\;\;\;\;\;\;k \in [(m - 1)T + 1, K] \end{array}$ | (31) |
式中:m为所划分的子周期的数目,代表各个子周期内公用工程氢气的稳定流率约束;K为总的时间段;T为每个子周期的时间;T=K/m。该约束表示公用工程氢气需要在各个子周期内分别保持稳定流率,但各子周期内平均流率是独立的。
进入电网的电可直接来自可再生能源发电侧,也可来自电池储能系统,可表示为
| $P_k^{\rm{G}} = P_k^{{\rm{S, G}}} + P_k^{{\rm{BESS, G}}}$ | (32) |
当可再生能源发电系统与电网相连接,并且可以将过剩电量供入电网时,为避免波动性和间歇性的可再生能源发电侧的大幅度波动对电网造成冲击,本文限制在某一区间内入网功率波动,表示为
| $(1 - {\alpha ^{\rm{G}}})P_{\rm{S}}^{\rm{G}} \leqslant P_k^{\rm{G}} \leqslant (1 + {\alpha ^{\rm{G}}})P_{\rm{S}}^{\rm{G}}$ | (33) |
式中:
对于子周期m,电力入网功率稳定性约束可以修正为
| $\begin{array}{l} \ \ \ \ (1 - {\alpha ^{\rm{G}}})P_{{\rm{S}}, 1}^{\rm{G}} \leqslant P_k^{\rm{G}} \leqslant (1 + {\alpha ^{\rm{G}}})P_{{\rm{S}}, 1}^{\rm{G}}{\rm{ }}k \in [1, T] \\ (1 - {\alpha ^{\rm{G}}})P_{{\rm{S}}, 2}^{\rm{G}} \leqslant P_k^{\rm{G}} \leqslant (1 + {\alpha ^{\rm{G}}})P_{{\rm{S}}, 2}^{\rm{G}}{\rm{ }}k \in [T + 1, 2T] \\ (1 - {\alpha ^{\rm{G}}})P_{{\rm{S}}, 3}^{\rm{G}} \leqslant P_k^{\rm{G}} \leqslant (1 + {\alpha ^{\rm{G}}})P_{{\rm{S}}, 3}^{\rm{G}}{\rm{ }}k \in [2T + 1, 3T] \\ \ \ \ \ \ \ \ \ \ \ \ \ ... \\ (1 - {\alpha ^{\rm{G}}})P_{{\rm{S}}, m}^{\rm{G}} \leqslant P_k^{\rm{G}} \leqslant (1 + {\alpha ^{\rm{G}}})P_{{\rm{S}}, m}^{\rm{G}}{\rm{ }}k \in [(m - 1)T + 1, K] \\ \end{array} $ | (34) |
对图 1所示的系统,本文计算分析的基准时间为一年。发电侧数据包括某地风力发电的容量因子[25]和光伏发电的容量因子[26],如图 2所示。该系统的负荷侧为某炼油厂的波动氢气需求,氢气需求变化特性(如变化幅度和周期)为炼油厂中不同加工方案下的典型变化特性。本文根据某炼油厂的平均氢气负荷需求,在保持一年内氢气需求总量恒定的条件下,研究负荷侧波动特性对系统的经济性和设计的影响特性。
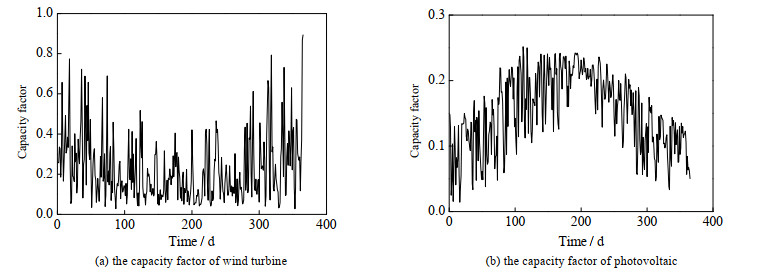
|
图 2 可再生能源发电侧的容量因子 Fig.2 Capacity factors of the renewable energy generation side |
图 3给出典型的负荷侧氢气需求的幅度和周期变化特性。图 3 (a)中为基准负荷和氢气负荷波形,其变化的周期为1,变化幅度为基准负荷的5%、10% 和15%;图 3 (b)为氢气负荷波形的变化幅度为基准负荷的10% 时,变化周期为1、2和3时的情况,其他变化情况以此类推。本文中氢气负荷的平均流率为2 320 kg·h-1。
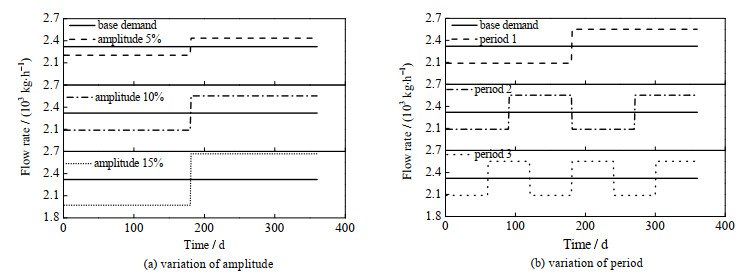
|
图 3 典型的负荷侧氢气需求变化特性 Fig.3 Typical variation characteristics of hydrogen demand |
表 1和2分别给出光伏、风机和电解槽以及储能系统的经济参数和技术参数,系统中氢气公用工程的费用为2.05 $·kg-1,氧气的销售价格是0.16 $·kg-1[27],利率为5%。
|
|
表 1 光伏、风机和电解槽经济参数和技术参数 Table 1 Techno-economic parameters of the WT, PV and electrolyzer |
|
|
表 2 储能系统的经济参数和技术参数 Table 2 Techno-economic parameters of the storage system |
本文的模型方程(式(1)~(34))为混合整数线性规划(MILP)模型。本文采用CPLEX求解器在GAMS软件平台上求解,相对误差为3%,计算机为Intel(R) Xeon(R) i7-8700 CPU@3.20 GHz。
4.2 计算结果的分析与讨论 4.2.1 氢气负荷波形幅度和周期的影响本文分析设定可再生能源发电的弃电率不超过5%,可再生能源的渗透率为80%,在基准场景中,氢气需求为全年平均氢气负荷时,系统的总费用和各组件的容量配置如表 3所示,系统的总费用为6.80×107 $,光伏容量为4.74×105 kW,风电容量为3.62×105 kW,该系统中光伏和风机联合配置的效果最佳。电解槽容量为1.11×105 kW,储能电池的容量为0,氢气储罐HT1的容量为6.73×104 kg。氢气储罐HT2的容量为1.16×105 kg,入网率为26.0%,弃电率达到其上限5%。系统中压缩机的费用为1.20×106 $,占总费用的1.76 %,这说明压缩机的成本相对于总费用而言很小,即使系统中计入氢气储罐储能时压缩机的耗电量和压缩机的成本,配置氢气储罐的经济性依然是优于配置电池的。
|
|
表 3 基准场景中系统的总费用和各组件的容量配置 Table 3 TAC and optimal configuration of the system in the base case |
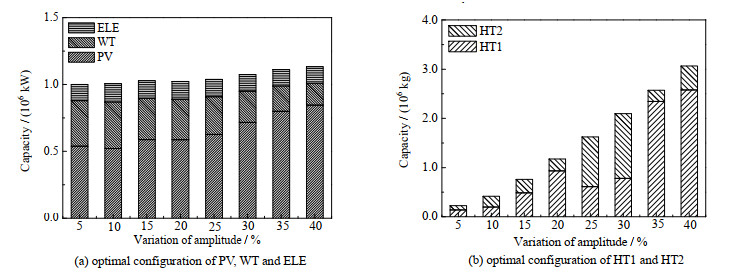
当氢气负荷波动周期为1、波动幅度为5%~40% 时,氢气负荷波动幅度变化对系统经济性和设计特性的影响如图 4、5所示。由图 4可见,随着波动幅度的增大,该系统的总费用增大。当波动幅度为10% 时,系统的总费用为9.09×107$,较基准场景增加了33.6%。这说明当氢气负荷的总量恒定时,氢气负荷波形的幅度变化会对系统的总费用产生很大影响。系统发电的入网率在27%~32%变化。图 5给出各个组件的容量配置情况,由图可见,储能系统容量的增加最为显著,电解槽的容量基本不变,可再生能源侧的总容量基本不变,主要是PV和WT的配置比例发生了变化,随着波动幅度的增加,PV的配置比例增大。这是因为当氢气负荷的波动幅度发生变化时,发电侧和负荷侧的匹配特性发生了变化,发电侧可以通过改变PV和WT的相对容量大小调节发电侧的波形以应对负荷侧波形变化。储能系统容量的显著增加是因为在负荷侧变化幅度大,存在高峰期情况下,为满足高峰期的负荷需求,可再生能源侧的总发电量会增大,这将导致发电侧总发电量远大于负荷侧的总需求量,由于本案例限定了系统的弃电率不超过5%,多余的电量只能以氢气的形式储存在储罐中,造成储能系统容量增大。
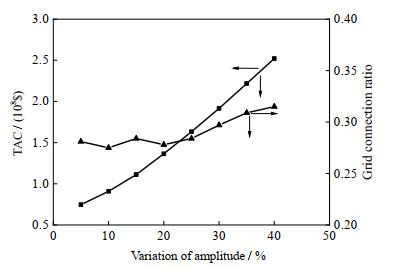
|
图 4 氢气负荷波动的幅度变化对系统经济性的影响 Fig.4 Effects of amplitude variation of hydrogen demand on economy of the system |
|
图 5 氢气负荷波动的幅度变化对系统设计特性的影响 Fig.5 Effects of amplitude variation of the hydrogen demand on the design characteristics of the system |
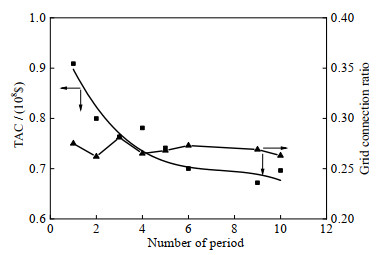
当氢气需求波动幅度为10%、周期数为1~10时,氢气需求波动的周期变化对系统的经济性和设计特性的影响如图 6、7所示,图 6中黑色点为实际数据,曲线为拟合曲线。由图 6可见,总费用随着波动周期的增大,总体趋势呈下降趋势,但在部分周期会有波动,且当周期数大于6时,总费用的降低减缓,周期数为6时的总费用较基准场景增加了2.9%。这说明随着周期数的增加,系统总费用越接近于基准场景。这是因为发电侧和负荷侧的匹配程度是由负荷侧的变化周期和发电侧的容量因子共同决定的。由于发电侧的变化频率高,只有当负荷侧的变化周期数增大,即负荷侧的变化频率也增加时,两者匹配的概率增大,系统的总费用则可能降低。
|
图 6 氢气负荷波动的周期数变化对系统经济性的影响 Fig.6 Effects of period variation of the hydrogen demand on the economy of the system |
|
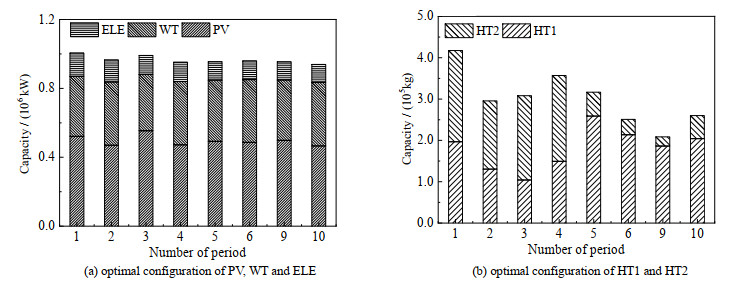
图 7 氢气负荷波动的周期数变化对系统设计特性的影响 Fig.7 Effects of period variation of the hydrogen demand on the design characteristics of the system |
本文中,氢气负荷变化的周期数为6时,氢气负荷的波形是按月变化的,这说明在氢气负荷按月变化可以有效降低系统的总费用,且再增加变化的频率对系统的经济性影响不大。随着周期的变化,系统的入网率在27% 上下波动。系统各个组件的容量变化随周期变化无明显规律,这表明系统的总费用降低是各个组件协调优化的结果。
综上所述,随着氢气负荷波动幅度的增大,系统的总费用和储能系统的容量增加;随着氢气负荷波动周期的增加,系统的总费用降低,且当周期数大于6时,总费用变化幅度较小。
4.2.2 电力入网和氢气公用工程对发电侧和负荷侧波形的调控策略及影响上一节的分析表明,负荷侧的波形幅度和周期变化对系统的经济性和容量配置具有显著影响,且负荷侧为恒定值时系统总费用最低。根据该特点,本文提出通过氢气公用工程调控氢气负荷特性,通过电力入网调控发电侧变化的调控策略,通过发电侧和负荷侧的最优匹配,以达到降低系统总费用的目的。
根据上述特点,在氢气负荷变化时,本文分别通过限制公用工程、电力入网功率在各个子周期内的稳定性,采用不同的调控策略研究系统的经济性。本文的调控策略如下:
(1) 氢气公用工程调节:仅限制氢气公用工程在各个子周期内保持稳定性,用HU表示;
(2) 电力入网调节:仅限制电力入网功率在各个子周期内保持稳定性,用Grid表示;
(3) 氢气公用工程和电力入网同时调节:同时限制氢气公用工程和入网功率在各个子周期内保持稳定性,用HU+Grid表示。
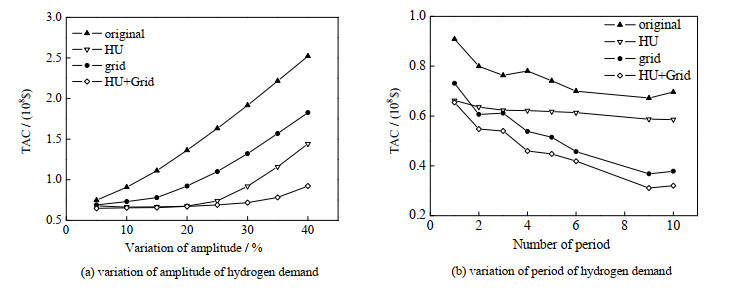
为了便于对比效果,本文将对比采用调控策略与无调控策略下系统的总费用随波动幅度变化,计算结果如图 8所示,图中给出氢气负荷波动幅度和周期数变化时调控策略对系统经济性的影响。
|
图 8 氢气负荷波动幅度和周期数变化时调控策略对系统经济性的影响 Fig.8 Effects of control strategies on system economy with amplitude and period variation of hydrogen demands |
由图 8(a)可见,各种调控策略都可有效降低系统总费用,效果排序为HU+Grid > HU > Grid。例如,在波动幅度为20% 时,HU+Grid、HU和Grid调控策略下总费用较基准场景分别降低了50.8%、50.6% 和32.4%。这是因为在负荷波形的高峰期时,氢气公用工程可削弱负荷波形高峰期的幅度;在负荷波形的低谷期,电力入网可消纳过剩的可再生能源发电量。氢气公用工程和电力入网分别从负荷侧和发电侧出发,通过调节波形,提高了发电侧和负荷侧的匹配程度,从而降低了系统总费用。
当采用氢气公用工程(HU)调节负荷侧波形时,当氢气需求负荷变化幅度小于20% 时,不同幅度下系统的总费用基本相同,约为6.70×107 $;当负荷波形变化幅度大于20% 时,随着波动幅度的增加,系统的总费用增大。这说明当波形变化幅度小于20% 时,氢气公用工程可以有效调节负荷侧波形从而降低系统的总费用;而当变化幅度大于20% 时,氢气公用工程达到了其调节能力的上限,只能在原始波形的基础上削弱幅度,使得调整后的波形较原始波形的费用有所降低。这是因为本文设定可再生能源渗透率为80% 时,氢气公用工程供给负荷占比20%,因而氢气公用工程的调节上限就是幅度为20%,当幅度大于20% 时,氢气公用工程只能在其原有波形基础上削弱幅度,但已无法调整到能与发电侧合理匹配的最优波形。然而,当采用氢气公用工程和电力入网同时调节(HU+Grid)共同调控时,在波动幅度大于20%时总费用的变化依然比较平缓。这说明,当同时采用这两个调控策略时,系统的经济性对于波动幅度的变化的敏感度急剧降低,且受可再生能源渗透率,即公用工程供给比例的影响减弱。
当氢气负荷波动的周期数变化时,不同的调控策略对系统经济性的影响如图 8(b)所示,各种调控策略降低总费用的效果排序为HU+Grid > Grid > HU,且采用氢气公用工程和电力入网同时调节(HU+Grid)的总费用变化趋势与电力入网调节(Grid)下的相同。这是因为当入网功率的稳定性限制松弛之后,由于电力入网售电会产生很大收益,该系统在权衡可再生能源的配置费用和入网收益的基础上,倾向于配置更多的可再生能源用于入网以抵消系统的部分成本。
5 结论针对可再生能源制氢与波动性氢气负荷耦合系统,在满足波动氢气负荷需求的前提下,本文提出可再生能源发电入网调整发电侧和通过氢气公用工程调整氢气负荷侧波形的协同调控策略,目的在于提高可再生能源耦合波动性氢气负荷需求的系统经济性。为了降低系统的总费用,基于氢气负荷需求侧管理方法,本文提出了通过电力入网和氢气公用工程对发电侧和负荷侧波形进行调控的策略,并分析了氢气负荷波动幅度和周期变化时,不同调控策略对系统经济性的影响。
研究表明,负荷侧的氢气波形幅度和周期变化对系统的经济性和容量配置具有显著影响。随着氢气负荷侧波动幅度的增大,系统的总费用增大。在本文案例中,当氢气负荷波动幅度为10% 时,总费用较基准场景增加了33.6%。随着氢气需求波动周期的增加,总费用总体趋势减小,但在部分周期下会有波动。当氢气负荷侧波动的周期数为1、波动幅度为20% 时,氢气公用工程和电力入网同时调节(HU+Grid)、氢气公用工程调节(HU)和电力入网调节(Grid)调控策略下的系统总费用较未施加调控策略的系统分别降低了50.8%、50.6% 和32.4%。这表明氢气公用工程和电力入网的调控策略可以有效降低系统的总费用。当波动幅度变化时,同时采用氢气公用工程和电力入网同时调节的调控策略时,系统的经济性对于波动幅度变化的敏感度降低,且受可再生能源渗透率的影响减弱。本文根据氢气负荷典型的波形变化分析了典型波形变化对系统优化的影响和采用调控策略的有效性。在实际中,氢气负荷的变化特性较复杂,如何根据实际波形变化特性对需求侧进行有效管理以提高耦合系统的经济性,值得深入研究。
| [1] |
LIANG X, KANG L, LIU Y. The flexible design for optimization and debottlenecking of multiperiod hydrogen networks[J]. Industrial & Engineering Chemistry Research, 2016, 55(9): 2574-2583. |
| [2] |
LEMUS R G, MART NEZ DUART J M. Updated hydrogen production costs and parities for conventional and renewable technologies[J]. International Journal of Hydrogen Energy, 2010, 35(9): 3929-3936. DOI:10.1016/j.ijhydene.2010.02.034 |
| [3] |
ACAR C, DINCER I. Comparative assessment of hydrogen production methods from renewable and non-renewable sources[J]. International Journal of Hydrogen Energy, 2014, 39(1): 1-12. DOI:10.1016/j.ijhydene.2013.10.060 |
| [4] |
ACAR C, DINCER I. Review and evaluation of hydrogen production options for better environment[J]. Journal of Cleaner Production, 2019, 218: 835-849. DOI:10.1016/j.jclepro.2019.02.046 |
| [5] |
FONSECA J D, CAMARGO M, COMMENGE J M, et al. Trends in design of distributed energy systems using hydrogen as energy vector: a systematic literature review[J]. International Journal of Hydrogen Energy, 2019, 44(19): 9486-9504. DOI:10.1016/j.ijhydene.2018.09.177 |
| [6] |
PARRA D, VALVERDE L, PINO F J, et al. A review on the role, cost and value of hydrogen energy systems for deep decarbonisation[J]. Renewable and Sustainable Energy Reviews, 2019, 101: 279-294. DOI:10.1016/j.rser.2018.11.010 |
| [7] |
MAGGIO G, NICITA A, SQUADRITO G. How the hydrogen production from RES could change energy and fuel markets: A review of recent literature[J]. International Journal of Hydrogen Energy, 2019, 44(23): 11371-11384. DOI:10.1016/j.ijhydene.2019.03.121 |
| [8] |
AL-SUBAIE A, MAROUFMASHAT A, ELKAMEL A, et al. Presenting the implementation of power-to-gas to an oil refinery as a way to reduce carbon intensity of petroleum fuels[J]. International Journal of Hydrogen Energy, 2017, 42(30): 19376-19388. DOI:10.1016/j.ijhydene.2017.06.067 |
| [9] |
OLATEJU B, MONDS J, KUMAR A. Large scale hydrogen production from wind energy for the upgrading of bitumen from oil sands[J]. Applied Energy, 2014, 118: 48-56. DOI:10.1016/j.apenergy.2013.12.013 |
| [10] |
OLATEJU B, KUMAR A. A techno-economic assessment of hydrogen production from hydropower in Western Canada for the upgrading of bitumen from oil sands[J]. Energy, 2016, 115: 604-614. DOI:10.1016/j.energy.2016.08.101 |
| [11] |
OLATEJU B, KUMAR A, SECANELL M. A techno-economic assessment of large scale wind-hydrogen production with energy storage in Western Canada[J]. International Journal of Hydrogen Energy, 2016, 41(21): 8755-8776. DOI:10.1016/j.ijhydene.2016.03.177 |
| [12] |
WALKER S, MUKHERJEE U, FOWLER M, et al. Implementing power-to-gas to provide green hydrogen to a bitumen upgrader the minimum amount of emissions[J]. International Journal of Energy Research, 2016, 40(14): 1925-1934. DOI:10.1002/er.3557 |
| [13] |
王靖, 康丽霞, 刘永忠. 化工系统消纳可再生能源的电-氢协调储能系统优化设计[J]. 化工学报, 2020, 71(3): 1131-1142. WANG J, KANG L X, LIU Y Z. Optimal design of electricity-hydrogen energy storage systems for renewable energy penetrating into chemical process systems[J]. CIESC Journal, 2020, 71(3): 1131-1142. |
| [14] |
LINSSEN J, STENZEL P, FLEER J. Techno-economic analysis of photovoltaic battery systems and the influence of different consumer load profiles[J]. Applied Energy, 2017, 185: 2019-2025. DOI:10.1016/j.apenergy.2015.11.088 |
| [15] |
YUAN J, CUI C, XIAO Z, et al. Performance analysis of thermal energy storage in distributed energy system under different load profiles[J]. Energy Conversion and Management, 2020, 208: 112596. DOI:10.1016/j.enconman.2020.112596 |
| [16] |
JIANG Y, KANG L, LIU Y. Optimal configuration of battery energy storage system with multiple types of batteries based on supply-demand characteristics[J]. Energy, 2020, 206: 118093. DOI:10.1016/j.energy.2020.118093 |
| [17] |
SHARIATZADEH F, MANDAL P, SRIVASTAVA A K. Demand response for sustainable energy systems: A review, application and implementation strategy[J]. Renewable and Sustainable Energy Reviews, 2015, 45: 343-350. DOI:10.1016/j.rser.2015.01.062 |
| [18] |
WANG J, ZHONG H, MA Z, et al. Review and prospect of integrated demand response in the multi-energy system[J]. Applied Energy, 2017, 202: 772-782. DOI:10.1016/j.apenergy.2017.05.150 |
| [19] |
JORDEHI A R. Optimisation of demand response in electric power systems, A review[J]. Renewable and Sustainable Energy Reviews, 2019, 103: 308-319. DOI:10.1016/j.rser.2018.12.054 |
| [20] |
XIANG Y, CAI H, GU C, et al. Cost-benefit analysis of integrated energy system planning considering demand response[J]. Energy, 2020, 192: 116632. DOI:10.1016/j.energy.2019.116632 |
| [21] |
NICITA A, MAGGIO G, ANDALORO A P F, et al. Green hydrogen as feedstock: Financial analysis of a photovoltaic-powered electrolysis plant[J]. International Journal of Hydrogen Energy, 2020, 45(20): 11395-11408. DOI:10.1016/j.ijhydene.2020.02.062 |
| [22] |
PALYS M J, DAOUTIDIS P. Using hydrogen and ammonia for renewable energy storage: A geographically comprehensive techno-economic study[J]. Computers & Chemical Engineering, 2020, 136: 106785. |
| [23] |
VAN DER ROEST E, SNIP L, FENS T, et al. Introducing Power-to-H3: Combining renewable electricity with heat, water and hydrogen production and storage in a neighbourhood[J]. Applied Energy, 2020, 257: 114024. DOI:10.1016/j.apenergy.2019.114024 |
| [24] |
WU S, LIU G, YU Z, et al. Optimization of hydrogen networks with constraints on hydrogen concentration and pure hydrogen load considered[J]. Chemical Engineering Research and Design, 2012, 90(9): 1208-1220. DOI:10.1016/j.cherd.2011.12.015 |
| [25] |
STAFFELL I, PFENNINGER S. Using bias-corrected reanalysis to simulate current and future wind power output[J]. Energy, 2016, 114: 1224-1239. DOI:10.1016/j.energy.2016.08.068 |
| [26] |
PFENNINGER S, STAFFELL I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data[J]. Energy, 2016, 114: 1251-1265. DOI:10.1016/j.energy.2016.08.060 |
| [27] |
RIVAROLO M, BELLOTTI D, MAGISTRI L, et al. Feasibility study of methanol production from different renewable sources and thermo-economic analysis[J]. International Journal of Hydrogen Energy, 2016, 41(4): 2105-2116. DOI:10.1016/j.ijhydene.2015.12.128 |
| [28] |
KIM H, CHEON H, AHN Y H, et al. Uncertainty quantification and scenario generation of future solar photovoltaic price for use in energy system models[J]. Energy, 2019, 168: 370-379. DOI:10.1016/j.energy.2018.11.075 |
| [29] |
YU Y, LI H, CHE Y, et al. The price evolution of wind turbines in China: A study based on the modified multi-factor learning curve[J]. Renewable Energy, 2017, 103: 522-536. DOI:10.1016/j.renene.2016.11.056 |
| [30] |
COPPITTERS D, DE PAEPE W, CONTINO F. Surrogate-assisted robust design optimization and global sensitivity analysis of a directly coupled photovoltaic-electrolyzer system under techno-economic uncertainty[J]. Applied Energy, 2019, 248: 310-320. DOI:10.1016/j.apenergy.2019.04.101 |
| [31] |
BUTTLER A, SPLIETHOFF H. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review[J]. Renewable and Sustainable Energy Reviews, 2018, 82: 2440-2454. DOI:10.1016/j.rser.2017.09.003 |
| [32] |
GABRIELLI P, GAZZANI M, MARTELLI E, et al. Optimal design of multi-energy systems with seasonal storage[J]. Applied Energy, 2018, 219: 408-424. DOI:10.1016/j.apenergy.2017.07.142 |
| [33] |
KHIAREDDINE A, BEN SALAH C, REKIOUA D, et al. Sizing methodology for hybrid photovoltaic / wind / hydrogen / battery integrated to energy management strategy for pumping system[J]. Energy, 2018, 153: 743-762. DOI:10.1016/j.energy.2018.04.073 |
| [34] |
MARIAUD A, ACHA S, EKINS-DAUKES N, et al. Integrated optimisation of photovoltaic and battery storage systems for UK commercial buildings[J]. Applied Energy, 2017, 199: 466-478. DOI:10.1016/j.apenergy.2017.04.067 |
| [35] |
ZAKERI B, SYRI S. Electrical energy storage systems: A comparative life cycle cost analysis[J]. Renewable and Sustainable Energy Reviews, 2015, 42: 569-596. DOI:10.1016/j.rser.2014.10.011 |




