燃烧炉是整个克劳斯工艺的关键设备,其硫的转化量占整个工艺的70%左右[1]。在燃烧炉内,酸气中的硫化氢与空气中的氧气发生两步克劳斯主反应(2H2S+3O2→2SO2+2H2O和4H2S+2SO2⇋3S2+4H2O),而后将反应过后的气体通过废热锅炉进行能量回收[2]。因此,对燃烧炉的改进是优化克劳斯工艺的重要一环。为了提高和稳定炉内温度、加强炉内气体的混合、反应和延长气体的停留时间,从而增大硫的产率,通常会在燃烧炉内设置扼流圈、花墙等结构。这些结构都是通过改变燃烧炉内部流场,来调控影响燃烧炉混合反应的重要参量[3],如停留时间、温度和湍流强度等,进而提升硫的产率。
传统形式花墙结构力学稳定性较差,经常发生坍塌的状况,而且不利于气体的混合[4-5]。Blasch公司开发了一种安装简单的HexWall花墙,这种花墙通过榫卯结构连接,增大了其稳定性而且更换方便。图 1为HexWall花墙的一种改进形式VectorWall花墙。这种花墙是在HexWall花墙的基础上安装导流装置,使气体通过花墙之后形成漩涡流,进一步加强混合以及延长气体的停留时间。然而现有VectorWall花墙结构也存在一些问题,由于通过导流孔后气体沿轴线方向速度分量偏大,而切线方向速度分量偏小,这就导致了气体在有限的空间内回环的圈数较少,因此现有的导流方式不能充分利用燃烧炉的内部空间。对此,本文基于现役燃烧炉进行数值模拟,分析讨论扼流圈结构燃烧炉、VectorWall花墙结构燃烧炉以及改进花墙结构燃烧炉的模拟结果,探究改进花墙结构对燃烧炉的流动、传热和反应速率的影响和改进花墙结构的优势所在。

|
图 1 VectorWall花墙结构 Fig.1 Structure of VectorWall |
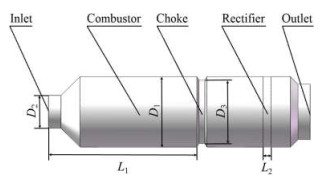
图 2为扼流圈结构燃烧炉模型。燃烧炉的内径D1为3000 mm,入口直径D2为1470 mm,扼流圈直径D3为2700 mm,扼流圈结构距离入口L1为6257 mm。同时,为了使燃烧炉内的流体平稳流出,在燃烧炉出口前端设置有宽度L2为340 mm的整流装置。
|
图 2 扼流圈结构燃烧炉模型 Fig.2 Schematic diagram of a furnace with choke |
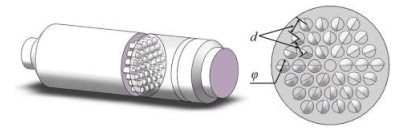
为了得到有效的对比,将燃烧炉中扼流圈的相同位置替换为Vectorwall花墙,如图 3所示,其他尺寸保持与现役燃烧炉完全一致。其中Vectorwall花墙开孔直径φ为300 mm,孔间距d为400 mm,开孔数为37个,正六边形排列。孔上方带有半球形导流装置,导流方向为逆时针方向。
|
图 3 VertorWall花墙结构燃烧炉 Fig.3 Schematic diagram of a furnace with VectorWall |
分析花墙结构缺陷,本文对燃烧炉的花墙结构提出两点改进。
(1) 适当提前花墙相对于燃烧炉的位置,使其接近入口处,增大气体旋流的范围。
(2) 将花墙上的导流孔板延长,缩小通过花墙后气体射出方向与花墙之间的夹角,从而使气体可以绕燃烧炉内产生多次旋流、进一步提升时空利用率。
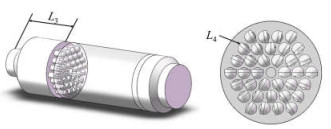
图 4是改进后的燃烧炉模型。花墙结构设置在距入口L3为3.3 m处,花墙上的导流孔板延长L4为100 mm。
|
图 4 改进花墙结构改燃烧炉模型 Fig.4 Schematic diagram of a furnace with improved VectorWall |
对于燃烧炉模型进行分区域网格划分,主体采用六面体结构网格划分,复杂的花墙结构采用四面体网格。扼流圈结构燃烧炉的网格质量在0.7以上,而另外两种具有复杂花墙结构燃烧炉的网格质量也在0.3以上。考虑到燃烧炉内部流场分布梯度的不同,用不同的网格疏密程度进行划分,对于近壁区域的网格进行加密处理。分别将三种模型划分成不同的网格数量,进行网格无关性验证。计算精度随网格数增加而提升,综合考虑计算精度及计算成本,最终确定三种结构燃烧炉的网格数分别为766064、1006652、990545。通过合理的网格划分,很大程度上减少了网格数量,缩减了计算时间,提高了计算精度[6]。
2.2 数学模型由于反应温度很高,燃烧炉内的气体可以假设为理想气体[7]。并且由于气体流速较高,在流动过程中存在的任何扰动都会导致高强度的湍流,所以湍流模型选用realizablek-ε模型[8]。realizable k-ε模型在计算燃烧炉内旋转流时更符合实际情况。其控制方程可参考文献[9-10]。
在组分运输模型中,考虑了5个燃烧炉内的关键反应[11-14],如表 1所示。式中,r为反应速率,Af为正反应指前因子,Eaf为正反应活化能,Ar为逆反应指前因子,Ear为逆反应活化能,R为气体常数,T为温度,P为气体分压。
|
|
表 1 燃烧炉内反应及其反应速率 Table 1 Reactions in the furnace and reaction rate equations |
燃烧炉入口为酸气和空气混合进料,具体成分组成如表 2所示。入口气体的总质量流量为9.17 kg·s-1,流速约为12 m·s-1。利用式(1)计算出入口处湍流强度[15]为3.4%。
| $ I{\rm{ = }}0.16R{e^{ - 1/8}} $ | (1) |
|
|
表 2 入口气体组分 Table 2 Inlet gas compositions |
式中,I为湍流强度,Re = ρvd/μ为雷诺数,v为流速,d为特征长度,μ为动力黏度,ρ为密度。出口为流体充分发展边界条件,壁面采用无滑移边界条件。在传热方面,假设所有的热量都是通过化学反应产生的,并且壁面假设为绝热条件。因此,可以认为所有的反应热都是通过对流流失[16-17]。此外,忽略内部的辐射热交换。
利用有限体积法对上述控制方程进行稳态求解;采用SIMPLEC算法求解离散方程组的压力和速度耦合;动量方程采用QUICK格式进行离散,其他方程均采用二阶迎风格式离散;能量收敛残差为10-6,其余变量收敛残差为10-3[18]。
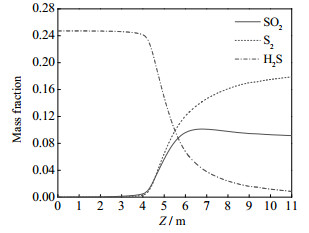
3 结果分析与讨论 3.1 扼流圈结构燃烧炉 3.1.1 组分浓度场图 5给出了扼流圈结构燃烧炉沿轴线方向H2S、SO2、S2的质量分数变化趋势。从图中可以看到,随着反应的进行,H2S的质量分数在逐渐降低,S2的质量分数在逐渐增大,而SO2的质量分数则先增大,而后略微降低。这是由于燃烧炉内的两个主要化学反应的作用:H2S和O2反应生成SO2,使SO2质量分数增大;而生成的SO2和H2S进一步反应生成S2,进而造成SO2质量分数略微降低。另外,距燃烧炉入口8 m左右,燃烧炉内的主要反应基本完成,后段燃烧炉内各物质质量分数改变较小。分析曲线变化趋势可以看到,在燃烧炉4~6 m这段区域内,炉内反应最为剧烈。然而,扼流圈结构设置在距燃烧炉入口6.3 m处。因此,现役燃烧炉中扼流圈的位置是其不能发挥重要作用的原因之一。同样也证明了将花墙位置前提的必要性。
|
图 5 沿轴线方向各组分质量分数变化 Fig.5 Axial profiles of mass fraction of different components |
扼流圈结构燃烧炉出口各物质的质量分数如表 3所示。与现役燃烧炉的实际运行数据做对比,发现H2S和SO2吻合程度不是特别好,主要原因是在实际中,燃烧炉内反应繁多复杂,这其中就包括一些杂质燃烧而消耗氧气的反应。本文为简化模型仅考虑燃烧炉内的5个主要反应,忽略掉了一些杂质的燃烧反应。这导致会有多余的O2和H2S反应生成SO2,使H2S的模拟结果偏低,而SO2的模拟结果偏高。其他模拟结果与现场数据吻合,单质硫的出口质量分数基本一致,验证了计算模型的正确性。
|
|
表 3 出口物质质量分数对比 Table 3 Mass fractions of outlet components |
图 6是三种结构燃烧炉内的温度分布云图。由于扼流圈结构和花墙结构燃烧炉中扼流圈和花墙的位置比较靠后,而在燃烧炉前半部分,温度场就已经基本达到分布均匀。因此这两种结构对温度场的作用不明显。然而,可以看到改进花墙结构由于将花墙位置提前,对温度场作用效果十分明显,加速了气体的混合、反应,使温度场能够更快的达到最高温并保持稳定。
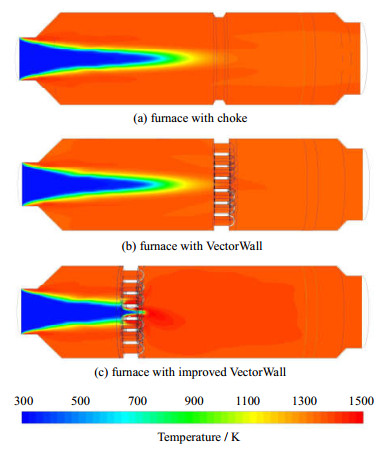
|
图 6 三种结构燃烧炉温度分布 Fig.6 Temperature distribution in the three furnaces |
图 7为三种结构燃烧炉沿轴线方向温度变化曲线。花墙结构与扼流圈结构相比,温度在稍微靠前的位置开始逐渐上升,并且花墙结构燃烧炉内的最高温要高于扼流圈结构的最高温,这体现了花墙结构对于温度场的优势效果;改进花墙结构燃烧炉将花墙位置提前,使花墙能够充分发挥其作用,由图 7温度变化曲线可见,在升温阶段,改进花墙结构温度变化曲线斜率最大,说明炉膛温度快速提升,并且在距燃烧炉入口4 m处就已经达到了最高温度。与之前的两种结构相比,炉膛达到最高温并且稳定的区域增大了3 m。另一方面,改进花墙结构燃烧炉最终稳定的炉膛温度也要高于前两种结构,温度提升了23 K。
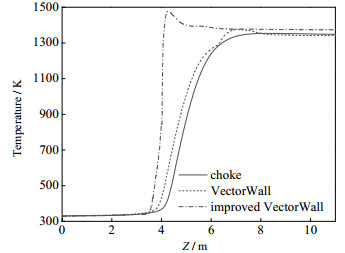
|
图 7 三种结构燃烧炉沿轴线方向温度变化 Fig.7 Axial temperature profiles of these three furnaces |
图 8给出了三种结构燃烧炉内流体的流动迹线及流动时间分布情况。扼流圈结构燃烧炉内气体的平均停留时间为1.4 s,可以清楚地看到,由于扼流圈的作用,燃烧炉内的气体在入口与扼流圈之间产生环流,使气体在燃烧炉内的停留时间有所增加,环流气体的停留时间达到了10 s以上。与此同时,也可以看到扼流圈结构的一些局限性:扼流圈结构仅会在局部产生环流,增大部分气体的停留时间。因此,扼流圈结构对于燃烧炉整体作用效果不明显,不能充分利用燃烧炉的空间;类似于扼流圈结构燃烧炉,VectorWall花墙结构燃烧炉中的气体在入口与花墙之间也产生环流,有效增大部分气体的停留时间。除此之外,可以清楚的看到花墙对气体的导流作用,气体在通过花墙后形成涡旋流旋转前进,加强了对近壁区域的扰动和气体的混合效果,同时也延长了气体的停留时间。但由于花墙位置比较靠后,所以花墙的作用范围仅在花墙与整流装置之间的小部分区域内,使花墙不能充分发挥其优势作用;改进花墙结构将花墙的位置提前,气体旋流的范围较改进前相比增大了3 m,促进了湍流和气体混合效果。另一方面,由于导流孔板的延长,气体旋流方向更倾向于切线方向,使气体在有限的空间内旋流的圈数增多,因此增大了气体的停留时间。
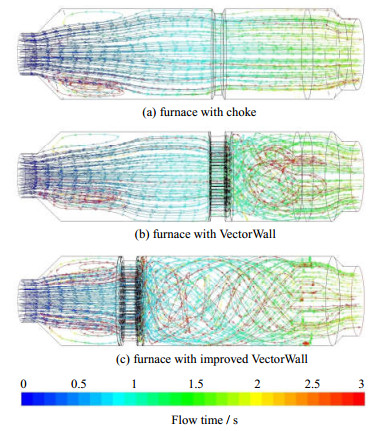
|
图 8 三种结构燃烧炉内流体流动迹线及流动时间 Fig.8 Path lines and flow times of fluids in the three furnaces |
为了更清楚地分析气体通过三种结构燃烧炉的停留时间和混合情况,下文采用脉冲注入法[19]对三种燃烧炉气体的停留时间分布进行模拟测定,分析其流动混合情况。分别在三种结构燃烧炉内先通入氮气,当气体达到定态流动后,在0.1 s内,通入氧气,并保持入口流量不变,然后分析出口氧气的流量随时间的变化。图 9给出了氧气在三种不同结构燃烧炉中的停留时间分布的概率密度曲线,即E(t)。
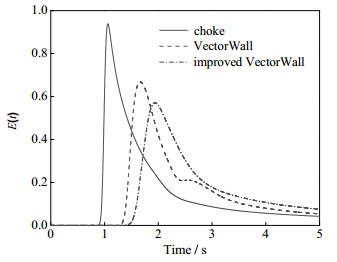
|
图 9 氧气停留时间分布的概率密度 Fig.9 Probability density of oxygen residence time |
下文将用数学期望和方差,两种重要的统计学特征值来分析图像。
(1) 数学期望
| $ {t_{\rm{m}}} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over t} = \frac{{\int_0^\infty {tE{\rm{(}}t){\rm{d}}t} }}{{\int_0^\infty {E{\rm{(}}t){\rm{d}}t} }} = \int_0^\infty {tE{\rm{(}}t){\rm{d}}t} $ | (2) |
(2) 方差σt2又称离散度,用来体现随机变量与其均值的偏离程度。可见方差是对停留时间分布离散程度的度量,σt2越大,越接近全混流;σt2越小,越接近平推流[19]。
| $ {\sigma _t}^2 = \frac{{\int_0^\infty {{{(t - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over t} )}^2}E(t){\rm{d}}t} }}{{\int_0^\infty {E(t){\rm{d}}t} }} = \int_0^\infty {{t^2}E(t){\rm{d}}t} - {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over t} ^2} $ | (3) |
利用式(2)和(3)计算出图 9中曲线数字特征值,具体计算值如表 4所示。结合图像及计算结果进行分析:改进花墙结构燃烧炉的概率密度曲线出峰最晚,说明其气体平均停留时间最大。花墙结构与扼流圈结构相比,平均停留时间由2.14 s提升至2.89 s,而改进花墙结构燃烧炉使气体的停留时间又有了增加,平均停留时间增大到3.49 s;扼流圈结构、花墙结构与改进花墙结构三种结构的概率密度曲线的峰值依次降低,而拖尾依次增大,说明数据偏离中心区域程度也依次增大。表 4给出了三种结构燃烧炉氧气停留时间概率密度曲线的方差计算值,扼流圈结构、花墙结构、改进花墙结构三种结构的方差依次增大。由于σt2越大,越接近全混流,说明花墙结构燃烧炉的混合情况更好,并且改进花墙结构使燃烧炉内部的混合情况进一步加强。
|
|
表 4 数字特征值 Table 4 Numerical characteristic values |
如表 5所示为三种结构燃烧炉出口数据的对比。从表中可以看到花墙结构燃烧炉中SO2出口的质量流量较扼流圈结构燃烧炉相比有所降低,而S2的质量流量有少量增大,从1.702 kg·s-1增大至1.713 kg·s-1,增大了1%。这是由于采用花墙结构使燃烧炉内气体加强了混合,增大了气体的停留时间,提升了时空利用率,使克劳斯反应的第二步反应进行的更加充分,从而增大了硫的产率;改进花墙结构燃烧炉中H2S,SO2出口的质量流量较改进前相比有所降低,S2的质量流量有较大的提升,从1.713 kg·s-1增大至1.843 kg·s-1,增大了7.6%,按照这种效率每天可以多回收12吨以上的单质硫。这是由于改进花墙结构加速燃烧炉升温过程,并且使炉膛稳定在更高的温度;另一方面,其导流方式使燃烧炉内气体进一步加强了混合效果,增大了气体的停留时间,提升了时空利用率。可以看到改进花墙结构对于影响燃烧炉混合反应的重要参量(停留时间、温度和湍流强度)都有积极的影响,因此提升了硫的产率。
|
|
表 5 三种结构燃烧炉出口组分质量流量对比 Table 5 Mass flow rates of outlet components in the three furnaces |
通过将三种不同结构燃烧炉进行数值模拟,对比现役燃烧炉运行数据,本文探究了花墙结构较扼流圈结构相比的优势,并提出了花墙结构的改进方案,得到如下结论:
(1) 扼流圈结构燃烧炉数值模拟结果与现役燃烧炉运行数据基本吻合,验证了计算模型的正确性。
(2) 花墙结构较扼流圈结构相比,加强了气体的混合效果,使气体在燃烧炉内的停留时间延长,使硫的产率增大了1%。
(3) 改进花墙结构燃烧炉在提升并稳定炉膛温度、加强气体混合效果、增大气体停留时间上具有明显的作用。炉膛温度稳定区域在轴线方向延长了3 m,炉膛温度提升了23 K,并且使气体平均停留时间进一步延长,硫的产率进一步提升7.6%。
| [1] | CHANG Hong-gang(常宏岗), WU Chang(吴昌), CHEN Chang-jie(陈昌介), et al. Analysis of gases mixing and structure optimization of Claus furnace(硫磺回收燃烧炉气体混合效果分析及其结构优化)[J]. Natural Gas Industry(天然气工业), 2010, 30(12): 84-89. |
| [2] | CHEN Chang-jie(陈昌介), GAO Yan-nan(高艳楠), CHANG Hong-gang(常宏岗), et al. Research and analysis of MCRC sulfur recovery process(MCRC硫磺回收工艺研究与分析)[J]. Chemical Engineering(化学工程), 2011, 39(3): 72-75. DOI:10.3969/j.issn.1005-9954.2011.03.018. |
| [3] | WANG Wei(王伟), ZHANG Lian-qiang(张联强), LI Yan-ping(李延萍), et al. The furnace and burner of sulfur recovery unit(硫磺回收装置热反应炉及燃烧器)[J]. Petroleum Refinery Engineering(炼油技术与工程), 2008, 38(1): 37-39. DOI:10.3969/j.issn.1002-106X.2008.01.010. |
| [4] | ZHANG Xiao-hua(张晓华), YU Yan-qiu(于艳秋). Problem analysis and remodel of large scale Claus furnace(特大型克劳斯反应炉运行问题分析及改造)[J]. Petroleum Refinery Engineering(炼油技术与工程), 2016, 46(3): 40-44. DOI:10.3969/j.issn.1002-106X.2016.03.010. |
| [5] | XIA Yu-fang(夏毓芳). The improved design of sour gas burning furnace for sulfur recovery unit(硫磺回收装置酸性气燃烧炉的设计改进)[J]. Sulphuric Acid Industry(硫酸工业), 2011(3): 37-40. DOI:10.3969/j.issn.1002-1507.2011.03.011. |
| [6] | JIN Xiang-hong(金向红), JIN You-hai(金有海), WANG Jian-jun(王建军), et al. Numerical and experimental study on the improved inlet geometric construction of gas exhaust pipe in gas-liquid cyclone separator(改进气液旋流器排气管结构的实验及CFD模拟研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2011, 25(2): 205-211. DOI:10.3969/j.issn.1003-9015.2011.02.005. |
| [7] | Manenti F, Papasidero D, Bozzano G, et al. Model-based optimization of sulfur recovery units[J]. Computers & Chemical Engineering, 2014, 66: 244-251. |
| [8] | AI Zhi-jiu(艾志久), JIANG Jing(蒋静), WU Chang(吴昌), et al. Numerical simulation of combustion field in the furnace(炉内燃烧场数值模拟研究)[J]. Journal of Southwest Petroleum University(Science & Technology Edition)(西南石油大学学报(自然科学版)), 2011, 33(3): 165-168. DOI:10.3863/j.issn.1674-5086.2011.03.030. |
| [9] | ZHOU Jun-chao(周俊超), CHE Yuan-yuan(车圆圆), WU Ke-jun(吴可君), et al. Design optimization of the spatial arrangement of coil in strongly exothermic tank reactor based on CFD simulations(基于CFD模拟的强放热反应釜盘管空间排布的优化设计)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2015, 29(1): 27-34. DOI:10.3969/j.issn.1003-9015.2015.01.004. |
| [10] | Bo S, Ma X, Lan Z, et al. Numerical simulation on the falling film absorption process in a counter-flow absorber[J]. Chemical Engineering Journal, 2010, 156(3): 607-612. DOI:10.1016/j.cej.2009.04.066. |
| [11] | Zarei S, Ganji H, Sadi M, et al. Kinetic modeling and optimization of Claus reaction furnace[J]. Journal of Natural Gas Science & Engineering, 2016, 31: 747-757. |
| [12] | Kelly A H. Kinetic modelling of key reactions in the modified Claus plant front end furnace[D]. Calgary: University of Calgary, 1998. |
| [13] | Ghahraloud H, Farsi M, Rahimpour M R. Modeling and optimization of an industrial Claus process:thermal and catalytic section[J]. Journal of the Taiwan Institute of Chemical Engineers, 2017, 76: 1-9. DOI:10.1016/j.jtice.2017.03.005. |
| [14] | Zhou C, Sendt K, Haynes B S. Experimental and kinetic modelling study of H2S oxidation[J]. Proceedings of the Combustion Institute, 2013, 34(1): 625-632. DOI:10.1016/j.proci.2012.05.083. |
| [15] | ZHANG Zhao-shun(张兆顺), CUI Gui-xiang(崔桂香), XU Chun-xiao(许春晓). Theory and modeling of turbulence(湍流理论与模拟)[M].Beijing(北京): Tsinghua University Press(清华大学出版社), 2005. |
| [16] | Zarei S, Ganji H, Sadi M, et al. Thermo-kinetic modeling and optimization of the sulfur recovery unit thermal stage[J]. Applied Thermal Engineering, 2016, 103: 1095-1104. DOI:10.1016/j.applthermaleng.2016.05.012. |
| [17] | Manenti F, Papasidero D, Frassoldati A, et al. Multi-scale modeling of Claus thermal furnace and waste heat boiler using detailed kinetics[J]. Computers & Chemical Engineering, 2013, 59: 219-225. |
| [18] | ZHANG Min-hua(张敏华), BAI Lu(百璐), GENG Zhong-feng(耿中峰), et al. CFD simulation of fluid flow and heat transfer of single phase inside the shell side of multitubular fixed bed reactor(列管式固定床反应器管束间单相流动与传热的CFD研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2013, 27(2): 222-227. |
| [19] | ZHU Bing-chen(朱炳辰). Chemical reaction engineering(化学反应工程)[M].Beijing(北京): Chemical Industry Press(化学工业出版社), 2001. |




