2. 西安交通大学 化学工程与技术学院,陕西 西安 710049
2. School of Chemical Engineering and Technology, Xi'an Jiaotong University, Xi'an 710049, China
大型空分设备的发展,对板翅式换热器的综合性能提出了新的要求。板翅式换热器的综合性能主要包括流动换热性能和承压能力,翅片作为板翅式换热器中最重要的结构,其结构尺寸对板翅式换热器的综合性能影响较大。因此研究翅片结构尺寸如何影响板翅式换热器综合性能就显得十分重要。当前国内外的研究多集中在流动换热性能,ISMAIL等[1]对波纹翅片进行数值模拟,研究了3个无量纲参数对传热和阻力特性的影响,指出翅片表面横向涡是强化传热的关键。MAHDAVI等[2]利用Galerkin方法对波纹翅片流道内二维流动进行分析,发现表面热流率和传热系数之间存在非线性关系。高强等[3]对正弦波纹翅片表冷器的传热及阻力特性进行了实验研究,发现湿工况下传热性能比干工况下高出5%~40%,并拟合得到总传热系数及阻力特性的经验关联式。杨志[4]利用稳态试验法分析了不同流态下翅片的波动幅度对换热器的传热和阻力特性的影响,其结果表明在过渡流状态下波动幅度对波纹翅片的传热和综合性能的影响较大,随着波动幅度的增大,波纹翅片的综合性能下降。
本文以板翅式换热器波纹翅片为研究对象,选取翅高、翅距、翅厚、波长以及双波高作为输入参数来驱动几何模型的生成,并且根据波纹翅片结构特点,提出2个无量纲参数波纹尺度和波纹幅度来替代波长和波高进行研究,结合动态Kriging响应面和遗传算法,以JF因子最大和翅片结构中应力极值τmax最小为优化目标,对波纹翅片结构进行了性能优化研究。
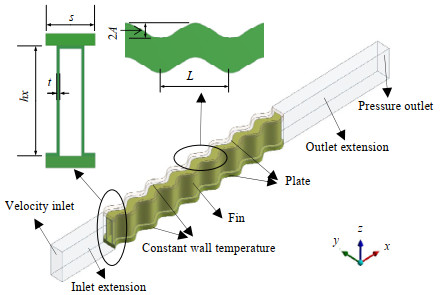
2 几何结构与数值计算模型 2.1 几何模型与计算边界条件图 1为计算几何模型,其中翅片参数包括翅高h、翅距s、翅厚t、波长L以及双波高2A。
|
图 1 几何模型 Fig.1 The geometric model of the design |
由于波纹翅片是通过波纹来加剧流体内部的搅混,因此波长和双波高之间存在较强的耦合作用。为了进一步刻画波长和双波高对翅片性能的影响,本文引入了2个无量纲参数:波纹尺度ws以及波纹幅度wa,其定义如下:
| $ \text{ws}=2A/s $ | (1) |
| $ \text{wa}=2A/L $ | (2) |
在进行模拟计算时,入口边界条件设为速度入口,入口温度为300 K。由于在翅片结构的进出口处添加了延长段,为了维持通道内的雷诺数不变,需要将延长段入口速度进行换算,计算方法如下:
| $ Re=\frac{\rho uD}{\mu } $ | (3) |
| $ {{u}_{\text{in }}}{{A}_{\text{in }}}=u{{A}_{\text{c}}} $ | (4) |
本文中当量直径定义为
| $ D=\frac{4(h-t)(s-t)}{(s+h-2t)} $ | (5) |
出口边界条件设为压力出口,上下隔板表面边界条件设为定壁温(373.15 K);侧面设定为对称边界条件,板翅材料为铝,且忽略与外界的辐射与对流传热,通道流体为空气,且假定其物性为常物性。固体域的约束条件为:在底面限制其沿竖直方向的位移,上表面加载恒定的压力0.606 MPa。通道中设置为恒定压力0.101 MPa,忽略通道内部沿流动方向的压降。
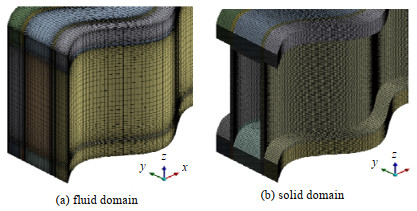
计算模型的网格由mesh模块生成,采用扫掠式网格划分方法得到规整的结构化网格,如图 2所示。由于流体流动边界层和热边界层在靠近壁面的区域,速度梯度和温度梯度较大,为更加精细地刻画该区域内流动换热情况,应对近壁区进行加密处理。
|
图 2 流体与固体域网格划分示意图 Fig.2 Schematic diagram of fluid and solid domain meshing |
在求解过程中,动量方程及能量方程的离散格式采用二阶迎风格式,湍流模型选择标准
求解中涉及的基本方程包括连续性方程、动量方程和能量方程,以及应力计算方程,具体方程可参见文献[5]。
2.3 数据处理[6]由数值模拟得到的数据,可以分别通过计算得到翅片的传热因子j和摩擦因子f。
其中,传热因子j的定义方程为
| $ j=\frac{Nu}{\mathit{Re}P{{r}^{1/3}}} $ | (6) |
摩擦因子f的定义方程为
| $ f=\frac{\Delta pD}{2\rho u_{\text{m}}^{2}l} $ | (7) |
选用JF因子作为翅片的综合性能指标,
| $ JF=j/{{f}^{1/3}} $ | (8) |
翅片的最大应力也是翅片性能优化的目标之一,计算如下,
| $ {{\sigma }_{\text{r4}}}=\sqrt{\frac{1}{2}\left[ {{\left( {{\sigma }_{1}}-{{\sigma }_{2}} \right)}^{2}}+{{\left( {{\sigma }_{2}}-{{\sigma }_{2}} \right)}^{2}}+{{\left( {{\sigma }_{3}}-{{\sigma }_{1}} \right)}^{2}} \right]} $ | (9) |
其中,
为保证计算结果的准确性,同时缩短计算时间,对生成的网格进行了独立性验证,当网格数量约为230万时,j和f因子的计算值基本不发生变化(变化量小于1%),当固体域网格达到约260万时,最大应力的计算值基本不发生变化(变化量小于1%)。
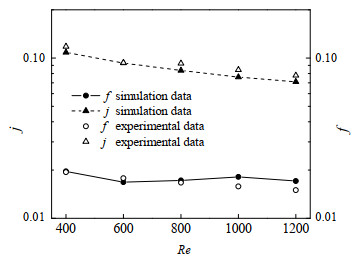
为了验证数值模拟的正确性,将模拟计算值与文献[7]中波纹翅片的实验值进行对比,结果如图 3所示。从图中可以看出,j因子和f因子均和实验数据吻合较好。j因子数值模拟结果与实验值的平均误差为5.5%,而f因子数值模拟结果与实验值的平均误差为7.4%,二者误差均低于10%,说明计算结果在一定程度上可以反映实际情况。对于数值模拟结果和实验结果之间的偏差,其主要原因可能是计算模型的简化,一方面可能没有考虑到翅片表面粗糙度的影响,另一方面可能没有考虑翅片和隔板间钎焊的影响。
|
图 3 实验验证 Fig.3 Experimental verification |
遗传算法的优化过程包括初始实验设计、构造响应面和优化目标函数[6]。实验设计选择中心组合设计法,该方法具有试验次数少、精度高、预测性好的特点。实验设计点的数值模拟结果用来构建响应面,响应面可以近似目标函数与设计变量之间的关系。在响应平面的基础上,采用多目标遗传算法(MOGA)对结构进行优化。这种基于响应面技术的优化研究,是利用响应面创建的输入、输出函数,而非传统的经验关联式,所以在处理无经验关联式或者经验关联式不够准确的情况下非常有效,只要其几何模型能够参数化,优化目标能够量化为目标函数,即可采用多目标遗传算法来进行优化。
3.2 特征数优化范围用波纹尺度ws以及波纹幅度wa来代替波长和双波高这两个参数进行多参数优化研究,依据中心组合设计方法(CCD),针对目前波纹翅片主要使用的翅片参数范围,此次选取的优化范围如下:h为4.5~9.5 mm;s为1.0~3.0 mm;t为0.1~0.3 mm;ws为1.0~3.0;wa为1/6~1/4;Re为400~1 200。
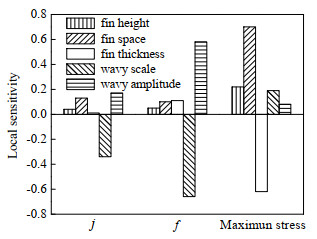
4 结果分析与讨论 4.1 翅片参数对翅片性能的影响 4.1.1 翅片参数的敏感性分析图 4是设计点处局部敏感性分析结果图。对于j因子,影响最大的结构参数为波纹尺度ws以及波纹幅度wa,翅距对j因子也有较大影响,翅高和翅厚对j因子的影响不显著。对于f因子,波纹尺度ws以及波纹幅度wa的影响明显大于翅高、翅厚、翅距3个翅片基本参数,说明波纹翅片主要依靠波纹结构来影响流动换热。对于最大应力,翅厚和翅距对其影响非常显著,其他参数也在较大程度上影响最大应力,所以结构参数的改变会导致最大应力的较大变化,因此在对波纹翅片承压能力要求较高的场合,在设计中需要选择合适的结构参数来避免局部应力过大的情况。
|
图 4 敏感性分析 Fig.4 Sensitivity analysis |
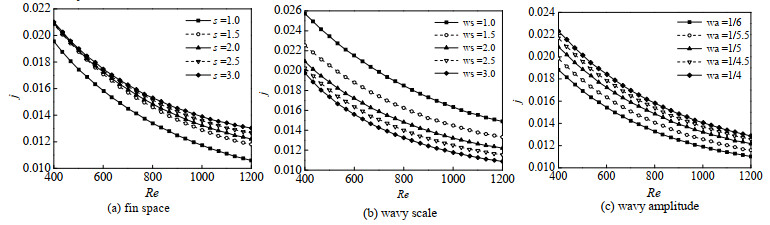
翅距对j因子的影响如图 5(a)所示,增大翅距会使j因子增大。翅距增大,水力直径增加使得一次表面面积增大,传热得到强化,故j因子增大。且随着雷诺数的增大,翅距对j因子的正相关性进一步增大。这是因为尽管水利直径的增加使得流速有所降低,但翅距的增大对波纹翅片流道中二次流的形成起到了强化的作用,流体内掺混加剧,而当雷诺数越大时,流体内部黏滞阻力对二次流的抑制作用越弱,二次流更易形成。由于流体内部流态与搅混对传热的强化作用要大于流速的作用,故当雷诺数较高时,增大翅距会使j因子进一步增大。
|
图 5 翅片参数对j因子的影响 Fig.5 Effects of fin geometric parameters on factor j |
波纹尺度ws对j因子的影响如图 5(b)所示,波纹尺度增大,j因子减小,并且波纹尺度越小时,这种减小幅度越明显。当波纹尺度较小时,波纹结构明显,对流体的搅混作用强烈,而随着波纹尺度的增加,流道结构由波纹型几何特征变为类似弯管流道的几何特征,波纹结构对流体的搅混作用不再明显。波纹幅度wa对j因子的影响如图 5(c)所示,增大波纹幅度会使得j因子增大。波纹幅度越大,波纹结构的几何特征越明显,其对流体的搅混作用越强烈,j因子增大。从图中可以观察到,随着波纹幅度的增加,j因子的提升速率越来越慢,提升空间越来越小。这是由于当波纹幅度增大到一定程度后,在波谷处会形成漩涡与流动死区,导致波纹结构对主流区的搅混不充分,传热性能提升不大。
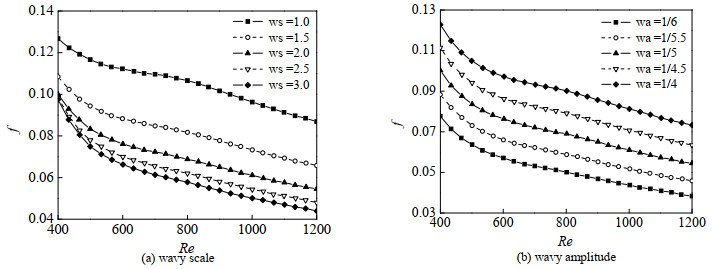
4.1.3 翅片参数对f因子的影响波纹尺度ws对f因子的影响如图 6(a)所示,波纹尺度增大,f因子减小,并且波纹尺度越小时,这种减小幅度越明显。这与波纹尺度对j因子的影响机理相同,在波纹翅片的结构设计中,应当特别关注波纹尺度,过大的波纹尺度会抑制二次流的形成,削弱强化传热效果,而太小的波纹尺度又会导致压降的激增。
|
图 6 翅片参数对f因子的影响 Fig.6 Effects of fin geometric parameters on factor f |
波纹幅度wa对f因子的影响如图 6(b)所示。增大波纹幅度会使f因子增大。波纹幅度越大,波纹结构的几何特征越明显,其对流体的搅混作用越强烈,f因子增大。值得注意的是,随着波纹幅度的增加,f因子的增加程度远大于j因子的提升程度。在设计波纹翅片时应当注意到,虽然波纹幅度的增加会使得j因子有明显的上升,但是j因子有提升的极限,并且与此同时f因子会迅速提高,因此波纹幅度不应过大,在各结构参数无限制的情况下应优先通过波纹尺度来提升传热性能。
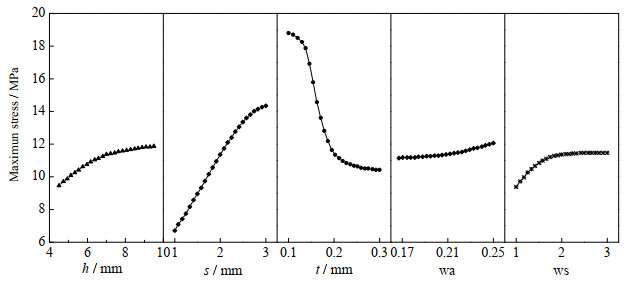
4.1.4 翅片参数对承压能力的影响各结构参数对翅片承压能力的影响,如图 7所示。随着翅高增加,波纹翅片的最大应力逐渐升高,最大增幅25.7%。这是由于当翅高增加时,翅片横截面的支撑部分由“短粗形”向“细长形”转变,导致应力增大。所以随着翅高的增加,换热器的承压能力逐渐降低。在对换热器承压能力要求较高的场合,不宜选用翅高过大的翅片结构。
|
图 7 翅片参数对承压能力的影响 Fig.7 Effects of fin geometric parameters on maximum stress |
随着翅距的增加,波纹翅片的最大应力显著升高,最大增幅为116.2%。这是由于当翅距增加时,隔板受压的面积增大,故总压力升高,但与此同时翅厚保持不变,即承压部分的面积不变,故承压面积与受压面积之比减小,即单位面积下承压结构需要承受更大的压力,导致最大应力增大。所以随着翅距的增加,换热器的承压能力逐渐降低。
随着翅厚的增加,波纹翅片的最大应力显著降低,最大降幅为43.0%,与翅距的影响效果相反,当翅厚增加时,承压面积相对受压面积有所增加,故单位面积下承压结构需要承受的压力减小,导致其最大应力减小。所以随着翅厚的增加,换热器承压能力显著提高。
随着波纹尺度和波纹幅度的增大,最大应力均有所升高,当波纹尺度增大时,最大应力增幅为22.5%,当波纹幅度增大时,最大应力增幅为8%,说明波纹结构对承压能力的影响有限。
4.2 优化结果本文选取JF因子最大和翅片结构中应力极值τmax最小为优化目标,在Re=800的工况条件下对翅片各参数进行结构优化,得到26组可行解,其中3组典型结构优化结果在表 1中列出,同时给出一组工业上常用的波纹翅片结构[8]作为对比。由于优化结果是基于Kriging响应面所得到的近似值,为验证结果的准确性,将优化结果的性能预测值与CFD计算值进行对比。从表 1中可以看出,各预测值与计算值之间的偏差均小于10%,说明结合动态Kriging响应面与遗传算法可以有效对板翅式换热器翅片结构进行优化设计。根据表中优化结果可知,相较于常用结构,优化后翅片热性能因子可提升5.8%~7.8%,而最大应力可降低7.3%~22.8%。
|
|
表 1 波纹翅片优化结果 Table 1 Optimization results of wavy fins |
针对板翅式换热器波纹翅片进行参数化建模,采用基于响应面分析的多目标遗传算法,从流动、换热和应力3个方面对翅片结构进行了分析及多目标优化,结论如下:
(1) 波纹翅片参数的敏感性分析研究表明,波纹尺度ws、波纹幅度wa和翅距s对j因子的影响较大,波纹尺度ws和波纹幅度wa对f因子的影响较大,翅厚和翅距对最大应力影响非常显著,其他参数也在较大程度上影响最大应力,结构参数的改变会导致最大应力的较大变化。
(2) 翅片参数对翅片性能的影响表明,波纹翅片结构参数主要通过改变换热面积,改变流速以及加剧流体内部搅混来改变流动换热特性,其中加剧流体内部搅混为主要影响途径,且横向二次流影响效果明显大于纵向二次流影响效果。换热面积的改变与流速的改变效果相近,影响相反,对于不同结构参数体现出不同的综合影响效果。
(3) 以JF因子最大和翅片结构中应力极值τmax最小为优化目标,得到了3组最优结构参数组合,相较于常用结构,优化后翅片热性能因子可提升5.8%~7.8%,而最大应力可降低7.3%~22.8%。
符号说明
|
|
| [1] |
ISMAIL L S, VELRAJ R. Studies on Fanning friction (f) and Colburn (j) factors of offset and wavy fins compact plate fin heat exchanger-a CFD approach[J]. Numerical Heat Transfer, Part A:Applications, 2009, 56(12): 987-1005. DOI:10.1080/10407780903507957 |
| [2] |
MAHDAVI A, DELAVAR M A. Thermal performance of wavy fin in a compact heat exchanger duct using Galerkin method[J]. Applied Thermal Engineering, 2018, 130(1): 1290-1298. |
| [3] |
高强, 王秋旺, 王家贵. 正弦波纹翅片表冷器的传热及阻力特性实验研究[J]. 制冷学报, 2007, 28(5): 1-5. GAO Q, WANG Q W, WANG J G. Study on heat transfer and friction characteristics of sinusoidal wavy type cooling coil[J]. Journal of Refrigeration, 2007, 28(5): 1-5. DOI:10.3969/j.issn.0253-4339.2007.05.001 |
| [4] |
杨志.空分用板翅式换热器波纹翅片传热与阻力性能理论与实验研究.[D].杭州: 浙江工业大学, 2013. YANG Z. Theoretical and experimental research on the heat transfer and pressure drop characteristics of wavy fin of plate fin heat exchanger in air separation plant[D]. Hangzhou: Zhejiang University Of Technology, 2013. |
| [5] |
文键, 李科, 刘育策, 等. 利用流固耦合分析的板翅式换热器锯齿型翅片多目标优化[J]. 西安交通大学学报, 2018, 52(02): 130-135. WEN J, LI K, LIU Y C, et al. Multi-objective optimization of serrated fin in plate-fin heat exchanger by fluid structure interaction[J]. Journal of Xi'an Jiaotong University, 2018, 52(2): 130-135. |
| [6] |
杨辉著, 文键, 童欣, 等. 板翅式换热器锯齿型翅片参数的遗传算法优化研究[J]. 西安交通大学学报, 2015, 49(12): 90-96. YANG H Z, WEN J, TONG X, et al. Optimization design for offset fin in plate heat exchanger with genetic algorithm[J]. Journal of Xi'an Jiaotong University, 2015, 49(12): 90-96. |
| [7] |
KAYS W M, LONDON A L. Compact heat exchanger[M]. New York: McGraw-Hill, 1964: 97-112.
|
| [8] |
王松汉. 板翅式换热器[M]. 北京: 化学工业出版社, 1984. WANG S H. Plate-fin heat exchanger[M]. Beijing: Chemical Industry Press, 1984. |




