换热网络综合已成为化工系统研究的难点,国内外相关研究从优化方法的角度主要分为夹点分析和数学规划法[1]。夹点分析[2]最早由LINNHOFF等提出,以热力学为基础,分析过程系统中的温度分布,选择合适的夹点温度及组合匹配方式以实现能量的最大回收利用。
数学规划法可分为确定性方法和启发式算法[3-5]。确定性方法如牛顿法[6-8]、最速下降法[9]、分支定界法[10]等,这些方法在求解具有非凸特性的混合整数非线性规划问题时,求解效率较低,不能满足大规模系统计算需求。而启发式算法如模拟退火算法(simulated annealing, SA)[11-12]、禁忌算法(Tabu search, TS) [13]、微分进化算法(differential evolution, DE) [14]、遗传算法(genetic algorithm, GA) [15]及粒子群算法(particle swarm optimization, PSO) [16]等,能够利用已有的经验规则,随机搜索求解域内的全局最优解。启发式算法可操作性强,计算效率高,因此在换热网络最优化问题中得到越来越多的应用。但是在种群进化后期,由于种群多样性的缺失,启发式算法容易出现早熟收敛的问题。同时大规模系统的求解难度和复杂程度不断增加,影响优化效率和优化精度。
为了提高启发式算法应用于大规模系统的优化质量,提升算法的全局优化性能。肖媛等[17]总结了启发式算法应用于换热网络优化的特点,揭示了其早熟收敛现象的本质,并在此基础上提出了一种新的强制进化随机游走算法(random walk algorithm with compulsive evolution, RWCE)。相比于其他启发式算法,RWCE具有程序简单、算法适应性强的特点,具备跳出局部最优解的能力,从而提升了换热网络的优化质量。
采用RWCE优化换热网络,分析其优化进程。发现个体在每次进化时都是以一定的几率随机参与游走,因此在优化过程中不一定每股流体上都有换热单元被选中参与进化。对于没有参与进化的流股,该次迭代便没有意义。如要保证每股流体都进化一次需要增加大量的迭代次数,使得换热网络的进化效率低下。故本文提出以热流体为基准每股流体必进化策略,即每隔一定周期强制使得每股流体上都有换热单元被选中参与进化,并每隔一定步数强制接受每股流体都游走的结构,使其跳出局部极值,提升算法的优化效率和优化质量。
2 换热网络优化模型换热网络优化问题描述为:以年度总费用(total annual cost,TAC)最低为目标,通过在NH股热流体与NC股冷流体之间设置换热单元及冷、热公用工程,使冷热流体达到目标温度,实现能量回收。本文采用换热网络节点非结构模型[18],以2股热流体和2股冷流体为例,非结构模型如图 1所示。其中,H1、H2表示两股热流体,C1、C2表示两股冷流体,公用工程布置在冷热流股末端,每股冷热流体上分别预设NGDC、NGDH个产生换热单元的位置。
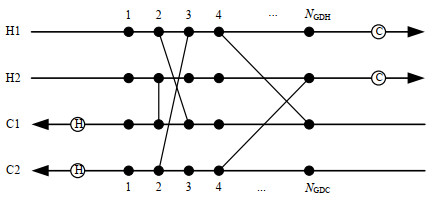
|
图 1 非结构模型结构图 Fig.1 Non-structural model structure |
本文基于换热网络非结构模型,以TAC最小为目标,数学描述为:
该模型包含NH股热流体、NC股冷流体,热流体上共有NKH个节点,冷流体上共有NKC个节点,NKH = NH × NGDH,NKC = NC × NGDC。TAC如式(1)和(2)所示。
| $ \min \text{TAC}=\min \sum\limits_{n=1}^{{{{{N}'}}_{\text{h, c}}}}{({{F}_{\text{G0}}}+{{C}_{\text{A0}}}A_{EX}^{\text{ }\beta \text{ }})+\sum\limits_{i=1}^{{{N}_{\text{H}}}}{({{F}_{\text{G}1}}+{{C}_{\text{A}1}}A_{\text{CU}, i}^{\text{ }\beta \text{ }}}+{{C}_{\text{CU}}}{{Q}_{\text{CU}, i}})\\+\sum\limits_{j=1}^{{{N}_{\text{C}}}}{({{F}_{\text{G}2}}+{{C}_{\text{A}2}}A_{\text{HU}, j}^{\text{ }\beta \text{ }}+{{C}_{\text{HU}}}{{Q}_{\text{HU}, j}})}} $ | (1) |
| $ {{{N}'}_{\rm{h, c}}}=\sum\limits_{n=1}^{{{N}_{\text{KH}}}}{\sum\limits_{i=1}^{{{N}_{\text{KC}}}}{C'{{N}_{\rm{h, c}}}}} $ | (2) |
式中,TAC表示年度综合费用;FG表示固定投资费用;CA表示换热单元的面积费用系数;A表示设备面积,m2;β表示面积费用指数;Q表示公用工程热负荷,kW;C表示公用工程费用系数;下角标CU表示冷公用工程,HU表示热公用工程;z, i, j分别表示换热单元数、热流体数和冷流体数,z∈Nh, c,i∈NH,j∈NC;Nh, c表示可能存在的所有换热单元的个数,N'h, c实际存在的换热单元的个数,C’表示换热单元是否存在的0-1变量。
换热单元的热负荷及面积的热平衡关系式如式(3)和(4)所示。
| $ {{Q}_{\text{h, c}}}=(T_{\text{h}}^{\text{in}}-T_{\text{h}}^{\text{out}})\times {{F}_{\text{cp}, i}}=(T_{\text{c}}^{\text{out}}-T_{\text{c}}^{\text{in}})\times {{F}_{\text{Cp}, j}} $ | (3) |
| $ {{A}_{\text{h, c}}}={{Q}_{\text{h, c}}}/\left( {{K}_{i, j}}\times \text{LMT}{{\text{D}}_{\text{h, c}}} \right) $ | (4) |
式中,h表示热流体上的节点,c表示冷流体上的节点;T表示温度,℃;in表示进口,out表示出口;Fcp, i为第i股热流体的热容流率,Fcp, j为第j股冷流体的热容流率,kW·℃-1;Ki, j为第i股热流体与第j股冷流体上的节点匹配产生的换热单元的传热系数,kW·(m2·℃)-1;LMTDh, c为冷热流体上进出口温度的对数平均温差,计算公式如式(5)所示。
| $ {\rm{LMTD}}{_{\text{h, c}}}=\left[ \left( T_{\text{h}}^{\text{in}}-T_{\text{c}}^{\text{out}} \right)-\left( T_{\text{h}}^{\text{out}}-T_{\text{c}}^{\text{in}} \right) \right]/\text{ln}\left[ \left( T_{\text{h}}^{\text{in}}-T_{\text{c}}^{\text{out}} \right)/\left( T_{\text{h}}^{\text{out}}-T_{\text{c}}^{\text{in}} \right) \right] $ | (5) |
特别地,当Thin - Tcout = Thout - Tcin时,可采用算数平均温差代替对数平均温差,计算公式如式(6):
| $ \text{LMT}{{\text{D}}_{\text{h, c}}}=\left[ \left( T_{\text{h}}^{\text{in}}-T_{\text{c}}^{\text{out}} \right)+\left( T_{\text{h}}^{\text{out}}-T_{\text{c}}^{\text{in}} \right) \right]/2 $ | (6) |
RWCE的基本思想[17]是:随机产生初始换热网络结构,以目标函数TAC减小为强制进化方向,随机改变换热单元的面积实现连续变量和整型变量的同步优化;当游走到局部最优点时,以一定几率随机接受差解,使其跳出局部极值,寻找全局最优。主要操作步骤为:
(1) 种群初始化。随机产生初始种群M,其中包含n个个体Zi,i = 1, …, n,每个个体对应一个换热网络结构。初始种群表示如式(7)~(9)所示。
| $ M={{Z}_{i}}\times {{Q}_{\text{h, c}}}=0 $ | (7) |
| $ {{H}_{\text{M}}}=0 $ | (8) |
| $ {{C}_{\text{M}}}=0 $ | (9) |
其中,Qh, c表示热流体上的h节点与冷流体上的c节点处匹配产生的换热单元的热负荷,h = 1, …, NH·NGDH, c = 1, …, NC·NGDC;HM表示换热单元在热流体上的节点编号,CM表示换热单元在冷流体上的节点编号。
(2) 进化阶段。
a.存在的个体进化。判断热负荷大于0的个体,即判断已存在换热单元的个体,对种群内部已存在的个体以一定概率进行随机游走操作,主要方式如式(10)~(13)所示。
| $ {{\left( {{Q}_{\text{h, c}}} \right)}_{it}}={{\left( {{Q}_{\text{h, c}}}' \right)}_{it-1}} $ | (10) |
| $ {{\left( Q{{'}_{\text{h, c}}} \right)}_{it}}={{\left( {{Q}_{\text{h, c}}} \right)}_{it}}+\Delta {{Q}_{\text{h, c}}} $ | (11) |
| $ \Delta {{Q}_{\text{h, c}}}={{Q}_{\text{max}}}\times \left( 1-2{{\alpha }_{\text{h, c}}} \right)\Delta L{{\beta }_{\text{h, c}}} $ | (12) |
| $ {{\left( {{Q}_{\text{h, c}}} \right)}_{it+1}}={{\left( Q{{'}_{\text{h, c}}} \right)}_{it}} $ | (13) |
其中,it为迭代次数,Qh, c为个体当前次迭代的初始热负荷,ΔQh, c为游走的热负荷大小,
进化过程中,最小热负荷被作为该换热单元是否存在的临界尺度,如式(14)所示。
| $ Q{{'}_{\text{h, c}}}=\left\{ \begin{align} & Q{{'}_{\text{h, c}}}\;\;\;\text{if}Q{{'}_{\text{h, c}}}>\Delta L\eta \\ & 0\;\;\;\;\;\text{else} \\ \end{align} \right. $ | (14) |
其中,η为保留系数,指可保留的最小热负荷与最大游走步长ΔL的比值。
b.新个体产生阶段。随机选择冷热流股上的节点,判断该节点处是否存在换热单元,若不存在,则在该位置以一定概率随机生成一定热负荷的换热单元。如式(15)~(17)所示。
| $ u={{N}_{\text{KH}}}\times {{\gamma }_{1}};v={{N}_{\text{KC}}}\times {{\gamma }_{2}} $ | (15) |
| $ Q=\Delta {{Q}_{\text{max2}}}\times \gamma $ | (16) |
| $ \left\{ \begin{align} & {{Q}_{\text{u, v}}}=Q\;\;\;\;\;\;\text{if} ({{Q}_{\text{u, c}}}=0, \text{and}, {{Q}_{\text{h, v}}}=0) \\ & u={{N}_{\text{KH}}}\times {{\gamma }_{1}};v={{N}_{\text{KC}}}\times {{\gamma }_{2}}\;\;\;\;\;\;\text{else} \\ \end{align} \right. $ | (17) |
其中,γ,γ1,γ2为0到1之间均匀分布的随机数;u为热流体上节点,v为冷流体上节点,Qp, q为在u,v节点处新生成换热单元的热负荷。
(3) 个体选择阶段。迭代后,若TAC比前一次迭代值更低,则接受该次迭代的换热网络结构,并将该结构对应的热负荷及节点编号作为下一次迭代的初始结构;若迭代后,TAC不低于上一次迭代的值,则以一定概率δ接受该次迭代的换热网络结构作为下一次迭代的初始结构;否则不更新该个体。如式(18)所示。
| $ {\left( {{Q_{{\rm{h, c}}}}} \right)_{it + 1}} = \left\{ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\left( {Q{'_{{\rm{h, c}}}}} \right)_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}} {\kern 1pt} \left( {{{\left( {{\rm{TAC}}'} \right)}_{it}} < {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left( {{\rm{TAC}}} \right)}_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} } \right)\\ {\kern 1pt} {\left( {Q{'_{{\rm{h, c}}}}} \right)_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}}\left( {r < \delta } \right)\\ {\kern 1pt} {\left( {{Q_{{\rm{h, c}}}}} \right)_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{else}} \end{array} \right. $ | (18) |
其中,r为0到1之间均匀分布的随机数。
(4) 终止条件。记录迭代过程中TAC最低的换热网络结构,当满足终止条件时,迭代终止。
3.2 以热流体为基准每股流体必游走策略相较于其他优化方法,RWCE优化换热网络能得到较低的TAC,但是需要较长的计算时间,优化效率仍有待提高。研究发现个体在每次进化时都以一定几率随机选择已存在的换热单元参与进化,且进化几率值较低,因此不能确定每次进化时每股流体上都有换热单元被选中参与进化。以13股热流体7股冷流体的算例为例,进化过程中的节点选中几率设为0.2,分析每次进化时流体不被选中的几率。
由图 2可知,进化前期,换热单元数目存在较大波动时,流股被选中几率也有较大变化;进化后期,换热单元数基本固定在某一数值附近,此时每股流体不被选中的几率基本固定在0.74左右。即在进化后期,13股热流体中平均每次迭代只能选中3股左右参与进化。对于当前次进化没有被选中的流股,该次迭代就没有意义;要保证每股流体都进化一次需要消耗大量的迭代次数,对换热网络的进化产生不利影响。针对此特点,采取以热流体为基准每股流体必游走策略,即采取措施使得每隔一定周期每股流体上都至少有一个换热单元被选中参与进化,从而均匀地增加每股流体的进化几率,以提升换热网络的优化效率。
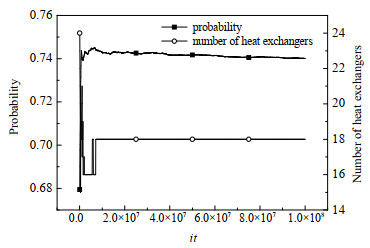
|
图 2 流股未被选中几率 Fig.2 The probability of the stream unselected in each iteration |
主要策略是在存在的个体进化处采取措施。在个体进化之前,预先判断每股流体上已经存在的换热单元数,重新编号,并与原来的编号一一对应。每隔itG1次迭代,采取一次每股流体上都有一个换热单元被选中参与进化的措施;其余迭代步数以原有的进化方式随机参与进化。其中,itG1表示采取必游走策略的迭代周期。每隔一定周期采取一次每股流体必游走策略,既能在个体进化到一定程度之后给种群一定的方向指导,又能在其他迭代期间使种群保持原有的随机进化方向,保留其随机性特点。
以13股热流体7股冷流体的算例[19] (算例1)为例,流股参数如表 1所示。采用RWCE优化换热网络并采取每股流体必游走策略,当参数设为:NGDH = 10,NGDC = 10,ΔL = 100,η = 0.2,δ = 0.01,Qmax = 100,itG1 = 1 000时,TAC变化曲线如图 3示。
|
|
表 1 算例1参数数据 Table 1 Flow parameters of case 1 |
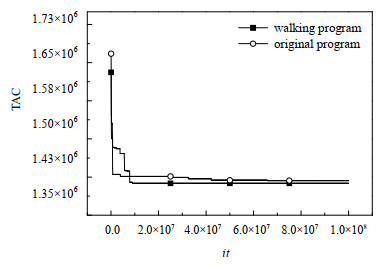
|
图 3 必游走TAC变化曲线图 Fig.3 TAC curve for the participatory evolution strategy for streams |
由图 3可知,采取必游走策略的RWCE能比原始RWCE以更快的速度寻找到具有更低TAC的结构,有效提高了算法的优化质量。
3.3 以热流体为基准每股流体必进化策略采用加入每股流体必游走策略的RWCE优化换热网络,分析发现,只在存在的个体进化处采取措施,不能保证每次进化之后的个体一定会被接受。采取必游走策略之后,每股流体上都有换热单元的热负荷发生变化,故该次迭代后的费用很大几率上比前一次迭代的费用高。此时,进化后较高费用的结构便不会被接受。因此该策略只能在一定程度上改变进化方向,不能从根本上跳出局部极值。为充分发挥必游走策略的方向指导作用,进一步在个体选择位置采取措施,每隔itG2次迭代强制接受一次每股流体必游走之后的结构,即每股流体必进化策略,其中itG2表示强制接受每股流体必游走之后的结构的迭代周期。
每隔一定周期采取一次每股流体必进化策略,使得换热网络的优化既能够保留原有进化方法的随机性特性,又能给该随机进化方法一定的方向指导,更快速地找到更优的结构。以13股热流体7股冷流体和8股热流体7股冷流体的算例[26] (算例2)为例,采用RWCE优化换热网络并采取每股流体必进化策略,8股热流体7股冷流体的算例流股参数如表 2所示。当将13股热流体7股冷流体的算例参数设为:NGDH = 10,NGDC = 10,ΔL=100,η = 0.2,δ = 0.01,Qmax = 100,itG1 = 1 000,itG2 = 5.5×106时,采取必进化策略的TAC与原程序的TAC变化曲线如图 4、图 5示。
|
|
表 2 算例 2 参数数据 Table 2 Flow parameters of case 2 |

|
图 4 必进化实时TAC变化曲线图 Fig.4 TAC curve for compulsive participatory evolutionary strategy in the real time |
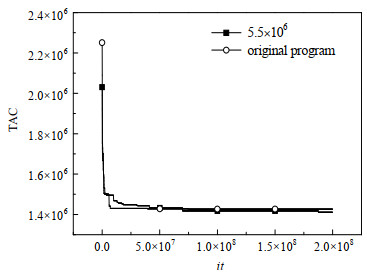
|
图 5 必进化最优TAC变化曲线图 Fig.5 Lowest TAC curve for compulsive participatory evolutionary strategy |
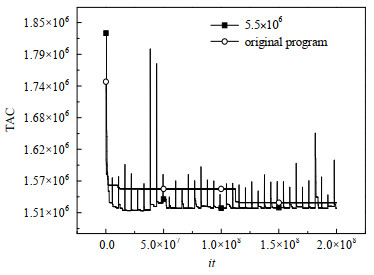
当将8股热流体7股冷流体的算例参数设为:NGDH = 10,NGDC = 10,ΔL = 110,η = 0.2,δ = 0.01,Qmax = 100,ITG1 = 1 000,ITG2 = 5.5×106时,采取必进化策略的TAC与原程序的TAC变化曲线如图 6、图 7所示。
|
图 6 必进化实时TAC变化曲线图 Fig.6 TAC curve for the compulsive participatory evolutionary strategy in the real time |

|
图 7 必进化最优TAC变化曲线图 Fig.7 Lowest TAC curve for compulsive participatory evolutionary strategy |
由图可知,采取每股流体必进化策略的RWCE,能以更高的速率找到更优解,显著地提高了RWCE的求解速率及求解质量。在每股流体必进化策略中,每一次强制接受每股流体必游走的结构之后,费用会急剧增加,但每次的费用增加,都会打破原有的进化方向,跳出局部极值,从而增强RWCE的局部搜索能力。
3.4 改进RWCE步骤将结合上述策略的改进RWCE应用于换热网络优化,存在的个体进化部分的改进步骤如下:
Step 1:判断已经存在换热单元的位置,将已存在的换热单元重新编号,并与原来的节点编号一一对应;
Step 2:对种群内部的所有个体进行随机游走操作:每隔一定迭代次数采取一次每股流体上至少有一个换热单元被选中参与游走的措施,其余迭代步数仍按照原来的进化几率进行随机游走操作;
个体选择部分的改进步骤为:
Step 1:每隔一定迭代次数后强制接受一次当前迭代后的结构:经过it次迭代,无论TAC是否比上一次迭代更低,都强制接受该换热网络结构及每个节点的热负荷,并将该结构的热负荷作为第(it+1)次迭代的初始热负荷。如式(19)所示。
| $ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left( {{Q_{{\rm{h, c}}}}} \right)_{it + 1}} = {\left( {Q{'_{{\rm{h, c}}}}} \right)_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} $ | (19) |
Step 2:其余迭代次数仍以得到更低的TAC为目标,进行随机游走操作。经过it次迭代,若TAC比上一次迭代更低,则接受换热网络结构及每个节点的热负荷,并将该结构的热负荷作为第(it+1)次迭代的初始热负荷,否则不更新该个体,保持第it次迭代的换热网络结构及热负荷。如式(20)所示。
| $ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left( {{Q_{{\rm{h, c}}}}} \right)_{it + 1}} = \left\{ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\left( {Q{'_{{\rm{h, c}}}}} \right)_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}} {\kern 1pt} \left( {{{\left( {{\rm{TAC}}'} \right)}_{it}} < {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left( {{\rm{TAC}}} \right)}_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} } \right)\\ {\kern 1pt} {\left( {{Q_{{\rm{h, c}}}}} \right)_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{else}} \end{array} \right. $ | (20) |
Step 3:变异操作。若经过it次迭代,TAC不低于上一次迭代的费用,则以一定概率δ接受该次迭代的换热网络结构及热负荷,作为第(it+1)次迭代的初始结构及初始热负荷。如式(21)所示。
| $ {\left( {{Q_{{\rm{h, c}}}}} \right)_{it + 1}} = \left\{ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\left( {Q{'_{{\rm{h, c}}}}} \right)_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}} {\kern 1pt} \left( {{{\left( {{\rm{TAC'}}} \right)}_{it}} < {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left( {{\rm{TAC}}} \right)}_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} } \right)\\ {\kern 1pt} {\kern 1pt} {\left( {Q{'_{{\rm{h, c}}}}} \right)_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}} (r < \delta ){\kern 1pt} {\kern 1pt} {\kern 1pt} \\ {\kern 1pt} {\kern 1pt} {\left( {{Q_{{\rm{h, c}}}}} \right)_{it}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{else}} \end{array} \right. $ | (21) |
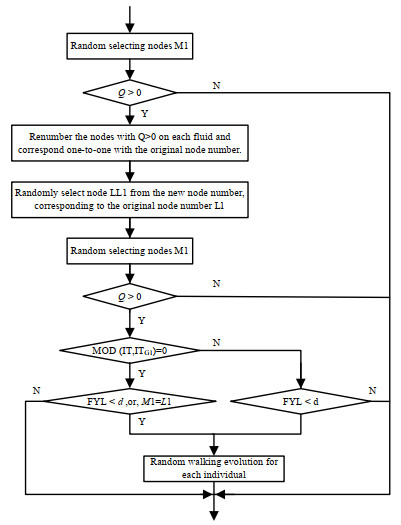
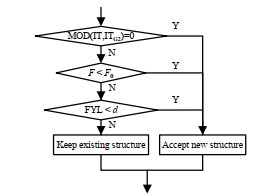
其中,r为0到1之间均匀分布的随机数,δ为当(it+1)次迭代的TAC大于it次迭代时,更新换热网络结构,接受差解的概率。其算法流程图如图 8,9,10所示。
|
图 8 存在的个体进化 Fig.8 Random walk evolution for each individual in the population |
|
图 9 个体选择阶段 Fig.9 Individual selections |

|
图 10 必进化策略流程图 Fig.10 Flow chart of the weighted evolutionary strategy |
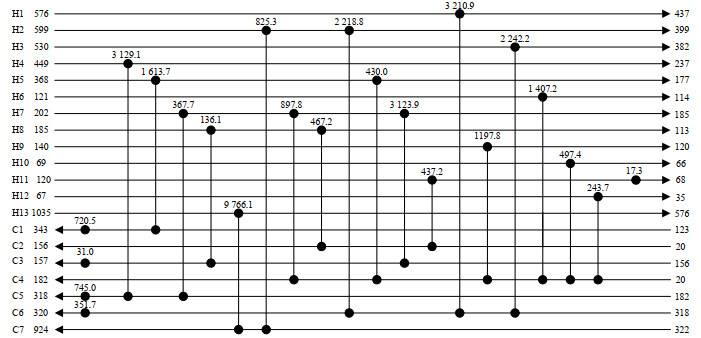
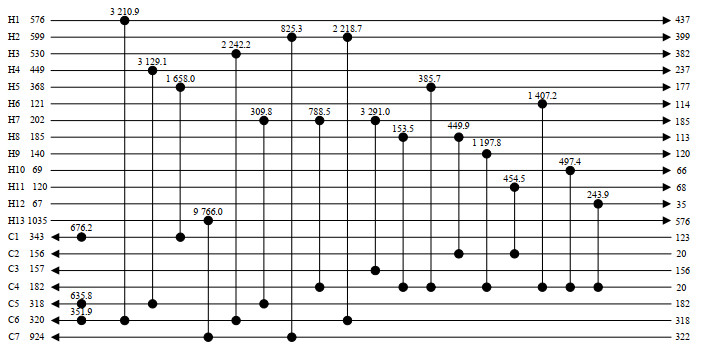
文献中的优化方法大多基于YEE等[20-22]提出的分级超结构模型进行的。ESCOBAR等[23]采用等温混合假设法,得到算例1的TAC为1 537 086 $·a-1。Pavão等[24]采用改进的粒子群算法,得到TAC为1 516 482 $·a-1;BAO等[25]采用保护最优解策略的RWCE,得到TAC为1 462 363 $·a-1。本文采用每股流体必游走策略的RWCE,得到的TAC为1 432 904 $·a-1,费用结构图如图 11所示;采用每股流体必进化策略的RWCE,得到的TAC为1 411 131 $·a-1,费用结构图如图 12所示;算例1的结果对比如表 3所示。
|
图 11 采用每股流体必游走策略的RWCE优化结果 Fig.11 RWCE optimization results using the participatory evolutionary strategy for streams |
|
图 12 采用每股流体必进化策略的RWCE优化结果 Fig.12 RWCE optimization results using the compulsive participatory evolutionary strategy |
|
|
表 3 算例1优化结果对比 Table 3 Comparison on optimized results of case 1 |
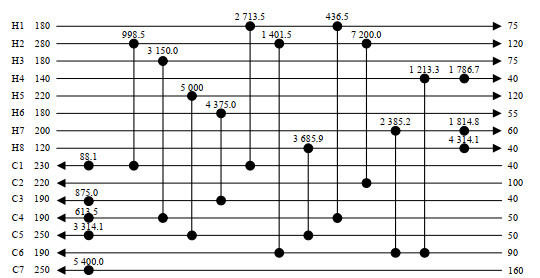
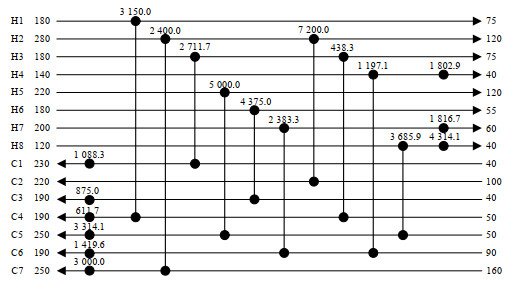
BJORK等[26]采用数学规划法改造换热网络得到算例2的TAC为1 530 063 $·a-1;PENG等[27]采用改进模拟退火算法得到的TAC为1 527 240 $·a-1;LEANDRO等[28]采用模拟退火算法和粒子群算法相结合的双层优化方法,得到的TAC为1 525 394 $·a-1;本文采用每股流体必游走策略的RWCE,得到的TAC为1 519 791 $·a-1,费用结构图如图 13所示;采用每股流体必进化策略的RWCE,得到的TAC为1 518 969 $·a-1,费用结构图如图 14所示;算例2的结果对比如表 4所示。
|
图 13 采用每股流体必游走策略的RWCE优化结果 Fig.13 RWCE optimization results using the participatory evolutionary strategy for streams |
|
图 14 采用每股流体必进化策略的RWCE优化结果 Fig.14 RWCE optimization results using the compulsive participatory evolutionary strategy |
|
|
表 4 算例2优化结果对比 Table 4 Comparison on optimized results of case 2 |
由算例1及算例2的优化结果及对比可知,在相同的目标函数、约束条件和费用系数等条件下,RWCE算法能比其他优化方法以更快的速度得到更优的结果,尤其是改进的RWCE算法。采用以热流体为基准每股流体必进化策略的RWCE算法,有效提高了换热网络的优化效率及优化质量。
5 结论本文提出的以热流体为基准每股流体必进化策略的RWCE算法,能够在保留非结构模型一定自由性的基础上,给非结构模型一定的方向指导。既不破坏非结构模型的自由性与灵活性,也能够使非结构模型的优化目标更趋向于全局最优解,从而提高换热网络的优化质量。
通过两个不同规模的算例验证提出的策略,得到的结果分别为1 411 131和1 518 969 $·a-1。结果表明,采用每股流体必进化策略的换热网络优化方法能够有效提高非结构模型的优化质量。
但是每股流体必进化策略仍存在一定的不足。在换热网络优化后期,出现不存在公用工程的流股,此时采用每股流体必进化策略的效果便不如预期。因此每股流体必进化策略的优化方法仍需继续深入研究,以改进该策略在换热网络优化后期的不足,进一步提升该策略在换热网络非结构模型中的优化质量。
| [1] |
LINNHOFF B, DUNFORD H, SMITH R. Heat integration of distillation columns into overall processes[J]. Chemical Engineering Science, 1983, 38(8): 1175-1188. DOI:10.1016/0009-2509(83)80039-6 |
| [2] |
LINNHOFF B, HINDMARSH E. The pinch design method for heat exchanger networks[J]. Chemical Engineering Science, 1983, 38(5): 745-763. DOI:10.1016/0009-2509(83)80185-7 |
| [3] |
PREMKUMAR R, RANGAIAH G P. Retrofitting conventional column systems to dividing-wall columns[J]. Chemical Engineering Research & Design, 2009, 87(1): 47-60. |
| [4] |
张慧平.过程系统工程综合方法及其求解策略的研究[D].北京: 北京化工大学, 2000. ZHANG H P. Research on process systems engineering synthesis method and solution strategy[D]. Beijing: Beijing University of Chemical Technology, 2000. |
| [5] |
MORAR M, AGACHI P S. Review:Important contributions in development and improvement of the heat integration techniques[J]. Computers & Chemical Engineering, 2010, 34(8): 1171-1179. |
| [6] |
COLEMAN T F, CONN A R. On the local convergence of a quasi-Newton method for the nonlinear programming problem[J]. IAM Journal on Numerical Analysis, 1982, 21(4): 755-769. |
| [7] |
SALIM M S, AHMED A I. A family of quasi-Newton methods for unconstrained optimization problems[J]. Optimization, 2018, 1-11. |
| [8] |
WANG X, MA S, GOLDFARB D, et al. Stochastic quasi-Newton methods for nonconvex stochastic optimization[J]. Siam Journal on Optimization, 2017, 27(2): 927-956. |
| [9] |
TSENG P, YUN S. A coordinate gradient descent method for nonsmooth separable minimization[J]. Mathematical Programming, 2009, 117(1/2): 387-423. |
| [10] |
QUESADA I, GROSSMANN I E. Global optimization algorithm for heat exchanger networks[J]. Industrial & Engineering Chemistry Research, 1993, 32(3): 487-499. |
| [11] |
DOLAN W B, CUMMINGS P T, VAN L. Algorithmic efficiency of simulated annealing for heat exchanger network design[J]. Computers & Chemical Engineering, 1990, 14(10): 1039-1050. |
| [12] |
PENG F Y, CUI G M. Efficient simultaneous synthesis for heat exchanger network with simulated annealing algorithm[J]. Applied Thermal Engineering, 2015, 78: 136-149. DOI:10.1016/j.applthermaleng.2014.12.031 |
| [13] |
DIPAMA J, TEYSSEDOU A, SORIN M. Synthesis of heat exchanger networks using genetic algorithms[J]. Applied Thermal Engineering, 2008, 28(14/15): 1763-1773. |
| [14] |
方大俊, 崔国民. 微分进化算法应用于换热网络全局最优化[J]. 化工学报, 2013, 64(9): 3285-3290. FANG D J, CUI G M. Global optimization of heat exchanger networks using differential evolution algorithm[J]. CIESC Journal, 2013, 64(9): 3285-3290. |
| [15] |
LIN B, MILLER D C. Solving heat exchanger network synthesis problems with Tabu search[J]. Computers & Chemical Engineering, 2004, 28(8): 1451-1464. |
| [16] |
SILVA A P, RAVAGNANI M S, JR E B. Particle swarm optimization applied in retrofit of heat exchanger networks[J]. Computer Aided Chemical Engineering, 2009, 27(9): 1035-1040. |
| [17] |
肖媛, 崔国民, 李帅龙. 一种新的用于换热网络全局优化的强制进化随机游走算法[J]. 化工学报, 2016, 67(12): 5140-5147. XIAO Y, CUI G M, LI S L. A novel random walk algorithm with compulsive evolution for global optimization of heat exchanger networks[J]. CIESC Journal, 2016, 67(12): 5140-5147. |
| [18] |
肖媛.换热网络热集成的全局优化方法及超结构模型研究[D].上海: 上海理工大学, 2018. XIAO Y. Global optimization methods and superstructure for heat integration of heat exchanger networks[D]. Shanghai: University of Shanghai for Science And Technology, 2018. |
| [19] |
SILVA A P, RAVAGNANI M S, BISCAIA E C. Particle swarm optimization applied in retrofit of heat exchanger networks[J]. Computer Aided Chemical Engineering, 2009, 27(9): 1035-1040. |
| [20] |
YEE T F, Grossman I E, Kravanja Z. Simultaneous optimization model for heat integration-Ⅰ. Area and energy targeting and modeling of multi-stream exchangers[J]. Computers & and Chemical Engineering, 1990, 14(10): 1151-1164. |
| [21] |
YEE T F, Grossman I E, Kravanja Z. Simultaneous optimization model for heat integration-Ⅱ. Heat exchanger network synthesis[J]. Computers & and Chemical Engineering, 1990, 14(10): 1165-1184. |
| [22] |
YEE T F, Grossman I E, Kravanja Z. Simultaneous optimization model for heat integration-Ⅲ. Process and heat exchanger network synthesis[J]. Computers & and Chemical Engineering, 1990, 14(11): 1185-1200. |
| [23] |
ESCOBAR M, TRIERWEILER J O. Optimal heat exchanger network synthesis:A case study comparison[J]. Applied Thermal Engineering, 2013, 51(1/2): 801-826. |
| [24] |
PAVÃO L V, COSTA C B B. Automated heat exchanger network synthesis by using hybrid natural algorithms and parallel processing[J]. Computers & Chemical Engineering, 2016, 94: 370-386. |
| [25] |
BAO Z K, CUI G M, CHEN J X, et al. A novel random walk algorithm with compulsive evolution combined with an optimum-protection strategy for heat exchanger network synthesis[J]. Energy, 2018, 152: 694-708. DOI:10.1016/j.energy.2018.03.170 |
| [26] |
BJORK K M, NORDMAN R. Solving large-scale retrofit heat exchanger network synthesis problems with mathematical optimization methods[J]. Chemical Engineering and Processing, 2005, 44(8): 869-876. DOI:10.1016/j.cep.2004.09.005 |
| [27] |
PENG F Y, CUI G M. Efficient simultaneous synthesis for heat exchanger network with simulated annealing algorithm[J]. Applied Thermal Engineering, 2015, 78: 136-149. DOI:10.1016/j.applthermaleng.2014.12.031 |
| [28] |
LEANDRO V P, CALIANE B B C. Heat exchanger network synthesis without stream splits using parallelized and simplified simulated annealing and particle swarm optimization[J]. Chemical Engineering Science, 2017, 158: 96-107. DOI:10.1016/j.ces.2016.09.030 |




