有机羧酸如甲酸、乙酸、丙酸、丁酸会同时出现在制药、造纸、石化等工业废水和发酵液中[1, 2]。除上述领域外,劣质煤在低温干馏或气化过程中会产生高浓煤化工含酚废水,不仅含有大量单元酚、多元酚,也含有较高浓度的有机羧酸[3, 4]。高浓煤化工含酚废水在使用溶剂萃取高浓含酚废水中总酚的同时,有机酸也一并萃取出来。这些羧酸是一类非常有价值的精细化学品,其中许多用作食品添加剂和防腐剂,也用于制药和化工行业[1, 2]。去除并回收有价值的羧酸产品既有环境意义又有经济价值。
许多分离方法已被用于脱除这类有机羧酸,如吸附、膜分离、沉淀和液液萃取等[5]。液液相平衡数据的测定不仅可用来测试和改进热力学模型[5],而且对精确模拟和设计液液萃取过程单元极其重要。流程模拟软件对未有精确二元交互作用参数输入的体系进行计算时,准确度大大降低,而二元交互作用参数往往是通过实验测定的液液相平衡数据拟合回归得到。甲基叔丁基醚作为可替代四乙基铅的优良防爆剂和汽油添加剂,推动着其大规模生产的发展,其合成工艺简单,原料易得,成本相对较低,因此本文选择沸点较低、成本较低和同时对单元酚和多元酚都有较好萃取性能的甲基叔丁基醚作为萃取剂[6]。在完成甲基叔丁基醚-苯酚[7]/甲酚[8~10]/苯二酚[11]/丙酸/丁酸[12]-水液液相平衡测定后,进一步开展了甲基叔丁基醚-丙酸-丁酸-水四元体系液液相平衡实验研究,该体系先前未有报道。
文献[7~14]在高浓煤化工含酚废水液液萃取相平衡方面进行了大量研究和探索,为相关三元和四元体系测定和模型参数回归提供研究基础。废水处理领域液液相平衡四元体系研究中,又大致分两类研究体系:两种萃取剂、水和被萃取物[15~17];两种被萃取物、水和萃取剂[11, 13]。本文的体系属于后者,测定了甲基叔丁基甲醚-丙酸-丁酸-水液液相平衡数据,利用Bachman方程、Othmer-Tobias方程和Hand方程对液液相平衡数据的热力学一致性进行研究,用NRTL方程和UNIQUAC方程对实验数据进行回归拟合,得到二元交互作用参数,为准确模拟利用甲基叔丁基醚萃取含丙酸/丁酸废水的过程设计提供关键数据。
2 实验部分 2.1 试剂和仪器试剂:试剂均为分析纯,实验中无需进一步纯化。甲基叔丁基甲醚,国药集团化学试剂有限公司;丙酸、丁酸和异丁酸,成都西亚试剂;甲醇,上海凌峰化学试剂有限公司;正丁醇,江苏强盛功能化学股份有限公司。蒸馏水,超纯水设备制备。这些试剂纯度均采用Agilent气相色谱GC6820测试验证。它们的密度、折射率与文献值进行了对比,列于表 1中。
| 表 1 本文涉及化学试剂的纯度、密度和折射率 Table 1 Purity, density (ρ) and refractive index (nD) of chemicals used in this work at 298.15K and 101.325 kPaa |
仪器:液液相平衡釜 (自制),HWS-24型电热恒温水浴锅 (上海一恒科技有限公司),DJ-1型磁力搅拌器 (江苏金坛亿通电子有限公司),Agilent GC6820气相色谱仪。
2.2 实验装置及方法相平衡实验时,预先配制含有三种物质的酸水溶液,将其与一定量的MTBE混合即可,其中酸水溶液中,丙酸和丁酸分别按照质量组成[m×丙酸+(1-m)×丁酸]比例混合。根据称量结果,m分别取0.2571、0.5178、0.7406,丙酸和丁酸总质量约为30 g。接着分别配制60 mL不同m值的酸水溶液于3个如图 1所示的150 mL自制的平衡釜中,再加入适量的甲基叔丁基甲醚 (MTBE) 构成四元体系,加入磁石后用磁力搅拌器激烈搅拌至少2 h。搅拌完毕后,将平衡釜置于精度为±0.1℃的恒温水浴锅中,在298.15 K下静置18 h以上,此后有机相和水相出现明显分层达到相平衡,用注射器分别抽取有机相和水相进行测定,取样以及测定方法同三元液液萃取相平衡实验。每次取样后,都向平衡釜加入5 mL甲基叔丁基甲醚重复上述步骤,进行下一组实验数据的测定。图 2是MTBE-m×丙酸-(1-m)×丁酸-水的四元体系示意相图。
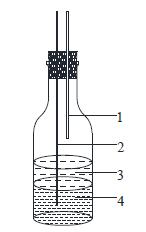
|
图 1 平衡釜 Fig.1 Schematic diagram of the equilibrium vessel used in the study 1. organic sample outlet 2. aqueous sample outlet 3. organic phase 4. aqueous phase |
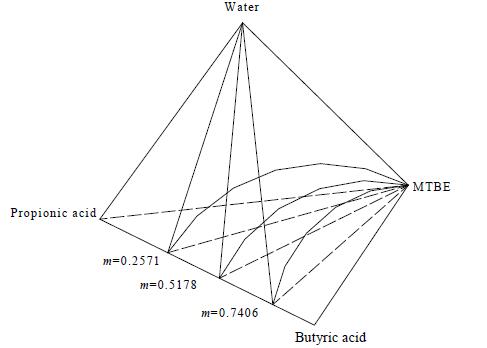
|
图 2 MTBE-m×丙酸-(1-m)×丁酸-水四元体系示意相图 Fig.2 Scheme of phase diagram for the quaternary system MTBE +m ×propionic acid+ (1-m) × butyric acid + water (m is the mass ratio of propionic acid to propionic acid + butyric acid) at 298.15 K |
样品的分析测定采用安捷伦气相色谱仪,其中色谱柱选用Agilent DB-FFAP 30 m×0.32 mm×0.5 μm。采用0.5 μL (有机相) 或1 μL (水相) 的微量进样器手动进样,检测器为氢火焰离子化检测器 (FID)。
选用甲醇作为MTBE的内标物,异丁酸同时作为丙酸、正丁酸的内标物。在进行定量分析之前需要测定各组分及其对应的内标物之间的内标系数,也称作内标因子fi:
| ${f_i} = \frac{{{A_t} \cdot {m_i}}}{{{A_i} \cdot {m_t}}}$ | (1) |
式中Ai,At分别是组分i的峰面积和组分i对应的内标物的峰面积;mi,mt分别是组分i的质量和组分i对应的内标物的质量。在测量内标系数的实验中,每个样品的测量次数至少为3次,最终测得MTBE、丙酸、正丁酸对应的内标系数分别为0.5305、1.3168、1.0552。
得到各组物质内标系数后就可以计算出液液萃取相平衡中各组分 (除水之外) 的浓度 (质量分数):
| ${w_i} = \frac{{{m_i}}}{{{m_S}}} = \frac{{{f_i} \cdot {A_i} \cdot {m_t}}}{{{A_t} \cdot {m_S}}}$ | (2) |
式中mi,ms,mt分别表示样品中组分i的质量、样品的质量以及组分i对应的内标物的质量;Ai,At分别是组分i的峰面积和组分i对应的内标物的峰面积。样品中的水由于氢火焰离子化检测器无法对其响应,故在气相色谱谱图中无法显示。由于样品中除水之外的所有物质都能够出峰,且都能得到准确的质量浓度,因此,样品中水的含量可通过下面公式 (归一法) 获得:
| ${w_{{H_2}O}} = 1 - \sum {{w_i}} $ | (3) |
液液相平衡实验测定过程中的误差有内标系数测定的误差、恒温水浴锅控温误差 (±0.1℃)、分析天平误差 (0.1 mg) 和微量进样器进样时样品里面组分的挥发误差。其中0.1℃的温度微小变化对液液相平衡的移动来说影响很小;分析天平的误差通过控制取样质量在50 mg以上,以使质量误差在0.2%以下;微量进样器吸取样品的近距离快捷操作使得误差控制在极小的范围内。
因此,最大的误差来源是内标系数测定误差。测定某一内标系数时,通过配制至少50个样品,每个样品至少测定3次的方式使得内标系数误差控制在2%以下。
3 实验结果与讨论 3.1 液液相平衡数据的测定MTBE-丙酸-丁酸-水四元体系在温度为298.15 K下的液液相平衡数据列于表 2中。其中w1、w2、w3、w4分别代表MTBE,丙酸、丁酸和水在各自相溶液中的浓度,D2、D3分别代表丙酸和丁酸的分配系数。
| 表 2 MTBE (1) +丙酸 (2) +丁酸 (3) +水 (4) 四元体系液液相平衡数据 Table 2 Experimental LLE data (mass fraction) of the quaternary system MTBE (1) + propionic acid (2) +butyric acid (3) + water (4) at T=298.15 K and p=101.3 kPa |
根据表 2的数据,分别作出在不同m值下的丙酸和丁酸在MTBE-丙酸-丁酸-水四元体系的平衡分配曲线,如图 3所示。由图 3(a)可知,四元体系中随着丙酸比例的增加,萃取相和萃余相中丙酸的浓度都相应增加;萃余相同一浓度下,随着丙酸比例的增加,萃取相中丙酸的浓度增大,相应丙酸的分配系数也增加;同一丙酸、丁酸比例下,随着萃余相浓度增加,萃取相中丙酸的浓度也增加。图 3(b)中丁酸也呈现类似的规律现象。综合图 3(a)和图 3(b)可知,丙酸比例的增加意味着体系中丁酸比例的减少,并且同一体系中丙酸的分配系数始终比丁酸的低。
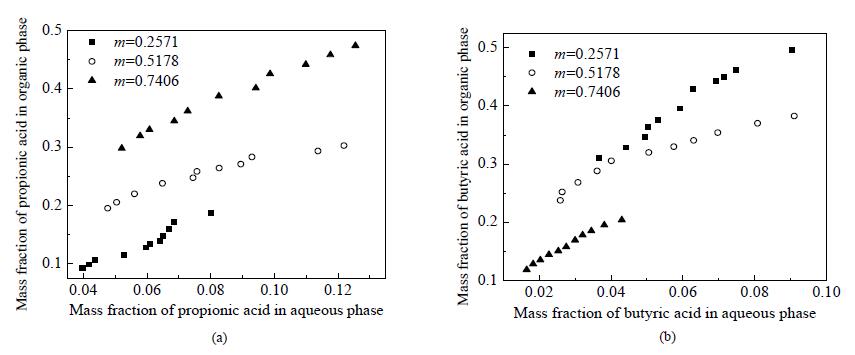
|
图 3 25℃时不同质量比m下丙酸 (a) 和丁酸 (b) 在MTBE有机相和水相中的平衡分布线 Fig.3 Equilibrium distribution lines of propionic acid (a) and butyric acid (b) between organic and aqueous phases of the quaternary system under different m values at T=298.15 K |
为了检验四元实验数据的热力学一致性,分别采用Bachman方程[18]、Hand方程[19]和Othmer-Tobias方程[20]对298.15 K下的MTBE-丙酸-丁酸-水四元体系液液萃取相平衡数据进行关联。三个方程的表达式分别为:
| $\ln \left( {\frac{{w_{2 + 3}^O}}{{w_1^O}}} \right) = {a_1} + {b_1}\ln \left( {\frac{{w_{2 + 3}^W}}{{w_4^W}}} \right)$ | (4) |
| $w_1^O = {a_2} + {b_2}\left( {\frac{{w_1^O}}{{w_4^W}}} \right)$ | (5) |
| $\ln \left( {\frac{{1 - w_1^O}}{{w_1^O}}} \right) = {a_3} + {b_3}\ln \left( {\frac{{1 - w_4^W}}{{w_4^W}}} \right)$ | (6) |
式中,
将表 2的数据分别代入公式 (4)~(6),回归出的各个方程的参数 (a和b) 见表 3,其线性关系见图 4(a)、(b)和(c),表 3中各个方程的拟合度R2大都接近0.99,说明四元实验数据可靠,均具有较好的一致性。
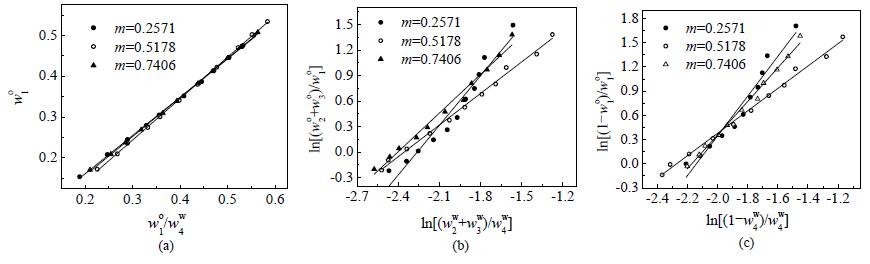
|
图 4 MTBE (1) +丙酸 (2)+丁酸 (3) +水 (4) 四元体系的Bachman方程 (a)、Hand方程 (b) 和Othmer-Tobias方程 (c) 线性图 Fig.4 Bachman, Hand and Othmer-Tobias plots of the quaternary system MTBE (1) +propionic acid (2) + butyric acid (3) + water (4) |
| 表 3 Bachman、Hand和Othmer-Tobias方程参数 Table 3 Fitting parameters of Bachman, Hand and Othmer-Tobias equations |
验证完萃取液液相平衡实验数据的可靠性后,用活度系数模型中的NRTL模型方程和UNIQUAC模型方程对表 2中测得的四元相平衡数据进行拟合。拟合结果由ASPEN软件回归得到,本实验回归得到MTBE (1) +丙酸 (2) +丁酸 (3) +水 (4) 四元体系的UNIQUAC和NRTL模型12个二元相互作用参数见表 4。表 4中模型的二元交互作用参数指的是两种物质之间的参数,其中i和j分别代表两种不同的物质,i和j可为1、2、3、4,分别代表MTBE、丙酸、丁酸和水。通过表 4活度系数模型NRTL方程和UNIQUAC方程回归所得的二元交互作用参数,就可对上述四元体系的液液萃取相平衡数据进行预测。
| 表 4 NRTL和UNIQUAC模型二元交互作用参数 Table 4 Binary interaction parameters of NRTL and UNIQUAC models a |
上述四元体系的液液萃取相平衡在25℃下对应的NRTL模型和UNIQUAC模型的数据与实验数据的均方根偏差RMSD的值也同样列于表 4中。均方根偏差RMSD的计算公式为:
| $RMSD(\% ) = 100 \times {\left[ {\frac{{\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^2 {\sum\limits_{k = 1}^n {{{\left( {w_{ijk}^{\exp } - w_{ijk}^{cal}} \right)}^2}} } } }}{{6n}}} \right]^{1/2}}$ | (7) |
式中,m表示总的组分数;n表示总的实验次数 (结线数);
实验测得的液液相平衡数据分别用NRTL模型和UNIQUAC模型对实验数据进行了关联,回归得到了四元体系的活度系数模型二元交互作用参数。二元交互作用参数与对应的活度系数模型相结合,就可以对相应的四元体系的液液萃取相平衡数据进行预测。同时,利用上述两种活度系数模型计算出来的数据与实验数据的均方根偏差均小于0.02,说明两个模型回归得到的二元交互作用参数均能对实验数据进行较精确的预测。甲基叔丁基甲醚对丙酸和丁酸均表现出良好的萃取效果。
| [1] | Ricke S C. Perspectives on the use of organic acids and short chain fatty acids as antimicrobials[J]. Poultry Science , 2003, 82(4): 632-639. DOI:10.1093/ps/82.4.632. |
| [2] | Oliveria M B, Pratas M J, Marrucho I M, et al. Description of the mutual solubilities of fattty acids and water with the CPA Eos[J]. AIChE Journal , 2009, 55(6): 1604-1613. DOI:10.1002/aic.v55:6. |
| [3] | Ji Q H, Tabassum S, Hena S, et al. A review on the coal gasification wastewater treatment technologies:past, present and future outlook[J]. Journal of Cleaner Production , 2016, 126(7): 38-55. |
| [4] | Singer P C, Pfaender F K, Chinchilli J, et al. Assessment of coal conversion wastewater:characterization and preliminary biotreatability[R]. Washington, DC:U.S. EPA, 1978. |
| [5] | Gündogdu T, Çehreli S. Ternary liquid-liquid phase equilibria of (water-carboxylic acid-1-undecanol) systems at 298.15 K[J]. Fluid Phase Equilibria , 2012, 331(1): 26-32. |
| [6] | LEI Yong(雷勇). Study on Liquid-liquid equilibria and process simulation of the extraction system to remove phenols from coal-gasification with MTBE [D]. Guangzhou (广州): South China University of Technology (华南理工大学), 2014. |
| [7] | Lei Y, Chen Y, Li X X, et al. Liquid-liquid equilibria for the ternary system 2-methoxy-2-methylpropane+phenol+water[J]. Journal of Chemical and Engineering Data , 2013, 58(6): 1874-1878. DOI:10.1021/je400295z. |
| [8] | Luo L J, Liu D, Li L B, et al. Measurements and thermodynamic modeling of liquid-liquid equilibria in ternary system 2-methoxy-2-methylpropane+p-cresol+water[J]. Chinese Journal of Chemical Engineering , 2016, 24(3): 360-364. DOI:10.1016/j.cjche.2015.10.011. |
| [9] | Luo L J, Liu D, Li L B, et al. Experimental determination and correlation of liquid-liquid equilibria for the ternary system 2-methoxy-2-methylpropane+o-cresol+water at 298.15 K and 313.15 K[J]. Journal of Chemical and Engineering Data , 2015, 60(5): 1396-1400. DOI:10.1021/je501114q. |
| [10] | Luo L J, Li L B, Liu D, et al. Ternary liquid-liquid equilibria for the system 2-methoxy-2-methylpropane+m-cresol+water at 298.15 and 313.15 K:experimental data and correlation[J]. Journal of Solution Chemistry , 2015, 44(12): 2393-2404. DOI:10.1007/s10953-015-0418-x. |
| [11] | Chen Y, Lei Y, Li X X, et al. Measurements of liquid-liquid equilibria for the quaternary system 2-methoxy-2-methylpropane+phenol+hydroquinone+water at 313.15 K[J]. Journal of Chemical and Engineering Data , 2013, 58(10): 2793-2798. DOI:10.1021/je400488x. |
| [12] | Luo L J, Liu D, Li L B, et al. Phase equilibria of (water+propionic acid or butyric acid+2-methoxy-2-methylpropane) ternary systems at 298.2K and 323.2K[J]. Fluid Phase Equilibria , 2015, 403(10): 30-35. |
| [13] | Wang H M, Wang Z, Li L B, et al. Ternary and quaternary liquid-liquid equilibria for systems of methyl butyl ketone+water+hydroquinone+phenol at 313.2 K and atmospheric pressure[J]. Journal of Chemical and Engineering Data , 2016, 61(4): 1540-1546. DOI:10.1021/acs.jced.5b00918. |
| [14] | Liu D, Li L B, Luo L J, et al. Liquid phase equilibria of the water+propionic or butyric acid+methyl tert-butyl ketone ternary systems at 298.15 and 323.15K[J]. Journal of Chemical and Engineering Data , 2015, 60(9): 2612-2617. DOI:10.1021/acs.jced.5b00214. |
| [15] | ZHANG Yu-chi(张于弛), QIU Ting(邱挺). Determination and correlation of liquid-liquid equilibrium data for the methyl acetate-methanol-water-acetic acid quaternary system[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2013, 27(3): 380-385. |
| [16] | Toikka M, Samarov A, Toikka A. Solubility, liquid-liquid equilibrium and critical states for the system acetic acid+n-propanol+n-propyl acetate+water at 293.15K and 303.15[J]. Fluid Phase Equilibria , 2014, 375(8): 66-72. |
| [17] | Samarov A, Toikka M, Toikka A. Liquid-liquid equilibrium and critical states for the system acetic acid+n-butanol+n-butyl acetate+water at 308.15 K[J]. Fluid Phase Equilibria , 2015, 385(1): 129-133. |
| [18] | Bachman I. Tie lines in ternary liquid systems[J]. Industrial & Engineering Chemistry Analytical Edition , 1940, 12(1): 38-39. |
| [19] | Hand D B. Dineric distribution[J]. The Journal of Physical Chemistry , 1930, 34(9): 1961-2000. |
| [20] | Othmer D, Tobias P. Liquid-liquid extraction data-the line correlation[J]. Industrial & Engineering Chemistry , 1942, 34(6): 693-696. |




