2. 陕西省洁净煤转化工程技术中心,陕西 西安 710069
2. Shaanxi Research Center of Engineering Technology for Clean Coal Conversion, Xi'an 710069, China
喷动床技术在煤气化、热解、烟气脱硫及催化聚合等工业过程中存在着广泛应用[1~7]。传统柱锥型喷动床内介质颗粒具有明显的内外分层流动特点,床层内颗粒缺少横向混合,特别是在环隙区底部出现流动死区和某些易粘结颗粒的团聚现象,对床内传热传质产生不利的影响。为克服以上不利现象,新一代喷动-流化床兼有喷动床与流化床的优点而得到了喷动床研究者与流化床研究者的共同重视及发展[6, 7],但也存在不足,如维持这种喷动-流化床所需的气体流量比单独喷动和单独流化所需的气流量要大,同时增加了一定的旁路供气辅助设备[6]。针对以上柱锥喷动床技术现状,本文提出了一种新型整体式多喷嘴喷动-流化床结构[8](图 1所示),在不需要旁路供气辅助设备情况下,能有效消除喷动床内锥体流动死区,强化喷动床内气固相间传递过程,从而使喷动床内气固两相流动状态实现整体优化。
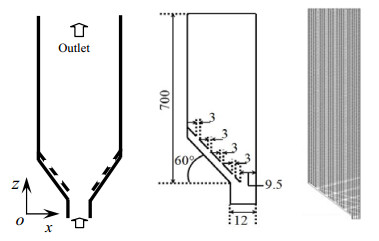
|
图 1 多喷嘴喷动–流化床结构示意图及网格划分(单位:mm) Fig.1 Geometry and grids of a multi-jet spout-fluidized bed (unit: mm) |
随着计算机技术和计算流体力学的飞速发展,数值模拟被广泛用于流态化过程研究[9~17]。由于实验中装置、仪器及经费等的限制问题,且实验研究中存在难以测量的一些过程和细节,而计算机模拟可以作为与理论分析和实验研究互补的一种重要方法, 对深化了解喷动床内气固两相流动规律起到了重要的作用。Wang等[9]采用双流体模型来研究油页岩喷动床气固两相流的流动形式,模拟得到了稳定的喷动三区。Liu等[10]采用三维欧拉-欧拉多相模型来模拟预测喷动床最小喷动速度,通过不断降低入口气速观察颗粒体积分数分布、颗粒速度来确定最小喷动速度。Lan等[11]研究了喷动床固相壁面边界条件、弹性系数以及颗粒与壁面恢复系数的影响。模拟结果表明,固相壁面边界条件对喷动床模拟影响很大,恢复系数、壁面剪切应力对颗粒体积分数分布和喷动高度有很大影响。Yang等[12]则采用CFD-DEM方法对一个三维的平行双槽矩形喷动床内颗粒流体运动规律进行了模拟分析,从微观的角度对喷动床的启动过程及其典型的流动结构进行了模拟分析,研究了床层的流体力学分布特性,并讨论了湍流模型对气固两相流动的影响规律。Hosseini等[14]采用双流体模型对矩形喷动床内气固两相流动进行了流体动力学分析,几何模型采用了二维和三维方法,研究发现三维模型对发射系数和粒子-壁面碰撞恢复系数敏感度较二维模型高。Qiu等[15]通过CFD-DEM方法数值模拟研究了喷动床的宽度参数对三维及准三维喷动床内的气固两相流动规律的影响,研究表明:随着喷动床宽度参数的增加,最小喷动速度和最大压降呈现出先减小后保持不变的规律。文献[16]采用双流体模型数值模拟分析了不同的径向分布函数表达式对喷动床内气固两相流动特性的影响规律,并与实验数据进行了相关的对比分析。任立波等[17]发展了基于FLUENT软件信息传递模式的MPICH2并行计算平台及一种非结构网格下拟三维颗粒的CFD-DEM耦合并行算法。本文基于He[18, 19]的实验数据及文献[20]的数值模拟模型,采用Fluent15.0软件对整体式多喷嘴喷动-流化床内两相流动进行了数值模拟,并将模拟结果与常规喷动床结果进行了比较分析,特别是环隙区底部(圆锥处)的气固两相流动特性,并对关键设计参数(锥面侧喷嘴参数)进行了优化,从而为整体式多喷嘴喷动-流化床的工程设计提供理论依据。
2 数学模型 2.1 质量守恒方程| $ 连续方程\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\partial }{\partial t}\left( {{\varepsilon }_{\text{i}}}{{\rho }_{\text{i}}} \right)+\nabla \cdot \left( {{\varepsilon }_{\text{i}}}{{\rho }_{\text{i}}}{{\nu }_{\text{i}}} \right)=0 $ | (1) |
其中,i表示气体或颗粒相,ε为气体或颗粒浓度,v为气体或颗粒速度矢量,ρ是气体或颗粒的密度。
2.2 动量守恒方程气体动量守恒方程[6]可表示为:
| $ \frac{\partial }{\partial t}\left( {{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}{{\nu }_{\text{g}}} \right)+\nabla \cdot \left( {{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}{{\nu }_{\text{g}}}{{\nu }_{\text{g}}} \right)=-{{\varepsilon }_{\text{g}}}\nabla {{P}_{\text{g}}}+{{\varepsilon }_{\text{g}}}{{\rho }_{\text{g}}}g+{{\beta }_{\text{gs}}}\left( {{\nu }_{\text{s}}}-{{\nu }_{\text{g}}} \right)+\nabla \cdot {{\tau }_{\text{g}}} $ | (2) |
其中,g是重力加速度,Pg是气体压力,βg是气体-颗粒相间的曳力系数,τg是气体应力张量。
颗粒相动量守恒方程:
| $ \frac{\partial }{\partial t}\left( {{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}{{\nu }_{\text{s}}} \right)+\nabla \cdot \left( {{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}{{\nu }_{\text{s}}}{{\nu }_{\text{s}}} \right)=-{{\varepsilon }_{\text{s}}}\nabla {{P}_{\text{g}}}+\nabla \cdot {{\tau }_{\text{s}}}+{{\varepsilon }_{\text{s}}}{{\rho }_{\text{s}}}g+{{\beta }_{\text{gs}}}\left( {{\nu }_{\text{g}}}-{{\nu }_{\text{s}}} \right) $ | (3) |
其中,τs是固相应力张量。
2.3 曳力模型Gidaspow曳力模型[7]相间动量交换系数Kgs的计算方法如下:
当α ≤ 0.8,气固相间动量交换系数Kgs为
| $ {{K}_{\text{Ergun}}}=150\frac{\alpha _{_{\text{s}}}^{\text{2}}{{\mu }_{\text{g}}}}{{{\alpha }_{\text{g}}}{{d}^{2}}}+1.75\frac{{{\rho }_{\text{g}}}{{\alpha }_{\text{s}}}}{d}\left| {{\overrightarrow{v}}_{\text{g}}}-{{\overrightarrow{v}}_{\text{s}}} \right| $ | (4) |
当α > 0.8,气固相间动量交换系数Kgs为
| $ {{K}_{\text{Wen-Yu}}}=\frac{3{{C}_{\text{D}}}{{\alpha }_{\text{g}}}{{\alpha }_{\text{s}}}{{\rho }_{\text{g}}}\left| {{\overrightarrow{v}}_{\text{g}}}-{{\overrightarrow{v}}_{\text{s}}} \right|}{4{{d}_{\text{p}}}}\varepsilon _{\text{g}}^{\text{-2}\text{.65}} $ | (5) |
| $ 其中,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{C}_{\text{D}}}=\frac{24}{{{\alpha }_{\text{g}}}R{{e}_{\text{s}}}}\left( 1+0.15R{{e}^{0.687}} \right),Re\le 1000 $ | (6) |
| $ {{C}_{\text{D}}}=0.44,\ R{{e}_{\text{S}}}\ge 1000 $ | (7) |
为了避免Ergun方程与Wen & Yu方程过渡的不连续性,Gidaspow引进了一个选择函数使两个方程平滑而快速过渡。
| $ {{\varphi }_{\text{gs}}}=\frac{\text{arctan}\left[ 150\times 1.75\left( 0.2-{{\alpha }_{\text{s}}} \right) \right]}{\pi }+0.5 $ | (8) |
则气固相间动量交换系数Kgs为
| $ {{K}_{\text{gs}}}={{\varphi }_{\text{gs}}}{{K}_{\text{Wen-Yu}}}+\left( 1-{{\varphi }_{\text{gs}}} \right){{K}_{\text{Ergun}}} $ | (9) |
喷动床进口气体采用速度进口边界条件,出口为流体充分发展边界条件,壁面采用无滑移边界条件。模型引入Gidapows曳力模型和颗粒动力学理论分别描述气固相间作用力和颗粒相应力。采用SIMPLE算法求解离散方程组的压力和速度耦合,迭代时间步长为2×10-5s,计算残差小于10-3。
3 模拟结果与分析本文数值模拟喷动床的几何尺寸,气相和颗粒相的物理特性都与文献[18, 19]中的常规喷动床相同,由于物理问题的对称性,取多喷嘴喷动-流化床区域的一半作为研究对象进行数值建模。多喷嘴喷动-流化床整体设计尺寸及网格划分情况如图 1所示,模拟设置参数如表 1所示,喷动床圆锥处侧喷嘴标准数量取值为4,侧喷嘴宽度为3 mm。文献[20]在基于He[18, 19]的实验数据上,数值模拟分析了湍流模型对喷动床内气固两相流动的影响,其颗粒速度与实验值的最大模拟偏差为26%,孔隙率的最大模拟偏差为6.9%,表明数值模型具有一定的合理性。由于目前缺乏本文所设计的多喷嘴喷动-流化床内气固两相流动实验数据,本文将采用文献[20]数值模型对多喷嘴喷动-流化床内气固两相流动规律进行模拟分析,并将模拟结果与相应尺寸文献[20]常规喷动床模拟结果进行对比。对模型进行网格无关性分析,计算网格数分别设定为11260、13260、14760及21760。计算表明,数值模拟的精度随网格数的增加而提升,当网格数量大于13260时,数值模拟达到了网格无关性的要求。数值模拟中常规喷动床及多喷嘴喷动-流化床的计算网格数分别为14391和14760。
| 表 1 两种喷动床数值模拟参数值设定 Table 1 Experimental and simulation data for two spouted beds |
图 2为总入口气体速度U = 1.3Ums时,多喷嘴喷动-流化床内颗粒体积分数云图随时间的变化规律。由于流体流动的连续性,中心喷嘴气体流量分布可用中心喷嘴直径与总入口直径之比表示,其余为侧边喷嘴气体流量分布,气体流量分配与中心喷嘴直径及总入口直径比之相关。由图 2可知,在喷动形成前,床体上部颗粒出现腾涌现象,当计算时间大于t = 5 s时,喷动床内气固两相流体流动结构达到稳定。图 3为稳定喷动条件下,多喷嘴喷动-流化床与常规喷动床颗粒体积分数云图的对比情况。由图 3对比情况可以看出,多喷嘴喷动-流化床的侧喷嘴对锥体部固体颗粒层实现了有效扰动,出现多处局部沟流,颗粒体积分数显著下降,增强了环隙区颗粒与喷射区气体、颗粒之间的横向混合,扩大了喷射区气体对环隙区颗粒运动的影响范围。此外,在相同的进口气体流量条件下,由于多喷嘴喷动-流化床结构分散了进口气体的分布情况,增加了喷射气体的沿程阻力,导致喷动高度较常规喷动床低,由于多喷嘴结构所形成的气流破坏了原来单喷嘴情况所形成的气固喷动床结构,导致气体在喷射区内形成波节形状,改变了颗粒相的运动循环路径,颗粒相在最高处难以形成明显的喷泉区域。
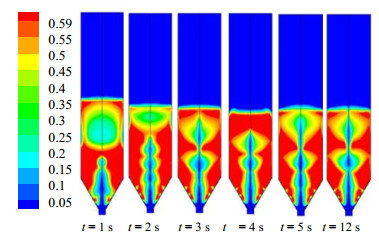
|
图 2 多喷嘴喷动–流化床内颗粒浓度随时间分布情况(U = 1.3Ums) Fig.2 Solid volume fraction as a function of time in the multi-jet spout-fluidized bed |
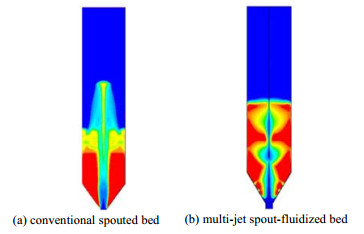
|
图 3 两种喷动床稳定喷动时颗粒浓度分布对比 Fig.3 Comparison of contour plots of solid volume fractions in two spouted beds |
图 4给出了两种喷动床柱锥体部分在不同床层高度下的颗粒体积分数对比情况。由图可知,多喷嘴喷动-流化床的颗粒体积分数分布整体低于常规喷动床,圆锥侧的侧喷嘴设计能有效降低锥体部颗粒体积分数,使得颗粒体积分数沿径向分布变得平缓,有利于消除圆锥处的颗粒流动死区,从而改善了环隙区特别是近圆锥区内颗粒的运动状态。
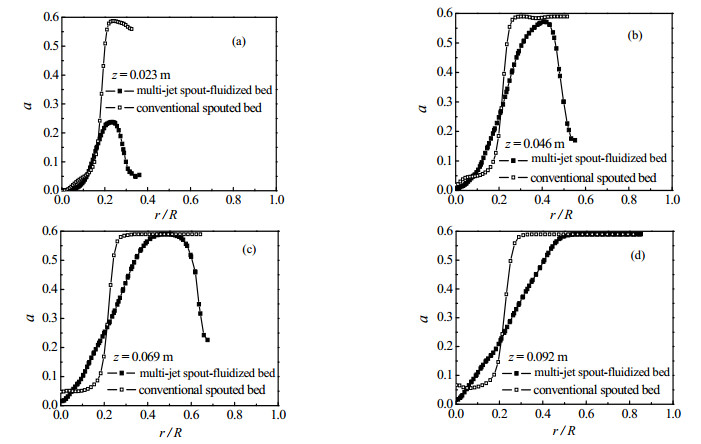
|
图 4 不同床层高度下两种喷动床内颗粒体积分数分布对比 Fig.4 Comparison of particle concentration in two spouted beds |
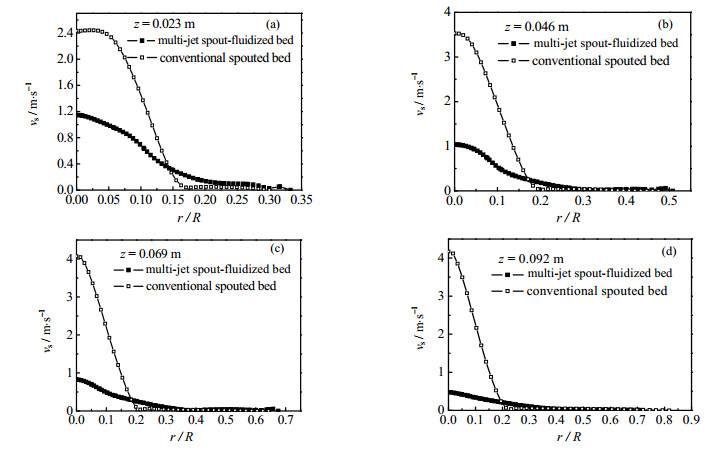
图 5给出了两种喷动床内颗粒速度在不同床层高度处沿径向的分布曲线。由图可知,多喷嘴喷动-流化床内颗粒速度在喷射区远低于常规喷动床颗粒速度,而在环隙区内颗粒速度则高于常规喷动床情况,颗粒体积分数沿径向呈现更加均匀的分布规律。这是由于两种喷动床在相同的入射气体流量下,整体式多喷嘴喷动-流化床中有一部分气体流量进入侧喷嘴中,使得轴中心喷射区气体速度降低,导致喷射区颗粒速度降低,而进入侧喷嘴的气体流量则强化了环隙区颗粒群运动,增加了环隙区颗粒的速度。
|
图 5 不同床层高度下两种喷动床内颗粒速度径向分布对比 Fig.5 Comparison of particle velocity along radial direction in two spouted beds |
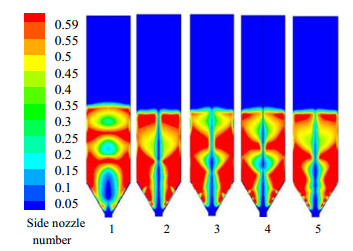
为了全面考察关键设计参数(侧面喷嘴设计参数)对整体式多喷嘴喷动-流化床内气固两相流动的影响规律。考察不同侧喷嘴数量对喷动床中气固两相流体流动的影响规律。设定一个无量纲参数δ/Di为侧喷嘴宽度与主喷嘴直径比值,其中δ为侧喷嘴宽度,Di为喷动床主喷嘴直径。δ/Di在一定程度上给出了侧喷嘴气体流量在喷动床圆锥处的分配情况。给定一个侧喷嘴宽度值为δ/Di= 0.125(侧喷嘴宽度为3 mm,喷动床总入口直径24 mm)。图 6为δ/Di= 0.125 (侧喷嘴宽度3 mm,总入口直径24 mm)时,侧喷嘴数量分别为1,2,3,4,5时喷动床中气固两相流体流动的颗粒浓度分布。由图 6可知,侧喷嘴数量为1时,喷动床中气固两相流体未能形成连续稳定的喷动状态,呈现腾涌现象。而在其他侧喷嘴数量条件下,喷动床中均可形成连续稳定的喷动云图。表明随着侧喷嘴数量的增加,气体在喷动床圆锥处气流分配变得更加均匀,喷动床内环隙区颗粒相循环运动逐渐得到改善,多喷嘴喷动床更容易达到稳定的喷动结构。
|
图 6 侧喷嘴数量对多喷嘴喷动–流化床内颗粒浓度分布影响 Fig.6 Effects of side nozzle number on contour plots of solid volume fraction in the multi-jet spout-fluidized bed |
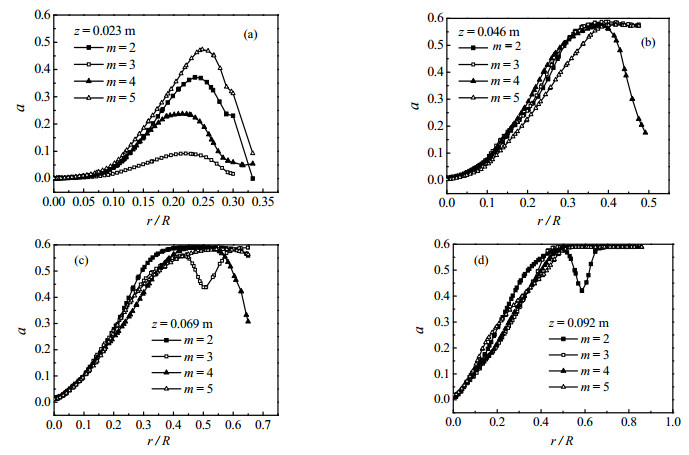
图 7为不同床层高度条件下,侧喷嘴数量对多喷嘴喷动-流化床内颗粒体积分数沿径向分布的影响。由图可知,喷动床内颗粒体积分数整体沿径向呈现出先增大后逐渐减小的趋势,即在床壁处出现了颗粒体积分数局部下降趋势。这是由于床壁处侧喷嘴中气体分流对原有颗粒的分层运动起到了扰动与破坏作用,使得颗粒群沿径向出现了重新分布与均匀化趋势,减小了当地的颗粒体积分数。当z = 0.023 m时(图 7(a)),即低床层高度处,侧喷嘴数量对环隙区颗粒体积分数分布的影响最为显著,环隙区颗粒体积分数随着侧喷嘴数量的增加呈现出先降低后上升现象,即颗粒体积分数分布随侧喷嘴数量呈现出非线性变化规律。随着床层高度的增加,环隙区颗粒距离侧喷嘴距离逐渐增加,侧喷嘴数量对环隙区颗粒体积分布的影响逐渐减弱。总体而言,侧喷嘴数量为3时,环隙区颗粒体积分数沿径向最为均匀,表现出最佳颗粒分布状态。综合图 6和7表明:圆锥处侧喷嘴数量为3时多喷嘴喷动-流化床的整体颗粒体积分布及颗粒速度分布达到了最优状态。
|
图 7 侧喷嘴数量对多喷嘴喷动-流化床内颗粒体积分数径向分布的影响 Fig.7 Effects of side nozzle number on particle concentrations along radial direction of the multi-jet spout-fluidized bed |
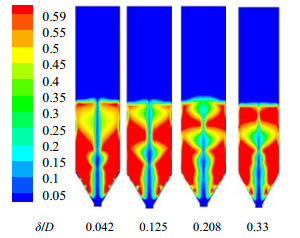
在多喷嘴喷动-流化床锥体侧喷嘴数量不变的情况下,进一步分析侧喷嘴宽度对多喷嘴喷动-流化床圆锥处内气固两相流动的影响规律,设定侧喷嘴数量为3,多喷嘴喷动-流化床的主喷嘴直径设定为24 mm,δ/Di分别设定为0.042、0.125、0.208及0.33 (侧喷嘴宽度分别设计为1、3、5及8 mm)。在稳定喷动情况下,多喷嘴喷动-流化床内颗粒体积分布如图 8所示。由图 8知,喷射区的影响范围随着侧喷嘴数量的增加而逐渐增大,表明侧喷嘴数量的增加有利于增加气固接触与混合程度,但另一方面也增加了喷射气体的流动阻力。当无量纲侧喷嘴宽度δ/Di增大到一定程度时(0.33),即气固接触阻力增加到一定程度,多喷嘴喷动-流化床中气流不能将颗粒带动至静床层高度顶部,从而导致多喷嘴喷动-流化床内不能形成正常而稳定的喷动结构,欲改善喷动状态则需进一步增加进口气体流速。
|
图 8 侧喷嘴宽度对喷动–流化床内颗粒体积分数云图影响 Fig.8 Effects of width of side nozzle on contour plots of solid volume fractions in the multi-jet spout-fluidized bed |
图 9为在不同床层高度处,无量纲侧喷嘴宽度对多喷嘴喷动-流化床内颗粒体积分数沿径向分布的影响规律。由图可知,在低床层高度处(z = 0.023 m),颗粒体积分数随着侧喷嘴宽度的增加呈现出先降低后上升现象,无量纲侧喷嘴宽度δ/Di= 0.125 (宽度为3 mm)时,颗粒体积分数沿径向分布的均匀度最好。随着床层高度的增加,侧喷嘴宽度的增加使得多喷嘴喷动床椎体部颗粒局部流化效果更好,整体上有利于降低颗粒体积分数径向分布,有利于实现颗粒体积分数径向分布均匀化。
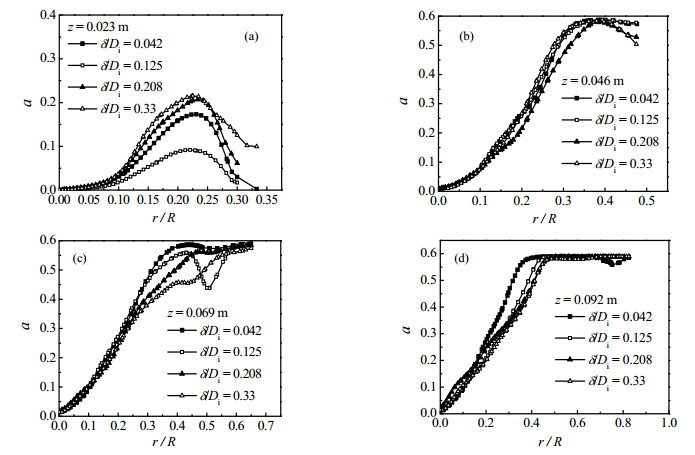
|
图 9 侧喷嘴宽度对多喷嘴喷动–流化床内颗粒体积分数径向分布影响 Fig.9 Effects of width of side nozzle on particle concentration along radial direction of the multi-jet spout-fluidized bed |
(1) 采用双流体模型(TFM)对整体式多喷嘴喷动-流化床内的气固两相流动特性进行了数值模拟,相比较于常规柱锥喷动床,整体式多喷嘴喷动-流化床不仅能够在床体圆锥处产生颗粒局部流态化效果,有效消除喷动床锥体区的颗粒流动死区,强化喷动床内喷射区及环隙区内气体、颗粒的两相径向混合与运动,而且能够省略旁路供气辅助设备。通过CFD数值模拟证明了整体式多喷嘴喷动-流化床结构在改善喷动床环隙区内颗粒运动状态的可行性。
(2) 多喷嘴喷动-流化床近壁面处颗粒速度值随着床层高度的增加而增加。侧喷嘴中的气体分流对原有颗粒的分层运动起到了扰动与破坏作用,使得多喷嘴喷动-流化床内颗粒群浓度沿径向出现了重新分布及均匀化趋势,在喷动-流化床圆锥体处,侧喷嘴数量对环隙区颗粒体积分数分布的影响最为显著。侧喷嘴数量为3时,环隙区颗粒整体体积分数沿径向最为均匀,表现出最佳的颗粒径向均匀化分布。
(3) 在低床层高度处,颗粒体积分数随着侧喷嘴宽度的增大呈现出先降低后上升的非线性变化规律,无量纲侧喷嘴宽度δ/Di= 0.125 (宽度为3 mm)时,颗粒体积分数沿径向分布的均匀度最好。随着床层高度的增加,侧喷嘴宽度的增加整体上有利于颗粒体积分数径向分布均匀化。
(4) 可进一步研究分析进口气体流量、颗粒物性尺寸设计参数、气体物性设计参数等因素对整体式多喷嘴喷动-流化床内气固两相流动特性的影响规律。
符号说明:
| CD | —曳力系数 | Ums | —最小总入口气体喷动速度,m·s-1 |
| D | —喷动床柱体直径,mm | U | —总入口气体喷动速度,m·s-1 |
| Di | —总气体入口直径,mm | v | —气体或颗粒速度矢量,m·s-1 |
| dP | —颗粒直径,mm | x, y, z | —坐标轴,m |
| g | —重力加速度 | z | —床层高度,m |
| H0 | —固定床高,m | ε | —气体或颗粒浓度 |
| i | —气体或者颗粒相 | εs | —颗粒浓度 |
| kgs | —相间动量传递系数 | εs, max | —颗粒最大填充浓度 |
| m | —侧喷嘴数量 | α | —颗粒体积分数 |
| Pg | —气体压力,Pa | βg | —气体-颗粒相间曳力系数 |
| R | —喷动床柱体半径,mm | ρ | —流体密度,kg·m-3 |
| Res | —相对雷诺数 | μg | —气体黏度,Pa·s |
| r | —喷动床径向距离,mm | τg | —气体应力张量 |
| t | —时间,s | τs | —颗粒应力张量 |
| ums | —最小表观气速,m·s-1 | δ | —侧喷嘴宽度,mm |
| [1] | ZHAO Yong-zhi(赵永志), CHENG YI(程易), JIN Yong(金涌). Kinetic simulation of two-dimensional spouted bed with draft plates by discrete element method(二维导流管喷动床离散颗粒动力学模拟)[J]. Chemical Engineering(化学工程) , 2007, 35(6): 24-28. |
| [2] | HU Guo-xin(胡国新), LU Xiao-ling(陆晓玲), GONG Xi-wu(龚希武), et al. Experimental study on particles spouting characteristics in a novel annular spouted bed(新颖环形喷动床颗粒喷动特性实验研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2007, 21(6): 936-941. |
| [3] | ZHANG Shao-feng(张少峰), LI Ling-mi(李玲密), WANG Jin-gang(王晋刚), et al. Experimental research of semi-dry flue gas simultaneous desulfurization and denitrification with spouted bed(喷动床半干式烟气脱硫脱硝实验研究)[J]. Chinese Journal of Environmental Engineering(环境工程学报) , 2011, 5(8): 1847-1851. |
| [4] | ZHU Wei-bing(朱卫兵), XING Li-chao(邢力超), SUN Qiao-qun(孙巧群), et al. Numerical simulation of flue gas desulfurization in a spouted bed based on two-fluid model(基于双流体模型的烟气喷动床脱硫过程的数值模拟)[J]. Journal of China Mining University(中国矿业大学学报) , 2012, 41(1): 7-13. |
| [5] | HE Yu-rong(何玉荣), SUN Qiao-qun(孙巧群), LU Hui-lin(陆慧林), et al. Gas-solid flow simulations in spouted beds on body-fitted coordination(贴体坐标系下喷动床内气固两相流体动力特性的数值模拟)[J]. Journal of Combustion Science and Technoly(燃烧科学与技术) , 2006, 12(1): 59-64. |
| [6] | JIN Yong(金涌), ZHU Jing-xu(祝京旭), WANG Zhan-wen(汪展文), et al. Fluidization engineering principles(流态化工程原理)[M].Beijing(北京): Tsinghua University Press(清华大学出版社), 2001. |
| [7] | Wang S Y, Zhao L Q, Wang C S, et al. Numerical simulation of gas-solid flow with fluid model in a spouted-fluid bed[J]. Particuology , 2014, 149(3): 109-116. |
| [8] | WU Feng (吴峰), ZHANG Xuan (张旋), SHANG Lin-yi (尚灵祎), et al. An integral multi-nozzle structure of spouted-fluidized bed (一种喷动-流化床的整体式多喷嘴结构): CN, 201520886451. X[P]. 2016-02-04. |
| [9] | Wang Q, Luo J L, Xu C H. Numerical simulation of the gas-particle flow behavior in oil shale semi-coke spouted bed[J]. Energy Procedia , 2012, 17: 892-900. DOI:10.1016/j.egypro.2012.02.184. |
| [10] | Liu X J, Shao Y J, Zhong W Q, et al. Prediction of minimum spouting velocity by CFD-TFM:approach development[J]. Canadian Journal of Chemical Engineering , 2013, 91(11): 1800-1808. |
| [11] | Lan X, Xu C, Gao J, et al. Influence of solid-phase wall boundary condition on CFD simulation of spouted beds[J]. Chemical Engineering Science , 2012, 69(1): 419-430. DOI:10.1016/j.ces.2011.10.064. |
| [12] | Yang S L, Luo K, Zhang K, et al. Numerical study of a lab-scale double slot-rectangular spouted bed with the parallel CFD-DEM coupling approach[J]. Powder Technology , 2015, 272: 85-99. DOI:10.1016/j.powtec.2014.11.035. |
| [13] | Wang S Y, Shao B, Liu R, et al. Comparison of numerical simulations and experiments in conical gas-solid spouted bed[J]. Chinese Journal of Chemical Engineering , 2015, 23(10): 1579-1586. DOI:10.1016/j.cjche.2015.07.006. |
| [14] | Hosseini S H, Fattahi M, Ahmadi G. Hydrodynamics studies of a pseudo 2D rectangular spouted bed by CFD[J]. Powder Technology , 2015, 279: 301-309. DOI:10.1016/j.powtec.2015.04.013. |
| [15] | Qiu K Z, Hu C S, Yang S L, et al. Computational evaluation of depth effect on the hydrodynamics of slot-rectangular spouted bed[J]. Powder Technology , 2016, 287: 51-60. DOI:10.1016/j.powtec.2015.09.034. |
| [16] | Hosseinia S H, Fattahi M, Ahmadi G. CFD study of hydrodynamic and heat transfer in a 2D spouted bed:assessment of radial distribution function[J]. Journal of the Taiwan Institute of Chemical Engineers , 2016, 58: 107-116. DOI:10.1016/j.jtice.2015.06.027. |
| [17] | REN Li-bo(任立波), HAN Ji-tian(韩吉田), HE Hai-lan(何海澜). Parallel computing of discrete particle flows based on information communication model of FLUENT platform(基于FLUENT软件信息传递模式的离散颗粒流动的并行算法)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2015, 29(4): 963-970. |
| [18] | He Y L, Qin S Z, Lim C J, et al. Particle velocity profiles and solid flow patterns in spouted beds[J]. Canadian Journal of Chemical Engineering , 1994, 72(4): 561-568. DOI:10.1002/cjce.v72:4. |
| [19] | He Y L, Lim C J, Grace J R, et al. Measurements of voidage profiles in spouted beds[J]. Canadian Journal of Chemical Engineering , 1994, 72(2): 229-234. DOI:10.1002/cjce.v72:2. |
| [20] | WU Feng(吴峰), ZHANG Jie-jie(张洁洁), NIU Fang-ting(牛方婷), et al. Numerical study of turbulence model effect on gas-particle flow behavior in spouted bed(湍流模型对喷动床内气、固相流动特性的影响)[J]. China Sciencepaper(中国科技论文) , 2015, 10(24): 2909-2914. DOI:10.3969/j.issn.2095-2783.2015.24.019. |




