2. 昆明理工大学 云南省有色金属真空冶金重点实验室, 云南 昆明 650093;
3. 昆明理工大学 云南省先进电池及材料工程实验室, 云南 昆明 650093
2. Key Laboratory for Nonferrous Vacuum Metallurgy of Yunnan Province, Kunming University of Science and Technology, Kunming 650093, China;
3. Engineering Laboratory for Advanced Batteries and Materials of Yunnan Province, Kunming University of Science and Technology, Kunming 650093, China
硫酸亚铁作为硫酸法生产钛白粉过程中的工业副产物,广泛存在于化工、冶金等领域。中国是钛白粉生产大国,目前有50余家生产企业,每年副产的七水硫酸亚铁约250万吨,因其含有多种杂质, 不能直接利用,随意堆放既严重污染了环境,又浪费了资源[1]。当前,处理硫酸亚铁的方法主要有以下几种[2]:直接利用作为土壤改良和农业废料及药剂或作为污水处理剂及自来水的净化剂;制造氧化铁颜料系列(铁黄、铁红、铁黑等);制造磁性氧化铁材料等。除此之外,随着锂离子电池的不断发展,草酸亚铁作为合成锂离子电池正极材料磷酸铁锂的原料,引起了人们的广泛关注[3, 4]。若能将钛白副产硫酸亚铁作为原料制备电池级草酸亚铁,既解决了副产硫酸亚铁的处理问题,又能满足电池行业的发展需求。钛白粉制造过程中副产的硫酸亚铁纯度较低,杂质含量高,如对硫酸亚铁不处理,则合成的草酸亚铁纯度对后续磷酸铁锂正级材料的比容量和循环性能有非常大的影响[5]。攀枝花地区钛白副产硫酸亚铁中锰、镁、镍、锌等杂质含量都较高,这些杂质的存在势必会对制备草酸亚铁的纯度造成一定影响。因此,如果用于合成电池级草酸亚铁,则必须对副产硫酸亚铁进行提纯处理。结晶法作为一种重要的分离、提纯方法,广泛应用于食品、精细化工和制药工业[6~9],但有关结晶法提纯副产硫酸亚铁的系统研究鲜有报道。
本文采用结晶法对副产硫酸亚铁进行提纯,并通过建立该过程的数学模型,预测杂质走向,最后通过实验验证此数学模型的可靠性。
2 实验部分 2.1 实验装置WB2000-M变频电动搅拌器(德国WIGGENS公司)-主要用于加速硫酸亚铁溶解和结晶;低温恒温槽(DC-3006上海衡平仪器仪表厂)-主要用于溶液的加热与降温结晶;2XZ-4型旋片真空泵(上海真空泵厂)-主要用于抽滤分离溶液和晶体;电热鼓风干燥箱(101-3型沪南实验仪器厂)-主要用于所得晶体的干燥;AAS(WFX-320型火焰原子分光光度计,北京瑞利分析仪器公司)-主要用于测定所得晶体中各杂质元素的含量。
2.2 实验原料实验中采用的硫酸亚铁为四川攀枝花某钛白粉厂硫酸法生产钛白粉过程中的副产物,其部分杂质含量采用原子吸收分光光度计(AAS)测定,结果见表 1所示。
| 表 1 副产硫酸亚铁中杂质含量 Table 1 Impurity concentration in ferrous sulfate |
将原料硫酸亚铁置于烧杯中,加入一定量的去离子水,加热至指定温度,待物料溶解完全,再将溶液降温到一定温度,充分结晶后,抽滤分离得到硫酸亚铁晶体。多次结晶重复以上步骤即可。结晶产物于鼓风干燥箱中烘干待测。
3 结晶提纯的数学模型 3.1 理论基础结晶的数学模型是针对结晶动力学建立的,主要是成核速率模型和生长速率模型。当前,关于晶体纯度预测模型的报道还很少,晶体纯度预测模型不仅可以用来预测产品纯度,而且还可以用来指导结晶器和结晶工艺的设计和开发。因此,建立晶体纯度预测模型,具有非常重要的意义。
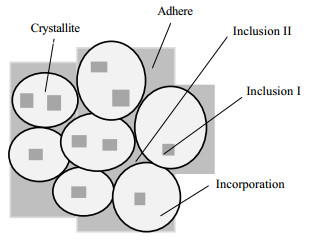
目前,结晶提纯数学模型建立主要有两个方向,一种是在多次结晶过程中假设每次杂质在晶体与母液之间的分配系数不变,进而推导其数学模型[10];另一种是假设每次杂质在母液与晶体之间传质的扩散系数不变,进而推导其数学模型。本文根据第二种假设,首先讨论结晶过程中杂质的残留,König A等[11]认为在结晶过程中杂质主要为四种,分别是:晶体外溶液的黏附、晶体内溶液的夹杂、晶核和晶体表面的附着以及晶体之间溶液的掺杂,如图 1所示。晶体与溶液的分离过程主要影响晶体外溶液与晶体之间溶液中杂质浓度的大小;而结晶过程则决定了杂质在晶体内溶液与晶体内浓度的大小。根据以上分析,本研究中杂质的残留主要由结晶过程决定。
|
图 1 杂质残留 Fig.1 Impurity segmentation |
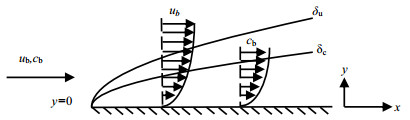
ha Z L等[12]在研究溶液黏度对结晶提纯的影响时,曾提出基于边界层理论的结晶提纯模型,认为晶体表面处杂质的浓度是由边界层理论决定。如图 2所示,在搅拌条件下结晶,当溶液中杂质向晶体表面传质时,强制对流在晶体表面附近消失,整个传质主要集中在边界层厚度为δ的晶体表面,且晶体与溶液之间的边界层处于平衡状态[13~15]。因此,边界层处杂质扩散可做出以下假设[16~19]:
|
图 2 晶体表面的浓度边界层与速度边界层 Fig.2 Concentration and velocity boundary layers of crystal surface |
(1) 结晶条件相同时,晶体表面杂质浓度边界层梯度不变,则传质系数kd与扩散流密度J为常数。
(2) 溶液均为饱和溶液,且杂质残留均匀,则黏度的雷诺准数Re与施密特准数Sc均不变,即有效边界层厚度不变。
(3) 忽略杂质对固液相平衡的影响,且认为结晶过程也不影响杂质在边界层的扩散。
3.2 数学模型的建立根据结晶过程杂质残留的存在方式,并结合边界层理论与菲克定律提出了钛白副产硫酸亚铁结晶提纯的数学模型。参考王保明等[10]对磷酸结晶提纯数学模型推导中对于已知物料第n次结晶过程进行的物料衡算和杂质衡算,可得:
| $ {M_{{\rm{c}},n - 1}} + {M_{{{\rm{H}}_{\rm{2}}}{\rm{O}},n - 1}} = {M_{1n}} + {M_{c,n}} $ | (1) |
| $ {M_{{\rm{c}},n - 1}}{x_{i{\rm{c, }}n{\rm{ - 1}}}} = {M_{{\rm{c}},n}}{x_{i{\rm{c}},n}} + {M_{l,n}}{x_{{\rm{il,}}n}}$ | (2) |
由于每次稀释都要保证得到的均为饱和溶液,即表示为:
| $ \left( {{M_{{\rm{c,}}n{\rm{ - 1}}}} + {M_{{{\rm{H}}_{\rm{2}}}{\rm{O}},n - 1}}} \right){x_{\rm{d}}} = {M_{{\rm{c,}}n - 1}}{x_{{\rm{c}},n - 1}} $ | (3) |
式中,xc, n-1,xd为n-1次结晶晶体中七水硫酸亚铁的浓度和结晶物料所需的七水硫酸亚铁的浓度。
令:
| $ d = \left( {{M_{{{\rm{H}}_{\rm{2}}}{\rm{O,}}n{\rm{ - 1}}}} + {M_{{\rm{c,}}n - 1}}} \right)/{M_{{\rm{c}}n - 1}} = {x_{_{{\rm{c}}n - 1}}}/{x_{\rm{d}}} $ | (4) |
将式(1)代入式(2),并联立式(4)整理得:
| $ {x_{i{\rm{l}},n}} = \frac{{{x_{i{\rm{c}},n - 1}}/d - {x_{i{\rm{c}},n}}{M_{c,n}}/({M_{{\rm{c}},n - 1}} + {M_{{{\rm{H}}_{\rm{2}}}{\rm{O}},n - 1}})}}{{1 - {M_{{\rm{c}},n}}/({M_{{\rm{c}},n - 1}} + {M_{{{\rm{H}}_{\rm{2}}}{\rm{O}},n - 1}})}} $ | (5) |
由于每次结晶过程,冷却速率、结晶终温、搅拌速度都是一定的,因此,一定浓度的七水硫酸亚铁结晶的晶体收率是一定的,为常数。
| $ y = \frac{{{M_{{\rm{c}},n}}}}{{{M_{{\rm{c}},n - 1}} + {M_{{{\rm{H}}_{\rm{2}}}{\rm{O}},n - 1}}}} $ | (6) |
将(6)式代入(5)式,可得:
| $ {x_{i{\rm{l}},n}} = \frac{{{x_{i{\rm{c}},n - 1}}/d - {x_{i{\rm{c}},n}}y}}{{1 - y}} $ | (7) |
如图 2,取一个晶粒为研究对象,在强制对流条件下,在晶体表面的边界层处会同时出现速度边界层和浓度边界层[14]。在晶体和流体界面附近的传质过程,用杂质在界面处的扩散流密度表示,则在晶体界面与溶液内部此杂质存在以下分布方程:
| $ J = {{\rm{k}}_{\rm{d}}}({c_{{\rm{s}},n}} - {c_{{\rm{b}},n}}) $ | (8) |
由杂质质量浓度与物质量浓度直接的换算关系,可得:
| $ {c_{{\rm{s}},n}} = \frac{{{x_{i{\rm{l}},n}}{\rho _{l,n}}}}{M},{c_{{\rm{b}},n}} = \frac{{{x_{i{\rm{c}},n}}{\rho _{{\rm{c,}}n}}}}{M}$ | (9) |
令:
| $ \frac{{{\rho _{{\rm{l}},n}}}}{M} = a,\frac{{{\rho _{{\rm{c}},n}}}}{M} = b$ | (10) |
将式(10)代入式(9)和式(8),并联立式(7),可得:
| $ {x_{i{\rm{c}},n}} = \frac{{ - a{x_{i{\rm{c}},n - 1}} + \frac{{J(1 - y)d}}{{{k_{\rm{d}}}}}}}{{(by - b - ay)d}} $ | (11) |
令:
| $ p = \frac{{ - a}}{{(by - y - ay)d}},q = \frac{{J(1 - y)}}{{{k_{\rm{d}}}(by - y - ay)}} $ | (12) |
将式(12)代入式(11),简化可得:
| $ {x_{i{\rm{c}},n}} = q + p{x_{i{\rm{c}},n - 1}} $ | (13) |
式中,p定义为杂质元素的脱除系数,并根据此前分析可知p与q均为常数,因此式(13)便转化为数列求通项公式的问题,解得:
| $ {x_{i{\rm{c}},n}} = ({x_{i{\rm{c}},1}} - {x_{i{\rm{c}},0}})\frac{{(1 - {p^n})}}{{1 - p}} + {x_{i{\rm{c}},0}}\left( {n \ge 1} \right) $ | (14) |
| $ {x_{i{\rm{c}},n}} = ({x_{i{\rm{c}},0}}p + q - {x_{i{\rm{c}},0}})\frac{{(1 - {p^n})}}{{1 - p}} + {x_{i{\rm{c}},0}}\left( {n \ge 1} \right) $ | (15) |
式(14)、(15)便是经过n次结晶后杂质残留的基本方程,即为结晶提纯过程中杂质残留的预测模型。将式(14)两边取对数,后可得式(16):
| $ n\ln p + \ln ({x_{i{\rm{c}},0}} - {x_{i{\rm{c}},1}}) = {\rm{ln}}\left[ {\left( {{x_{i{\rm{c}},0}} - {x_{ic,1}}} \right) - \left( {1 - p} \right)\left( {{x_{i{\rm{c}},0}} - {x_{i{\rm{c}},n}}} \right)} \right]\left( {n \ge 1} \right) $ | (16) |
通过式(16)可以看出:在半对数坐标系中,晶体中杂质浓度随结晶次数呈线性分布。
4 结果与讨论通过对结晶提纯数学模型的分析,定义p为杂质的脱除系数,其决定了结晶过程中不同杂质的脱除率。当0 < p < 1时,说明可通过重结晶的方式提纯,且p值越小表示杂质的脱除率越高,提纯效果越好;反之,若p≥1时,则表示不能通过此方式提纯。本实验考察了四种杂质元素(Ni、Zn、Mn、Mg)在结晶过程中含量的变化。通过一次结晶实验计算得到各杂质元素的脱除系数p,结果见表 2,由此可知利用结晶法提纯副产硫酸亚铁是可行的,且验证了此物料在结晶提纯过程中杂质的存在方式为晶粒表面的逐层富集。
| 表 2 不同杂质在结晶过程中的脱除系数 Table 2 Edulcoration coefficients of different impurities during crystallization |
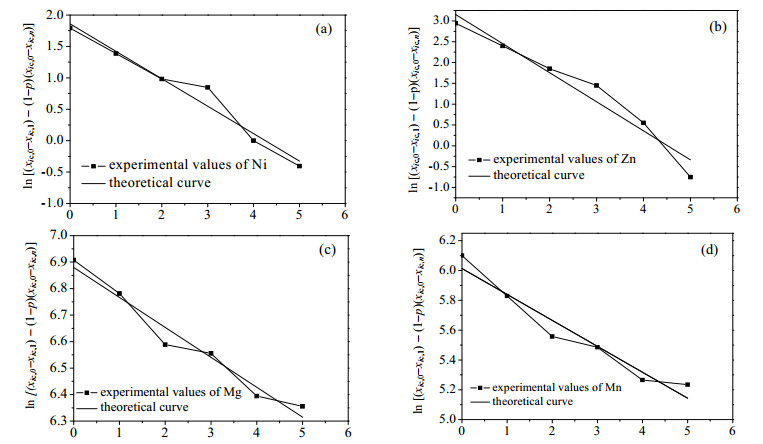
在相同条件下,进行了5次结晶实验,考察结晶次数对杂质含量的影响。将每次结晶产物中杂质元素(Ni、Zn、Mn、Mg)的含量代入(16)式拟合,结果如图 3和表 3所示。由各元素的拟合曲线结果可以看出,结晶物料中各元素含量的相应关系式计算结果与结晶次数呈现良好的线性关系,表明了该结晶模型适用于预测副产硫酸亚铁结晶提纯过程中Ni、Zn、Mn、Mg四种杂质元素的变化。
|
图 3 结晶次数对各杂质的影响 Fig.3 Effects of crystallization time on impurities (a) Ni (b) Zn (c) Mg (d) Mn |
| 表 3 各元素拟合曲线的线性相关系数 Table 3 Linear correlation coefficients of the fitting curves for each element |
从图 3可以看出,四种杂质元素的脱除速率在第三次结晶后整体呈现逐渐减小,后增加的趋势,致使图 3中的各点稍有偏离理论的线性关系。究其原因,一方面由于在一定的实验条件下,结晶的净化能力是有限的,当杂质的浓度接近极限浓度时,杂质的脱出速率减缓;另一方面由于溶液中杂质浓度的降低会导致固-液边界层中杂质浓度梯度的变化,从而影响杂质离子的扩散与分布。但从图中也可以看出,这种变化并没有过多的导致各杂质走向严重偏离相对理论线性关系。因此,仍可以认为各杂质离子在边界层处的扩散系数保持不变,由此推导出的提纯模型仍有很好的预测准确性。
由表 3对比各元素的拟合曲线,Zn、Ni的线性关系较Mn、Mg更好一些,这说明基于边界层传质理论推导出来的结晶提纯模型,更适合杂质含量低的元素。分析其原因,是由于低含量杂质在多次结晶中固液边界层中浓度梯度的变化较小,从而对杂质脱除系数p的影响较小,线性关系也就更好。这也进一步说明在结晶过程中,杂质离子是通过固液边界层由液相进入结晶体表面的。
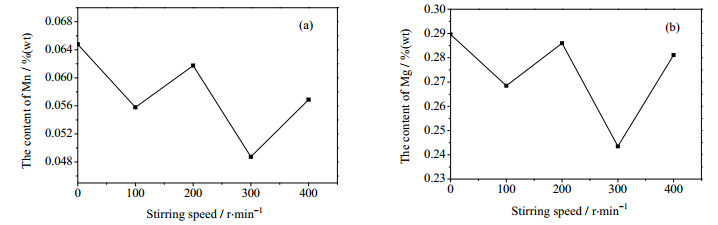
4.2 结晶过程搅拌速率对杂质含量的影响由于在结晶过程中,搅拌速率对晶体的成核与生长,以及晶体的形态与结构有很大的影响[20~22],进而也会影响杂质的残留。为了进一步验证结晶过程中杂质离子是通过固液边界层扩散传质进入晶体,分别进行了不同搅拌速率下一次结晶提纯的实验研究。由于Ni、Zn含量较少,考虑到搅拌对其影响较小,并未进行讨论,实验结果如图 4所示。
|
图 4 搅拌速率对各杂质的影响 Fig.4 Effects of stirring on impurities (a) Mn (b) Mg |
从图 4可以看出,随着搅拌速率的逐渐增大,杂质含量整体呈现起伏式降低的趋势。分析其原因,一方面,搅拌可以减小离子的扩散激活能,加速离子的扩散[23],同时,搅拌强度增大时可减小晶粒表面附近液体层厚度,即可减小离子扩散的边界层厚度,促进了杂质离子从溶液向晶体的扩散;但另一方面,搅拌也阻止聚结体的生成,保证生长条件比较一致,进而细化晶粒[24, 25],从而减少了晶粒团聚过程中杂质离子的引入。因此,杂质的残留情况受到搅拌速率不同方向的影响,而呈现出不规则的变化。
通过以上的分析可知,搅拌影响了晶体的生长,在各因素的影响下改变了杂质在晶体与溶液间边界层中的浓度梯度,也验证了杂质离子在结晶过程中是通过固液边界层扩散传质进入晶体。
5 结论(1) 采用多次结晶的方法,可以提纯钛白副产硫酸亚铁,有效去除杂质,也验证了结晶过程中杂质的残留方式;
(2) 搅拌速率改变了杂质在晶体与溶液间固液边界层的浓度梯度,影响了晶体的生长和杂质的残留,验证了在结晶过程中杂质离子是通过固液边界层扩散传质进入晶体的;
依据固液边界层传质理论,推导出了结晶提纯模型,为改进实验条件提供了理论依据。通过多次结晶提纯实验验证了结晶提纯模型的可靠性,该模型能较好地预测杂质浓度,尤其是含量较低的杂质,为优化结晶提纯工艺提供了理论指导。
符号说明:| [1] | PENG Ai-guo(彭爱国), HE Zhou-chu(贺周初), YU Chang-yan(余长艳) . Research on preparation of battery-grade ferrous oxalate from the byproduct ferrous sulfate(副产硫酸亚铁制备电池级草酸亚铁的研究)[J]. Inorganic Chemicals Industry(无机盐工业) , 2012, 8 (44) : 60-62 |
| [2] | PU Gui-bing(蒲贵兵), SUN Ke-wei(孙可伟) . Complicated analysis and usage of the vice-product FeSO4 in the process of titanium powders by H2SO4(硫酸法钛白副产硫酸亚铁的综合利用)[J]. China Resources Comprehensive Utilization(中国资源综合利用) , 2007, 7 (25) : 12-14 |
| [3] | Yang S F, Peter Y Z, Stanley W M . Hydrothermal synthesis of lithium iron phosphate cathodes[J]. Electrochemistry Communication , 2001, 3 (9) : 505-508 DOI:10.1016/S1388-2481(01)00200-4 |
| [4] | WU Jian(吴鉴), YAO Yao-chun(姚耀春), LONG Ping(龙萍) . Preparation of ferrous oxalate powder as raw material of Li-ion battery(锂离子电池原材料草酸亚铁粉体的制备)[J]. Powder Metallurgy Technology(粉末冶金技术) , 2013, 31 (6) : 439-440 |
| [5] | Jugović D, Uskoković D . A review of recent developments in the synthesis procedures of lithium iron phosphate powders[J]. Journal of Power Sources , 2009, 190 (2) : 538-540 DOI:10.1016/j.jpowsour.2009.01.074 |
| [6] | Shiau L D, Zeng S L . Separation of the catechol/4-methoxyphenol mixture by stripping crystallization[J]. Journal of Industrial & Engineering Chemistry , 2012, 18 (3) : 963-968 |
| [7] | Nie Q, Wang J K, Yin Q . Effect of solution thermodynamics on the purification of two isomorphic steroids by solution crystallization[J]. Chemical Engineering Science , 2006, 61 (18) : 5962-5963 DOI:10.1016/j.ces.2006.05.018 |
| [8] | WU Jun(吴俊), HUANG Min(黄民), GUO Si-si(郭思斯) . Optimization of xylol continuous suspension crystallization process with two separate feed streams(双进料混合二甲苯连续悬浮结晶工艺的优化)[J]. J Chem Eng of Chinese Univ(高校化学工程学报) , 2010, 24 (4) : 705-706 |
| [9] | Kim Y N, Lee J Y, Kim J H . Improvement of a crystallization process for the purification of vancomycin[J]. Process Biochemistry , 2011, 46 (10) : 2068-2073 DOI:10.1016/j.procbio.2011.07.020 |
| [10] | WANG Bao-ming(王保明), LI Jun(李军), QI Ya-bing(齐亚兵) . Numerical model and experiments for purification of phosphoric acid by crystallization(结晶法提纯工业磷酸的数学模型与实验研究)[J]. J Chem Engof Chinese Univ(高校化学工程学报) , 2012, 26 (2) : 204-206 |
| [11] | König A, Schreiner A . Purification potential of melt crystallization[J]. Powder Technology , 2001, 121 (1) : 88-89 DOI:10.1016/S0032-5910(01)00379-5 |
| [12] | Sha Z L, Alatalo H, Louhi-Kultanen M . Purification by crystallization from solutions of various viscosities[J]. Journal of crystal growth , 1999, 198-199 (3) : 692-696 |
| [13] | ZHENG Ping-you(郑平友), CHEN Xiao-yan(陈孝彦), CUI Zhao-yang(崔朝阳) . Study of mass transfer law in forced inner circulation evaporative crystallization system(强制循环蒸发结晶中传质规律的研究)[J]. Journal of Xi'an Jiaotong University(西安交通大学学报) , 2003, 37 (11) : 1194-1195 |
| [14] | Derksen J J . Simulations of solid-liquid mass transfer in fixed and fluidized beds[J]. Chemical Engineering Journal , 2014, 255 (7) : 233-234 |
| [15] | HUA Yi-xin(华一新) . Kinetics of metallurgical process(冶金过程动力学导论)[M]. Beijing(北京): Metallurgical Industry Press(冶金工业出版社), 2004 : 101 -114. |
| [16] | YUAN Jun-sheng(袁俊生), WANG Yu(王瑜), LIU Yan-lan(刘燕兰) . Model of transfer and crystal growth rate in cycling-fluidized crystallization(循环流化结晶过程传质与晶体生长速率模型)[J]. J Chem Ind and Eng(China)(化工学报) , 2001, 52 (11) : 982-983 |
| [17] | XIA Shao-jun(夏少军), CHEN Lin-gen(陈林根), SUN Feng-rui(孙丰瑞) . Entransy dissipation minimization for isothermal crystallization processes with diffusive mass transfer law(扩散传质定律等温结晶过程积耗散最小化)[J]. Journal of Mechanical Engineering(机械工程学报) , 2013, 49 (24) : 175-176 DOI:10.3901/JME.2013.24.175 |
| [18] | Schlichting H. Boundary-layer theory(边界层理论)[M]. Beijing(北京):Science Press(科学出版社), 1988:26-28. |
| [19] | Adrover A, Pedacchia A . Mass transfer through laminar boundary layer in microchannels with nonuniform cross section:The effect of wall shape and curvature[J]. International Journal of Heat & Mass Transfer , 2013, 60 (5) : 624-625 |
| [20] | Kouchi A, Tsuchiyama A, Sunagawa I . Effect of stirring on crystallization kinetics of basalt:texture and element partitioning[J]. Contributions to Mineralogy and Petrology , 1986, 93 (4) : 435-437 |
| [21] | Yan F W, Zhang S F, Guo C Y . Influence of stirring speed on the crystallization of calcium carbonate[J]. Crystal Research and Technology , 2009, 44 (7) : 725-728 DOI:10.1002/(ISSN)1521-4079 |
| [22] | YANG Chen(杨晨), SONG Xing-fu(宋兴福), WANG Jin(汪瑾) . Reactive crystallization process of hydromagnesite microspheres(碱式碳酸镁微球的反应结晶过程)[J]. J Chem Ind and Eng(China)(化工学报) , 2013, 2 (64) : 719-722 |
| [23] | SU Yu-chang(苏玉长), CHEN Hong-yan(陈宏艳), HU Ze-xing(胡泽星) . Synthesis and microstructure of ferrous oxalate dehydrate of different dimensionalities(不同维度草酸亚铁的合成及其组织结构)[J]. Journal of central south university(中南大学学报) , 2013, 44 (6) : 2240-2241 |
| [24] | Хамский E B. Crystallization in the chemical industry(化学工业中的结晶)[M]. Beijing(北京):Chemical Industry Press(化学工业出版社), 1984:45-59. |
| [25] | Veintemillas-Verdaguer S, Esteban S O, Herrero M A . The effect of stirring on sodium chlorate crystallization under symmetry breaking conditions[J]. Journal of Crystal Growth , 2007, 303 (2) : 562-567 DOI:10.1016/j.jcrysgro.2007.01.014 |




