在诸多现代工业生产如水力、冶金、化工等行业都存在悬浊液处理,其中涉及高浊度水的产生、利用和再处理过程。水体净化中常用处理方式有沉淀过滤法、活性炭吸附法、蒸馏法等,其中沉淀过滤法以成本低廉、见效迅速的优点在世界范围被广泛采用[1-2]。矿业污水中含有大量黏土悬浮颗粒,主要包含高岭土、蒙脱土、膨润土等,较难以自然沉降方式去除,需通过絮凝作用加速沉降[3-4]。高浊度水絮凝沉淀过程特征为生成一条明显的清水-浑水分割线,即浑液面[5]。目前对高浊度水絮凝沉淀的研究,大都以浑液面沉降速度为指标,配合前期在线、后期离线观测和表征来反映过程变化[6]。这样一是无法获取更多详尽的有效信息;二是无法对视野阻挡、溶液含固量接近临界值导致的浑液面较模糊等情况实现精确的在线测量[7-8]。目前针对絮凝沉淀过程的在线测量手段较多,如图像探针、浊度仪、颗粒计数器、透光脉冲等[9-11],但大都需对样品进行一定程度稀释、外部引流或取样,无法做到真正的在线监测[12],只有对高浊度水絮凝沉淀全过程多角度在线测量,才能满足絮凝机理的探索和工艺优化需求,因此迫切需要原理简单、成本低廉、搭建迅速且又能满足原位、非侵入和实时测量的监测手段。超声检测具有抗干扰强、安装灵活的优点,能在光学法不及的浓度上限内进行物料浓度测量,而且不存在安全性顾虑[13]。蔡小舒等对悬浊液的多频超声衰减信号进行分析、算法反演,并通过实验和工业环境下的较高体积分数单分散系颗粒参数测量,获得准确的颗粒粒度和体积分数[14-15]。丁建军等[16]搭建了基于超声波的管道沉降粉尘厚度测量的系统搭建。在一些自然水文和工业生产条件下的颗粒沉积物的超声测量得到越来越多的关注,但缺乏对颗粒沉积动态现象在线监测[17-18]。通过超声数值模拟结合实验测量、浑液面观测、在线取样和图像等手段,搭建高浊度水絮凝沉淀实验系统,对高岭土颗粒絮凝沉淀过程测量和研究,探讨颗粒絮凝沉淀全过程超声监测可行性。
2 理论模型与数值计算 2.1 理论模型超声波在含颗粒的液固两相流中传播时,产生不同程度的声能量衰减。声衰减主要分为3类:吸收衰减、散射衰减、扩散衰减。目前已有一些较成熟的理论模型对声波动进行模拟,其中以Epstein-Carhart-Allegra-Hawley (ECAH)模型应用最为广泛[19]。Epstein和Carhart在超声压缩波传播理论基础上,增加了对热传导效应的考虑。定义并推导出压缩波kc、剪切波ks和热波kT如式(1)所示。
| $\begin{array}{*{20}{l}} {\;\;{k_{\rm{c}}} = \frac{\omega }{c} + i{\alpha _{\rm{L}}}}\\ {\;{k_{\rm{s}}} = (1 + {\rm{i}}){{[\frac{{\omega \rho }}{{2\eta }}]}^{\frac{1}{2}}}}\\ {{k_{\rm{T}}} = (1 + {\rm{i}}){{[\frac{{\omega \rho {c_p}}}{{2k}}]}^{\frac{1}{2}}}} \end{array}$ | (1) |
式中:ω为角频率,rad·s-1;ρ为密度;η为黏度;cp为比定压热容,J·kg-1·K-1;k为热膨胀系数,10-6 K-1;-L为纵波的声衰减系数;i为虚部,各波势函数Y如式(2)给出。
| $Y = \sum\limits_{n = 0}^\infty {{i^n}} (2n + 1){A_n}{H_n}({k_r}){P_n}(\cos \theta )$ | (2) |
式中:An为局部声波振幅,V;Hn(kr)为分散相第一类Bessel函数或者连续相第一类Hankel函数;Pn为Legendre多项式,表征了3种波的角度分布特性;θ为超声散射角。Allegra与Hawley进一步完善了模型适用范围,赋予了液固、气液方程组通解,形成了ECAH模型。原则上,以此为基础,可通过实验声衰减谱,借助反演算法求解颗粒粒度分布和体积分数[20]。就研究的高岭土颗粒而言,考虑到其存在形貌不规则度和团聚效应影响,所以在1 ≤ ωτv≤100时,需用式(3)所示公式[21]进行衰减系数修正。
| $\alpha = {\alpha _0}{(\omega {\tau _\nu })^\gamma }$ | (3) |
| ${\tau _\nu } = \frac{{2{a_{32}}^2{\rho _s}}}{{9{\mu _f}}}$ | (4) |
式(3)中:α为经过修正后的衰减值,NP·m-1;α0为理想球体模拟衰减值,NP·m-1;τv为黏性弛豫时间,s;颗粒半径越小,黏性弛豫时间越短。对普通流体而言,颗粒不规则性的影响在惯性和散射体系中比在黏性体系中更重要。式(4)中:a32为索太尔平均半径,μm;μf为连续相黏度,Pa·s;ρs为分散相密度,kg·m-3。γ取值与形貌及团聚效应有关,与频率无关,参照文献[22]取γ为0.413。
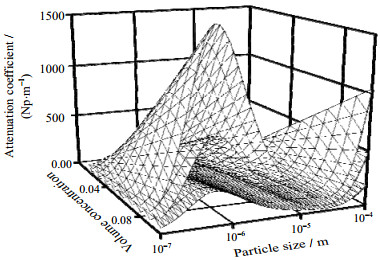
2.2 数值计算与模型敏感性分析表 1为纯水和高岭土物性参数,表中f为超声频率。根据表 1所列物性参数,在频率为2、5、8 MHz,粒度范围为0.1~100 μm,体积分数为0~10% 时,对超声衰减系数进行数值计算。结果如图 1所示,衰减系数随着颗粒粒径增加先后呈两个峰(热黏性吸收峰和衍射峰),随频率和体积分数呈正相关增长趋势,其中,对于微米级颗粒(如1~10 μm),其对浓度改变尤其敏感。
|
|
表 1 纯水和高岭土物性参数(25 ℃) Table 1 Physical parameters of water and kaolin(25 ℃) |
|
图 1 衰减系数数值模拟结果 Fig.1 Numerical simulation results of attenuation coefficients |
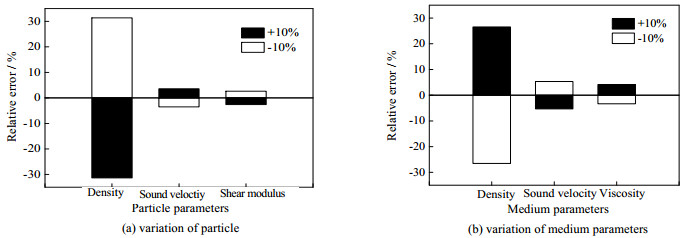
参照表 1数据探究物性参数对衰减的敏感性,对体积分数为5%、超声频率为5 MHz、颗粒直径为2.64 μm高岭土颗粒的水悬浊液,将单一物性参数变化范围±10% 进行计算[23]。
由图 2可见,无论是分散颗粒相还是连续介质相的密度、声速参数对结果影响最大,介质黏度和颗粒剪切模量参数也有一定的影响,其余未列参数(颗粒比热容、剪切模量、纯水导热系数等)对模拟结果影响甚小。
|
图 2 模型参数敏感性 Fig.2 Sensitivity of model parameters |
实验配制悬浊液样品采用麦克林公司产高岭土颗粒,絮凝剂采用鹏捷环保公司产聚合氯化铝(PAC)和聚丙烯酰胺(PAM)。实验用高岭土颗粒和絮凝剂均可溶于水,高岭土样品为白色粉末(密度:2.62 g·cm-3),其颗粒大小为2.64 μm,PAC与PAM的颗粒大小分别为1 303和1 593 μm,其中PAC与PAM质量比为1:590~1:600。
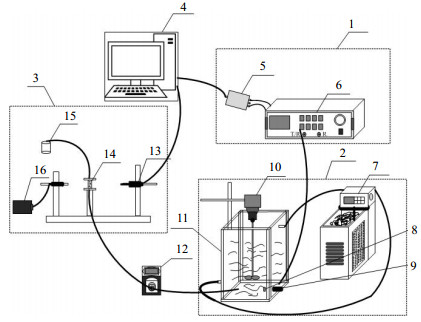
3.2 实验系统和实验过程图 3所示实验系统由3部分组成:浑液面观测、超声测量、图像观测与在线采样系统,可同步实现浑液面观测、超声测量、在线取样与图像测量功能。对比样品池上的对照刻度,可通过肉眼观测浑液面的沉降,并实时记录浑液面水平高度;超声测量装置由5 MHz超声探头(V310-SU)、采集卡(USB-5133)和超声脉冲激励仪(CTS-8077PR)组成,利用底部反射板、减震层和外部固定环实现对水平反射回波信号测量;图像测量与在线取样分析由工业相机、样品池、卤素灯与样品杯组成,图像与在线取样均通过导管将底部(同超声测量区)沉积物抽取后相机拍摄、收集样品后期烘干称重,图像法用以监测不同时间段絮凝沉淀物状态,在线取样获得的浓度参数作为实验参考值;恒温搅拌由针对实验设计的定制有机玻璃装置、恒温水槽(DC-0520ST)和搅拌器构成,通过搅拌使絮凝剂与高岭土颗粒充分接触。本研究为测量高岭土絮凝沉淀过程,考虑到实验中沉淀持续时间较长,容器体积较大,通过对装置外壳增加恒温水循环控温,可使溶液温度保持恒定,排除温度因素对实验结果的影响。
|
图 3 絮凝沉淀过程监测实验系统 Fig.3 Experimental setup for flocculation and precipitation detection 1. ultrasonic excitation unit 2. thermostatic, mixing and precipitation unit 3. image acquirement unit 4. computer 5.DAQ card 6. ultrasonic pulse exciter 7. thermostatic water bath 8. reflector 9. ultrasonic transducer 10. stirrer 11. precipitation device 12. peristaltic pump 13. CCD camera 14. sample pool 15. specimen cup 16. halogen lamp |
实验过程如下:将颗粒直径为2.64 μm的高岭土颗粒分别配制成14.0、19.6、27.4、38.4 g·L-1的初始悬浊液3 L,依次加入质量浓度为:0.2和120.0 mg·L-1、0.28和168.0 mg·L-1、0.4和240.0 mg·L-1、0.55和329.3 mg·L-1 PAM-PAC。搅拌前即定时保存图像和超声信号,悬浊液按300 r·min-1快速搅拌15 s,100 r·min-1慢速搅拌65 s。搅拌结束,悬浊液立即生成浑液,液面下降,记录浑液面高度变化,间隔大致为1 mm;超声探头布置在浑液面之下贴近容器底部(测量区直径为11.5 mm),按15 s间隔实时记录信号;在线取样并相机拍摄,直至25 min结束实验。
图 4给出了27.4 g·L-1初始质量浓度悬浊液不同时间颗粒状态。在沉淀初期有较为明显的气泡,其数量随颗粒体积分数上升和颗粒结合程度增强而迅速下降。沉淀中颗粒连接状态在1.6 min前以独立小团状、链条状并存为主,小尺寸絮团逐渐聚集形成紧密网状结构,再过渡到更为密实的块状。后期受限于絮凝浓度过高导致视野受限,图像观测只能在初期对颗粒有限地识别,辅助观测的作用。

|
图 4 不同时刻颗粒絮凝产物状态图 Fig.4 Profiles of particle flocculation at different times |
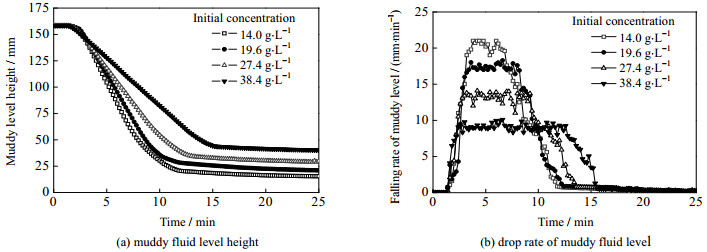
图 5(a)为高岭土颗粒在絮凝沉降过程中浑液面高度随时间变化关系,图 5(b)为浑液面下降速率。结合两图可发现絮凝沉淀中,浑液面下降过程大致可划分为5个速度变化阶段。以初始质量浓度为27.4 g·L-1的高岭土悬浊液为例,第1阶段高岭土絮凝持续时间为0~1.3 min,絮凝剂投入瞬间被水解生成高分子聚合物,水力搅拌促进颗粒快速发生聚集,此时浑液面尚未生成,浑液面高度为悬浊液面初始高度;第2阶段持续时间为1.3~2.4 min,样品经快速和慢速搅拌后絮凝基本完成,形成浑液面并下降,高岭土浑液面高度由158.4降至146.6 mm,浑液面下降速率加快,范围在0~12.2 mm·min-1;第3阶段持续时间为2.4~9.1 min,浑液面持续下降,浑液面下降高度区间最大,由146.6降至61.2 mm,但速率相对稳定,大致在12.2~14.2 mm·min-1;第4阶段持续时间为9.1~13.6 min,浑液面下降速率大幅度减小,由11.9降至0.8 mm·min-1,下降范围由61.2降至33.7 mm;最后阶段,下降速率进一步减小,直到25 min、浑液面高度29.0 mm,过程基本结束。
|
图 5 浑液面高度和下降速率变化 Fig.5 Profiles of muddy liquid level heights and drop rates |
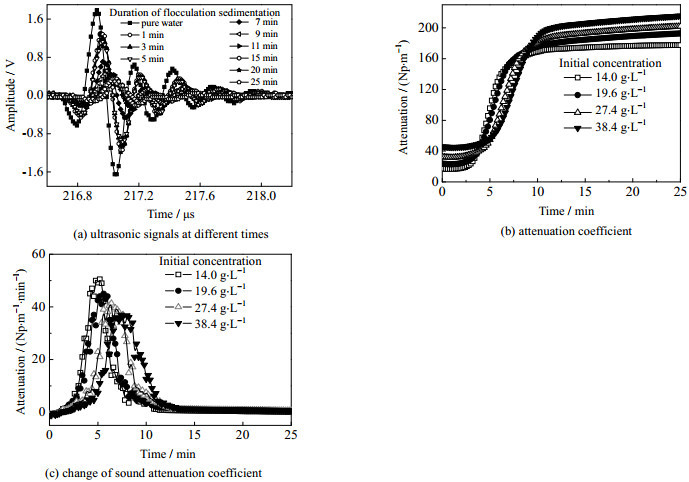
对实验过程超声信号分析,图 6(a)为纯水背景信号和初始质量浓度为27.4 g·L-1悬浊液的高岭土等时长间隔的声波时域信号,可知信号峰值向后退移,在传播距离不变条件下,声时增加、声速减小,变化率为1.8%;同期脉冲信号峰峰值变化率为81.0%,可见幅度变化能更清晰、直观地反映样品声学特性变化。根据峰值计算如图 6(b)、(c)所示的衰减系数、衰减系数变化率。
|
图 6 实验过程声信号变化 Fig.6 Acoustic signal profiles as a function of time during experiments |
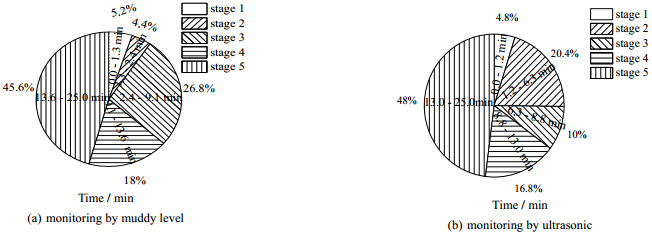
同样以声衰减系数变化对浑液面5个时间阶段分析(初始质量浓度为27.4 g·L-1)。如图 7(a)、(b)所示,浑液面观测法和超声法得到同一絮凝沉淀阶段两者的持续时间相对偏差为:0.4%、16.0%、16.8%、1.2%、2.4%;第1、4、5阶段的起止时刻和持续时间占比均较为接近,但2、3阶段存在较大差距,该种现象产生的主要原因是观测手段不同,超声法测量装置底部絮凝沉积物状态,浑液面观测法则观察整个沉积物的状态。
|
图 7 2种方法观测的时间变化和各阶段分布 Fig.7 Time variation and phase distribution of two methods |
结合图 6和7分析,第1阶段絮凝反应结束,颗粒在无干扰下沉降,孔隙中水分向上顶托产生较大阻力,浑液面得以束缚小颗粒形成整体下沉。第2阶段即浑液面形成初期,属干扰群体沉降,颗粒在重力作用下加速沉降,粗颗粒发生分选下沉,底部浓度快速提升,超声衰减变化率则递增。第3阶段,浑液面过渡到干扰网体沉降,颗粒彼此络合形成网状结构,浑液面下降速率维持相对稳定,底部浓度及声衰减变化率骤减。第4阶段随网体结构紧实,孔隙水被挤压排出,向压缩沉淀过渡,浑液面沉速骤减。形成更均匀分布的伪塑性半固态,上下浓度梯度减小,衰减系数变化率进一步减小。第5阶段全部转换为压缩沉淀,浑液面下降速率维持低值且缓慢递减,体积分数、衰减系数缓慢递增。综上,浑液面内不同阶段的变化反映了颗粒沉降历程和状态变化,而两种方法都揭示了颗粒絮凝沉淀的变化规律。
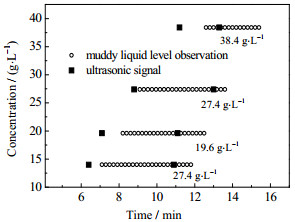
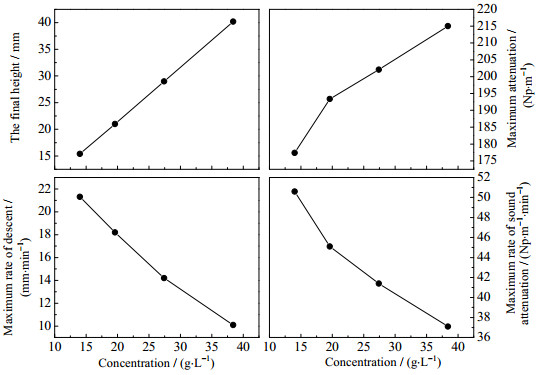
4.3 初始质量浓度影响图 8分析了浑液面下降第4阶段起止时刻与初始质量浓度关系,可以看出,不管是观测法还是超声法,总体反映了相同趋势,即随初始质量浓度增加,其起止时间均向后顺延。图 9给出沉淀过程参数随浓度变化关系,浑液面最终高度(以25 min计)分别为:15.4、21.0、29.0、40.2 mm,与初始浓度呈正相关;最大下降速率则与初始浓度呈负相关。通过声学信号计算,声衰减系数随浓度从177.4增加到215.0 Np·m-1,与初始质量浓度呈正相关,但其最大增长率呈逐减。
|
图 8 第4阶段起止时间与初始质量浓度关系 Fig.8 Relationship between starting/ending times of the fourth stage and initial concentrations |
|
图 9 沉淀过程参数与初始质量浓度关系 Fig.9 Relationship between precipitation parameters |
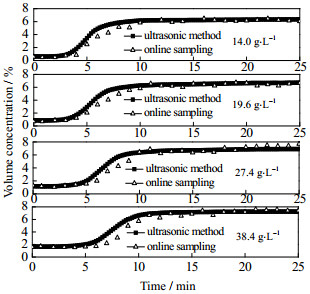
对于已知粒径的颗粒,可由ECAH理论模型结合实验超声衰减信号计算出体积分数。图 10为超声法和在线取样烘干后计算得浑液面底部体积分数变化。由图可知,2种方法给出了类似沉淀过程体积分数变化趋势,该趋势同样反映出沉淀过程特征。在4种初始质量浓度(14.0、19.6、27.4、38.4 g·L-1)下超声法和在线取样法体积分数平均相对误差依次为18.6%、12.1%、11.0%、13.2%,在线取样烘干结果在第5阶段前均略小于超声在线测量结果,这可能与实验过程中取样代表性或扰动带来的误差有关。
|
图 10 超声法和在线取样测量体积浓度 Fig.10 Volume concentrations measured by ultrasonic and online sampling analysis |
作者提出并研究了一种基于脉冲超声波原理,针对高岭土溶液絮凝沉淀过程中浓度高的特性,设计1种非侵入式颗粒絮凝沉淀过程的测量方法。搭建了包含超声测量、浑液面观测、CCD相机拍摄、在线取样功能的实验系统。对4种初始颗粒质量浓度高岭土进行多角度观测和实验。以初始质量浓度为27.4 g·L-1的高岭土为例,以浑液面高度和衰减系数变化,分析沉淀阶段持续时间占比:第1、4、5沉淀阶段的起止和持续时间占比都较为接近(差别0.4%、1.2%、2.4%),2、3阶段存差距;4种初始质量浓度下浑液面最终高度(25 min)范围:15.4 ~ 40.2 mm,对应声衰减系数:177.4~215.0 Np·m-1,均与初始质量浓度呈正相关;基于颗粒不规则程度和聚集效应的修正声波动理论,结合超声实验,分析出浑液面下体积浓度变化,与在线取样法相对误差分别为18.6%、12.1%、11.0%、13.2%。通过关联颗粒絮凝沉淀过程与超声参数,对比浑液面下降速率与超声衰减系数值和变化率,为验证超声测量可行性和对高岭土颗粒絮凝沉淀过程的在线检测提供指导和数据支持。
| [1] |
齐跃明, 杨雅琪, 李鑫, 等. 中美水资源研究现状与发展展望[J]. 西南师范大学学报(自然科学版), 2019, 44(5): 95-102. QI Y M, YANG Y Q, LI X, et al. On status and future prospects of water resources researches in China and U.S[J]. Journal of Southwest China Normal University (Natural Science Edition), 2019, 44(5): 95-102. |
| [2] |
DELELEGN A, WOLDEMARIAM S S, HUSEN A. Water purification and antibacterial efficacy of moringa oleifera lam[J]. Agriculture and Food Security, 2018, 7(1): 25-30. DOI:10.1186/s40066-018-0177-1 |
| [3] |
李海花, 张利辉, 郭茹辉, 等. 阳离子淀粉絮凝剂St-g-PDMC-GTA的合成及其絮凝性能[J]. 高校化学工程学报, 2019, 33(6): 1523-1531. LI H H, ZHANG L H, GUO R H, et al. Synthesis and flocculating properties of cationic starch flocculant St-g-PDMC-GTA[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(6): 1523-1531. |
| [4] |
刘恒, 钟本和, 刘勋, 等. 搅拌槽内絮凝动力学研究[J]. 高校化学工程学报, 2002, 16(4): 378-383. LIU H, ZHONG B H, LIU X, et al. Study of Flocculation Kinetics in a Stirred Tank[J]. Journal of Chemical Engineering of Chinese Universities, 2002, 16(4): 378-383. DOI:10.3321/j.issn:1003-9015.2002.04.005 |
| [5] |
王茜, 朱勇辉, 柴朝晖, 等. 河湖淤泥絮凝沉降特性试验研究[J]. 长江科学院院报, 2020, 37(1): 13-17. WANG Q, ZHU Y H, CHAI C H, et al. Experimental research on flocculation-settling property of silt in rivers and lakes[J]. Journal of Yangtze River Scientific Research Institute, 2020, 37(1): 13-17. |
| [6] |
XU W Y, GAO B Y, YUE Q Y, et al. Effect of preformed and non-preformed Al 13 species on evolution of floc size, strength and fractal nature of humic acid flocs in coagulation process[J]. Separation and Purification Technology, 2011, 78(1): 83-90. DOI:10.1016/j.seppur.2011.01.025 |
| [7] |
王毅, 李平, 罗曼, 等. 磁加载絮凝法处理重金属废水技术的研究进展[J]. 化工进展, 2016, 35(1): 43-51. WANG Y, LI P, LUO M, et al. Research progress on heavy metal wastewater treatment by load magnetic flocculation[J]. Chemical Industry and Engineering Progress, 2016, 35(1): 43-51. |
| [8] |
KADJI C, CANNIE R. ANGELIS D. Prenatal prediction of postnatal large-for-dates neonates using a simplified MRI method: Comparison with conventional 2D ultrasound estimates[J]. Ultrasound in Obstetrics and Gynecology the Official Journal of the International Society of Ultrasound in Obstetrics and Gynecology, 2018, 52(2): 250-257. DOI:10.1002/uog.17523 |
| [9] |
LI X C, ZHAO J M, LIU L, et al. Optical extinction characteristics of three biofuel producing microalgae determined by an improved transmission method[J]. Particuology, 2017, 33(4): 1-10. |
| [10] |
檀奇, 陆亦怀, 陆钒, 等. 基于积分浊度法测量气溶胶散射系数的系统设计与实现[J]. 大气与环境光学学报, 2015, 10(5): 38-45. TAN Q, LU Y H, LU F, et al. Design and implementation of system of measuring aerosol scattering coefficient based on integral turbidity method[J]. Journal of Atmospheric and Environmental Optics, 2015, 10(5): 38-45. |
| [11] |
THI THUY B, DUC CANH N, MOOYOUNG H. Average size and zeta potential of nanobubbles in different reagent solutions[J]. Journal of Nanoparticle Research, 2019, 21(8): 45-49. DOI:10.1007/s11051-019-4618-y |
| [12] |
赵雪莲, 李政, 黄志峰, 等. 微焦点X射线测量微细颗粒沉淀两相流[J]. 清华大学学报(自然科学版), 2005, 45(2): 80-83. ZHAO X L, LI Z, HUANG Z F, et al. Sedimentation measurements of small particle suspensions by a microfocus X-ray tomography system[J]. Journal of Tsinghua University (Science and Technology), 2005, 45(2): 80-83. |
| [13] |
贾楠, 田昌, 苏明旭. 无水醋酸钠结晶过程中析晶温度和颗粒粒径在线测量[J]. 化工学报, 2019, 70(12): 4664-4672. JIA N, TIAN C, SU M X. In situ measurement of crystallization temperature and particle size distribution during crystallization of sodium acetate[J]. CIESC Journal, 2019, 70(12): 4664-4672. |
| [14] |
李运思, 苏明旭, 杨荟楠, 等. 混合弹性颗粒体系声衰减数值模拟[J]. 声学学报, 2017, 42(5): 586-592. LI Y S, SU M X, YANG H N, et al. Simulation of ultrasonic attenuation in the elastic mixing particle system[J]. Chinese Journal of Acoustics, 2017, 42(5): 586-592. |
| [15] |
WANG X, SU M X, Cai X S. Effects of material viscosity on particle sizing by ultrasonic attenuation spectroscopy[J]. Procedia Engineering, 2015, 102: 256-264. DOI:10.1016/j.proeng.2015.01.141 |
| [16] |
丁建军, 陈文刚, 章盛. 基于超声波的管道沉降粉尘厚度的测量系统[J]. 自动化技术与应用, 2017, 36(5): 63-70. DING J J, CHEN W G, ZHANG S. Measurement system for dust deposition thickness of pipeline based on ultrasonic wave[J]. Techniques of Automation and Applications, 2017, 36(5): 63-70. |
| [17] |
SHUKLA A, PRAKASH A, ROHANI S. Particles settling studies using ultrasonic techniques[J]. Powder Technology, 2007, 177(2): 102-111. DOI:10.1016/j.powtec.2007.02.003 |
| [18] |
BAMBERGER J A, GREENWOOD M S. Using ultrasonic attenuation to monitor slurry mixing in real time[J]. Ultrasonics, 2004, 42(1/2/3/4/5/6/7/8/9): 145-148. |
| [19] |
潘晗, 王培红. 基于ECAH模型反演的气固两相流固相浓度测量方法[J]. 热能动力工程, 2018, 33(2): 33-38. PAN H, WANG P H. Method for measuring the solid-phase concentration of a gas-solid two-phase flow based on an inversion model[J]. Journal of Engineering for Thermal Energy and Power, 2018, 33(2): 33-38. |
| [20] |
ZHOU W, SU M X, CHAI X S. Advances in nanoparticle sizing in suspensions: Dynamic light scattering and ultrasonic attenuation spectroscopy[J]. Powder and particle, 2017, 34(1): 168-182. |
| [21] |
EVANS J M. Coupled phase theory for sound propagation in emulsions[J]. Journal of the Acoustical Society of America, 1997, 102(1): 278-282. DOI:10.1121/1.419745 |
| [22] |
HE G C, MAO Y P, NI W. A new fractal modification of ultrasonic attenuation model for measuring particle size in mineral slurries[J]. International Journal of Mineral Processing, 2007, 82(3): 119-125, 169-173. DOI:10.1016/j.minpro.2006.09.005 |
| [23] |
LUM A F H, BORDEN M A, DAYTON P A, et al. Ultrasound radiation force enables targeted deposition of model drug carriers loaded on microbubbles[J]. Journal of Controlled Release, 2006, 111(1/2): 128-134. |




