2. 兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070
2. School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China
中压绝缘件主要采用环氧树脂自动压力凝胶工艺过程(automatic pressure gelation process, APG)制造,被广泛应用于电气开关、控制装置等各种电气设备和系统上,质量控制对绝缘件制品高效生产和可靠应用有重要意义[1-3]。作为典型间歇过程,APG具有高度复杂性和非线性,且产品型号种类繁多、市场需求多变,需满足柔性制造要求,给中压绝缘件质量控制效率提升带来严峻挑战。
中压绝缘件制品质量受到诸多生产工艺参数影响,质量控制常通过APG工艺参数优化实现[4]。工业上常用的试凑法、实验设计法存在严重依赖操作经验、实验成本高、产品质量难以保证最优等问题[5-6]。基于模型的优化方法(model-based optimization, MBO)依赖于高可靠性质量模型,建模成本高且存在模型失配[7-8]。Kong等[6, 9-11]针对以注塑成型为代表的快速、低成本间歇过程质量控制,提出以少量迭代直接实验代替MBO中基于模型质量评价的无模型优化思路(model-free optimization,MFO),在避免高成本建模过程的同时引入高效优化框架,实现质量控制效率提升。为进一步降低MFO质量控制成本,Zhao等[12]提出一种迭代建模与信赖域优化相结合的方法(iterative modeling and trust-region optimization method,IMTO),Lu等[13]提出一种基于自然梯度的无模型方法,均取得一些改进效果。然而,中压绝缘件制造过程虽具有与注塑成型过程类似批次特性,但单批次实验成本更高。因此,仍需进一步提高质量控制效率。
考虑当前新兴数据驱动控制发展趋势,Hou等[14-15]引入数据驱动优化思想提高了无模型控制效率,Xing等[16]在求解复杂优化问题时尝试从优化过程中挖掘待求解问题知识以指导优化过程,Bonvin等[17]指出在一个过程中所收集的数据实际上构成了“最佳模型”,这些研究工作均强调了数据、优化过程知识在控制优化过程中的作用。Kong等[18]在MFO基础上提出利用质量控制过程中所产生优化迭代过程知识信息,指引优化进程的知识指引型优化思路,设计一种基于历史梯度逼近值的改进型并行摄动随机逼近方法(simultaneous perturbation stochastic approximation, SPSA)。本文在知识指引型优化思想基础上,结合优化进程特征,进一步深入挖掘SPSA在优化过程中所产生的历史迭代点信息,提出利用相邻迭代点历史信息对优化进程状态进行动态近似估计,实现优化迭代步长自适应调整的改进型SPSA策略。
2 中压绝缘件制品质量控制在制造材料与APG设备等确定的情况下,中压绝缘件制品质量主要由APG工艺参数决定。因此,中压绝缘件制品质量控制可等价为APG生产工艺参数优化整定问题。
在不考虑工业现场噪声的情况下,可将制品质量与工艺参数间数学关系表示为
| $Q = f\left( {\mathit{\boldsymbol{X}}} \right){, _{}}{\mathit{\boldsymbol{X}}} = {\left[ {{x_{1}}, {x_{2}}, \; \cdots \;, \;{x_{n}}} \right]^{\rm{T}}}$ | (1) |
式中:Q为制品质量;X为工艺参数向量,维度为n;xi为第i个工艺参数分量,i=1, 2,
设Qt为待控制质量目标,可将中压绝缘件制品质量控制问题定义如下:
| $\begin{gathered} \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{X}}} \;{Q_{\rm{E}}} = \left| {f({\mathit{\boldsymbol{X}}}) -{Q_{\rm{t}}}} \right| \\ {\rm{s}}{\rm{.t}}{\rm{.}} \\ {\mathit{\boldsymbol{R}}}_i^{\rm{L}} \leqslant {x_{^i}} \leqslant {\mathit{\boldsymbol{R}}}_i^{\rm{H}}, i = 1, 2, \cdots , n; \\ \end{gathered} $ | (2) |
式中:QE为绝缘件制品质量偏差,RiH和RiL分别为第i个工艺参数分量上下限。
优化命题(2)本质上为带边界约束非线性优化问题。鉴于APG过程质量模型难以获得,而过程具有批次可重复性特征,为减少质量模型建模成本,实现中压绝缘件质量在线、实时控制,可采用不基于质量模型的无模型优化作为上述优化问题的解决方案。在无模型优化架构下,绝缘件质量控制可通过工艺参数在线调整、实验、质量检测与反馈等一系列环节按批次迭代实现。
3 基于相邻迭代点信息的知识指引型SPSA方法 3.1 知识指引型优化策略优化方法性能决定质量控制效率,是绝缘件质量控制关键。传统无模型优化方法具有较高优化效率,能满足快速、低成本间歇过程质量控制需要。然而APG过程批次实验成本较高,对实验迭代批次数敏感,因此在中压绝缘件质量控制问题上,该方法仍面临实验成本相对高的问题。
在无模型质量控制架构下,优化搜索过程会动态产生一系列历史迭代过程信息。这些信息事实上都蕴含一定过程知识。在传统无模型方法中,这类信息并未被充分利用。以基于SPSA的无模型优化方法为例,它在每次迭代点搜索时均仅依赖于当前迭代点及其相应摄动点信息,而未考虑其他优化过程历史信息。而如果能够利用质量控制优化过程所产生的历史迭代点信息去充分挖掘过程对象特征和监测质量控制进程状态,那么就能对质量控制进程干预和调节,从而提高优化效率,降低质量控制成本。这种对传统无模型质量控制方法进行改进,融合过程知识信息以指引优化进程的策略,称为知识指引型质量优化策略(knowledge-informed quality optimization,KQO)[18]。总体架构如图 1所示。本节从知识指引型优化策略思想出发,探讨SPSA方法在相邻迭代点知识信息融合下的改进策略及其实现机制。

|
图 1 基于知识指引型质量优化策略的中压绝缘件质量控制总体架构 Fig.1 Framework of knowledge-informed quality optimization for quality control of medium voltage insulator |
SPSA是一种随机梯度逼近优化方法[19],它在每个迭代点处并行摄动所有分量以产生正、负2个摄动点,再利用摄动点损失函数值估计当前迭代点近似梯度。相比有限差分随机逼近方法(finite difference stochastic approximation, FDSA),梯度估计成本显著下降,因此具有较高优化效率[20-21],适合于在无模型质量控制框架下应用。SPSA方法主要流程如下:
1) 方法初始化:确定待优化工艺参数及其可行域,根据经验或特定法则选取初始点X1,并设置适当优化方法系数及迭代终止条件。
2) 优化步长调整:迭代更新当前批次优化步长ak、ck。其中,迭代步长ak计算式如下:
| ${a_k} = \frac{a}{{{{(A + k + 1)}^\alpha }}}$ | (3) |
式中:a、A、α为方法系数,k为当前迭代批次数,ak为在第k批次下迭代步长。ak为迭代批次数k的函数,由式(3)可知它随迭代优化进程推进而单调下降。
摄动步长计算式如下:
| ${c_k} = \frac{c}{{{{(k + 1)}^\gamma }}}$ | (4) |
式中:c、γ为方法系数,ck为在第k批次迭代下摄动步长。
3) 摄动点产生:通过蒙特卡洛方式生成n维摄动向量Δk,其每一维均由伯努利±1分布随机产生,向量内每个分量都互相独立且满足零均值原则。设当前迭代点为Xk,产生的正向摄动点为:Xk+ ckΔk,负向摄动点为:Xk-ckΔk。
4) 损失函数值评价:分别获取第k批次下迭代点及正、负向摄动点的损失函数值L(Xk)和L(Xk±ckΔk)。
5) 梯度估计:按下式利用正、负向摄动点及其相应损失函数值计算当前迭代点处近似梯度值。
| $G\left( {{\mathit{\boldsymbol{X}}}{}_k} \right) = \frac{{L\left( {{\mathit{\boldsymbol{X}}}{}_k + {c_k}{{\mathit{\boldsymbol{\boldsymbol{\varDelta} }}}_k}} \right) -L\left( {{\mathit{\boldsymbol{X}}}{}_k -{c_k}{{\mathit{\boldsymbol{\boldsymbol{\varDelta} }}}_k}} \right)}}{{\left( {{\mathit{\boldsymbol{X}}}{}_k + {c_k}{{\mathit{\boldsymbol{\boldsymbol{\varDelta} }}}_k}} \right) -\left( {{\mathit{\boldsymbol{X}}}{}_k -{c_k}{{\mathit{\boldsymbol{\boldsymbol{\varDelta} }}}_k}} \right)}}$ | (5) |
6) 迭代点更新:根据下式搜索确定下一迭代点:
| ${{\mathit{\boldsymbol{X}}}_{k + 1}} = {{\mathit{\boldsymbol{X}}}_k} -{a_k}G({{\mathit{\boldsymbol{X}}}_k})$ | (6) |
7) 终止条件判断:判断是否满足优化终止准则。若满足,停止迭代,输出最优工艺参数设定值;若不满足,返回第2步,继续迭代。
3.3 基于相邻迭代点历史信息的改进型SPSA优化思路传统SPSA方法虽然已具较高优化效率,但也存在若干潜在缺陷。首先,其迭代步长调整机制相对固化,是一单调减函数,随优化进程推进而不断减小。迭代步长单调下降意义在于有助于确保方法收敛性,但也因此造成步长不具备对优化进程状态的适应性和方法缺乏自适应优化搜索能力。例如,在方法运行初始阶段,即使所搜索方向并非良好改进方向,但根据该机制都会获得较大迭代步长,可能造成优化进程初始振荡;同时,随着迭代次数增加,迭代步长持续减小,此时即使优化进程探测到良好改进方向,但受限于过小步长而被限制在该方向上的搜索幅度,造成优化效率低下。因此,相对固化的步长机制在一定程度上限制了SPSA优化效率提升。其次,SPSA仅利用当前迭代点处有限信息,简单、易于实施,但也意味着它丧失了对优化进程的全局感知能力。最后,在上述因素共同制约下,SPSA易于陷入局部极小,复杂场景下会严重影响控制优化效果。
为提高绝缘件质量控制效率,在无模型优化架构下,可采取两项措施:1)改变SPSA迭代步长的固化调整机制,给迭代步长调整引入动态自适应能力,2)利用历史迭代点信息获得优化进程状态感知能力。式(6)中,引入动态补偿因子实现迭代步长动态调整;优化进程状态可依赖历史迭代点信息进行感知和识别,并作为优化策略动态调整的依据。
为实现上述优化改进,对工业问题(不失一般性,以最小化问题为例)的一般优化进程特征进行分析。如图 2所示为典型优化轨迹整体形态示意图。根据优化进程在局部小邻域内发展趋势和形态,优化轨迹所含局部优化场景可划分为2种类型:局部单调下降场景和局部振荡场景。其中,根据单调下降速率及趋势,又可将局部单调下降场景划分为局部快速下降场景与局部减速下降场景(介于2种场景间为临界状态)。局部振荡场景可根据其形态不同划分为局部凹型振荡场景与局部凸型振荡场景。在局部邻域内可根据若干相邻历史迭代点的相对关系来近似判别当前优化进程所处场景,并据此指引优化进程。

|
图 2 典型优化轨迹整体形态示意图 Fig.2 Schematic diagram of the overall shape of a typical optimization trajectory |
考虑迭代点信息的局部有效性和相对置信度,以选取含当前迭代点在内的相邻3组批次迭代点信息为宜。根据相邻3组迭代点信息来划分的4种局部优化场景形态示意图如图 3所示。

|
图 3 典型局部优化场景形态示意图 Fig.3 Schematic diagram of typical local optimization scenarios |
当系统优化进程处于局部快速下降场景时,按当前优化轨迹趋势,能够有较大预期目标函数值仍将随迭代进程推进而获得显著改进,此时可适度加大迭代步长;而在局部减速下降场景及2类局部振荡场景时,有较大预期优化进程正逼近某局部极小,考虑优化进程收敛性,应适度减小迭代步长。因此,迭代过程中若能利用相邻迭代点信息实现SPSA方法对当前优化状态的准确判定,则可据此相应调整迭代步长,从而在确保收敛性的条件下加速优化进程。为实现对4种局部场景的简易判别,可利用当前相邻3组迭代点损失函数信息。首先,构造相邻迭代点损失函数信息集Lkajt (k≥3):{L(Xk-2), L(Xk-1), L(Xk)}。构造判别因子如下:
| ${\mathit{\Lambda} _k} = L\left( {{{\mathit{\boldsymbol{X}}}_k}} \right) -L\left( {{{\mathit{\boldsymbol{X}}}_{k -1}}} \right)$ | (7) |
| ${\mathit{\Lambda} _{k -1}} = L\left( {{{\mathit{\boldsymbol{X}}}_{k -1}}} \right) -L\left( {{{\mathit{\boldsymbol{X}}}_{k -2}}} \right)$ | (8) |
| ${\mathit{\Lambda} _{k\Gamma }} = {\mathit{\Lambda} _k} -\delta {\mathit{\Lambda} _{k -1}} = L\left( {{{\mathit{\boldsymbol{X}}}_k}} \right) + \delta L\left( {{{\mathit{\boldsymbol{X}}}_{k -{\rm{2}}}}} \right) -\left( {{\rm{1}} + \delta } \right)L\left( {{{\mathit{\boldsymbol{X}}}_{k -{\rm{1}}}}} \right)$ | (9) |
式中:相对改进因子Λk为Xk和Xk-1两迭代点损失函数值之差,Λk-1为Xk-1和Xk-2两迭代点损失函数值之差;加权因子ΛkΓ表征相邻3个迭代点损失函数值间的复合关系;δ为临界调节系数。
当局部优化轨迹位于下降阶段时,若ΛkΓ < 0,轨迹处于局部快速下降场景;若ΛkΓ > 0,轨迹处于局部减速下降场景;若ΛkΓ=0,轨迹处于临界状态。3种状态的相对关系如图 4所示。综上,考虑各优化场景特性,以式(7)~(9) 3因子为基础可得局部优化邻域优化状态简易判别准则,如表 1所示。

|
图 4 局部下降场景的划分 Fig.4 Divisions of local descending scenarios |
|
|
表 1 局部邻域优化状态划分及简易判别准则 Table 1 Status scenarios and discrimination rules for local optimization |
通过表 1简易准则,可近似判别不同优化场景。在局部快速下降场景,应适度增大步长;在局部下降临界状态下,步长不变;在其他场景下,应适度减小步长。步长调整幅度可依赖于相邻迭代点间距离关系。基于该思路,本文提出一种利用优化过程相邻迭代点知识信息以指引优化进程的改进型SPSA方法。该方法利用相邻连续3次迭代点信息来识别当前优化进程状态,据以实现迭代步长动态自适应调整,从而提高优化效率。该方法被称为基于相邻迭代点历史信息的知识指引型SPSA(Knowledge-informed SPSA based on adjacent iteration points information, IK-SPSA),是一种典型知识指引型优化策略。
3.4 改进型SPSA方法实现机制IK-SPSA继承传统SPSA基本流程,核心区别在于它融合了优化过程中相邻迭代点信息,在这些历史迭代信息指引下实现了迭代步长动态自适应调整。改进前、后方法流程图如图 5所示。其中,图 5(a)为传统SPSA流程。图 5(b)为改进型IK-SPSA方法流程,相比传统SPSA方法,它增加了步长动态调整环节。

|
图 5 SPSA与IK-SPSA的流程图 Fig.5 Flowcharts of SPSA and IK-SPSA |
在IK-SPSA方法基础上,本文构造了一种可行改进策略。在该策略下,迭代步长调整机制设计如下:
| ${d_k} = {a_k}\left( {1 + \xi {\psi _k}\Delta {d_k}} \right)$ | (10) |
式中:dk为调整后的当前迭代步长;ak为根据SPSA原迭代步长计算机制(式(3))所得当前初始迭代步长;
| ${\psi _k} = {\psi _k}\left( {L_k^{\rm{ajt}}} \right) = {\operatorname{sgn} _{}}\left( {{\mathit{\Lambda} _{k\Gamma }} \cdot {\mathit{\Lambda} _{k -1}}} \right)$ | (11) |
式中:sgn (·)为符号函数。
迭代步长调整因子Δdk由相邻迭代点参数集Xkajt按下式确定:
| $\Delta {d_k} = \Delta {d_k}\left( {{\mathit{\boldsymbol{X}}}_k^{\rm{ajt}}} \right) = \frac{{|{{\mathit{\boldsymbol{X}}}_k} -{{\mathit{\boldsymbol{X}}}_{k -1}}|}}{{|{{\mathit{\boldsymbol{X}}}_{k -1}} -{{\mathit{\boldsymbol{X}}}_{k -2}}|}}$ | (12) |
式中:Xkajt={Xk-2, Xk-1, Xk}, k≥3,为连续3次迭代点工艺参数信息的集合;∣Xk-Xk-1∣、∣Xk-1-Xk-2∣分别为迭代点k与k-1、k-1与k-2间欧式距离。
引入基于相邻迭代点信息的知识指引机制后,迭代点更新策略调整为
| ${{\mathit{\boldsymbol{X}}}_{k + 1}} = {{\mathit{\boldsymbol{X}}}_k} -{d_k}G({{\mathit{\boldsymbol{X}}}_k})$ | (13) |
本文以某类型支柱绝缘子作为实验对象,制造材料为环氧树脂,型号为Duresco Nu 5680V。考虑重量是该类绝缘子的一项重要质量指标,因此以绝缘子重量作为被控质量指标。绝缘子重量设定值需根据产品规格确定,以保证性能符合产品规范要求。在验证过程中,分别选用A和B两种不同型号绝缘子作为实验对象,其中A型绝缘子重量设定值为635 g,B型绝缘子620 g。根据工艺控制要求,合格绝缘子重量偏差容限为0.5 g。鉴于熔体温度、注射时间、保压时间和保压压力等4种工艺参数对绝缘子重量影响最为显著,实验中选择这4种工艺参数作为待优化工艺参数X=[x1, x2, x3, x4]T。上述工艺参数的表征及取值范围如表 2所示。
|
|
表 2 缘子重量控制的主要工艺参数 Table 2 Process parameters for weight control of post insulators |
在无模型质量控制架构下,优化过程需迭代试验并测量不同工艺参数组合下的制品重量。考虑到方法验证过程需要一定数量筛选实验,而绝缘件制品实验成本相对高昂,为提高验证效率,本文采用以代理模型为基础的中压绝缘件仿真模型来代替实际绝缘件制造过程。鉴于本文着重于绝缘件质量控制方法研究,采用具有足够精度的代理模型并不会影响质量控制方法验证的有效性。
建立中压绝缘件重量代理模型的过程如下:首先根据实际绝缘件型号参数和规格要求,基于Solidworks建立绝缘子3D仿真模型,如图 6所示;在此基础上,利用成型模拟软件Moldflow建立绝缘子机理模型;然后,在Moldflow模型基础上利用拉丁方格设计(Latin hypercube sampling, LHS)进行实验设计,通过一系列仿真实验对绝缘子重量与工艺参数间联系进行观测;再利用仿真实验数据,基于BP神经网络(back-propagation artificial neural network,BPANN)建立绝缘子重量代理模型。图 7(a)为绝缘件重量BPANN神经网络拓扑图,图 7(b)为基于BPANN的重量代理模型在测试样本上的预测性能。该模型最大误差为1.5%,显示其具有较高拟合精度,能满足质量控制验证要求。

|
图 6 支柱绝缘子3D模型 Fig.6 3D model of the post insulator |

|
图 7 基于BPANN的支柱绝缘子重量模型及其预测性能 Fig.7 BPANN-based weight model of the post insulator and its prediction performance |
为验证IK-SPSA有效性,对IK-SPSA和传统SPSA在不同初始点下的重量控制性能进行比较研究。测试中选择A型支柱绝缘子,其重量控制目标为635 g,容许重量偏差为0.5 g。为保证性能比较的合理性及有效性,2种方法除迭代步长调整机制不同外,其他条件(包括所有方法系数)均保持一致。为保证优化初始点的随机性和代表性,本文采用拉丁方格设计选取若干组不同初始点;再从这些不同初始点出发分别利用IK-SPSA和SPSA实现支柱绝缘子重量控制。
随机选取某一次重量控制过程为例,IK-SPSA和SPSA均从同一初始点X1=[151.16, 0.34, 5.9, 82.65]T出发对绝缘子进行重量控制。初始点重量为659.9 g,其重量控制动态过程如图 8所示。在此次实验中,IK-SPSA仅用22次迭代达到重量控制目标,而SPSA则需要26次迭代。从图 8(a)中可明显看出,在此次重量控制过程中,IK-SPSA表现优于SPSA。图 8(b)显示了2种方法的迭代步长轨迹,可清楚看到SPSA方法下迭代步长随迭代次数增加单调下降,步长变化相对固化;而IK-SPSA的迭代步长在优化进程相邻迭代点信息基础上实现了动态调节,使得IK-SPSA能更快速趋近控制目标。同时,也应注意到迭代步长动态调整幅度随优化进程推进呈下降趋势,该特性可确保改进机制不影响方法总体收敛性。

|
图 8 初始点X1=[151.16, 0.34, 5.9, 82.65]T下IK-SPSA与SPSA重量控制轨迹 Fig.8 Trajectories of IK-SPSA and SPSA on weight control with initial point X1=[151.16, 0.34, 5.9, 82.65]T |
为进一步验证IK-SPSA有效性,再选取另一个初始点X1=[225.92, 0.35, 5.81, 80.79]T下重量控制实验结果进行展示。2种方法都在相同条件下进行测试。此时初始重量为612.3 g,重量控制轨迹如图 9(a)所示。本次实验中,IK-SPSA通过15次迭代快速达到目标,SPSA则需要27次迭代,重量控制速率明显慢于IK-SPSA。图 9(b)为2种方法下迭代步长变化轨迹,图中轨迹同样体现了IK-SPSA迭代步长动态调整机制的作用。为观察IK-SPSA方法在控制参数上的并行摄动特征,将本次重量控制实验下工艺参数的变动轨迹绘制如图 10所示。图中各工艺参数均按其可行域进行标度化,范围为0~100%。从图中可看出,随着重量控制进程推进,优化进程中所有迭代点工艺参数均随迭代批次同步改变,最终趋向于最优工艺参数。

|
图 9 初始点X1=[225.92, 0.35, 5.81, 80.79]T下IK-SPSA与SPSA重量控制轨迹 Fig.9 Trajectories of IK-SPSA and SPSA on weight control with initial point X1=[225.92, 0.35, 5.81, 80.79]T |

|
图 10 IK-SPSA控制参数的变动轨迹 Fig.10 Trajectories of the process parameters of IK-SPSA with X1=[225.92, 0.35, 5.81, 80.79]T |
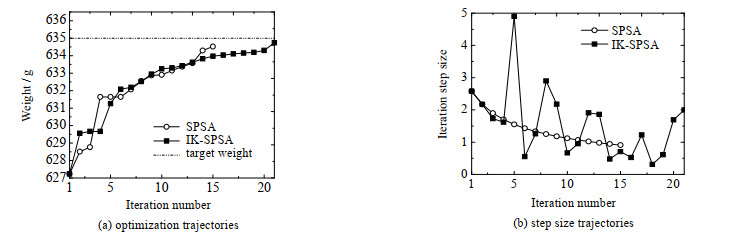
尽管IK-SPSA具有良好的优化特性,但它并不能保证每次搜索都优于SPSA。无论IK-SPSA还是SPSA都属于随机逼近方法,方法本身带有天然的随机性,因而其优化轨迹在每次运行时都不相同。在筛选实验测试结果中,可观察到部分测试下SPSA表现优于IK-SPSA的情况。如图 11所示为一组IK-SPSA重量控制速率慢于SPSA的情况。需要说明的是,这种现象的出现是符合预期的,事实上,它充分体现了这类方法的随机性特征,与2种方法的相对控制性能比较并无冲突。
|
图 11 初始点X1=[212.35, 0.42, 7.4, 83.1]T下IK-SPSA与SPSA重量控制轨迹 Fig.11 Trajectories of the process parameters of IK-SPSA with X1=[212.35, 0.42, 7.4, 83.1]T |
由于随机逼近方法的随机性,IK-SPSA方法相对SPSA方法的效率应通过统计分析来评价。为最大程度覆盖工艺参数优化区间,尽量消除统计结果不确定性,实验设计采用基于多批次拉丁方设计的实验方案。首先将各工艺参数可行域进行N等分,采用传统拉丁方设计生成N个随机采样点,分别从生成采样点出发测试SPSA与IK-SPSA的重量控制性能,记录其各自迭代次数(即质量控制成本)。然后,批次重复拉丁方设计(M组)。随批次数增加,随机实验样本数累加,持续观测IK-SPSA相对SPSA在迭代次数上的累积平均下降率。通过IK-SPSA在累积平均下降率上的变化趋势和近似收敛数值实现对2种方法的相对性能评估。如图 12(a)所示即为100组(M=100)批次拉丁方设计(N=10)的累积平均下降率变化轨迹。由图可见,当批次较少时,迭代次数累积平均下降率会随批次变化而发生较大波动。这客观上表明,少量批次拉丁方设计下,因样本数有限,平均下降率并不能准确、稳定反映IK-SPSA与SPSA的相对性能差异。而随着拉丁方设计批次数增加,累积平均下降率将渐趋稳定。本实验中,下降率由最初32.2%逐渐下降至11%左右,并最终趋向稳定在11.4%。该数值较准确地反映IK-SPSA相对SPSA的性能改进幅度。如图 12(b)所示为M×N (1 000)次测试中IK-SPSA相对SPSA方法的相对性能统计。在所有1 000次测试中,IK-SPSA在476组中表现更好,即迭代次数更少,占比47.6%;IK-SPSA与SPSA迭代次数相同为262组,占比26.2%;而IK-SPSA劣于SPSA,为262组,占比26.2%。从统计结果看,与SPSA相比,IK-SPSA在支柱绝缘子重量控制上,性能有显著提升。

|
图 12 IK-SPSA相对效率统计结果 Fig.12 Statistical results of relative efficiency of IK-SPSA |
IK-SPSA作为一种随机逼近方法,在本质上具有随机性。为进一步验证方法在重量控制上的可重复性,将该方法在同一初始点上进行重复测试。不失一般性,随机选取初始点X1=[242.49, 0.34, 8.34, 89.5]T。如图 13所示为IK-SPSA从该初始点出发下的3次不同重量控制轨迹。由图可见,每次重量控制测试下优化轨迹均不相同,轨迹不重叠。但每次测试,IK-SPSA都能在有限迭代批次下快速到达重量控制目标。实验结果显示,3次重量控制分别需要23、20、28次迭代。鉴于IK-SPSA的随机性,这种现象是合理的。该测试显示,IK-SPSA虽然在从同一初始点出发的多个不同重量控制轨迹上不具备控制轨迹的重复性,但具备在控制性能上的可重复性。

|
图 13 从随机初始点X1=[242.49, 0.34, 8.34, 89.5]T出发3次不同优化批次可重复性测试 Fig.13 Repeatability results with three different optimization runs from a random selected initial point X1=[242.49, 0.34, 8.34, 89.5]T |
由于市场需求多变,支柱绝缘子制造过程产品规格也常随之发生快速变化。为应对产品规格快速变化下产品型号切换的需要,质量控制方法必须具备良好的目标跟踪能力。为验证IK-SPSA在型号切换情况下对质量目标跟踪的快速性和有效性,实验中对绝缘子重量跟踪性能进行了测试。假定当前产品线生产A型绝缘子,其重量目标设定值为635 g。选取初始点X1=[160.87, 0.26, 3.68, 83.22]T,初始重量为617.3 g。如图 14所示为重量跟踪测试结果。实验结果显示在第一阶段重量控制下2种方法均能快速达到目标重量,其中IK-SPSA使用7次迭代,而SPSA需要14次。假定在某稳态时刻,需要切换生产目标重量为620 g的B型绝缘子。此时进入轨迹第二阶段,当前工艺参数下重量输出偏离B型绝缘子重量目标。在型号切换过程中,IK-SPSA仅用7次迭代即达到新的重量控制目标;SPSA则需要12次迭代,显示2种方法均能快速达到新的重量设定值,从而满足产品生产型号快速切换要求。结果表明,IK-SPSA同SPSA方法一样,对重量目标跟踪是有效的。

|
图 14 型号切换下重量跟踪性能测试轨迹 Fig.14 Trajectories of weight target tracking under type transition |
在工业环境中,绝缘子制造过程容易受到各种干扰。当过程受到扰动时,质量控制稳定状态可能被破坏。此时,控制方法需要对工艺参数进行调整,将质量回复到原设定值。为验证IK-SPSA方法在扰动下质量控制的鲁棒性,实验中以环氧树脂材料配方变化引起的产品重量波动作为干扰信号,测试方法在扰动发生后的重量控制性能。测试中选用A型绝缘子,目标重量为635 g,扰动发生前系统在重量控制下已达到重量目标并保持稳定状态。假设某时刻,材料配方发生变化,并且假定该变化将引起绝缘子重量发生6 g偏差(实验中为模拟环氧树脂材料配方变化而引起的产品重量波动,人为引入一恒定重量干扰信号)。当偏差发生后,在原工艺条件下,绝缘子重量输出将偏离设定值。型号A产品重量控制的过程及发生扰动时利用IK-SPSA回复原重量目标的整个过程如图 15所示。由图所示,当干扰发生后,重量输出产生了明显偏差。此时,IK-SPSA被激活。随后在IK-SPSA作用下,产品重量经过17次迭代再次回复到设定重量控制目标。结果表明,IK-SPSA在质量控制上具有较好鲁棒性,能够有效应对外部扰动。

|
图 15 扰动下的重量控制轨迹 Fig.15 Trajectories of weight control under disturbance |
本文对利用优化迭代过程中的迭代点信息以指引优化搜索进程的知识指引型优化思想进行了进一步探索和扩展,为解决具有较高批次成本的中压绝缘件质量控制问题提供了一种可行思路。在知识指引型优化思想基础上,本文结合优化进程特征和SPSA特性,利用相邻迭代点历史信息对优化进程状态加以动态识别,构建了一种基于相邻迭代点信息的迭代步长动态调节机制,形成一种新型SPSA改进方法。该方法在某支柱绝缘子重量控制问题上进行仿真验证。验证结果表明该方法有效,且相对传统SPSA方法具有更高优化效率,可有效降低中压绝缘件质量控制成本。本文所提出的知识指引型优化策略可进一步扩展到其他方法及其他间歇过程质量控制问题。
| [1] |
ZHANG Q, LI J H, HAN X T, et al. Partial discharge characteristics of cavities with different appearances and positions in solid insulation[J]. IEEE Electrical Insulation Magazine, 2019, 35(4): 34-40. DOI:10.1109/MEI.2019.8735668 |
| [2] |
范建平. 环氧树脂压力凝胶的自动注料系统[J]. 江苏电器, 2001(4): 36-38. FAN J P. Automatic material feeding system for epoxy resin pressure gel[J]. Jiangsu Dianqi, 2001(4): 36-38. |
| [3] |
吴建红, 葛乐矣, 王福润, 等. 中压固体绝缘环氧树脂APG制造新工艺[J]. 电工电气, 2015(1): 47-50. WU J H, GE L Y, WANG F R, et al. Medium-voltage solid insulation epoxy APG manufacturing new technology[J]. Electrotechnics Electric, 2015(1): 47-50. DOI:10.3969/j.issn.1007-3175.2015.01.013 |
| [4] |
李志勇. APG压注工艺在中压互感器制造中的应用[J]. 变压器, 2015, 52(7): 32-35. LI Z Y. Application of automatic pressure gelation (APG) technology on manufacture of MV instrument transformer[J]. Transformer, 2015, 52(7): 32-35. |
| [5] |
胡可可, 刘旭平, 蔡海波, 等. 基于Box-Behnken实验设计与响应面法优化禽流感疫苗生产工艺[J]. 高校化学工程学报, 2019, 33(2): 394-399. HU K K, LIU X P, CAI H B, et al. Optimization of avian influenza vaccine culturing by Box-Behnken design and response surface methodology[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(2): 394-399. DOI:10.3969/j.issn.1003-9015.2019.02.018 |
| [6] |
孔祥松.快速、低成本间歇过程无模型优化方法研究[D].杭州: 浙江大学, 2011. KONG X S. Model-free optimization for a type of batch processes with a short cycle time and low operational cost[D]. Hangzhou: Zhejiang University, 2011. |
| [7] |
王普, 曹彩霞, 高学金, 等. 基于扩展得分矩阵的多阶段间歇过程质量预测[J]. 高校化学工程学报, 2019, 33(3): 664-671. WANG P, CAO C X, GAO X J, et al. Quality prediction of multistage batch processes based on extended score matrices[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(3): 664-671. DOI:10.3969/j.issn.1003-9015.2019.03.021 |
| [8] |
华丰, 田亮, 邱彤. 基于递归神经网络的化工反应过程建模[J]. 高校化学工程学报, 2019, 33(5): 1186-1194. HUA F, TIAN L, QIU T. Modeling of chemical reaction processes based on recurrent neural networks[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(5): 1186-1194. DOI:10.3969/j.issn.1003-9015.2019.05.021 |
| [9] |
KONG X S, YANG Y, CHEN X, et al. Quality control via model-free optimization for a type of batch process with a short cycle time and low operational cost[J]. Industrial & Engineering Chemistry Research, 2011, 50(5): 2994-3003. |
| [10] |
ZHU S Q, YANG Y, YANG B, et al. Model-free quality optimization strategy for a batch process with short cycle time and low operational cost[J]. Industrial & Engineering Chemistry Research, 2014, 53(42): 16384-16396. |
| [11] |
YANG Y, YANG B, ZHU S Q, et al. Online quality optimization of the injection molding process via digital image processing and model-free optimization[J]. Journal of Materials Processing Technology, 2015, 226: 85-98. DOI:10.1016/j.jmatprotec.2015.07.001 |
| [12] |
ZHAO J J, YANG Y, CHEN X, et al. An iterative modeling and trust-region optimization method for batch processes[J]. Industrial & Engineering Chemistry Research, 2015, 54(12): 3186-3199. |
| [13] |
LU N Y, ZHAO F. Quality control of batch process using natural gradient based model-free optimization[J]. IFAC Proceedings Volumes, 2014, 47(3): 8335-8340. DOI:10.3182/20140824-6-ZA-1003.01000 |
| [14] |
HOU Z S, WANG Z. From model-based control to data-driven control: survey, classification and perspective[J]. Information Sciences, 2013, 235: 3-35. DOI:10.1016/j.ins.2012.07.014 |
| [15] |
LEI T, HOU Z S, REN Y. Data-driven model free adaptive perimeter control for multi-region urban traffic networks with route choice[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(7): 2894-2905. DOI:10.1109/TITS.2019.2921381 |
| [16] |
邢立宁, 陈英武. 基于知识的智能优化引导方法研究进展[J]. 自动化学报, 2011, 37(11): 1285-1289. XING L N, CHEN Y W. Research progress of knowledge-based intelligent optimization guidance methods[J]. Acta Automatica Sinica, 2011, 37(11): 1285-1289. |
| [17] |
BONVIN D, GEORGAKIS C, PANTELIDES C C, et al. Linking models and experiments[J]. Industrial & Engineering Chemistry Research, 2016, 55(25): 6891-6903. |
| [18] |
KONG X S, GUO J M, ZHENG D B, et al. Quality control for medium voltage insulator via a knowledge-informed SPSA based on historical gradient approximations[J]. Processes, 2020, 8(2): 146. DOI:10.3390/pr8020146 |
| [19] |
SPALL J C. Introduction to stochastic search and optimization: estimation, simulation, and control [M]. New Jersey: John Wiley & Sons, Inc, 2003.
|
| [20] |
SPALL J C. An overview of the simultaneous perturbation method for efficient optimization[J]. Johns Hopkins APL Technical Digest, 1998, 19(4): 482-492. |
| [21] |
SPALL J C. Implementation of the simultaneous perturbation algorithm for stochastic optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(3): 817-823. DOI:10.1109/7.705889 |




