2. 浙江省蓄能与建筑节能技术重点实验室,浙江 杭州 310030;
3. 中国石油大学(北京) 化学工程与环境学院,北京 昌平 102249
2. Key Laboratory of Energy Storage and Building Energy-Saving Technology of Zhejiang Province, Hangzhou 310030, China;
3. School of Chemical Engineering and Environment, China University of Petroleum, Beijing 102249, China
在我国工业领域中,常有大量低温余热资源没有得到回收利用。目前对低温余热的定义不尽相同[1-3],一般可认为200 ℃以下的余热为低温余热。在我国石化行业中,低温余热的占比可达80%[3]。由于温度等级低,回收利用技术难度高,低温余热的浪费情况非常严重。据估计,我国北方每年损失近7.6×1014 J,约合2.6亿吨标准煤当量(tce)的低温余热[4]。与此同时,大量化石燃料燃烧产生高品质能源,以满足城市建筑物的能源需求。如果能在城市供热供冷中有效地利用工业低温余热,则可以减少化石燃料的消耗和温室气体的排放量,并提高能源的利用效率[5]。当前已有一些研究致力于将低温余热整合到区域供暖系统中,例如,Fang等[2]提出一种估算低温余热利用潜力的方法,Tveit等[6]为一座造纸厂与市政能源系统的整合设计换热网络。
在传统的建筑物制冷方式中,独立的小型制冷机用于满足每个房间或建筑物的冷量需求,如家用空调。近年来,利用大型制冷站集中制冷并将冷量输送至周边用户的区域供冷技术得到了重视和发展。Söderman[7]提出一种包括冷却设备在内的区域供冷优化模型。中央冷却设备的制冷方式可分为压缩式制冷和吸收式制冷2种,相比于主要由电驱动的压缩式制冷,吸收式制冷能够利用低温余热资源来驱动制冷循环的运转[3, 8],从而提高能源的利用效率,这使得吸收式制冷技术在区域供冷中具有较强的吸引力。相比于直接利用低温余热进行区域供暖,将低温余热用于制冷供冷的研究较少,而且很少有研究能在考虑用户需求随季节波动的基础上给出各周期下具体的操作方案。
本研究旨在通过回收工业低温余热来提供驱动吸收式制冷机所需的热量,从而满足用户的冷量需求。本文的主要工作是建立相关数学模型,以制冷的年成本最小化为目标函数,运用数学规划法确定在已知冷量需求下的余热回收方案。建筑物对冷量的需求往往随季节变化,因此在模型中加入了多周期的描述,并考虑了不同周期下的系统操作优化。
2 问题表述对于某些类型的建筑物,例如医院,往往一年四季都有冷量需求,被称为冷阱。将每个季节视为一个周期,周期的集合记为S = {T}。假设冷阱各周期的冷量需求量Qcd(T)已知,在离冷阱合适的距离范围内有一工厂,冷阱需要的冷量由该工厂提供。工厂内部有若干条余热流股i,集合为I = {i},其入口温度θhin(i)、目标温度θhout(i)、热容流率Fh(i)、热负荷Qh(i)均已知。在不与制冷系统进行整合的情况下,这些热量由循环冷却水直接排放到环境中。通过以工艺软水为介质与这些余热流股换热,可以得到较高温度的热水,用以驱动LiBr吸收式制冷机组的运转。完成制冷后,热水的温度降低。由于在工厂内部各余热流股与制冷机组间的距离往往不可忽略而且并不相等,因此需要用泵将热水输送至各余热流股的换热器,从而完成循环。在整个过程中,工厂的年费用(total annual cost,TAC)可由式(1)表示。
| ${\rm{TAC}} = {C_{{\rm{exchanger}}}} + {C_{{\rm{pump, cap}}}} + {C_{{\rm{pump, op}}}} + {C_{{\rm{cu}}}} + {C_{{\rm{machine, cap}}}} + {C_{{\rm{machine, op}}}}$ | (1) |
式中:Cexhanger为换热器的年成本,Cpump, cap为泵的设备年成本,Cpump, op为泵的操作费用,Ccu为冷公用工程费用,Cmachine, cap为LiBr机组的设备年成本,Cmachine, op为LiBr机组的操作费用。其中,Ccu和Cmachine, op分别为
| ${C_{{\rm{cu}}}} = {u_{{\rm{ccu}}}} \cdot {Q_{{\rm{cu, h}}}}$ | (2) |
| ${C_{{\rm{machine, op}}}} = {u_{{\rm{ccu}}}} \cdot {Q_{{\rm{cu, m}}}} + {C_{\rm{e}}}$ | (3) |
式中:uccu为冷公用工程的单位费用,Qcu, h为余热流股仍需要的冷公用工程用量,Qcu, m为制冷机组需要的冷却负荷,Ce为制冷机组的电能费用。由于制冷机组消耗的电能与输入的热能相比可以忽略不计[9],因此本文忽略制冷机组的电能费用,Cmachine, op的计算可简化为
| ${C_{{\rm{machine, op}}}} = {u_{\rm{c}}}_{{\rm{cu}}} \cdot {Q_{{\rm{cu, m}}}}$ | (4) |
Qcu, h和Qcu, m分别为
| ${Q_{{\rm{cu, h}}}} = {Q_{{\rm{h0}}}} - {Q_{\rm{r}}}$ | (5) |
| ${Q_{{\rm{cu, m}}}} = {Q_{\rm{r}}} + {Q_{{\rm{cold}}}}$ | (6) |
式中:Qh0为所有余热流股原本需要的冷却负荷,Qr为回收得到的用于制冷的热量,Qcold为LiBr机组的制冷量。故余热流股和制冷机组需要的总冷却公用工程负荷Qcu, total为
| ${Q_{{\rm{cu, total}}}} = {Q_{{\rm{cu, h}}}} + {Q_{{\rm{cu, m}}}} = ({Q_{{\rm{h0}}}} - {Q_{\rm{r}}}) + ({Q_{\rm{r}}} + {Q_{{\rm{cold}}}}) = {Q_{{\rm{h0}}}} + {Q_{{\rm{cold}}}}$ | (7) |
由此可见,Qcu, total可视为定值,则Ccu与Cmachine, op之和为定值。另外,LiBr机组的设备费用与制冷容量有关,在制冷负荷已知的情况下,Cmachine, cap也为可以确定的值。因此,为简化求解,目标函数中可去除无优化空间的Ccu、Cmachine, op和Cmachine, cap三项。故使得工厂年费用最小的目标函数为
| ${\rm{min}} \left\{ {{\rm{TAC'}} = {C_{{\rm{exchanger}}}} + {C_{{\rm{pump, cap}}}} + {C_{{\rm{pump, op}}}}} \right\}$ | (8) |
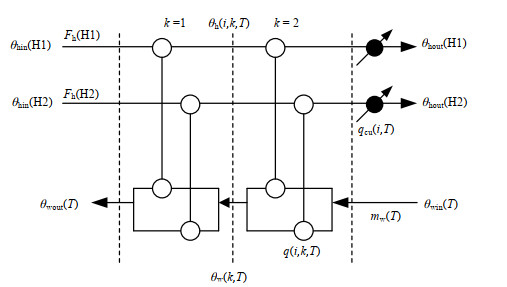
为实现热量的梯级回收,采用分级换热网络超结构[10]描述余热回收。由于冷阱的供冷负荷随季节变化,因此有关变量需要引入周期集合S来表示,如图 1所示。图中,θh(i, k, T)为周期T下热物流i在k温区的热端温度,θwin(T)为周期T下热水进行换热的入口温度,θwout(T)为周期T下热水进行换热的出口温度,θw(k, T)为周期T下热水在k温区的热端温度,mw(T)为周期T下热水的质量流率,q(i, k, T)为周期T下热水在温区k从热物流i回收的热量,qcu(i, T)为周期T下热物流i需要的冷公用工程负荷。热水和余热流股需要满足进出口温度约束。
| ${\theta _{\rm{h}}}(i, 1, T) = {\theta _{{\rm{hin}}}}(i)$ | (9) |
| ${\theta _{\rm{w}}}(1, T) = {\theta _{{\rm{wout}}}}(T)$ | (10) |
| $ {\theta _{\rm{w}}}(NT + 1, T) = {\theta _{{\rm{win}}}}(T) $ | (11) |
|
图 1 分级超结构示意图 Fig.1 The stage-wise superstructure |
式中:θh(i, 1, T)为周期T下热物流i在第一个温区热端的温度,θw(1, T)为周期T下热水在第一个温区热端的温度,θw(NT+1, T)为周期T下热水在最后一个温区冷端的温度。
在一些设定的条件下(溶液浓度、溶液热交换器效率等),驱动LiBr制冷机组循环的热水进出口温度有较明显的线性关系[9],对文献[9]中的数据进行线性拟合可得到
| ${\theta _{{\rm{win}}}}(T) = 0.426 \cdot {\theta _{{\rm{wout}}}}(T) + 52.8$ | (12) |
热水和余热流股满足热量平衡方程(13)~(15)。
| ${F_{\rm{h}}}(i) \cdot \left[ {{\theta _{{\rm{hin}}}}\left( i \right) - {\theta _{{\rm{hout}}}}\left( i \right)} \right] = \sum\limits_{k \in st} {q\left( {i, k, T} \right)} + {q_{{\rm{cu}}}}(i, T)$ | (13) |
| ${F_{\rm{h}}}(i) \cdot \left[ {{\theta _{\rm{h}}}(i, k, T) - {\theta _{\rm{h}}}(i, k + 1, T)} \right] = q(i, k, T)$ | (14) |
| ${c_{{\rm{pw}}}} \cdot {m_{\rm{w}}}(T) \cdot \left[ {{\theta _{\rm{w}}}(k, T) - {\theta _{\rm{w}}}(k + 1, T)} \right] = \sum\limits_{i \in I} {q(i, k, T)} $ | (15) |
式中:θh(i, k+1, T)为周期T下热物流i在k温区的冷端温度,θw(k+1, T)为周期T下热水在k温区的冷端温度,cpw为水的比热容。
换热器的存在与否可以由热负荷逻辑约束和传热温差逻辑约束来确定。
| $q(i, k, T) \leqslant {z_{\rm{T}}}(i, k, T) \cdot {Q_{\rm{h}}}(i)$ | (16) |
| ${\rm{\Delta }}\theta (i, k, T) \leqslant {\theta _{\rm{h}}}(i, k, T) - {\theta _{\rm{w}}}(k, T) + \left[ {1 - {z_{\rm{T}}}(i, k, T)} \right] \cdot {\rm{\Delta }}{\theta _{\max }}$ | (17) |
| ${\rm{\Delta }}\theta (i, k + 1, T) \leqslant {\theta _{\rm{h}}}(i, k + 1, T) - {\theta _{\rm{w}}}(k + 1, T) + \left[ {{\rm{1}} - {z_{\rm{T}}}(i, k, T)} \right] \cdot {\rm{\Delta }}{\theta _{\max }}$ | (18) |
| $\Delta \theta (i, k, T) \geqslant \Delta {\theta _{\min }}$ | (19) |
式中:zT(i, k, T)为决定周期T下热水在温区k与热物流i之间的换热器是否存在的二元变量,Δθ(i, k, T)和Δθ(i, k+1, T)分别为该换热器热端和冷端的传热温差。Δθmax为传热温差上限,取250 ℃。Δθmin为最小传热温差,取Δθmin= 10 ℃。
周期T下热物流i的冷却器的负荷为
| ${q_{{\rm{cu}}}}(i, T) = {F_{\rm{h}}}(i) \cdot \left[ {{\theta _{\rm{h}}}(i, NT + 1, T) - {\theta _{{\rm{hout}}}}(i)} \right]$ | (20) |
式中:θh(i, NT+1, T)为周期T下热物流i在最后一个温区的冷端温度。
对于热水在温区k与热物流i之间的换热器来说,若至少有一个周期下该换热器存在,则该换热器就应存在。该关系的表达式为
| $z(i, k) \geqslant {z_{\rm{T}}}(i, k, T)$ | (21) |
式中:z(i, k)为确定热水在温区k与热物流i之间的换热器是否存在的二元变量。
周期T下热水在温区k回收热物流i的热量所需要的换热面积AeT(i, k, T)由式(22)计算。
| ${A_{{\rm{eT}}}}(i, k, T){\rm{ = }}q(i, k, T) \cdot \left[ {{h_{\rm{w}}}^{ - {\rm{1}}} + {h_{\rm{h}}}{{(i)}^{ - {\rm{1}}}}} \right]/{\theta _{{\rm{LMTD}}}}(i, k, T)$ | (22) |
式中:hw为热水的传热系数,hh(i)为热物流i的传热系数,θLMTD(i, k, T)为该换热器的对数平均传热温差,为降低求解难度,其计算在此采用Chen近似式[11]:
| ${\theta _{{\rm{LMTD}}}}(i, k, T) = {\left\{ {\Delta \theta (i, k, T) \cdot \Delta \theta (i, k + 1, T) \cdot \left[ {\Delta \theta (i, k, T) + \Delta \theta (i, k + 1, T)} \right]/{\rm{2}}} \right\}^{{\rm{1/3}}}}$ | (23) |
对于多周期换热网络,换热器面积Ae(i, k)应取各周期下面积的最大值[12],这里采用不等式约束来表示,其上限值将由目标函数来限制。
| ${A_{\rm{e}}}(i, k) \geqslant {A_{{\rm{eT}}}}(i, k, T)$ | (24) |
对于LiBr单效制冷机,在可以忽略机组消耗的电能的情况下[9],各周期下制冷负荷与输入的热量之间的关系为
| ${Q_{{\rm{cd}}}}(T) = {\rm{CO}}{{\rm{P}}_{}}(T) \cdot \left\{ {{c_{{\rm{pw}}}} \cdot {m_{\rm{w}}}(T) \cdot \left[ {{\theta _{{\rm{wout}}}}(T) - {\theta _{{\rm{win}}}}(T)} \right]} \right\}$ | (25) |
式中:COP(T)为周期T下制冷机的性能系数(coefficient of performance),它与进入制冷机的热水温度(即θwout(T))有关。在制得的冷媒水温度为7 ℃的情况下,不同的θwout(T)所对应的COP(T)由文献[9]提供。COP(T)与θwout(T)并非呈线性关系,因此为降低求解难度,不能直接对两者进行线性拟合,而应进行分段线性拟合,结果如式(26)所示。值得说明的是,在不同的冷媒水温度下,COP(T)与θwout(T)有着不同的对应关系,冷媒水温度可以作为优化变量。但目前将其作为变量纳入模型中会造成求解困难,因此在本文中,冷媒水温度设为定值7 ℃。
| ${\rm{COP}}(T) = \left\{ {\begin{array}{*{20}{c}} {0.0437 \cdot {\theta _{{\rm{wout}}}}(T) - 4.217, 100 \leqslant {\theta _{{\rm{wout}}}}(T) \leqslant 110} \\ {0.0082 \cdot {\theta _{{\rm{wout}}}}(T) - 0.312, 110 \leqslant {\theta _{{\rm{wout}}}}(T) \leqslant 120} \\ {0.0043 \cdot {\theta _{{\rm{wout}}}}(T) - 0.156 , 120 \leqslant {\theta _{{\rm{wout}}}}(T) \leqslant 130} \\ {0.0018 \cdot {\theta _{{\rm{wout}}}}(T) - 0.488, 130 \leqslant {\theta _{{\rm{wout}}}}(T) \leqslant 150} \end{array}} \right.$ | (26) |
如果热水在第k个温区分流成多股与多条余热流股进行换热,则在稳定流动的状态下每条热水支路的压降均相等。然而,各余热流股i到制冷机组的距离不相等,使得单独输送时距离造成的压头损失Hf, branch(i)不相等,因此第k温区的总压头损失Hf, total(k, T)应为各支路的Hf, branch(i)的最大值,这里采用不等式约束来表示,其上限值将由目标函数来限制,如式(27)所示。
| ${H_{{\rm{f, total}}}}(k, T) \geqslant {z_{\rm{T}}}(i, k, T) \cdot {H_{{\rm{f, branch}}}}(i)$ | (27) |
对于Hf, branch(i)较小的支路,为保证该支路的热水流量不发生改变,应通过阀门增加额外的压头损失Hf, valve(i, k, T),从而使该支路的压头损失等于Hf, total(k, T)。
| ${H_{{\rm{f, valve}}}}(i, k, T) = {H_{{\rm{f, total}}}}(k, T) - {H_{{\rm{f, branch}}}}(i)$ | (28) |
简化后的工厂年费用TAC’中只包括Cexchanger、Cpump, cap和Cpump, op三项,计算公式为
| ${C_{{\rm{exhanger}}}} = {\rm{AF}} \cdot \left\{ {\alpha \cdot \sum\limits_{i \in I} {\sum\limits_{k \in st} {z(i, k) + } } \beta \cdot {{\sum\limits_{i \in I} {\sum\limits_{k \in st} {\left[ {{A_{\rm{e}}}(i, k)} \right]} } }^\gamma }} \right\}$ | (29) |
| ${C_{{\rm{pump, cap}}}} = {\rm{AF}} \cdot \left( {a + b \cdot {P_{{\rm{rated}}}}^c} \right)$ | (30) |
| ${P_{{\rm{rated}}}} \geqslant \frac{{{m_{\rm{w}}}(T) \cdot g \cdot \sum\limits_{k \in st} {{H_{{\rm{f, total}}}}(k, T)} }}{{\eta \cdot {1_{}}000}}$ | (31) |
| $ {C}_{\rm{pump, op}}={u}_{\rm{c}}{}_{\rm{e}}\cdot {\displaystyle \sum _{T\in S}\frac{{m}_{\rm{w}}(T)\cdot g\cdot {\displaystyle \sum _{k\in st}{H}_{\rm{f, total}}(k, T)}}{\eta \cdot {1}_{}000}}\cdot t(T)$ | (32) |
式中:AF为年金因子(annualized factor),α、β、γ为换热器设备成本参数,a、b、c为泵的设备成本参数,g为重力加速度,η为泵的效率,uce为单位电价,Prated为泵的额定功率,t(T)为各周期的时间。
4 案例研究与结果分析 4.1 案例数据基于上述混合整数非线性规划(MINLP)模型,进行一项案例研究。工厂的余热流股的有关数据见表 1,其中各流股的输送压头Hf, branch(i)作为参数直接给出,仅用来表示余热流股与制冷机组的距离远近。各周期的时间和各周期下医院的冷量需求量见表 2。
|
|
表 1 余热流股数据 Table 1 The data of hot streams |
|
|
表 2 制冷量数据表 Table 2 The data of cooling demand |
各方程中涉及的有关参数取值如下[13]:cpw= 4.2 kJ·kg-1·℃-1,hw = 1.8 kW·m-2·℃-1,hh(i)= 2.0 kW·m-2·℃-1,g = 9.81 N·kg-1,AF= 0.264,α= 11 000 $,β= 150 $·m-2,γ= 1,a = 8 600 $,b = 7 310 $·kW-1,c = 0.2,uce = 0.1 $·(kW·h)-1,η = 0.7。
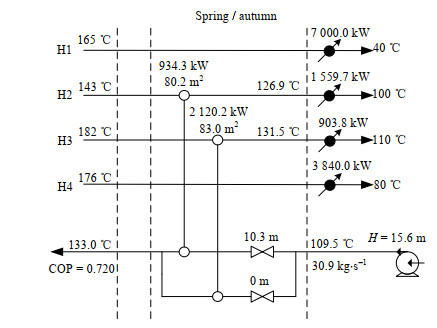
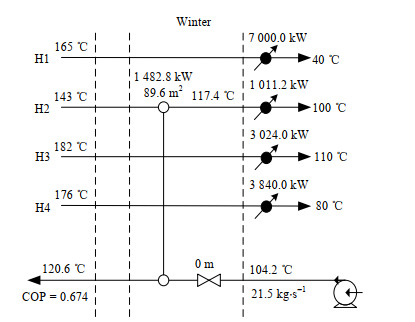
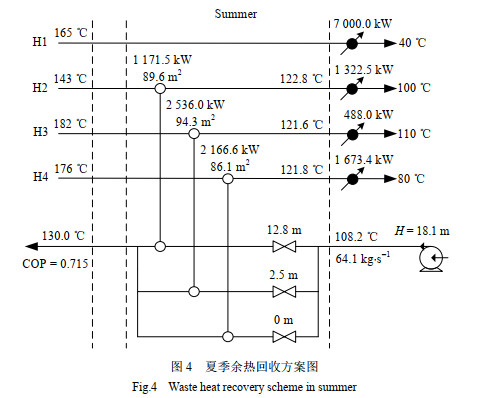
4.2 结果与讨论本研究使用的求解工具为GAMS软件的DICOPT求解器,得到的各周期下的余热回收方案如图 2~4所示,TAC’和各项费用见表 3。
|
图 2 春/秋季余热回收方案图 Fig.2 Waste heat recovery scheme in spring/autumn |
|
图 3 冬季余热回收方案图 Fig.3 Waste heat recovery scheme in winter |
|
图 4 夏季余热回收方案图 Fig.4 Waste heat recovery scheme in summer |
|
|
表 3 经济性数据表 Table 3 The economic data |
从Cexchanger、Cpump, cap和Cpump, op三项的计算方程中可以看出,影响TAC’大小的核心变量是热水的出口温度θwout(T)。当θwout(T)增大时,LiBr机组的COP值升高,需要回收的热量减小,且热水进出口温差增大,因此热水的质量流量降低,泵的费用减小。但与此同时换热器的传热温差减小,会导致所需要的换热面积增大,使换热器设备费用增大。反之,当θwout(T)减小时,泵的费用增大,换热器的费用减小。因此目标函数求解的核心就是换热器费用与泵费用之间的权衡。得到的结果表明,为使得TAC’值最小,θwout(T)应处于120 ~ 135 ℃。
由于各周期下医院的冷量需求差异明显,工厂的余热回收方案也随之发生变化。随着制冷量的减小,需要参与热量回收的余热流股数减少,未用于制冷的余热流股仍由原先设置的冷却器进行冷却。流股H1的温位虽然不低,但其热量在4个周期下均未得到回收,这是因为H1距离制冷机组较远,若将热水输送至H1处则需要泵提供较高的压头,使得泵的费用增大,因此在其他3条流股的热量能够满足制冷需求的情况下,完全可以不用回收H1的热量。由此可见,本案例中余热量大于制冷所需的热量,若制冷所需的热量增大,则可能会出现H1的余热也被利用的情况。在制冷量最小的冬季,热水出口温度降低至120.6 ℃时,仅与距离制冷机组最近的H2流股换热即可满足制冷机组热量需求,此时距离较远的流股H3和H4的换热器可以关停。这说明余热流股与制冷机组之间的距离对余热回收方案有着不可忽视的影响,应优先选择回收距制冷机组较近的余热流股的热量。
在制冷量最大的夏季,换热器需要提供较大的换热面积。在这种情况下,春季和秋季的热水可以取较高的出口温度,不仅使换热器面积的使用率较高,还能减小热水的质量流率,从而降低泵的费用。而在冬季,如果选择只回收流股H2的热量,则热水的出口温度不能取太高,这是因为传热温差的限制,当θwout(T)增大时,H2流股可以提供的热量会减小,直至热量的需求无法得到满足,从而要求再回收另一条流股的热量,造成泵的费用增大。因此,应在保证能用最少的流股满足热量需求的前提下提高θwout(T),否则会使TAC’增大。
由于承担了医院的供冷任务,工厂需要增加制冷机组、换热器和泵的成本。但与此同时,出售冷量可以为工厂带来收入。可以求得工厂供冷的总投资TAC为769 564 $。取供冷单价为120 $·(MW·h)-1,则供冷收入为2 589 120 $,大于TAC。由此可见,回收工业低温余热用于吸收式制冷,不仅可以实现能量的有效利用,还能为工厂带来可观的经济收益。
5 结论本研究建立了工业余热用于区域供冷的多周期优化方法。通过对MINLP模型的求解,可以得到各周期下的余热回收方案。结果表明,核心优化变量是得到的热水温度θwout(T),它导致了泵的费用和换热器费用之间的权衡。当θwout(T)增大时,泵的费用降低,换热器费用增大。在研究的案例中,各周期下θwout(T)的取值均在120 ~ 135 ℃。在不同周期中,由于制冷量的变化,参与热量回收的工业流股数也会相应变化,冬季制冷量最小,因此只有一条工业余热物流参与余热制冷,其他余热物流由循环水系统冷却,反之夏季制冷量最大,则参与余热制冷的物流最多。在满足热量需求的前提下,热水应优先回收距制冷机组较近的余热流股的热量,从而减少泵的费用,使工厂的年费用TAC’最小。该方法可以优化出系统的最优设计和每个季节下系统的具体操作,经济性评估的结果表明,本案例中回收工业低温余热用于吸收式制冷的总成本为769 564 $,远小于收入2 589 120 $,经济效益显著。
| [1] |
JI C Z, QIN Z, DUBEY S, et al. Three-dimensional transient numerical study on latent heat thermal storage for waste heat recovery from a low temperature gas flow[J]. Applied Energy, 2017, 205: 1-12. DOI:10.1016/j.apenergy.2017.07.101 |
| [2] |
FANG H, XIA J J, ZHU K, et al. Industrial waste heat utilization for low temperature district heating[J]. Energy Policy, 2013, 62: 236-246. DOI:10.1016/j.enpol.2013.06.104 |
| [3] |
连红奎, 李艳, 束光阳子, 等. 我国工业余热回收利用技术综述[J]. 节能技术, 2011, 29(2): 123-133. LIAN H K, LI Y, SHU G Y Z, et al. An overview of domestic technologies for waste heat utilization[J]. Energy Conservation Technology, 2011, 29(2): 123-133. DOI:10.3969/j.issn.1002-6339.2011.02.006 |
| [4] |
FANG H, XIA J J, JIANG Y. Key issues and solutions in a district heating system using low-grade industrial waste heat[J]. Energy, 2015, 86: 589-602. DOI:10.1016/j.energy.2015.04.052 |
| [5] |
LI Y, REZGUI Y, ZHU H X. District heating and cooling optimization and enhancement-Towards integration of renewables, storage and smart grid[J]. Renewable and Sustainable Energy Reviews, 2017, 72: 281-294. DOI:10.1016/j.rser.2017.01.061 |
| [6] |
TVEIT T M, AALTOLA J, LAUKKANEN T, et al. A framework for local and regional energy system integration between industry and municipalities-Case study UPM-Kymmene Kaukas[J]. Energy, 2006, 31(12): 2162-2175. DOI:10.1016/j.energy.2005.09.009 |
| [7] |
SӦDERMAN J. Optimisation of structure and operation of district cooling networks in urban regions[J]. Applied Thermal Engineering, 2007, 27(16): 2665-2676. DOI:10.1016/j.applthermaleng.2007.05.004 |
| [8] |
XIA L, LIU R M, ZENG Y T, et al. A review of low-temperature heat recovery technologies for industry processes[J]. Chinese Journal of Chemical Engineering, 2018, 27(10): 2227-2237. |
| [9] |
王晨升.采用过程余热提供冷量的匹配研究[D].北京: 中国石油大学(北京), 2016. WANG C S. Match between process waste heat and cold capacity supplied by absorption refrigeration[D]. Beijing: China University of Petroleum, 2016. |
| [10] |
YEE T F, GROSSMANN I E. Simultaneous optimization models for heat integration Ⅱ: Heat exchanger network synthesis[J]. Computers & Chemical Engineering, 1990, 14(10): 1165-1184. |
| [11] |
CHEN J J J. Letter to the editors: Comments on improvement on a replacement for the logarithmic mean[J]. Chemical Engineering Science, 1987, 42(10): 2488-2489. DOI:10.1016/0009-2509(87)80128-8 |
| [12] |
VERHEYEN W, ZHANG N. Design of flexible heat exchanger network for multi-period operation[J]. Chemical Engineering Science, 2006, 61(23): 7730-7753. DOI:10.1016/j.ces.2006.08.043 |
| [13] |
CHANG C L, CHEN X L, WANG Y F, et al. An efficient optimization algorithm for waste Heat Integration using a heat recovery loop between two plants[J]. Applied Thermal Engineering, 2016, 105: 799-806. DOI:10.1016/j.applthermaleng.2016.04.079 |




