1 引言

塔式太阳能热发电系统通过大规模定日镜场反射汇聚太阳光到位于塔顶的接收器上，加热传热介质从而带动后续发电过程。传热介质的蓄热能力能够有效地弥补太阳光的波动性和间歇性，有利于太阳能电站的并网发电和大规模利用；此外，采用高塔中心集热方式，塔式太阳能热电站能够获得较高的介质温度和较高的发电效率，因此，塔式太阳能热发电被认为是最有前景的太阳能热利用方式^[1]。

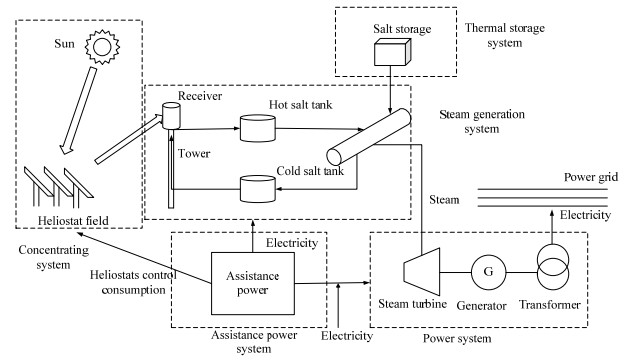
图 1为塔式太阳能热发电系统示意图，其中，由定日镜场(heliostat field)和接收器组成的聚光集热系统的建造成本占总成本比例高，镜场的光学效率和接收器的传热效率基本决定了整个系统的发电效率^[2]。然而，在电站运行中，由于太阳光的发散性、镜面误差以及跟踪误差等原因，定日镜反射成像光斑较大，当接收器面积一定时，会导致部分能量在接收器外即溢出损失，降低电站的发电效率。为解决该问题，国内外都有相关研究从定日镜场和接收器的优化设计2个方面进行。

定日镜的优化方面，合理地选择子镜的安装角度能够在不增加额外成本的情况下减小定日镜溢出损失。已投入运行的塔式太阳能热电站大多采用多个子镜来拼接成大面积定日镜，如美国的Solar One和西班牙的PS10等^[3-4]，但都采用简单的平面拼接方式。国内外学者提出倾斜安装子镜的方法来提高定日镜的聚光性能，主要包括静态和动态倾斜2种方法^[5]。动态倾斜方式给各子镜安装独立的转向驱动机构，实时调节子镜角度，但这种方式安装和运行成本太大，目前只在仿真比较中使用。静态倾斜方法对各子镜采取固定的倾斜角度，主要有同轴式(on axis)、离轴式(off axis)和抛物面式3种^[5-6]。同轴式倾斜安装各定日镜子镜时，各子镜法向量和中心子镜向量于2倍焦距处相交，这种倾斜方式参照了碟式太阳能集热器，对于塔式太阳能热定日镜与接收器位置各异及入射光线角度实时变化的情形，效果欠佳。离轴式倾斜策略针对不同时刻子镜最优倾斜角度不同的情况，选取某一时刻的最优角度(该时刻称为倾斜时刻)，固定下来运用于全年。Jones^[7]比较了Solar Two的lugo定日镜在同轴式和离轴式倾斜策略下的年均溢出效率，得到结论是离轴式倾斜策略的效率比同轴式更高，但离轴式倾斜的效果依赖于倾斜时刻的选取。抛物面式倾斜策略利用抛物面的聚光特性，将各子镜倾斜安装以拟合特定的抛物面，从而达到减小反射光斑效果的目的。Buck等^[6]通过仿真列举计算了不同倾斜时刻静态离轴倾斜策略和不同参数下的抛物面倾斜策略，结果表明抛物面式倾斜策略获得了更大的年均溢出效率提升效果，但是没有提出有效的优化方法来获取最优的抛物面参数。

在接收器的优化设计中，现有的研究大多聚焦于新型材料和物理结构的研发，以在工艺层面达到换热效率的提高或接收器成本的降低，较少研究针对特定结构的接收器，根据电站设计要求，对接收器关键参数进行优化设计。20世纪90年代，Steinfeld等^[8]提出了半经验方法来确定孔腔式接收器面积和介质温度，并利用蒙特卡洛光线追踪法对比了太阳形状对结果的影响，但是研究的电站规模较小，同时未考虑镜场效率。Luo等^[9]在对塔式太阳能热电站的整体设计时考虑了接收器子系统，将塔高和接收器面积作为决策变量之一，但镜场聚光模型和接收器热转换模型较为简单，且未考虑溢出损失，模型准确度较低。Carrizosa等^[10]对镜场进行优化时，考虑了塔高和接收器面积对镜场的光学效率的影响，并采用迭代求解的方法，同时优化了定日镜和接收器的参数，但在模型中并未考虑接收器的换热效率而只考虑了镜场效率，结果不够准确。

可以看到，现有的研究缺乏系统、高效的优化方法对定日镜场和接收器进行综合优化设计。本研究提出了一种聚光集热系统的综合优化方法，首先基于最优抛物面式子镜倾斜策略，对定日镜子镜倾斜方式进行优化，减少定日镜场的溢出损失，然后通过对接收器换热过程建模，提出了最小化平准化接收器度电成本的优化模型，基于子镜倾斜优化后的镜场对接收器关键参数进行优化设计，提高发电效率的同时降低发电成本。

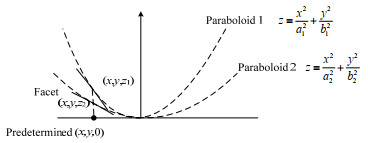
2 抛物面子镜倾斜优化

抛物面式倾斜安装方法能够利用抛物面的聚光性能，但是对于不同位置的定日镜，以及变化的太阳入射方向，如何选取最优的固定抛物面形状来获得最小的溢出损失，需要通过优化方法来确定。因此，本研究提出的最优抛物面子镜倾斜方式(optimal paraboloid)优化模型如下：

$ \mathop {\min }\limits_{{a_h}, {b_h}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_t^{} {\sum\limits_i^{} {(1 - \frac{{E_{t, i}^{\rm{in}}({a_h}, {b_h})}}{{E_{t, i}^{}({a_h}, {b_h})}})} } $

(1)

式中：下标h为定日镜编号；a_h, b_h为抛物面参数；${E_{t, i}}({a_h}, {b_h})$和$E_{t, i}^{\rm{in}}({a_h}, {b_h})$分别为第i面子镜按照(a_h, b_h)决定的抛物面倾斜时，在第t个采样时刻反射的总能量和反射到接收器区域内的总能量，J。定日镜子镜按照抛物面倾斜的示意图如图 2所示，子镜在整体镜面坐标系下的x，y坐标根据子镜划分方式和子镜大小确定，z坐标和法向根据抛物面参数决定，具体计算公式参考文献[11]。

目标函数的计算需要对镜面反射能量进行仿真，研究采用蒙特卡洛光线追踪法^[12]，该方法使用蒙特卡洛方法来刻画太阳能量分布，在太阳光锥中选取光线并根据太阳能量分布计算光线能量，并使用光线追踪法计算每根光线在入射和定日镜反射过程中的各项能量损失，计算得到最终在接收器平面内的反射能量分布，在接收器区域内进行积分计算得到接收器接收到的有效能量和溢出损失。由于光线追踪法无解析表达式，而且蒙特卡洛法需要大量撒点计算以保证精度，导致目标函数计算成本较大。因此上述优化问题采用一种结合粒子群算法和信赖域算法的2阶段寻优算法来快速求解，求解具体过程可参考文献[11]。

3 接收器优化设计 3.1 接收器建模

定日镜场反射到接收器上的能量，除了传递给传热介质外，还会发生反射、辐射等各项热损失。接收器按照物理结构可以划分为孔腔式和外露式2种接收器，外露式接收器的面板直接暴露在空气中，而孔腔式接收器则将接收器面板安装在塔顶的孔腔内，为不失一般性，本研究将对孔腔式接收器换热过程进行建模。

首先建立接收器发生的热量交换过程的热损失模型如式(2)所示：

$ {Q_{\rm{total}}} = {Q_{{\rm{loss, ref}}}} + {Q_{{\rm{loss, conv}}}} + {Q_{{\rm{loss, rad}}}} + {Q_{{\rm{loss, cond}}}} + {Q_{\rm{f}}} $

(2)

式中：${Q_{{\rm{total}}}}$为定日镜场汇聚的能量功率，W；${Q_{\rm{loss, ref}}}$、${Q_{{\rm{loss, conv}}}}$、${Q_{{\rm{loss, rad}}}}$和${Q_{{\rm{loss, cond}}}}$分别为反射热损失功率、对流热损失功率、辐射损失功率和传导热损失功率，W；$ {Q_{\rm{f}}} $为传热给传热介质的功率，W。

接着建立接收器换热过程的能量平衡方程为

$ {Q_{\rm{f}}} = {q_m}_{\rm{f}}({h_{{\rm{out}}}} - {h_{{\rm{in}}}}) $

(3)

式中：$ {q_m}_{\rm{f}} $为传热介质的质量流量，kg⋅s⁻¹；$ {h_{{\rm{in}}}} $和${h_{{\rm{out}}}}$分别为接收器入口和出口传热介质的焓值，J⋅kg⁻¹。另外，可以列出基本换热方程如下：

$ Q_{\mathrm{f}}=\frac{T_{\mathrm{w}, \mathrm{o}}-T_{\mathrm{w}, \mathrm{i}}}{\frac{\delta_{\mathrm{w}}}{\lambda_{\mathrm{w}} A_{\mathrm{m}}}}=\frac{T_{\mathrm{w}, \mathrm{i}}-T_{\mathrm{f}}}{\frac{1}{\alpha_{\mathrm{f}} A_{\mathrm{i}}}}=\frac{T_{\mathrm{w}, \mathrm{o}}-T_{\mathrm{f}}}{\frac{\delta_{\mathrm{w}}}{\lambda_{\mathrm{w}} A_{\mathrm{m}}}+\frac{1}{\alpha_{\mathrm{f}} A_{\mathrm{i}}}} $

(4)

$ A_{\mathrm{m}}=\pi d_{\mathrm{m}} L=\pi \frac{d_{\mathrm{o}}-d_{\mathrm{i}}}{\ln \left(d_{\mathrm{o}} / d_{\mathrm{i}}\right)} L $

(5)

$ {A_{\rm{i}}} = {\rm{ \mathit{ π}}} {d_{\rm{i}}}L $

(6)

$ {T_{\rm{f}}} = \frac{{{T_{{\rm{in}}}} + {T_{{\rm{out}}}}}}{2} $

(7)

式中：T_{w, o}和T_{w, i}分别为接收器换热管外壁和内壁温度，K；T_f为传热介质平均温度，K；d_o，d_i，d_m分别为接收器管道外径、内径和平均直径，m；A_m和A_i分别为接收器管壁平均导热面积和内壁导热面积，m²；L为换热管的长度，m；δ_w为管壁厚度，m；T_in和T_out分别为传热介质的入口和出口温度，K；λ_w为换热管导热系数，W⋅m⁻¹⋅K⁻¹；α_f为传热介质在接收器管道内对流传热的传热系数，W⋅m⁻²⋅K⁻¹，使用因次分析法计算得到。

反射热损失功率计算式如下：

$ {Q_{{\rm{loss, ref}}}} = {\rho _{{\rm{rec}}}}{Q_{{\rm{total}}}}F $

(8)

$ F = \frac{{{A_{{\rm{rec}}}}}}{{{A_{{\rm{ape}}}}}} $

(9)

式中：ρ_rec为接收器面板的反射率，由接收器面板的材质和表面分布情况决定。对于孔腔式接收器，由于孔腔的存在，导致一部分反射的能量在孔腔内多次反射，最终又有部分被吸收，为了简化计算，采用可视因子校正，即式(8)中的$F$，具体定义如式(9)所示，其中A_rec和A_ape分别为接收器换热面板和孔腔的面积，m²。对于外露式接收器，可视因子为1。

辐射热损失的计算方式如下：

$ Q_{\text {loss, rad }}=\varepsilon_{\mathrm{m}} \sigma\left(T_{\mathrm{w}, \mathrm{o}}^{4}-T_{\text {air }}^{4}\right) A_{\mathrm{rec}} F $

(10)

$ {\varepsilon _{\rm{m}}} = \frac{{{\varepsilon _{\rm{w}}}}}{{{\varepsilon _{\rm{w}}} + (1 - {\varepsilon _{\rm{w}}})F}} $

(11)

式中：ε_w为接收器管壁的辐射系数；ε_m为对孔腔进行修正后得到的平均辐射系数；σ为玻尔兹曼常数，W⋅m⁻²⋅K⁻⁴；T_air为环境空气温度，K。

对流热损失的计算方式如下：

$ {Q_{{\rm{loss, conv}}}} = {\alpha _{{\rm{air}}}}({T_{{\rm{w, o}}}} - {T_{{\rm{air}}}}){A_{{\rm{ape}}}} $

(12)

式中：α_air为空气的对流传热系数，W⋅m⁻²⋅K⁻¹；分为自然对流传热系数α_{air, nc}和强制对流传热系数α_{air, fc}，即

$ {\alpha _{{\rm{air}}}} = {\alpha _{{\rm{air, nc}}}} + {\alpha _{{\rm{air, fc}}}} $

(13)

α_{air, fc}使用因次分析法计算，相应的经验公式为

$ N u_{\text {air, fc }}=0.028\;7 {Re}_{\text {air }}^{0.8} P r_{\text {air }}^{1 / 3} $

(14)

$ \alpha_{\text {air }, \text { nc }}=0.81\left(T_{\text {w, } 0}-T_{\text {air }}\right)^{0.426} $

(15)

式中：Nu_{air, fc}、Re_air和Pr_air分别为空气强制对流传热的努塞尔数、雷诺数和普朗特数。

传导热损失主要是通过隔热材料的热损失：

$ Q_{\text {loss , cond }}=\frac{\left(T_{\mathrm{w}, \mathrm{o}}-T_{\text {insu }}\right)}{\frac{\delta_{\text {insu }}}{\lambda_{\text {msu }}}} A_{\text {rec }}=\frac{T_{\text {insu }}-T_{\text {air }}}{\frac{1}{\alpha_{\text {air, insu }}}} A_{\text {rec }} $

(16)

式中：T_insu、δ_insu、λ_insu分别为隔热层的表面温度(K)、厚度(m)和传热系数(W⋅m⁻²⋅K⁻¹)；α_{air, insu}为空气与隔热层的传热系数，W⋅m⁻²⋅K⁻¹。同样使用因次分析法计算，采用的经验计算公式为

$ N u_{\text {air }}=0.027\;9 {Re}_{\text {air }}^{0.805} P r_{\text {air }}^{0.45}\left(0.785 T_{\text {insu }} / T_{\text {air }}\right)^{0.2} $

(17)

式中：Nu_air为空气对流传热的努塞尔数。

联立方程(2)~(17)可以求解得到当定日镜汇聚能量确定时，最终传递给传热介质的热量。上述联立方程通过迭代法求解。

3.2 接收器优化设计模型

为了在电站的设计阶段综合考虑定日镜场和接收器的效率，同时降低电站的建设成本，本研究参照电站设计时常用的平准化度电成本(levelized cost of energy，LCOE)指标，设计了平准化接收器度电成本(levelized receiver cost of energy，LRCOE)指标如下：

$ \mathrm{LRCOE}=\frac{\left[\frac{I_{\mathrm{debb}}\left(1+I_{\mathrm{debt}}\right)^{y}}{\left(1+I_{\mathrm{debt}}\right)^{y}-1}+I_{\text {insurance }}\right] C_{\text {invest }, \mathrm{rec}}+C_{\mathrm{O} \& \mathrm{M}, \mathrm{rec}}}{W} $

(18)

式中：I_debt和I_insurance分别为每年的利率和保险费率；C_{invest, rec}和C_{O & M, rec}分别为接收器的总投资成本和操作维护成本，$；W为年均发电量，kW⋅h；y为电站全生命周期，a。

在接收器子系统的优化设计过程中，传热介质流量和出入口温度通常由发电模块决定。从上文的研究中可以看出，接收器的孔腔面积决定了溢出效率，而接收器面板的换热面积和接收器换热管直径决定了换热效率。因此，在接收器的优化模型中，保持接收塔高度和定日镜场布局参数不变，决策变量定为接收器孔腔的长l_ape、宽w_ape、面板的长l_rec和宽w_rec、换热管的外径d_o，其中接收器孔腔长宽决定了镜场的溢出效率，面板的长和宽决定了接收器的换热面积，换热管内径决定管内传热介质的流动状态，对接收器的换热效率具有决定影响。接收优化目标是最小化LRCOE。建立的优化模型如下：

$ \min\limits_{l_{\mathrm{rec}}, w_{\mathrm{rec}}, l_{\text {ape }}, w_{\text {ape }}, d_{\mathrm{o}}} \text { LRCOE } $

(19a)

$ {\rm{s.t.}}\;\;\;\;\;{l_{{\rm{rec}}}} \geqslant {l_{{\rm{rec, lb}}}} $

(19b)

$ {w_{{\rm{rec}}}} \geqslant {w_{{\rm{rec, lb}}}} $

(19c)

$ {l_{{\rm{ape}}}} \geqslant {l_{{\rm{ape, lb}}}} $

(19d)

$ {w_{{\rm{ape}}}} \geqslant {w_{{\rm{ape, lb}}}} $

(19e)

$ {d_{\text{o}}} \geqslant {d_{{\rm{o, lb}}}} $

(19f)

$ {l_{{\rm{rec}}}} \times {w_{{\rm{rec}}}} \times 0.5{P_{{\rm{limit}}}} \geqslant {P_{\rm{N}}} $

(19g)

$ W \geqslant {W_{{\rm{design}}}} $

(19h)

其中，式(19b)~(19f)为各参数的下限约束；式(19g)为接收器面板上的能量密度上限约束；下标lb为下界；P_N为额定工况下的接收器平均能量密度，W⋅m⁻²；P_limit为接收器上的能量密度安全上限，由接收器面板材质决定。理论上讲，优化模型应该限制每个时刻接收器上的峰值能量密度小于安全上限，但是在目标函数在计算接收器上总能量时，为了节约计算时间，并未采取聚焦优化策略，而文献[13]中4个聚焦点聚焦优化后的峰值能量密度是平均能量密度的2倍，具有一定参考性，所以在约束条件中设定额定工况下的平均能量密度小于能量密度上限的1/2，给予实时聚焦优化充分的实现空间。式(19h)表示年发电量的最低要求；${W_{design}}$为设计年发电量，kW⋅h。

4 求解方法

上述目标函数计算全年发电效率时，需要使用蒙特卡洛光线追踪法计算镜场反射能量，因此存在无解析表达式且计算耗时的问题，传统的基于梯度的优化方法不再适用。无梯度的优化方法中，随机优化方法是一类重要的优化方法，其思想是在可行域内随机撒点后，通过启发式的操作进行迭代寻优^[14]。粒子群算法就是其中典型的一种，其启发式搜索的灵感来源于鸟类觅食的过程，由于粒子群算法结构简单，易于实现，且具有良好的收敛性，因此研究选择粒子群算法来求解上述优化问题，并通过罚函数方法将上述有约束优化问题转换成粒子群算法易于求解的无约束优化问题^[14]。然而粒子群算法每次迭代需要计算种群中所有粒子的目标函数值，计算费时。

粒子群算法用集合$X = \left\{ {{x_j}\left| {j = 1, 2, \cdots n} \right.} \right\}$来表示粒子群，其中x_j为粒子，n为粒子总数，粒子进化的公式为

$ v_{j, d}^{k + 1} = \omega v_{j, d}^k + {c_1}r_1^k({\rm{pbest}}_{j, d}^k - x_{j, d}^k) + {c_2}r_2^k({\rm{gbest}}_{j, d}^k - x_{j, d}^k) $

(20)

$ x_{j, d}^{k + 1} = x_{j, d}^k + v_{j, d}^{k + 1} $

(21)

其中，$ x_{j, d}^k $和$ v_{j, d}^k $分别为第j个粒子的第d维分量在第k次迭代的位置和速度，$ {\rm{pbest}}_j^k $为第j个粒子k次迭代内发现的自身历史最佳位置，$ {\rm{gbest}}_{j, d}^k $表示粒子群在k次迭代内发现的全局最佳位置，ω为惯性系数，c₁和c₂分别为个体学习因子和全局学习因子，$ r_1^k $和$ r_2^k $为0~1的随机数。

为了平衡粒子群算法前期的全局探索性能和后期的快速收敛能力，Zhan等^[15]提出了基于迭代状态动态改变PSO算法参数的方法，结构简单易于实现，且仿真结果表明对不同特性的优化问题都有着较好的加速效果，因此本研究采用了这种方法，并将智能蒙特卡洛采样方法与之结合，提出了一种智能蒙特卡洛采样的自适应粒子群算法(smart sampling Monte Carlo adaptive PSO，SSMC-APSO)。

研究采用的自适应粒子群算法的基本原理是根据算法迭代处于的不同状态采取不同的参数更新策略。首先将迭代过程划分为以下4种状态：

1) 探索状态(exploration)，粒子分布比较散乱，没有明显的中心。

2) 挖掘状态(exploitation)，由于学习机制的存在，粒子开始朝着最优点运动。

3) 收敛状态(convergence)，粒子集中收敛在最优点附近。

4) 跳出状态(jumping out)，若最优粒子从一个局部最优点迭代到了另一个局部最优点，此时其他粒子距离最优点较远，会重新经历收敛过程，从挖掘再到收敛。

如何设计相应的定性指标判断迭代状态以及在不同迭代状态相应的迭代参数的调整方式可以参照文献[15]，基本思想为在探索和跳出阶段采用较大的c₁和c₂及较小的ω，在收敛和挖掘阶段则相反。

由于目标函数计算使用的是蒙特卡洛光线追踪法，蒙特卡洛采样点数越大，计算结果越准确，而采样点数减少可以减少目标函数计算的时间成本。因此，在优化过程中，可以根据迭代状态以及当前点离最优点的距离来动态地调整计算精度，从而合理地分配计算资源，减少计算时间，提高寻优精度。具体的实施过程如下：对于粒子${x_j}$，计算其目标函数时所用的采样点数N_j由2部分决定，具体如下：

$ {N_j} = {N_{\rm{b}}} \times {\eta _j} $

(22)

其中：N_b为群体采样基数(sampling number base)，由粒子群算法迭代处于的不同状态进行相应的调整；η_j为粒子个体采样系数，由粒子当前位置和当前获得的全局最优位置的关系来决定。

N_b在不同迭代状态的调整策略包括快速增大、慢速增大、快速减小和慢速减小4种手段，具体实施如表 1所示：

1) 探索状态，此时应尽可能用更短时间计算更多的点以获取更多的信息，而计算精度要求相对不高，所以此时应该采用较小的精度以缩短计算时间，采样基数N_b应该慢速减小；

2) 挖掘状态，此时各粒子趋向于各自的历史最优点附近，为充分挖掘粒子周围的信息，应该增加蒙特卡洛仿真精度，确保粒子个体能够收敛到最优值，因此应慢速增大N_b；

3) 收敛状态，此时粒子处于寻找全局最优的阶段，粒子位置比较集中，目标函数差异也相对较小，应增大精度来减少计算误差以保证最后的收敛，因此应该快速地增大N_b；

4) 跳出状态，全局最优粒子跳出局部最优之后，其他粒子离它较远，函数值差异也相应增大，此时应降低目标函数的计算精度，加快状态转变，因此应该快速减小N_b。

假设初始采样基数为$N_{\rm{b}}^0$，第k次迭代的采样基数为$N_{\rm{b}}^k$，则${N_{\rm{b}}}$在各个迭代状态的调整策略如表 1所示。其中，$\mu $和$\nu $分别为慢速和快速增大或减小的速度因子，r为(0, 1)之间的随机数，用于增加蒙特卡洛采样点数的随机性，符合粒子群算法搜索的随机特性，提高求解的成功率，同时也对算法判断粒子群迭代状态具有更高容错性，增强算法的鲁棒性。对N_b设定变化过程的上下限，以保证不会因为仿真精度太低导致目标函数计算超出误差限，且整体仿真计算时间不会过长。

粒子个体采样系数η_j的调整策略是基于粒子当前位置与当前最优点的距离来确定，定义粒子x_j距离当前最优点x_gb的距离$ {{\mathit{\Delta }} _j} = \sum\limits_{d = 1}^D {{{(x_{j, d}^k - x_{{\rm{gb}}, d}^k)}^2}} $，其中D为粒子维度。η_j的计算式为

$ {\bar {\mathit{\Delta }} _j} = \frac{{{{\mathit{\Delta }} _j} - {{\mathit{\Delta }} _{{\rm{min}}}}}}{{{{\mathit{\Delta }} _{{\rm{max}}}} - {{\mathit{\Delta }} _{{\rm{min}}}}}} $

(23)

$ {\eta _j} = \frac{{{1 \mathord{\left/ {\vphantom {1 {({{\bar {\mathit{\Delta }} }_j} + \tau )}}} \right. } {({{\bar {\mathit{\Delta }} }_j} + \tau )}}}}{{\sum\limits_{j = 1}^{n'} {{1 \mathord{\left/ {\vphantom {1 {({{\bar {\mathit{\Delta }} }_j} + \tau )}}} \right. } {({{\bar {\mathit{\Delta }} }_j} + \tau )}}} }} \times n' $

(24)

式中：$ {\bar {\mathit{\Delta }} _j} $为粒子x_j距离x_gb的归一化距离，Δ_min和Δ_max分别为Δ_j的最小值和最大值，所以${\bar {\mathit{\Delta }} _j} \in [0, 1]$。τ为平衡因子，τ越小，采样点数与距离大小的相关性越强。$ n' $为位于可行域内的粒子数目。这样的算式能使离最优粒子最近的粒子获得更多的采样数，但是平均采样点数为N_b。

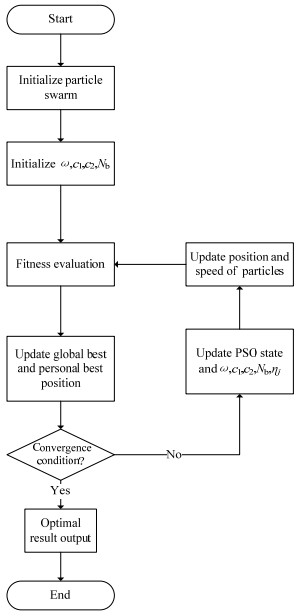
综上所述，采用智能采样蒙特卡洛方法的自适应粒子群算法流程如图 3所示。

5 结果分析 5.1 子镜倾斜优化结果

为了验证上述方法的有效性，研究选取西班牙PS10塔式太阳能热电站作为仿真对象，电站的主要参数如表 2所示，并选取了表 3所示的镜场中5面定日镜进行子镜倾斜优化前后对比。在特定的接收器面积下，上述5面定日镜在不同子镜倾斜策略下的年均溢出损失如表 4所示。从表中可以看到，本研究提出的抛物面式倾斜优化得到的结果相对原始平面镜的溢出损失大大减少，同时减小效果也远大于同轴式倾斜策略。与动态离轴式倾斜相比虽有一定差距，但随着定日镜距离增加，差距减小较为明显，在较远距离下，二者的溢出损失差距只有3%，作为固定面形的定日镜倾斜方式能够达到与动态倾斜较为接近的溢出效率，验证了最优抛物面倾斜优化的有效性。

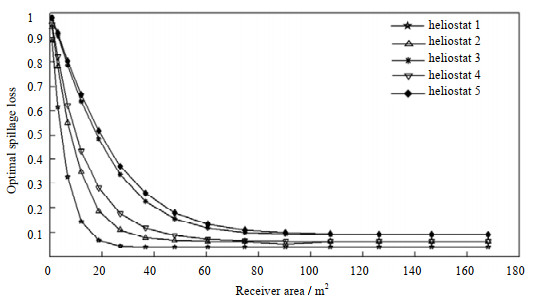
5面定日镜在不同的接收器面积参数下，优化得到的年均溢出损失如图 4所示。可以看到，离接收器较远的5号定日镜相对1、3号来说需要更大的接收器面积达到同样的溢出效率，在接收器侧面的4、5号定日镜虽然与2、3号定日镜离接收器的距离相差较小，但需要的接收器面积较大，这是因为成像角度较差，定日镜反射光斑大多是细长形的，导致溢出损失较大。

从上述结果中可以看出，最优抛物面子镜倾斜策略能够有效地减少溢出损失，但不同位置的定日镜需要的接收器面积不同，对接收器面积等关键参数需要综合考虑镜场和接收器的效率。

5.2 接收器优化结果

同样以PS10电站为例对上述方法进行仿真验证。PS10电站的接收器成本计算，研究采用文献[2]中的经验公式，具体如表 5所示，H为接收器中心离地面高度，而发电量计算中需要的发电模块的效率，基于文献[4]给出的额定工况下的发电模块效率以及文献[16]给出的非额定工况下的拟合公式。

表 6列出了在电站原始参数下的文献结果以及接收器优化前后的仿真结果。可以看出，定日镜场光学效率和接收器效率仿真结果较为准确，验证了模型的准确性，发电模块效率误差较大，这是因为文献中的发电模块全年效率和额定工况下的发电效率相等，而在本研究的模型中非额定工况下的发电功率有所降低，更加符合实际情况。可以看到，在PS10原始镜面参数下，对接收器的优化结果增大了接收器孔腔面积，从而减小了溢出损失，提高镜场光学效率；另外减小了换热面板的大小，从而减少成本的同时弥补了孔腔变大带来的换热效率降低。由于定日镜反射光斑较大，溢出效率和接收器的换热效率难以兼顾，使得总发电量的提升有限，最终LRCOE的降低也不是很大。

5.3 综合优化结果

对PS10镜场中的定日镜进行子镜倾斜优化设计后，再对电站的接收器参数进行优化。值得注意的是，对于不同大小的接收器孔径，定日镜的最优抛物面倾斜策略应该有所不同，这就使原优化问题变成了多层优化问题，外层对接收器参数进行寻优，内层对特定接收器参数下寻优子镜倾斜方式。由于子镜倾斜方式寻优过程较长，为了简化问题，首先采用固定的小面积接收器参数对定日镜子镜倾斜进行优化，然后固定PS10镜场的子镜倾斜方式不变，再来寻优接收器参数。

得到的结果如表 7所示，可以看到，加入了子镜倾斜策略后，镜场在小面积的接收器下依然能够提供较大的聚光效率和总能量，对接收器的优化结果相对原始接收器面板面积相对减小45.4%，但是镜场的光学效率只下降1.2%，年发电量下降1.57%，依然在较高的水平。接收器面积的减小使得换热效率变得更高，上述因素综合作用，使接收器的度电成本降低14.8%。值得一提的是，对接收器的子镜倾斜优化并不会带来额外的建造成本，因此可以看到，采用了聚光集热系统的优化设计方法，电站的准度电成本将会显著降低。

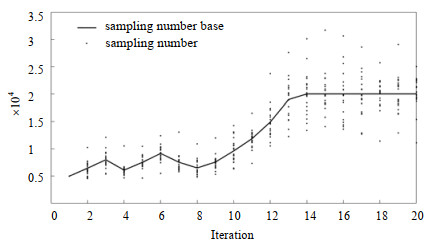
迭代过程中采样点数变化如图 5所示，其中横坐标代表迭代次数，曲线代表每一代粒子采样数目的基数${N_{\rm{b}}}$，在曲线上下分布的点代表各粒子的具体采样点数。可以看到，采用智能采样方法后，一方面采样点基数随着迭代状态改变，在前期探索过程中，使用较低精度减少整体的计算时间，并能够在挖掘阶段适当地提高精度，提高寻优效率，当算法趋于收敛时，采样数目慢慢达到设定的上限，使得算法最终高精度地计算并收敛到最优值；另一方面，各个粒子可以根据粒子距离最优粒子的远近动态分配不同的采样点数，在最优点附近采用高精度计算而在最优点较远的位置采用较小精度，使得计算时间的分配更加合理，算法对目标函数计算的效率更高，整体耗时更少。

不同算法的求解结果以及求解过程的性能指标如表 8所示。从迭代的最优结果来看，各个算法获得的最优解相差不大，在多次重复实验中都能找到最优解，可以看到，APSO相对PSO来说成功率和迭代时间都有较大提升，而加入智能蒙特卡洛采样的方法后，粒子群算法的整体消耗时间变少。表中成功率的定义为在重复多次寻优，在不同的随机初始种群下，算法能够迭代收敛到最优值的比率，通过20次重复实验获得，可以看到，得益于在最优点附近的蒙特卡洛采样精度更高，SSMC-APSO方法的成功率有了显著提升，最优解的目标函数也是所有算法中最优的。

6 总结

本研究从定日镜子镜倾斜优化和接收器优化2个方面，对塔式太阳能热电站聚光集热系统进行了优化设计。最优抛物面子镜倾斜策略大大减少了定日镜的反射能量的溢出损失，而在接收器的设计过程中综合考虑了定日镜场的溢出效率以及接收器的换热损失和建造成本，并提出了一种结合了智能蒙特卡洛采样策略的自适应粒子群算法快速求解，优化后的接收器换热效率更高，成本更低，给电站的发电效率提升和成本降低带来了显著效果。未来的工作可以聚焦于更加系统的优化方法，在电站的设计阶段综合考虑镜场布局和接收器结构等，保证寻优获得电站的整体效率最优解。