芦丁与山奈酚-3-O-芸香糖苷是苦荞的主要活性组分,具有改善毛细血管微循环及增加单胺类神经递质含量等功效,临床上可用于高血压和老年痴呆等疾病的治疗[1-2]。以超临界二氧化碳(SC-CO2)为萃取及反应介质的超临界流体色谱(SFC)技术,具有绿色环保、传质效率高等优势[3],在中药有效成分分离提纯方面具有良好的发展前景。目前SFC提纯工艺多以芦丁单一组分为主[4],对山奈酚-3-O-芸香糖苷报道较少。以两者为共同目标进行提纯可以最大限度发挥药效,满足市场需求。
在开发基于SFC的芦丁与山奈酚-3-O-芸香糖苷活性组分工业提纯技术的过程中,扩散系数是工程放大、设计及优化必不可少的关键基础数据[5]。因此,有必要开展相关溶质组分在SC-CO2体系中扩散系数的测定及预测研究。但CO2属于非极性分子,对芦丁与山奈酚-3-O-芸香糖苷等极性组分的溶解效果较差,为解决这一问题,需要加入适量的乙醇或甲醇等改性剂,以增强SC-CO2对极性物质的溶解能力[6-7],提高提取效率。目前对于扩散系数的研究多数局限于溶质在SC-CO2体系中的二元扩散系数,对于处在SC-CO2/改性剂体系下三元扩散系数的文献报道较少,在一定程度上限制了SFC等分离技术的工业推广[8]。
本文拟采用色谱峰扩展法(Taylor峰扩展法),对超临界二氧化碳-甲醇(SC-CO2/CH3OH)体系下,芦丁与山奈酚-3-O-芸香糖苷活性组分的三元扩散系数进行测定,考察扩散系数随压力、温度、密度及夹带剂质量分数变化的影响规律,并采用不同的经验方程对各个变量进行关联及误差分析。在此基础上,采用修正的Wilke-Chang模型[9]、He-1997模型[10]、Dymond-Hildebrand-Batschinski模型[11]对相关溶质分子在SC-CO2/CH3OH体系中的三元扩散系数进行预测,以理论计算与实验结果的平均绝对偏差(AAD)为指标评价各个模型的预测效果。
2 实验部分 2.1 实验方法测定溶质扩散系数的方法主要有Talyor峰扩展法、核磁共振响应法及示踪原子响应法等[12]。其中Talyor峰扩展法的原理是通过测定溶质出入口响应曲线的差异来获得扩散系数,该法可在较小的梯度推动力下测定溶质的扩散系数,具有测定精度高及耗时少等优点[13]。
采用Talyor峰扩展法测定扩散系数时,为保证扩散柱中的流体处于层流运动状态,流体流动的雷诺数Re需要满足式(1):
| $ Re = \frac{{du\rho }}{\mu } \le 2\;000 $ | (1) |
式中:d为扩散管内径;u为线速度;ρ为密度;μ为黏度。
扩散系数D12满足式(2)、(3):
| $ {D_{12}} = \frac{1}{4}u\left[ {H - {{\left( {{H^2} - \frac{{r_{\rm{i}}^2}}{3}} \right)}^{\frac{1}{2}}}} \right] $ | (2) |
| $ H = \frac{{LW_{1/2}^2}}{{5.545t_{\rm{R}}^2}} $ | (3) |
式中:H为理论板数;ri为扩散管内半径;L为扩散管长度;W1/2为半峰宽;tR为保留时间。
2.2 实验材料与装置实验材料:芦丁标准品(质量分数≥8.0%,大连美仑生物技术有限公司)、山奈酚-3-O-芸香糖苷标准品(质量分数≥98.0%,大连美仑生物技术有限公司)、食品级CO2(质量分数≥99.9%,天津浩伦气体有限公司)、无水甲醇(分析纯,科密欧化学试剂有限公司)。
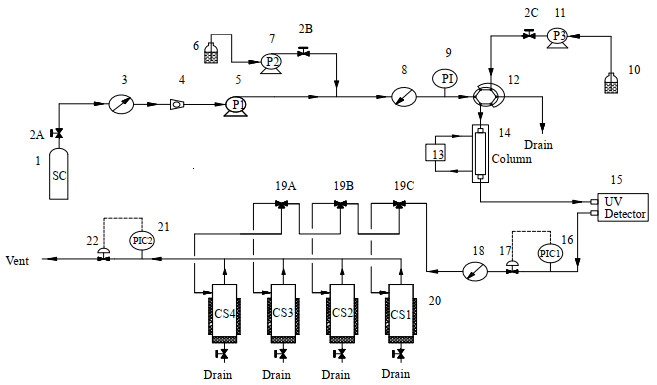
实验装置采用美国Thar公司的SFC-200型制备型超临界流体色谱,主要由进样系统、控压系统、扩散单元及色谱检测系统组成。其中扩散单元主要包括扩散管和恒温水浴,扩散管为不锈钢毛细管(规格1/16 cm×0.03 cm×1 500 cm,美国Upchurch公司),其盘绕为直径7.5 cm的螺旋盘管,具体参见图 1-超临界流体色谱装置流程图。
|
图 1 超临界流体制备色谱提纯工艺实验装置流程图 Fig.1 Experimental flowsheet of the purification technology using supercritical fluid preparation chromatography 1. CO2 tank 2A, 2B, 2C. switch valve 3. pre-heater 4. CO2 flow meter 5. CO2 feeding pump 6. modifier jar 7. modifier feeding pump 8. feeding flow meter 9. pre-column manometer 10. sample jar 11. automatic feeding pump 12. six-way valve 13. heat exchanger 14. Taylor dispersion tube 15. detector 16. post-column manometer 17. pressure regular valve 18. product cooler 19A, 19B, 19C. procedure control valve 20. product collecting tank 21. system manometer 22. back pressure valve |
实验测定条件:温度为308.15~323.15 K,压力为8~14 MPa,从CO2和甲醇二元体系相图中看[14],在此条件范围内没有发生相分离,溶质结构不会被破坏。流动相CO2质量流量为3 g×min-1,流动相中甲醇质量分数为16.5%,实验温度控制偏差±0.2 ℃,在此CO2流量实验条件下,可以有效消除扩散管中二次流对扩散系数测定结果的影响。
2.3 实验误差分析实验过程的误差来源为原料组分质量分数测定的相对误差、实验仪器的精确度以及实验操作造成的相对误差。因此为保证准确性,每组实验数据进行了至少3组平行实验,采用误差传递公式计算最终实验误差,实验结果标准偏差≤±5%。
3 扩散系数预测模型在实际工程设计中,即使溶质摩尔浓度达到5%(甚至达到10%),仍可视为无限稀释溶液,而超临界状态下,许多物质的溶解度不高(摩尔分数小于10-3)[15],因此,在SC-CO2/CH3OH体系下,芦丁与山奈酚-3-O-芸香糖苷溶液可视为无限稀释溶液。无限稀释扩散系数模型的建立尤为重要,通过建立模型可以对实验数据进行理论关联及预测。本文拟采用修正的Wilke-Chang模型、He-1997模型及Dymond-Hildebrand-Batschinski模型对芦丁与山奈酚-3-O-芸香糖苷组分在SC-CO2/CH3OH体系中的扩散系数实验数据进行关联计算,并通过AAD值对比确定适宜的预测模型。
Wilke-Chang模型是以流体力学理论为基础的预测模型,基础模型不考虑分子间的相互作用,但SC-CO2/CH3OH体系中,溶质与甲醇之间会存在缔合作用,因此在采用Wilke-Chang模型时,需进行必要的修正,修正后的公式如下:
| $ {D_{12}} = 7.4 \times {10^{ - 8}}{\left( {\sum {{w_i}} {\phi _i}{M_i}} \right)^{1/2}}T{\mu _2}V_{{\rm{m}}, {\rm{b}}1}^{ - 0.6} $ | (4) |
式中:wi为i组分质量分数;Φi为i组分缔合因子;Mi为i组分摩尔质量;T为体系热力学温度;μ2为溶剂黏度;Vm, b1为溶质泡点状态下的摩尔体积。
He-1997模型是在粗硬球理论与分子动力学模拟建立的模型基础上简化得到的,计算公式如下:
| $ {D_{12}} = A \times {10^{ - 10}}\left( {V_{{\rm{m}}, 2}^K - B} \right)\sqrt {\frac{T}{{{M_1}}}} $ | (5) |
| $ {\rho _2} \ge 1.2\left( {{\rho _2} = \frac{{{\rho _2}}}{{{\rho _{{\rm{c}}2}}}} = \frac{{{V_{{\rm{m}}, {\rm{c}}2}}}}{{{V_{{\rm{m}}, 2}}}}} \right), K = 1;\quad {\rho _2} < 1.2, K = 1 + \left( {{\rho _{{\rm{r}}2}} - 1.2} \right)M_2^{0.5} $ |
| $ {A = 0.616\;14 + 3.092\exp \left( { - 0.877\;56\frac{{\sqrt {{M_2}{V_{{\rm{m}}, {\rm{c}}2}}} }}{{{p_{c2}}}}} \right)} $ |
| $ {B \approx 23} $ |
式中:A,K为与溶剂相关的拟合参数;Vm, 2为溶剂摩尔体积;M1为溶质摩尔质量;ρr2为溶剂相对密度;ρc2为溶剂临界密度;Vm, c2为溶剂临界状态下摩尔体积;M2为溶剂摩尔质量;pc2为溶剂临界压力;B为常数。
Dymond-Hildebrand-Batschinski模型则是基于自由体积理论所提出的预测模型,具有β和Vm, D两个可调参数,扩散系数计算如式(6)所示:
| $ {D_{12}} = \beta {T^{0.5}}\left( {{V_{{\rm{m}}, 2}} - {V_{{\rm{m}}, {\rm{D}}}}} \right) $ | (6) |
式中:β为溶质、溶剂的性质相关联的可调参数;Vm, D为最小自由摩尔体积。
4 实验结果与讨论 4.1 芦丁及山奈酚-3-O-芸香糖苷组分扩散系数测定在温度为308.15~323.15 K、压力为8~14 MPa的实验条件下,采用色谱峰扩展法测得了芦丁及山奈酚-3-O-芸香糖苷组分在SC-CO2/CH3OH中的无限稀释扩散系数。
如表 1所示,芦丁及山奈酚-3-O-芸香糖苷组分在SC-CO2/CH3OH体系下扩散系数的范围分别为2.02× 10-8~3.46×10-8 m2×s-1及2.02x10-8 ~ 3.42×10-8 m2×s-1,与曹秋瑾[16]测定的香豆素等黄酮类化合物在SC-CO2/C2H5OH体系中的扩散系数具有相同的数量级。此外,与JABBARI等[17]采用色谱峰扩展法测得的黄酮类化合物在298.15 K液态甲醇中的扩散系数范围0.73×10-9 ~1.19×10-9 m2×s-1相比,SC-CO2/CH3OH体系下芦丁及山奈酚-3-O-芸香糖苷组分的扩散系数增加了一个数量级,进一步说明超临界流体优越的传质性能。
|
|
表 1 芦丁及山奈酚-3-O-芸香糖苷扩散系数测定数据表 Table 1 Diffusion coefficients of rutin and kaempferol-3-O-rutinoside |
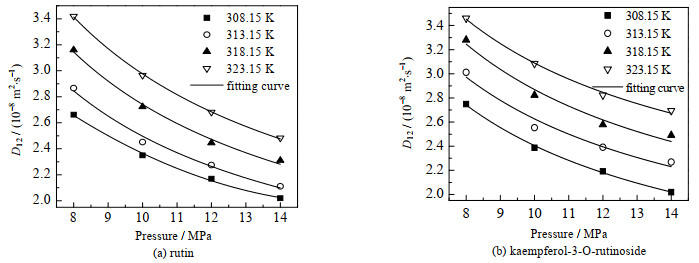
在温度一定的条件下,图 2测定了压力变化对芦丁及山奈酚-3-O-芸香糖苷扩散系数的影响。从图中可以看出:在不同温度条件下,芦丁及山奈酚-3-O-芸香糖苷组分的扩散系数均随着压力的升高而降低,主要因为当温度一定时,压力升高会使SC-CO2/CH3OH体系的密度升高,溶质分子扩散的自由体积减小,从而增加溶质与溶剂分子间的碰撞频率,溶质分子扩散的束缚增大,扩散系数降低;另外,还可以发现在低压区域溶质分子的扩散系数受压力的影响更加显著,因为在低压区密度受压力的变化更加敏感,而扩散系数与密度紧密相连,因此扩散系数降低更加显著。
|
图 2 SC-CO2/CH3OH体系下压力对溶质扩散系数的影响 Fig.2 Effects of pressure on diffusion coefficients in SC-CO2/CH3OH |
SUAREZ等[18]提出了压力与扩散系数的经验关联方程,如下式(7):
| $ {D_{12}} = {a_p} + {b_p}/p $ | (7) |
在实验数据的基础上,采用式(7)对扩散系数与压力进行关联,拟合结果及参数见表 2。由表 2可知,方程(7)的适用性较好,芦丁组分关联方程的相对平均误差(ARE)为0.24%~1.05%,山奈酚-3-O-芸香糖苷组分关联方程的ARE为0.38%~1.58%。
|
|
表 2 不同温度下扩散系数与压力关联式(7)的拟合结果表 Table 2 Fitting results between diffusion coefficients and pressures of equation (7) at different temperatures |
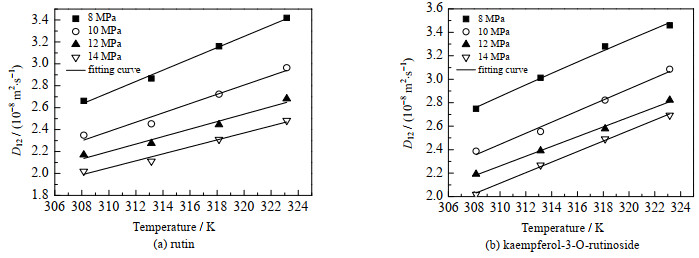
在压力一定的条件下,温度对芦丁及山奈酚-3-O-芸香糖苷扩散系数的影响如图 3所示。当压力不变时,芦丁及山奈酚-3-O-芸香糖苷组分的扩散系数随着温度的升高而增加。这主要由于温度的升高使密度降低,分子间距增大,溶剂对溶质分子的束缚作用减弱,有利于扩散。另外,温度升高还会使分子热运动加快,分子间相互作用力减小,进而导致芦丁及山奈酚-3-O-芸香糖苷的扩散系数增加。
|
图 3 SC-CO2/CH3OH体系下温度对溶质扩散系数的影响 Fig.3 Effects of temperature on diffusion coefficients in SC-CO2/CH3OH |
式(8)[19]可以对不同压力下温度与扩散系数的关系进行经验关联,结果如表 3所示:
|
|
表 3 不同压力下扩散系数与温度关联式(8)的拟合结果表 Table 3 Fitting results between diffusion coefficients and temperatures of equation (8) at different pressures |
| $ {D_{12}} = {a_T} + {b_T}T $ | (8) |
根据表 3可知:在实验范围内,芦丁及山奈酚-3-O-芸香糖苷的扩散系数与温度成线性关系,采用方程根据表 3可知:在实验范围内,芦丁及山奈酚-3-O-芸香糖苷的扩散系数与温度成线性关系,采用方程(8)对芦丁及山奈酚-3-O-芸香苷的扩散系数进行拟合,ARE分别为0.05%~1.15%、0.5%~1.87%,方程适用性较好;此外,随着压力增大,各个拟合方程的斜率逐渐降低,溶质扩散受温度的影响减弱,该结果与之前文献报道的超临界流体中扩散系数的变化趋势一致[20]。
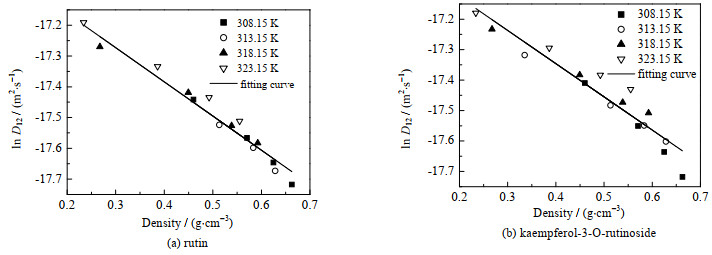
4.4 密度的影响图 4表示芦丁及山奈酚-3-O-芸香糖苷扩散系数随密度变化关系。体系的密度是通过Peng-Robinson状态方程及Van der Waals混合规则进行计算,其中涉及到的二元交互作用参数通过回归气液相平衡数据得到[21]。从图中可以看出,芦丁及山奈酚-3-O-芸香糖苷的扩散系数均随SC-CO2/CH3OH密度增加而呈现降低趋势。这是由于随着密度的增加,溶质分子周围聚集的溶剂分子数增加,溶质分子与溶剂之间的碰撞频率增加,不利于溶质分子的进一步扩散,导致其扩散系数逐渐降低。
|
图 4 SC-CO2/CH3OH体系下密度对溶质扩散系数的影响 Fig.4 Effects of density on diffusion coefficients in SC-CO2/CH3OH system |
表 4列出了扩散系数与密度经验关联式(9)[22]、(10)[23]的参数拟合结果,通过对比ARE可知,方程(10)的拟合精度要优于方程(9)。采用方程(10)对芦丁及山奈酚-3-O-芸香苷的扩散系数进行拟合,ARE分别为0.15%及0.19%,说明密度更趋于与扩散系数的对数呈线性关系。
|
|
表 4 扩散系数与密度关联式(9)、(10)的拟合结果表 Table 4 Fitting results between diffusion coefficients and density of equations (9) and (10) |
| $ {D_{12}} = {a_\rho } + {b_\rho }\rho $ | (9) |
| $ \ln {D_{12}} = {a_\rho } + {b_\rho }\rho $ | (10) |
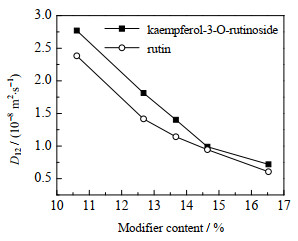
根据相关文献报道[24-26],夹带剂的加入会对溶质的扩散系数产生明显影响。在SC-CO2/CH3OH体系下,芦丁及山奈酚-3-O-芸香糖苷组分的扩散系数随夹带剂甲醇质量分数的变化如图 5所示。
|
图 5 SC-CO2/CH3OH体系下夹带剂质量分数对溶质扩散系数的影响 Fig.5 Effects of modifier content on the diffusion coefficients of solute in SC-CO2/CH3OH system |
从图 5中可以看出,芦丁及山奈酚-3-O-芸香糖苷组分的扩散系数均随着夹带剂甲醇质量分数的增加而降低。一方面,夹带剂甲醇会与溶质分子发生氢键相互作用,缔合形成新的扩散主体,随着甲醇质量分数不断增加,缔合程度逐渐增强,形成的新扩散主体体积也随之不断增大;另一方面,甲醇质量分数不断增加也会导致流动相密度增加,溶质分子受到束缚,分子碰撞频率提高。由于上述因素的共同作用,芦丁及山奈酚-3-O-芸香糖苷组分的扩散系数随着夹带剂甲醇质量分数的增加而呈下降趋势。另外,在相同条件下,山奈酚-3-O-芸香糖苷分子的扩散系数均高于芦丁分子的扩散系数,这主要因为扩散速率在一定程度上也会受到溶质分子大小及结构的影响。2个溶质组分的分子结构相似,但相比山奈酚-3-O-芸香糖苷,芦丁分子中多了一个羟基官能团,更容易与甲醇形成氢键,不利于扩散,因此芦丁的扩散系数低于山奈酚-3-O-芸香糖苷的扩散系数。
4.6 模型关联与预测以实验数据为基础,本文分别采用修正的Wilke-Chang模型、He-1997模型及Dymond-Hildebrand-Batschinski模型,对SC-CO2/CH3OH体系中芦丁及山奈酚-3-O-芸香糖苷组分的三元扩散系数进行了理论关联及预测,通过模型计算值与实验测定数据对比计算,得到平均绝对偏差(AAD),以判断并评价各个模型的预测效果。表 5和6分别给出了溶质和溶剂的模型关联参数及各个模型计算的AAD。
|
|
表 5 溶质溶剂的模型关联参数 Table 5 Related parameters for model correlation |
|
|
表 6 模型预测平均绝对偏差 Table 6 AAD results of different models |
从表 6中各模型预测平均绝对偏差结果可以看出,Dymond-Hildebrand-Batschinski模型预测计算结果的AAD最小,往后依次为He-1997模型、修正的Wilke-Chang模型。原因分析:对于修正的Wilke-Chang模型,溶质与甲醇缔合后溶质体积增大等因素对计算结果影响较大[15],因此AAD较大,预测效果最差;He-1997模型主要基于粗硬球理论与分子动力学,对于相关溶质组分在SC-CO2/CH3OH体系中扩散系数的预测效果优于修正的Wilke-Chang模型;Dymond-Hildebrand-Batschinski模型属于双参数可调模型,β和Vm, D与溶质及溶剂的性质相关联,可以根据SC-CO2/CH3OH体系下,溶剂及溶质的性质变化进行调整,因此,采用Dymond-Hildebrand-Batschinski模型对SC-CO2/CH3OH体系中的芦丁及山奈酚-3-O-芸香糖苷组分的三元扩散系数计算预测,结果最佳。
5 结论采用色谱峰扩展法,测定了芦丁及山奈酚-3-O-芸香糖苷在SC-CO2/CH3OH中的三元扩散系数。在此基础上,探究了压力、温度、流动相密度及夹带剂等因素对溶质分子芦丁及山奈酚-3-O-芸香糖苷扩散系数的影响规律,并通过3种模型对溶质分子在SC-CO2/CH3OH中三元扩散系数进行了理论关联及预测,主要结论如下:
(1) 在温度为308.15~323.15 K、压力为8~14 MPa及夹带剂甲醇质量分数为16.5 %的实验条件下,用色谱峰扩展法测得了芦丁组分的扩散系数范围为2.02×10-8~3.46×10-8 m2×s-1,山奈酚-3-O-芸香糖苷组分的扩散系数范围为2.02×10-8~3.42×10-8 m2×s-1。
(2) 芦丁及山奈酚-3-O-芸香糖苷组分在SC-CO2/CH3OH中的三元扩散系数随温度升高而增加,而随压力、密度及夹带剂甲醇质量分数升高而降低。
(3) 芦丁与山奈酚-3-O-芸香糖苷组分扩散系数的影响因素经验关联结果表明:压力经验关联式
(4) Dymond-Hildebrand-Batschinski模型对三元扩散系数的预测效果最佳,芦丁与山奈酚-3-O-芸香糖苷组分的AAD分别为2.48%和3.71%,优于修正的Wilke-Chang及He-1997模型。
符号说明:
|
|
| [1] |
宋晚平, 薛迎春.一种苦荞芦丁的提取分离方法: CN, 103833808A[P]. 2016-03-02. SONG W P, XUE Y C. A method for extraction and separation of tartary buckwheat rutin: CN, 103833808A[P]. 2016-03-02. |
| [2] |
何远景. HPLC法测定牛耳枫中山奈酚-3-O-芸香糖苷的含量[J]. 四川中医, 2017, 35(2): 57-59. HE Y J. The measurement of kaempferol-3-O-rutinoside from daphniphyllum calycinum using by HPLC[J]. Journal of Sichuan of Traditional Chinese Medicine, 2017, 35(2): 57-59. |
| [3] |
LUMMAETEE K, KU H M, WONGART W, et al. Optimization of supercritical fluid extraction of isoflavone from soybean meal[J]. Canadian Journal of Chemical Engineering, 2017, 95(6): 1141-1149. DOI:10.1002/cjce.22786 |
| [4] |
王学军, 许振良, 赵锁奇. 银杏叶提取物中槲皮素和芦丁的超临界流体色谱法测定[J]. 中国医药工业杂志, 2005, 36(7): 415-417. WANG X J, XU Z L, ZHAO S Q. Determination of quercetin and rutin in ginkgo biloba extractby supercritical fluid chromatography[J]. Chinese Journal of Pharmaceuticals, 2005, 36(7): 415-417. DOI:10.3969/j.issn.1001-8255.2005.07.014 |
| [5] |
WEST C, LEMASSON E. Unravelling the effects of mobile phase additives in supercritical fluid chromatography-Part Ⅱ:adsorption on the stationary phase[J]. Journal of Chromatography, 2019, 1593: 135-146. DOI:10.1016/j.chroma.2019.02.002 |
| [6] |
ROTH M. Thermodynamics of modifier effects in supercritical fluid chromatography[J]. The Journal of Physical Chemistry, 1996, 100(6): 2372-2375. DOI:10.1021/jp952450x |
| [7] |
何岩, 张敏华, 董秀芹. 常用夹带剂在超临界CO2中无限稀释扩散系数的MD计算[J]. 高校化学工程学报, 2008, 22(1): 152-156. HE Y, ZHANG M H, DONG X Q. Molecular dynamics simulation for calculating the diffusion coefficients of acetone, ethyl acetate and cyclohexane at infinite dilution solution of supercritical CO2[J]. Journal of Chemical Engineering of Chinese Universities, 2008, 22(1): 152-156. DOI:10.3321/j.issn:1003-9015.2008.01.028 |
| [8] |
YOO J H, BREITHOLZ A, IWAI Y, et al. Diffusion coefficients of supercritical carbon dioxide and its mixtures using molecular dynamic simulations[J]. Korean Journal of Chemical Engineering, 2012, 29(7): 935-940. DOI:10.1007/s11814-011-0248-5 |
| [9] |
WILKE C R, CHANG P. Correlation of diffusion coefficients in dilute solutions[J]. AIChE Journal, 1955, 1(2): 264-270. DOI:10.1002/aic.690010222 |
| [10] |
HE C H. Prediction of binary diffusion coefficients of solutes in supercritical solvents[J]. AIChE Journal, 1997, 43(11): 2944-2947. DOI:10.1002/aic.690431107 |
| [11] |
CHEN S H, DAVIS H T, EVANS D F. Tracer diffusion in polyatomic liquids. Ⅲ[J]. The Journal of Chemical Physics, 1982, 77(5): 2540. DOI:10.1063/1.444125 |
| [12] |
杨李慧.超临界二氧化碳在聚氨酯体系中溶解和扩散行为的分子动力学模拟研究[D].上海: 华东理工大学, 2017. YANG L H. Molecular dynamics simulation of the dissolution and diffusion of supercritical carbon dioxide in polyurethane systems[D]. Shanghai: East China University of Science and Technology, 2017. |
| [13] |
VAN ASSCHE T R C, BARON G V, DENAYER J F M. An explicit multicomponent adsorption isotherm model:Accounting for the size-effect for components with Langmuir adsorption behavior[J]. Adsorption, 2018, 24(6): 517-530. DOI:10.1007/s10450-018-9962-1 |
| [14] |
YEO S D, PARK S J, KIM J W, et al. Critical properties of carbon dioxide + methanol, + ethanol, +1-propanol, and +1-butanol[J]. Journal of Chemical & Engineering Data, 2000, 45(5): 932-935. |
| [15] |
董新艳.溶质在超临界CO2及含改性剂的超临界CO2中扩散系数及其构效关系研究[D].杭州: 浙江大学, 2012. DONG X Y. Diffusion coefficient in pure and modified supercritical CO2 and their structure-property relationship[D]. Hangzhou: Zhejiang University, 2012. |
| [16] |
曹秋瑾.香豆素及黄酮类物质在超临界CO2中的扩散系数研究[D].杭州: 浙江大学, 2016. CAO Q J. Study on the diffusion coefficient of coumarin and flavonoids in supercritical CO2[D]. Hangzhou: Zhejiang University, 2016. |
| [17] |
JABBARI M, GHARIB F. Solute-solvent interaction effects on protonation equilibrium of some water-insoluble flavonoids[J]. Journal of Solution Chemistry, 2011, 40(4): 561-574. DOI:10.1007/s10953-011-9667-5 |
| [18] |
SUAREZ J J, BUENO J L, Medina I. determination of binary diffusion coefficients of benzene and derivatives in supercritical carbon dioxide[J]. Chemical Engineering Science, 1993, 48(13): 2419-2427. DOI:10.1016/0009-2509(93)81063-2 |
| [19] |
LIONG K K, WELLS P A, FOSTER N R. Diffusion of fatty acid esters in supercritical carbon dioxide[J]. Industrial & Engineering Chemistry Research, 1992, 3l(1): 390-399. |
| [20] |
FUNAZUKURI T. Concerning the determination and predictive correlation of diffusion coefficients in supercritical fluids and their mixtures[J]. Journal of Supercritical Fluids, 2018, 134(SI): 28-32. |
| [21] |
朱虎刚, 田宜灵, 陈丽, 等. 超临界CO2+CH3OH及C2H5OH二元系的气液平衡[J]. 高等学校化学学报, 2002, 23(8): 1588-1591. ZHU H G, TIAN Y L, CHEN L, et al. Studies on vapor-liquid phase equilibria for SCF CO2+CH3OH and SCF CO2+C2H5OH systems[J]. Chemical Journal of Chinese Universities, 2002, 23(8): 1588-1591. DOI:10.3321/j.issn:0251-0790.2002.08.025 |
| [22] |
WELLS T, FOSTER N R, CHAPLIN R P. Diffusion of phenylacetic acid and vanillin in supercritical carbon dioxide[J]. Industrial & Engineering Chemistry Research, 1992, 31(3): 927-934. |
| [23] |
SILVA C M, FILHO C A, QUADRI M B, et al. Binary diffusion coefficients of α-pinene and β-pinene in supercritical carbon dioxide[J]. Journal of Supercritical Fluids, 2004, 32(1): 167-175. DOI:10.1016/j.supflu.2004.01.003 |
| [24] |
TING S S T, TOMASKO D L, FOSTER N R, et al. Solubility of naproxen in supercritical carbon dioxide with and without cosolvents[J]. Industrial & Engineering Chemistry Research, 1993, 32(7): 1471-1481. |
| [25] |
EKART M P, BENNET K L, EKART S M, et al. Cosolvent interactions in supercritical fluid solutions[J]. AIChE Journal, 1993, 39(2): 235-248. DOI:10.1002/aic.690390206 |
| [26] |
JANSSEN J G M, SCHOENMAKERS P J, CRAMERS C A. A fundamental study of the effects of modifiers in supercritical fluid chromatography[J]. Journal of Separation Science, 1989, 12(10): 645-651. |
| [27] |
POLING B E, PRAUSNITZ J M, O'CONNELL J P. The properties of gases and liquids[M]. 5th ed. New York: McGraw-Hill, 2001.
|
| [28] |
刘国杰, 贺网兴. 计算正常沸点下液体摩尔体积的基团贡献法[J]. 化学工程, 1990, 18(4): 62-65. LIU G J, HE W X. Group contribution method for calculating the molar volume of liquid at normal boiling point[J]. Chemical Engineering, 1990, 18(4): 62-65. |




