波形除雾器能有效分离气流中的雾滴,被广泛应用于化工、能源、海水淡化等工业领域[1-2]。其优点之一是压降低,有利于采用高气速以提高除雾器的处理能力,但不利之处是波折板表面聚集的雾滴会被气流二次夹带使捕集率随之下降[3],反而导致除雾器总体性能下降[4]。为了抑制二次夹带,一种方法是在波折板壁面安装排水钩[5],但除雾器压降会急剧增加,且使设备结构复杂,使用效果不佳[6]。另一种方法是波折板表面复合多孔泡沫层[7],减轻液体表面与气流的直接剪切作用,但液体在复杂多孔结构中传输阻力大,排液能力小,尤其在波折面水平放置、气液逆流工况下,雾滴二次夹带仍然不可避免。
由此可见,抑制二次夹带不仅要避免气液逆流,更重要的是及时移除捕集的雾沫、避免或降低其在壁面的聚集量。本研究采用内部输水性布料构建了波折面直立的气液错流波形除雾器(图 1(a)、(b)),除雾器壁面捕集到的液体在毛细力和重力联合作用下通过布料纤维内部传输、从底部排出,力图使壁面保持无液膜。目前除雾器壁面输水过程研究[7-9]尚未见气液错流下壁面内部输水的报道,有必要对此类除雾器内部输水性壁面二次夹带抑制机理、输水能力和除雾器负荷的预测模型进行系统的研究。
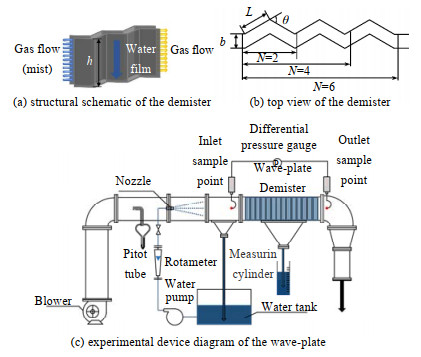
|
图 1 气液错流波形除雾器实验装置图 Fig.1 Schematic diagram of wave-plate demister with gas liquid cross-flow |
根据图 1(c)所示实验装置获取的雾沫捕集数据分析了该过程机理,建立了雾滴捕集率预测模型;结合布料输水性能参数测试,推导了内部输水性壁面膜厚预测关联式,结合二次夹带临界气速判定模型,与常规壁面除雾器对比绘制了气速-膜厚曲线图,定量表达了内部输水性壁面夹带抑制机理,并可为合理选择除雾器操作气速提供理论参考。
2 实验与模拟 2.1 雾滴捕集稳定工况下除雾器波形折板壁面捕集的雾滴量即为壁面内部输水量及外部降膜输水量的总和。为获得雾滴捕集率与壁面降膜膜厚之间的定量关系,首先需要根据雾滴捕集率实验数据建立雾滴捕集率预测模型。
2.1.1 雾滴捕集实验研究本研究设计的气液错流波形除雾器实验装置及其几何结构如图 1所示。表 1中列出其详细几何参数。实验过程中,鼓风机提供0.5~1.0 kPa(表压)的循环空气经计量后进入喷雾段,携带喷雾器产生的细雾滴通过混合段均化,进入波形除雾器之前在入口测量段用马尔文帕纳科Spraytec喷雾粒度仪对气流中的雾滴进行表征,其粒径分布如图 2所示,入口雾滴的粒径dp在1~30 μm,索特平均直径D3, 2为7.04 μm。在除雾器迎流面用等动力学采样管[10]将含雾气流引入装有200 mL纯水的洗气瓶中,雾滴(浓度为0.01 mol⋅L−1的KCl稀溶液)带入的电解质增量Δme与洗气瓶内液体电导率变化量Δσ满足标定的线性关系。实验在20 ℃下进行,采用同批配制的KCl稀溶液喷雾,并使用等动力学采样管、等容量采样方法。该除雾器共有120级波折板,每间隔10级波折板设置采样点,通过测量洗气瓶中电导率变化量即可从标定曲线得到该次采样气流中的雾滴质量分数。根据所测进口和出口处雾滴质量分数win和wout,通过下式计算除雾器雾滴平均质量捕集率:
|
|
表 1 波形除雾器结构尺寸 Table 1 Structural parameters of the demister |
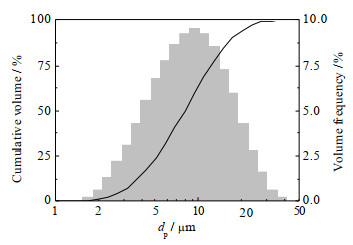
|
图 2 除雾器入口雾滴的粒径分布 Fig.2 Diameter distribution of droplets entering into demister |
| $\eta = \frac{{{w_{{\rm{in}}}} - {w_{{\rm{out}}}}}}{{{w_{{\rm{in}}}}\;}} \times 100\;{\rm{\% }}$ | (1) |
电导率测量法获得的是除雾器总的质量捕集率,作为一种验证手段,借助图 2所示粒径分布数据通过加权平均,可以检验数值模拟方法获得的不同粒径雾滴的粒级捕集率,这对除雾器性能表征具有重要意义。模拟基于以下合理化假设[11-13]:
(1) 除雾器通道由多个等间距的单通道并行排列而得,通道高度远大于通道间距与波折长度,因此将三维多通道多相流简化成二维单通道;
(2) 实验中气流Mach数远小于0.1,视为不可压缩流;
(3) 雾滴被视为球形液滴,只受流体曳力作用,且忽略液滴之间碰撞;
(4) 液滴接触壁面即认为捕集,不考虑液滴破碎及溅射造成的夹带影响。
使用ICEM CFD创建二维几何模型,对10级波折板(N=10)的除雾通道进行结构化网格划分,并对近壁面附近区域利用边界层网格进行加密处理。网格划分完毕后导入Fluent 2019 R2进行数值计算。在模拟中,气相流场基于欧拉法求解,由于其流动为湍流,采用了Realizable k-ε湍流模型[10, 19]进行求解,用SIMPLE算法求解控制方程,并采用二阶迎风法将气体流动方程离散化。各变量的收敛标准设置为10−5。液滴轨迹则基于拉格朗日法进行计算,采用DPM(discrete phase model)模型模拟液滴运动。
根据被捕集的单一粒径雾滴质量流量qm, d, t与其进口质量流量qm, d, i之比,即可确定该粒径雾滴模拟捕集率:
| $ {\eta _{\text{d}}} = \frac{{{q_m}{{_, }_{{\text{d, t}}}}}}{{{q_{m, }}_{{\text{d, i}}}}} $ | (2) |
内部输水性能直接影响被捕集雾滴在布料壁面上的传输和成膜,由此影响捕集壁面的降膜及雾沫夹带。为研究不同布料的内部输水性能,设计了图 3所示的布料内部输水速率测量实验,采用长宽为30 cm×10 cm的3种布料(苎麻布料、亚麻布料、棉布料)在室温下进行实验。
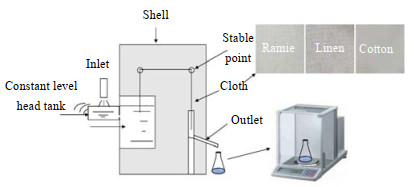
|
图 3 布料内部输水实验装置图 Fig.3 Schematic diagram of the experimental device for liquid transport in cloth |
实验中,水槽水位由外置恒液位槽控制,布料一端浸入水槽中,液体在毛细力与重力联合作用下于布料内部传输,在布料另一端汇聚成液滴滴落到锥形瓶中并由电子天平称量。在实验过程中(0 ~ 3.5 h),布料表面未观察到液膜存在,表明液体转移全部通过布料内部传输完成。根据所测宽度为w的布料在不同时间段Δt内传输液滴质量Δm,可计算出单位宽度布料内部的输水速率vΔt:
| $ {v_{\Delta t}} = \frac{{\Delta m}}{{\Delta t \cdot w}} $ | (3) |
图 4为波折板级数N=10时粒级捕集率随气速的变化。可以看出,随气速增大,雾滴惯性越大,捕集率增大;粒径增大也使捕集率上升,当粒径达到20 μm时,雾滴接近全捕集,这是因为粒径越大的雾滴惯性越大,越不容易随气流方向改变运动方向,越容易被捕集。
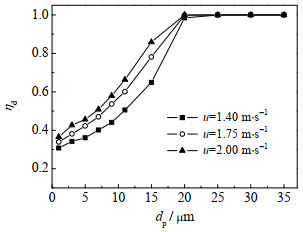
|
图 4 N =10时捕集率随气速的变化 Fig.4 Grade efficiency as a function of gas velocity at N=10 |
波形除雾器为多级波折板的串联结构,Jackson等[14-16]认为,每级波折板对同一粒径的雾滴捕集率ηd, b均相等。因此除雾器单一粒径捕集率ηd, t随级板数变化的计算式为
| $ {\eta _{{\text{d, t}}}}{\text{ = 1}} - {{\text{(1}} - {\eta _{{\text{d, b}}}})^N} $ | (4) |
模拟结果为单一粒径雾滴的捕集率,试验中利用马尔文激光粒度测量仪可得到某一粒径雾滴的体积分数(见图 2)。由于雾滴密度为常数,其质量分数wd等于其体积分数,采用权重加和方式,计算已知雾滴粒径分布的总质量捕集率:
| $ \eta {\text{ = }}\frac{{\sum\nolimits_{{d_1}}^{{d_{\text{n}}}} {\left( {{w_{\text{d}}}{\eta _{{\text{d, t}}}}} \right)} }}{{\sum\nolimits_{{d_1}}^{{d_{\text{n}}}} {{w_{\text{d}}}} }} $ | (5) |
该模拟计算加权统计值与实验结果具有同一基准下对比意义。
图 5为不同气速下除雾器捕集率的实验值和模拟值的对比图,结果表明:在不同工况下,模拟值和实验值符合良好,相对误差均小于13.7%,说明本研究采用的计算模型可以较好地反映雾滴捕集情况。由图可见,增加气流速度u和波折板级数N均可提高除雾器捕集率。
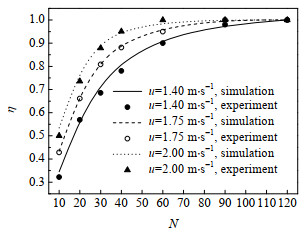
|
图 5 实验数据和模拟数据对比图 Fig.5 Comparison of simulated separation efficiency and experimental results |
如前所述以单位时间、单位布料宽度的输水速率vΔt表示布料内部输水性能,3种布料在0 ~ 3.5 h内单位宽度输水质量累计值q的实验检测结果如图 6所示。由图 6可见,干布料接触纯水初期,布料处于液体润湿扩散过程,前15 min输水量为0;随着传输时间延长,布料内部输水通道越来越通畅,输水量持续增加,输水量曲线斜率在45 min后基本保持恒定,输水质量与传输时间呈线性关系,说明形成内部输水通路后,输水速率vΔt即保持稳定。由此可见,对于内部输水性布料,在除雾器长期稳态工况下,在不含堵塞性杂质的雾滴捕集过程中,布料内部液体传输速率vΔt为恒定值,因此本研究设定传输稳定后的输水速率即为该布料的内部输水速率vΔt。
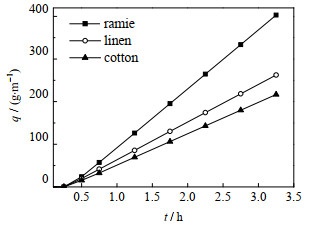
|
图 6 布料的内部输水质量随时间的变化 Fig.6 Water transported in cloth as a function of time |
研究选择了3种实验材料中内部输水速率最大的苎麻布料为除雾器装置内部的雾滴捕集壁面材料,其vΔt =3.84×10−5 kg⋅(m⋅s)−1。
4 输水过程及夹带抑制机理分析 4.1 捕集模型的建立除雾器壁面输水过程将影响雾沫夹带,而其壁面内部及外部传输的液体来自雾滴的捕集,二者互为因果,从机理分析角度更需要建立显式的雾滴捕集率计算模型。经典的Burkholz[17]雾滴捕集理论将粒径dp与气流速度u这2个关键参数归纳为液滴斯托克斯数St,单级波折板雾滴捕集率ηd, b是St和波折板偏转角θ的乘积:
| $ St = \frac{{{\rho _{\text{d}}}u{d_{\text{p}}}^2}}{{18{\mu _\rm{g}}b}} $ | (6) |
式中:ρd为雾滴密度,kg⋅m−3;μg为气体黏度,Pa⋅s。
| $ {\eta _{{\text{d, b}}}} = St \cdot \theta $ | (7) |
但该模型未考虑湍流下液滴颗粒的混合,其对大的斯托克斯数范围预测偏差较大,本研究借鉴Wikinson模型[18],引入湍流影响修正因子fc,并利用前述模拟结果获得fc的拟合表达式fc=2.718×(4.4461St2+1)−0.6,由此得到新的单级波折雾滴捕集率预测模型:
| $ {\eta _{{\text{d, b}}}}{\text{ = }}St \cdot \theta \cdot {f_{\text{c}}} $ | (8) |
该模型可计算不同气速下不同粒径的雾滴捕集率,为方便后续代入输水模型且不失代表性,借鉴文献[8]的做法,以雾滴粒径范围对应的索特平均粒径D3, 2代入式(8)计算得到的捕集率代表按粒径分布加权平均值,与本研究实验结果对比,其误差在±20% 以内,这说明在本实验条件下,采用该简化模型进行壁面输水过程机理分析是合理的。
4.2 输水及夹带模型对于常规除雾器,随着雾滴不断被捕集,液滴或汇聚形成局部液膜沿壁面下降;或汇聚形成较大液滴,悬挂在壁面上,直到超过临界厚度后开始滑落[19],故输水过程中壁面液膜厚度不均匀,如图 7(a)所示。而内部输水性壁面由于其材料可浸润,被捕集的雾滴可立即被壁面吸收并铺展,若形成液膜也会是均匀的,如图 7(b)所示。
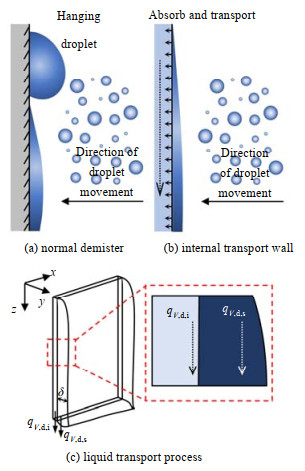
|
图 7 雾滴在不同壁面的输水过程示意图 Fig.7 Schematic diagram of liquid transport on different walls |
基于雾滴捕集率计算模型式(8),被捕集雾滴汇聚的体积流量(m3⋅s−1):
| $ {q_{V{\text{, t}}}} = \frac{{u \cdot h \cdot b \cdot {c_{{\text{in}}}} \cdot {\eta _{{\text{d, b}}}}}}{{{\rho _{\text{d}}}}} $ | (9) |
式中:b为板间距,m;h为板高,m;cin为入口气流中雾滴质量浓度,kg⋅m−3;雾滴捕集率为粒径D3, 2的代表值。
稳定工况下除雾器波形折板壁面捕集的雾滴量qV, t为壁面内部输水量qV, d, i(m3⋅s−1)及外部降膜输水量qV, d, s(m3⋅s−1)的总和:
| $ {q_{V{\text{, t}}}} = {q_{V{\text{, d, i}}}} + {q_{V{\text{, d, s}}}} $ | (10) |
基于内部输水性能实验测得的布料内部输水速率vΔt,水平长度L的壁面内部输水体积流量qV, d, i为
| $ {q}_{V\text{, }}{}_{\text{d, i}}=\frac{{v}_{\Delta t}\cdot L}{{\rho }_{\text{d}}} $ | (11) |
根据Nusselt液膜理论,壁面液膜厚度δ与壁面降膜输水量qV, d, s的关系为:
| $ {q_{V{\text{, }}}}_{{\text{d, s}}} = \frac{{{\rho _{\text{d}}}g}}{{3{\mu _{\text{l}}}}}{\delta ^3}L $ | (12) |
式中:g为重力加速度,m⋅s−2。联立式(9)~(12),得到内部输水性壁面波形除雾器液膜厚度δ关联式:
| $ \delta = {\left( {\frac{{3{\mu _\rm{l}}}}{{{\rho _{\text{d}}}^2g}}} \right)^{1/3}}{\left( {u \cdot \frac{h}{L} \cdot b \cdot {c_{{\text{in}}}} \cdot {\eta _{{\text{d, b}}}} - {v_{\Delta \rm{t}}}} \right)^{1/3}} $ | (13) |
根据Wang等[20]夹带临界判定模型得到夹带临界气速ugc与液膜厚度δ的关系:
| $ {u_{{\text{gc}}}} = {1.655_{}}4{\left( {\frac{{{\mu _\rm{l}}^2{\sigma _\rm{l}}}}{{{\mu _{\text{g}}}{\rho _{\text{g}}}{\rho _{\text{d}}}}}} \right)^{1/3}}{\left( {b\cos \theta } \right)^{1/3}}{\left| {\frac{1}{{\left( {R + \delta } \right)\left( {\frac{1}{2}{\delta ^2} - \delta R + {R^2} \cdot \ln \frac{{R + \delta }}{R}} \right)}}} \right|^{1/3}} $ | (14) |
式中:R为波折板弯折处的曲率半径,m。
结合式(13)、(14)得到,壁面材料内部输水能力越强,壁面液膜厚度越薄,故发生夹带时的临界气速越高。
对于常规除雾器壁面,悬挂液滴处的局部膜厚大于降膜区域平均膜厚,更容易被气流剪切。液体与壁面之间的液固接触角越大,越易形成液滴悬挂,悬挂的液滴汇聚增大至脱落直径后沿壁面滑落。闵敬春等[21]研究了竖直平壁上液滴沿壁面下滑时的液滴临界厚度δc(m),可由式(15)得到
| $ {\delta _{\text{c}}} = {\left\{ {\frac{{6{\sigma _\rm{l}}}}{{{\rho _{\text{d}}}g}}\frac{{\frac{{\sin {\theta _{\text{A}}} + \sin {\theta _{\text{R}}}}}{{\pi - \left( {{\theta _{\text{A}}} - {\theta _{\text{R}}}} \right)}} - \frac{{\sin {\theta _{\text{A}}} + \sin {\theta _{\text{R}}}}}{{\pi + \left( {{\theta _{\text{A}}} - {\theta _{\text{R}}}} \right)}}}}{{3 + {{\left( {\rm{tg}\frac{{{\theta _{\text{A}}} + {\theta _{\text{R}}}}}{4}} \right)}^2}}}\rm{tg}\left( {\frac{{{\theta _{\text{A}}} + {\theta _{\text{R}}}}}{4}} \right)} \right\}^{1/2}} $ | (15) |
式中:σl为液滴表面张力,N⋅m−1;θA和θR分别为前进和后退接触角,rad。
根据式(13)~(15),绘制出不同壁面的液膜厚度δ与气速u的关系图,如图 8所示。图中a线为内部输水性壁面上的液膜厚度,其液膜为完全铺展状态;b线为假设液膜在常规非浸润壁面上为完全铺展状态时的膜厚。c线为悬挂液滴脱落临界厚度,d线为夹带临界线,e线为壁面悬挂液滴被夹带临界线。
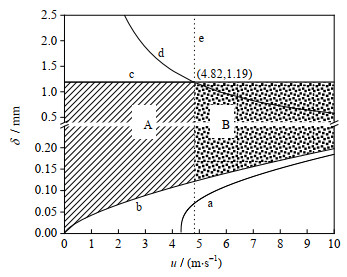
|
图 8 除雾器膜厚与气速关系图 Fig.8 Relationship between film thickness and gas velocity |
在实际除雾过程中,雾滴在常规除雾器壁面上为液滴、液膜共存状态,即液膜厚度处于b、c线之间的A、B区域。在区域A内,其壁面上液膜和悬挂液滴的厚度均小于临界值,因此在区域A内不会发生夹带;当气速超过夹带临界气速(图中为4.82 m⋅s−1)时,气流的剪切力与壁面上悬挂液滴的黏性力无法平衡,此时在B区域内发生夹带,图中表现为d线(夹带临界线)穿越了B区域。
对于内部输水性壁面除雾器,当气速不超过降膜临界气速(图中为4.35 m⋅s−1)时,雾滴捕集量不会大于其壁面内部输水量,其壁面液膜厚度为0,完全不会发生夹带。气速超过降膜临界气速后,壁面开始出现降膜,随着气速增加,雾滴捕集量增加,壁面液膜厚度随之增加,气速超过夹带临界气速(理论计算值为19.52 m⋅s−1)后,才会产生夹带。相比于常规除雾器,苎麻布料的内部输水性能使液膜在捕集壁面上均匀铺展,故其壁面液膜厚度更薄,非夹带区域更大。
5 结论(1) 雾滴捕集实验结果表明,采用提高气速、增加级数的措施可有效提高雾滴捕集率;基于惯性分离机理,建立了用于雾滴捕集率预测的半经验模型,模型计算值与实验值相比,误差在±20% 之内,能较好地预测不同工况下的雾滴捕集率。
(2) 通过对内部输水性波形除雾器壁面的输水过程进行分析,建立了膜厚预测关联式:不同内部输水性材料在稳定输水过程中具有不同的内部输水速率,壁面材料内部输水能力越强,壁面降膜厚度越薄。
(3) 内部输水壁面能有效降低液膜厚度,且液滴能在壁面完全铺展,从而抑制夹带发生。模型计算显示,常规除雾器当气速超过夹带临界气速4.82 m⋅s−1时即可能产生液沫夹带,而内部输水性壁面除雾器在气速4.35 m⋅s−1时尚处于无液膜状态,其临界夹带气速提高到19.52 m⋅s−1,可显著强化除雾器处理能力。
| [1] |
MAO F, TIAN R, CHEN Y, et al. Re-entrainment in and optimization of a vane mist eliminator[J]. Annals of Nuclear Energy, 2018, 120: 656-665. DOI:10.1016/j.anucene.2018.06.011 |
| [2] |
VENKATESAN G, KULASEKHARAN N, MUTHUKUMAR V, et al. Regression analysis of a curved vane demister with Taguchi based optimization[J]. Desalination, 2015, 370: 33-43. DOI:10.1016/j.desal.2015.05.011 |
| [3] |
SONG J, HU X. A mathematical model to calculate the separation efficiency of streamlined plate gas-liquid separator[J]. Separation and Purification Technology, 2017, 178: 242-252. DOI:10.1016/j.seppur.2017.01.044 |
| [4] |
AZZOPARDI B J, SANAULLAH K S. Re-entrainment in wave-plate mist eliminators[J]. Chemical Engineering Science, 2002, 57(17): 3557-3563. DOI:10.1016/S0009-2509(02)00270-1 |
| [5] |
GALLETTI C, BRUNAZZI E, TOGNOTTI L. A numerical model for gas flow and droplet motion in wave-plate mist eliminators with drainage channels[J]. Chemical Engineering Science, 2008, 63(23): 5639-5652. DOI:10.1016/j.ces.2008.08.013 |
| [6] |
KAVOUSI F, BEHJAT Y, SHAHHOSSEINI S. Optimal design of drainage channel geometry parameters in vane demister liquid–gas separators[J]. Chemical Engineering Research and Design, 2013, 91(7): 1212-1222. DOI:10.1016/j.cherd.2013.01.012 |
| [7] |
XU Y, YANG Z, ZHANG J. Study on performance of wave-plate mist eliminator with porous foam layer as enhanced structure. Part Ⅱ: Experiments[J]. Chemical Engineering Science, 2017, 171: 662-671. DOI:10.1016/j.ces.2017.05.030 |
| [8] |
XU J, HRNJAK P. Impinging oil separator for compressors[J]. International Journal of Refrigeration, 2020, 119: 110-118. DOI:10.1016/j.ijrefrig.2020.07.013 |
| [9] |
RUIZ J, CUTILLAS C G, KAISER A S, et al. Experimental study on pressure loss and collection efficiency of drift eliminators[J]. Applied Thermal Engineering, 2018, 149: 94-104. |
| [10] |
废气低浓度颗粒物采样常见问题的梳理[J]. 环境与发展, 2020, 32(5): 126-127. ZHANG W, WU X Y, LI R. Combating common problems in sampling low concentration particulates of exhaust gas[J]. Environment and Development, 2020, 32(5): 126-127. |
| [11] |
除雾器内雾滴运动特性与除雾效率[J]. 化工学报, 2014, 65(12): 4669-4677. HAO Y J, LIU J Y, YUAN Z L, et al. Movement characteristics of droplets and demisting efficiency of mist eliminator[J]. CIESC Journal, 2014, 65(12): 4669-4677. |
| [12] |
折线型与流线型除雾器性能的数值模拟与分析[J]. 中氮肥, 2013(1): 34-35. LIN Q C, LIU X, ZHOU X, et al. Numerical simulation on performances of droplet eliminator[J]. M-Sized Nitrogenous Fertilizer Progress, 2013(1): 34-35. DOI:10.3969/j.issn.1004-9932.2013.01.014 |
| [13] |
LIU Y, QU Z. Numerical investigation of moisture separators with corrugated plates[J]. Energy Procedia, 2017, 105: 1501-1506. DOI:10.1016/j.egypro.2017.03.450 |
| [14] |
JACKSON S, CALVERT S. Entrained particle collection in packed beds[J]. AIChE Journal, 1966, 12(6): 1075-1078. DOI:10.1002/aic.690120608 |
| [15] |
GUAN L, YUAN Z, YANG L, et al. Numerical study on the penetration of droplets in a zigzag demister[J]. Environmental Engineering Science, 2016, 33: 35-43. DOI:10.1089/ees.2014.0367 |
| [16] |
WANG Y I, JAMES P W. The calculation of wave-plate demister efficiencies using numerical simulation of the flow field and droplet motion[J]. Chemical Engineering Research and Design, 1998, 76(8): 980-985. DOI:10.1205/026387698525630 |
| [17] |
BÜRKHOLZ A. Droplet separation [M]. New York: VCH Publishers, 1989.
|
| [18] |
WILKINSON D. Optimizing the design of waveplates for gas-liquid separation[J]. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 1999, 213(4): 265-274. DOI:10.1243/0954408991529870 |
| [19] |
KIM S W, KIM J, PARK S S, et al. Enhanced water collection of bio-inspired functional surfaces in high-speed flow for high performance demister[J]. Desalination, 2020, 479: 114314. DOI:10.1016/j.desal.2020.114314 |
| [20] |
WANG B, TIAN R. Investigation on flow and breakdown characteristics of water film on vertical corrugated plate wall[J]. Annals of Nuclear Energy, 2019, 127: 120-129. DOI:10.1016/j.anucene.2018.12.001 |
| [21] |
竖壁上液滴的脱落直径[J]. 应用基础与工程科学学报, 2002, 10(1): 57-62. MIN J C, PENG X F, WANG X D. Departure diameter of a drop on a vertical plate[J]. Journal of Basic Science and Engineering, 2002, 10(1): 57-62. DOI:10.3969/j.issn.1005-0930.2002.01.008 |




