2. 国家压力容器与管道安全工程技术研究中心, 安徽 合肥 230031
2. National Technology Research Center for Safety Engineering of Pressure Vessels and Pipelines, Hefei 230031, China
电脱盐是原油与含盐水分离的过程[1],利用电脱盐降低原油中盐的质量浓度,可以预防和控制下游设备腐蚀。电脱盐是一个复杂的多因素耦合系统,受多种因素影响,如原油温度、盐的质量浓度及脱盐罐界位等[2, 3],工艺操作参数对脱盐效率具有重要影响[3-6]。
传统的有关电脱盐系统影响因素及其影响规律研究方法,主要从探究因果关系出发,提出了很多定性或定量结论[3]。但受限于系统的复杂性,机理模型往往难以精确构建,且机理模型往往只在一定范围内发挥作用[7-8]。基于机理的方法通常通过简化试验条件、忽略次要因素等方法开展研究,选择典型关键因素,如原油温度、混合压差等开展研究[3],但由于原油种类、脱盐工艺、破乳剂类型、操作参数不同,研究结论的普适性以及研究结果用于指导实际操作还存在较多问题[5]。
大数据方法对全部样本数据开展分析以探究数据背后的规律,可以克服机理模型的不足,因而在工程中获得广泛应用,如复杂系统中目标函数与影响因素的相互关系分析[9-12],系统能效、生产效率优化分析[13-15],化学反应分析、场景优化等[16-18]。
本研究通过获取对电脱盐有影响的因素,采用分类方法建立影响因素与脱盐效果的大数据模型,提出影响因素的关键性分析方法,在此基础上提出基于线性规划的优化技术,该方法在脱盐过程关键影响因素分析、脱盐效果智能监测、电脱盐操作参数优化中得到验证。
2 基于大数据的电脱盐质量浓度智能监测与优化模型 2.1 机理模型与大数据模型传统的机理模型研究影响因素多元、耦合关系复杂的系统,往往需要借助大量的先验经验和试验。如开展多种失效机制作用下的主导失效模式分析时,寻找主导影响因素就变得十分关键[19]。通过正交试验、主元分析等方法,结合机理分析在一定程度上可以弥补机理模型的不足[20]。
大数据模型通过获取与现象相关的全部数据,采用数据分析研究背后的规律。该方法随着近年来传感技术、数据科学的发展应运而生并快速发展[21-22]。流程行业自动化程度高、测点丰富,数据获取具备天然条件,这为大数据技术应用提供了数据基础[23-24]。以电脱盐系统为例,在长期运行中分布式控制系统(distributed control system,DCS)、实验室信息管理系统(laboratory information management system, LIMS)等记录了大量数据。充分利用这些数据,建立影响因素与脱盐效果的定量关系模型,既可用于脱盐效果的实时监测,又可用于影响因素定量分析与优化,这是传统方法所不具备的。
2.2 基于大数据的电脱盐装置智能监测模型基于大数据的脱盐效果智能监测模型主要通过获取影响脱盐后盐的质量浓度的全部因素,建立影响因素与脱盐后盐的质量浓度的映射关系模型,并利用模型开展智能预测与优化分析。
假设某电脱盐工艺过程受多因素共同作用,第
| $ f\left( {{\boldsymbol{X}_i}} \right) \to {y_i} $ | (1) |
将大数据方法应用于电脱盐系统的优化分析时,必须依据电脱盐装置的实际情况,做出合理的判断,如考虑样本的数量与影响因素数量,影响因素之间的非线性,以及模型应用中可能存在的欠拟合及过拟合等。本研究采用多维高斯贝叶斯算法建立脱盐后盐的质量浓度智能监测模型:
| $ P\left(\boldsymbol{X} \mid C_k\right)=\frac{1}{\sqrt{(2 {\rm{\mathit{π}}})^N\left|\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k\right|}} \exp \left(-\frac{1}{2}\left[\boldsymbol{X}-\boldsymbol{\mu}_k\right]^{\mathrm{T}} \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k^{-1}\left[\boldsymbol{X}-\boldsymbol{\mu}_k\right]\right) $ | (2) |
式中:通过从DCS获取电脱盐操作参数,将参数代入不同盐的质量浓度分类的模型中,联合分布概率密度最大的即为最可能的分类,这样就可以利用模型对盐的质量浓度进行在线监测。
从2.2节模型可以发现,某一工况
| $ L = \ln \left( {P\left( {\left. \boldsymbol{X}\right|{C_k}} \right)} \right) = - \frac{1}{2}\left[ {\ln \left( {\left| {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k}} \right|} \right) + {{[\boldsymbol{X} - {\boldsymbol{\mu}_k}]}^T}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k^{ - 1}[\boldsymbol{X} - {\boldsymbol{\mu}_k}] + N\ln \left( {2{\rm{\mathit{π}}} } \right)} \right] $ | (3) |
由于特定分类的协方差矩阵行列式
| $ \frac{{\partial L}}{{\partial {x_i}}} = - \frac{1}{2}\frac{{\partial {{\left[ {\boldsymbol{X} - {\boldsymbol{\mu}_k}} \right]}^T}}}{{\partial {x_i}}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k^{ - 1}\left[ {\boldsymbol{X} - {\boldsymbol{\mu}_k}} \right] - \frac{1}{2}{\left[ {\boldsymbol{X} - {\boldsymbol{\mu}_k}} \right]^T}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k^{ - 1}\frac{{\partial \left[ {\boldsymbol{X} - {\boldsymbol{\mu}_k}} \right]}}{{\partial {x_i}}} $ | (4) |
式中:当
式(4)实质是求概率密度对影响因素的偏导数,偏导数数值反映了因素对概率密度的影响程度,符号反映了因素对概率密度变化的影响方向。若将多因素简化到单一因素,则多维高斯贝叶斯模型的概率密度转化为经典的单因素高斯分布,如图 1所示。
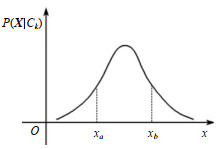
|
图 1 一维高斯分布的概率密度模型 Fig.1 Probability density profile of the univariate Gaussian distribution model |
电脱盐装置中部分因素具有一定耦合关系(如脱盐罐原油出口温度受进口温度影响),为减少冗余影响,通常希望影响因素
本研究采用主成分分析(principal component analysis, PCA)方法计算线性无关的影响因素。若影响脱盐后盐的质量浓度的
| $ \boldsymbol{X}= \boldsymbol{A} \cdot [\boldsymbol{E} - {\boldsymbol{\mu}_{\bf{E}}}] $ | (5) |
式中:
式(4)给出了提高工况X隶属于
利用式(5)计算时,当
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\min \left( {{k_1} \cdot x_{i1}^\prime = {k_1} \cdot \mathit{\boldsymbol{A}} \cdot \left[ {\mathit{\boldsymbol{E}} - {\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{E}}}} \right]} \right)\quad \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\rm{ 当 }}\frac{{\partial L}}{{\partial {x_{i1}}}} > 0{\rm{ 时 }}{k_1} = - 1{\rm{, 当 }}\frac{{\partial L}}{{\partial {x_{i1}}}} < 0{\rm{ 时}}{k_1} = 1} \right)\\ {\rm{ s}}{\rm{.t}}{\rm{. }}\left\{ {\begin{array}{*{20}{c}} {{k_2} \cdot x_{i2}^\prime = {k_2} \cdot \mathit{\boldsymbol{A}} \cdot \left[ {\mathit{\boldsymbol{E}} - {\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{E}}}} \right] \le {k_2} \cdot {x_{i2}}}&{\left( {{\rm{ 当 }}\frac{{\partial L}}{{\partial {x_{i2}}}} > 0{\rm{ 时 }}{k_2} = - 1,\quad {\rm{当}}\frac{{\partial L}}{{\partial {x_{i2}}}} < 0{\rm{ 时 }}{k_2} = 1} \right)}\\ \vdots & \vdots \\ {{k_N} \cdot x_{iN}^\prime = {k_N} \cdot \mathit{\boldsymbol{A}} \cdot \left[ {\mathit{\boldsymbol{E}} - {\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{E}}}} \right] \le {k_N} \cdot {x_{iN}}\quad }&{\left( {{\rm{ 当}}\frac{{\partial L}}{{\partial {x_{iN}}}} > 0{\rm{ 时 }}{k_N} = - 1,\quad {\rm{当}}\frac{{\partial L}}{{\partial {x_{iN}}}} < 0{\rm{ 时 }}{k_N} = 1} \right)} \end{array}} \right. \end{array} $ | (6) |
式中:
依据2.2~2.4节所述的方法,可以构建基于大数据的电脱盐系统智能监测与优化流程,如图 2所示。
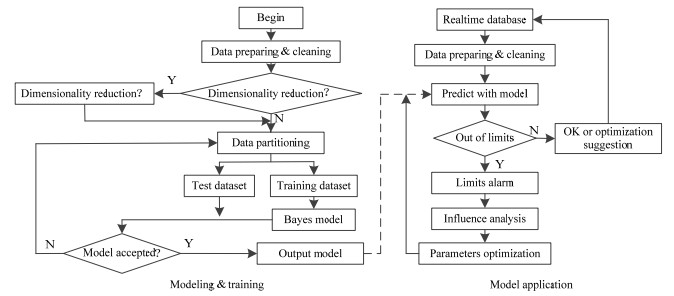
|
图 2 基于大数据的电脱盐系统智能监测与优化流程图 Fig.2 Flow chart of intelligent monitoring and optimization processes for the electro-desalting system based on big data |
某石化企业电脱盐系统脱盐后盐的质量浓度的大数据模型选取了脱盐罐操作参数、各类注剂、原料组成及电场强度等40个参数作为影响因素,各因素的内容见表 1。
|
|
表 1 电脱盐系统大数据分析模型主要影响因素 Table 1 Main parameters in the big data analysis model for the electro-desalting system |
为验证模型的准确性,以召回率为指标对全部样本进行了验证。召回率指模型预测得到的脱盐后盐的质量浓度高于某阈值的工况数量在全部超过该阈值的工况数中的占比。验证结果如图 3、4所示。
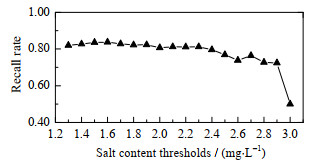
|
图 3 不同脱盐后盐的质量浓度控制值的召回率 Fig.3 Recall rate profile of over-threshold samples |
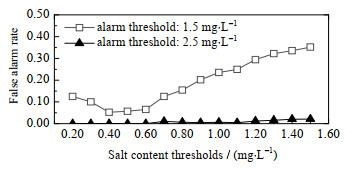
|
图 4 不同报警阈值的误报率 Fig.4 False alarm rate profiles under different alarm thresholds |
图 3中横坐标为脱盐后盐的质量浓度控制指标,纵坐标为召回率,当控制值为1.5 mg⋅L−1时,正确识别出584个超标工况中的488个,识别率为0.84。随着控制阈值增加,识别率有所下降,通过增加样本数量可对该问题进行弥补。大多数情况下,召回率可以保持在0.80以上。图 4为不同报警阈值时的误报率,当报警阈值为1.5 mg⋅L−1时,多数实际盐的质量浓度低于1 mg⋅L−1的工况被误判为超标,误报率在0.25以下。而当报警阈值定为2.5 mg⋅L−1时,误报率始终维持在很低的数值,显示模型具有较好的防误报功能。
考察全部近1 300个样本中不同工况的召回率,分类统计结果如表 2所示。表中,ρ为脱盐后盐的质量浓度,以1.5 mg⋅L−1为阈值进行优化分析可以发现,89.6% 的脱盐后盐的质量浓度范围在1.5~2.0的工况可以被正确识别,接近84.4%的脱盐后盐的质量浓度范围为2.0~3.0的工况可以被正确识别,盐的质量浓度为3.0以上的召回率为70.0%。识别这些脱盐效果不佳的工况,可为电脱盐的运行优化提供依据。
|
|
表 2 阈值为1.5 mg⋅L−1时不同脱盐后盐的质量浓度的工况召回率 Table 2 Recall rates of samples with different after-desalination salt contents (threshold = 1.5 mg⋅L−1) |
以脱盐后盐的质量浓度为1.5 mg⋅L−1为控制阈值,对948个异常工况进行优化,优化时最多选择3个参数。结果表明,只有5个工况无法达到1.5 mg⋅L−1的优化目标。依据关键影响因素出现的频次排列,依次筛选出电脱盐的关键影响因素并统计其与优化参数的偏离情况,结果如表 3所示。
|
|
表 3 2019.5~2021.1间电脱盐关键影响因素、偏离情况及相关性 Table 3 Key parameters, deviations and correlations of the electro-desalting system from 2019.5 to 2021.1 |
从表中可见,2019.5~2021.1期间,对电脱盐影响最大的是二级电脱盐罐界位,约占待优化工况的62.3%,一级脱盐罐出口温度次之,一级脱盐罐界位影响第三,占35.7%。从调整方向看,82.9% 的二级脱盐罐和37.9% 的一级脱盐罐界位过低。82.4% 的二级脱盐罐入口混合压差过高。此外,一级脱盐罐入口温度过低、二级脱盐罐出口温度过低和一级脱盐罐入口混合压差过高对脱盐效果具有负面影响。
采用相关分析法对影响因素灵敏性进行了分析,除因素7、8外,按顺序各因素的相关性绝对值总体逐渐减小。由于因素7、8与2高度相关,因素2调整时,会同步影响因素7、8,故因素7、8也对脱盐效果表现出较强的相关性。
2019.5~2021.1期间电脱盐系统影响因素关键性排列如下:二级脱盐罐界位 > 一级脱盐罐出口温度 > 一级脱盐罐界位 > 二级脱盐罐入口混合压差 > 一级脱盐罐入口注水量 > 二级脱盐罐脱硫净化水流量 > 一级脱盐罐原油温度 > 二级脱盐罐出口温度 > 一级脱盐罐入口混合压差。关键性排序可能会随着工况调整发生变化。
4.2 部分影响因素分析 4.2.1 脱盐罐界位的影响脱盐罐界位的影响如图 5所示。在全部涉及二级脱盐罐界位调整的工况中,591个界位过低的工况数据范围为22.03%~31.45%,均值为26.36%,101个界位过高的工况数据范围为28.39%~47.40%,均值为40.97%。基于此,建议二级脱盐罐界位控制在26.36%~40.97%,一级脱盐罐界位建议控制在30.33%~45.13%。由于脱盐罐界位不是决定脱盐效果的唯一因素,因而合理的界位还应考虑其他因素的影响。
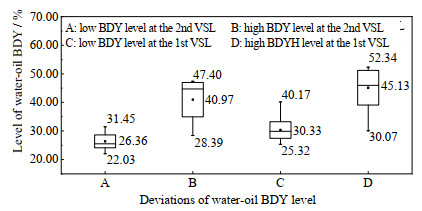
|
图 5 一、二级脱盐罐界位偏离情况比较 Fig.5 Comparison of water-oil boundary (BDY) level deviations at 1st and 2nd electro-desalting vessels |
脱盐罐混合压差的影响如图 6所示。分析表明,该电脱盐装置二级混合压差严重偏高,约32.3%的优化工况涉及二级混合压差调整,其中偏高的占82.4%,范围为87.95~125.93 kPa。二级混合压差偏低的工况范围为52.13~87.93 kPa。一级混合压差偏高的工况范围为121.74~136.83 kPa,偏低工况范围为95.03~120.67 kPa。
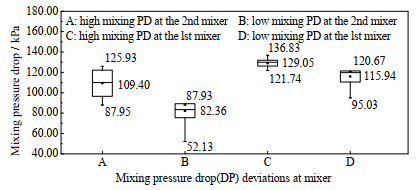
|
图 6 一、二级混合器混合压差偏离情况比较 Fig.6 Comparison of mixing pressure drop (PD) deviations at 1st and 2nd mixers |
操作温度的影响如图 7所示。依据分析结果,建议一级脱盐罐操作温度设为129.64~134.37 ℃,二级脱盐罐操作温度设为127.72~131.59 ℃。而原油温度建议为131.58~136.54 ℃。
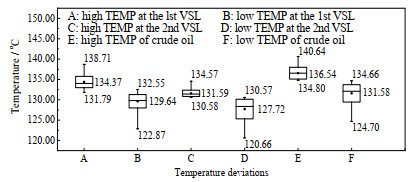
|
图 7 操作温度偏离情况对比 Fig.7 Comparison of operating temperature deviations |
利用本研究提出的电脱盐优化模型,可以依据关键影响因素分析结果提供优化操作方案。依据本研究的优化方案进行优化前后的脱盐后盐的质量浓度对比如图 8所示。按优化操作方案进行调整后,可以使脱盐后盐的质量浓度显著下降。在全部近1 300个工况中,948个工况脱盐后盐的质量浓度超标需要进行优化,其中5个工况无法达到优化目标(盐的质量浓度降至1.3 mg⋅L−1以下),其余均达到优化目标。

|
图 8 优化前后的脱盐效果预测结果比较 Fig.8 Comparison of salt contents before and after optimization |
(1) 提出基于运行参数大数据分析的电脱盐系统智能监测方法,通过建立基于运行参数的脱后盐的质量浓度智能监测模型,有效解决人工采样分析实时性差、对指导优化运行作用不强等问题;
(2) 采用基于贝叶斯的大数据模型结合似然函数分析方法,为开展基于模型的运行参数优化提供依据。提出了基于线性规划的操作参数优化方法,利用该方法对电脱盐的关键因素进行分析与排序,分析了定量的优化操作参数范围;
(3) 与传统的机理分析方法相比,本研究基于装置实际运行数据,考虑全部因素,因而结论的针对性更强,随着运行数据的补充,该方法更具应用前景。但由于模型主要基于运行大数据,当油品或工艺条件发生变化时,原有结论不一定适用于新工况,这是本研究的局限性。
| [1] |
吴应湘, 许晶禹. 油水分离技术[J]. 力学进展, 2015, 45(1): 179-216. WU Y X, XU J Y. Oil and water separation technology[J]. Advances in Mechanics, 2015, 45(1): 179-216. |
| [2] |
涂亚明, 崔明彧. 原油电脱盐效果的影响因素分析[J]. 中国石油和化工标准与质量, 2018, 38(2): 91-93. TU Y M, CUI M Y. Study on the influencing factors of electro-desalting of crude oil[J]. China Petroleum and Chemical Standard and Quality, 2018, 38(2): 91-93. DOI:10.3969/j.issn.1673-4076.2018.02.046 |
| [3] |
陈明燕, 刘政, 聂崇斌, 等. 重质原油电脱盐影响因素分析及操作条件优化研究[J]. 石油与天然气化工, 2011, 40(6): 578-580. CHEN M Y, LIU Z, NIE C B, et al. Analysis of influencing factors and operating optimization for electro-desalting of heavy crude oil[J]. Chemical Engineering of Oil & Gas, 2011, 40(6): 578-580. DOI:10.3969/j.issn.1007-3426.2011.06.009 |
| [4] |
李淑娟. 8Mt/a常减压蒸馏装置腐蚀与防护[J]. 石油化工腐蚀与防护, 2011, 28(5): 27-30. LI S J. Corrosion of a 8.0MM TPY atmospheric - vacuum distillation and protection[J]. Corrosion & Protection in Petrochemical Industry, 2011, 28(5): 27-30. DOI:10.3969/j.issn.1007-015X.2011.05.010 |
| [5] |
朱岳麟, 冯利利, 张艳丽, 等. 原油高频电脱盐机理研究[J]. 石油学报(石油加工), 2006, 22(4): 61-65. ZHU Y L, FENG L L, ZHANG Y L, et al. Study on mechanism of crude oil desalting under high frequency electric field[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2006, 22(4): 61-65. DOI:10.3969/j.issn.1001-8719.2006.04.012 |
| [6] |
徐泽远. 原油电脱盐技术的发展及应用[J]. 石油化工腐蚀与防护, 1996, 13(2): 56-60. XU Z Y. Development & application of electro-desalting technology for crude oil[J]. Corrosion & Protection in Petrochemical Industry, 1996, 13(2): 56-60. |
| [7] |
李天梅, 司小胜, 刘翔, 等. 大数据下数模联动的随机退化设备剩余寿命预测技术[J]. 自动化学报, 2022, 48(9): 2119-2141. LI T M, SI X S, LIU X, et al. Data-model interactive remaining useful life prediction technologies for stochastic degrading devices with big data[J]. Acta Automatica Sinica, 2022, 48(9): 2119-2141. |
| [8] |
刘强, 卓洁, 郎自强, 等. 数据驱动的工业过程运行监控与自优化研究展望[J]. 自动化学报, 2018, 44(11): 1944-1956. LIU Q, ZHUO J, LANG Z Q, et al. Perspectives on data-driven operation monitoring and self-optimization of industrial processes[J]. Acta Automatica Sinica, 2018, 44(11): 1944-1956. |
| [9] |
IZHAR S, FAISAL J, ABDULAZIZ A, et al. Environmental assessment based surface water quality prediction using hyper-parameter optimized machine learning models based on consistent big data[J]. Process Safety and Environmental Protection, 2021, 151: 324-340. DOI:10.1016/j.psep.2021.05.026 |
| [10] |
周海英, 董素荣. 化工过程的故障聚类及诊断空间的分层递阶算法[J]. 测试技术学报, 2008(6): 556-561. ZHOU H Y, DONG S R. Fault cluster of chemical process and hierarchical structure algorithm for diagnosis space[J]. Journal of Test and Measurement Technology, 2008(6): 556-561. |
| [11] |
MOHARM K. State of the art in big data applications in microgrid: A review[J]. Advanced Engineering Informatics, 2019, 42: 100945. |
| [12] |
朱向明, 周凤岐, 武有甫. 基于数据挖掘的防空导弹飞行故障模式决策树[J]. 弹箭与制导学报, 2009, 29(6): 217-220. ZHU X M, ZHOU F Q, WU Y F. Air defense missile flight failure mode decision tree based on data mining model[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(6): 217-220. |
| [13] |
HAN Y M, LIU S, GENG Z Q, et al. Energy analysis and resources optimization of complex chemical processes: Evidence based on novel DEA cross-model[J]. Energy, 2021, 218: 119508. |
| [14] |
ZHANG Y, JI Y H, QIAN H L. Progress in thermodynamic simulation and system optimization of thermochemical conversion process of biomass[J]. Green Chemical Engineering, 2021, 2(3): 266-283. |
| [15] |
赵小强, 周文伟, 惠永永. 基于核熵投影的CPLS间歇过程监测及质量预测[J]. 高校化学工程学报, 2018, 32(5): 1186-1193. ZHAO X Q, ZHOU W W, HUI Y Y. Monitoring and quality prediction of CPLS batch process based on kernel entropy projection[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(5): 1186-1193. |
| [16] |
DANIEL R, EMILY H, BERNARDES G, et al. Adaptive optimization of chemical reactions with minimal experimental information[J]. Cell Reports Physical Science, 2020, 1(11): 1-19. |
| [17] |
NING C, YOU F Q. Optimization under uncertainty in the era of big data and deep learning: When machine learning meets mathematical programming[J]. Computers and Chemical Engineering, 2019, 125(9): 434-448. |
| [18] |
张晓玲, 曹玉苹, 邓晓刚. 基于张量分解的间歇过程故障诊断方法[J]. 高校化学工程学报, 2020, 34(1): 190-199. ZHANG X L, CAO Y P, DENG X G. A fault diagnosis method based on tensor factorization for batch processes[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(1): 190-199. |
| [19] |
CHEN X D, AI Z B, YANG T C, et al. Analysis method of failure likelihood on pressure equipment with combined action of multi-failure mechanism: Proceedings of the ASME 2010 pressure vessels and piping division/K-PVP conference [C]. Bellevue, Washington: ASME 2010 Pressure Vessels and Piping Conference, 2010: 499-504.
|
| [20] |
冀丰偲, 余云松, 张早校. LDA_SVM方法在化工过程故障诊断中的应用[J]. 高校化学工程学报, 2020, 34(2): 487-494. JI F C, YU Y S, ZHANG Z X. Application of LDA and SVM method in fault diagnosis of chemical process[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(2): 487-494. |
| [21] |
中国电子技术标准化研究院, 全国信息技术标准化技术委员会大数据标准工作组. 大数据系列报告之一: 工业大数据白皮书(2019版) [EB/OL]. 2019-04-01 [2021-11-18]. http://www.cesi.cn/images/editor/20190401/20190401145953698.pdf. China Electronics Standardization Institute, The Big Data Standards Working Group of the National Information Technology Standardization Technical Committee. One of the Series Reports on Big Data: Industrial Big Data White Paper (2019 Edition) [EB/OL], 2019-04-01 [2021-11-18]. http://www.cesi.cn/images/editor/20190401/20190401145953698.pdf. |
| [22] |
袁晴棠, 殷瑞钰, 曹湘洪, 等. 面向2035的流程制造业智能化目标、特征和路径战略研究[J]. 中国工程科学, 2020, 22(3): 148-156. YUAN Q T, YIN R Y, CAO X H, et al. Strategic research on the goals, characteristics, and paths of intelligentization of process manufacturing industry for 2035[J]. Strategic Study of Chinese Academy of Engineering, 2020, 22(3): 148-156. |
| [23] |
工业互联网产业联盟. 工业大数据分析指南[EB/OL], [2021-07-24]. http://www.caict.ac.cn/kxyj/qwfb/bps/201902/P020190227355558635820.pdf. Alliance of Industry Internet. Guideline for analysis of industrial big data [EB/OL], (2019) [2021-07-24]. http://www.caict.ac.cn/kxyj/qwfb/bps/201902/P020190227355558635820.pdf. |
| [24] |
中国互联网与工业融合创新联盟, 中国信息通信研究院. "中国制造+互联网"新图景[M]. 北京: 人民邮电出版社, 2016: 36. China Internet and Industry Integration Innovation Alliance, The China Academy of Information and Communications technology. New vision of "made in China + internet"[M]. Beijing: Posts & Telecom Press, 2016: 36. |
| [25] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2017: 147. ZHOU Z H. Machine learning[M]. Beijing: Tsinghua University Press, 2017: 147. |
| [26] |
BISHOP C. Pattern recognition and machine learning[M]. Singapore: Springer, 2006.
|
| [27] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 37. LI H. Statistical learning method[M]. Beijing: Tsinghua University Press, 2012: 37. |
| [28] |
朱建新, 陈学东, 吕宝林, 等. 基于多维高斯贝叶斯的机械设备失效/故障智能诊断及参数影响分析[J]. 机械工程学报, 2020, 56(4): 35-41. ZHU J X, CHEN X D, LYU B L, et al. Smart failure/fault diagnosis and influence analysis for mechanical equipment with multivariate Gaussian Bayesian method[J]. Journal of Mechanical Engineering, 2020, 56(4): 35-41. |




