近年来,纳米技术的进步促进了针对不同疾病的新型纳米药物和诊疗方法的迅猛发展,极大地增强了药物的靶向性和有效性[1-3]。然而,人体内的内皮网状系统(reticuloendothelial system,RES)对外源纳米颗粒(nanoparticles,NPs)的非特异性摄取却阻碍了纳米医学的临床转化进程[4]。肝脏是人体最重要的代谢器官,位于肝窦(liver sinusoid)内壁上的肝脏驻留巨噬细胞-库普弗细胞(Kupffer cells)[5-6]和肝窦内皮细胞(liver sinusoidal endothelial cells,LSECs)[7]是肝内RES系统的重要组成。对抗肿瘤新型纳米药物的研究发现,进入血液中的30%~99% 的纳米粒子会被肝脏摄取并快速清除,平均只有不到1% 能够到达实体肿瘤病灶部位[8]。这不仅严重降低了纳米药物的生物利用度,还可能引发肝毒性进而造成肝损伤[9]。为了减少肝脏对纳米药物的非特异性清除,延长其在血液循环中的半衰期,目前常用的策略之一是对纳米粒子进行改性,通过改变纳米粒子的尺寸[10-11]、形状[12-15]、弹性[16]、表面电荷[17]及进行表面化学修饰等[18-21]来减少细胞对纳米粒子的摄取。另一个策略是调控肝窦内血流速度[22]或RES细胞的状态[5, 23],进而降低RES系统对纳米粒子的“捕获”。但是在评价这2种策略对纳米粒子肝脏清除的影响时,往往忽视其在窦内血液中的运动特性产生的影响,因而研究纳米粒子在肝窦内的运动规律也是调控纳米药物肝脏清除率的重要途径和手段。
肝窦是肝脏内部相邻肝板之间的特殊毛细血管,其结构细微且复杂[24],因此很难以常规的实验手段观察纳米粒子在肝窦内的运动状况。近年来,采用数学建模方法模拟预测纳米粒子在动物及人血管内运动及代谢规律的相关研究取得了重大进展[25-26]。Lunnoo等[27]构建了一个二维动脉血管模型,利用欧拉-拉格朗日法模拟了10 nm~4 μm的磁性纳微米粒子在其中随血液的流动,考察了粒子尺寸、壳层种类对其靶向性的影响。Fullstone等[28]利用将基于主体模型(agent-based model,ABM)和计算流体力学(computational fluid dynamics,CFD)相结合的方法,建立三维直形毛细血管模型并模拟了红细胞和纳米粒子在管内运动轨迹,考察了红细胞比容对纳米粒子运动和分散规律的影响。Tsoi等[29]利用简单直管型肝窦模型,研究了血流速度、颗粒尺寸对硬质纳米粒子在肝脏中清除率的影响。然而,现有模型都未能体现肝窦的弯曲结构及宽窄不均生理特征,因此本研究首次提出并建立不规则的小鼠肝窦模型,采用欧拉-拉格朗日分散型两相流方法模拟具有不同物化特性的纳米粒子在肝窦内的运动特性及其与肝窦内壁的碰撞规律,结合纳米粒子与窦壁上细胞的相互作用,考察不同粒子的运动对肝脏清除率的影响。研究结果将有助于深入理解纳米粒子肝脏清除机制,设计并开发出具有高生物利用度、肝外靶向性以及更低肝毒性的新型纳米药物。
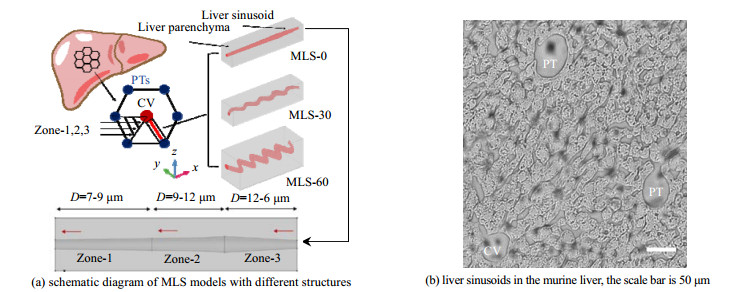
2 模型构建 2.1 构建小鼠肝窦几何模型如图 1(a)所示,肝脏的内部由众多肝小叶单元组成,可简化为典型的六边形(多角棱柱状)结构[30]。血液从门脉三联管(portal vein triads,PTs)中的门静脉和肝动脉流入,流经肝窦后从中央静脉(central vein,CV)流出。因此作为相邻肝细胞板之间的微血管网,肝窦是纳米粒子与肝脏内细胞作用的主要场所。本研究参考小鼠的肝窦生理特征[31],利用AutoCAD构建了3种代表不规则结构的小鼠肝窦模型(murine liver sinusoid model,MLS)。一是直形的MLS-0模型,如图 1(a)所示,该模型的肝窦直径为6~12 μm,模拟了在肝小叶3个区域内肝窦直径的生理变化,在入口和出口附近较为狭窄,而在中间区域较宽[24],肝窦的长度设定为200 μm[24]。为了模拟肝脏中部分肝窦存在的不规则弯曲结构(图 1(b)),又在MLS-0模型的基础上设计了30°和60°弯曲角度,即MLS-30和MLS-60弯管模型(图 1(a))。3种肝窦模型的直径变化相同,路径长度保持一致。肝窦外侧为包裹单排列的大小20 μm的肝实质细胞[31],因此,3种模型的边界设为宽和高都为40 μm的长方体单元。
|
图 1 小鼠肝窦(MLS)模型几何结构示意图 Fig.1 Schematic diagram of murine liver sinusoid models |
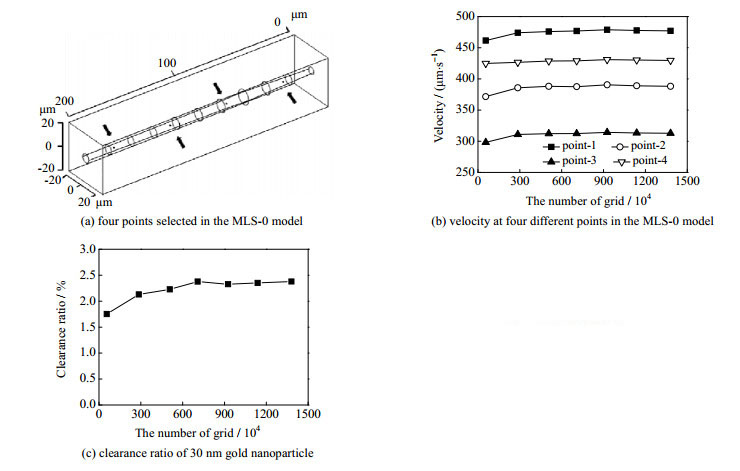
将在AutoCAD中构建好的MLS模型导入COMSOL Multiphysics 5.5软件。采用非结构化网格对其进行网格划分,为了提高计算精确度,进行了网格无关性检验。根据小鼠的生理窦内压差(约80 Pa)[32],设定入口压力为93.3 Pa,出口压力为13.3 Pa,流体的离散格式为P1+P1,并在50万~1 500万的网格数之间进行了模拟计算。选择MLS-0模型肝窦区域内,y轴坐标和z轴坐标都为0 μm,x轴坐标依次为25、75、125、175 μm的4个不同位置(图 2(a))处的血液流速和30 nm金纳米粒子在模型中的清除率作为衡量的参数。随着网格数目的不断增加,各点处的流速(图 2(b))和30 nm金纳米粒子的清除率(图 2(c))的计算结果逐渐趋于稳定。当网格数目为900万左右时,流速和清除率的相对误差都小于1%。此时可以认为网格对模拟结果的影响非常小,因此采用900万网格数目作为后续模拟的网格划分方案。MLS-30,MLS-60模型的网格设置同MLS-0模型一致。
|
图 2 网格无关性检验 Fig.2 Grid independence verification |
考虑到纳米粒子极小的尺寸以及肝窦内较低的血液流动环境,尽可能排除影响较小的因素以降低计算的复杂性,因此在模拟中做出如下假设:
(1) 由于纳米粒子的尺寸较小,其在肝窦内的体积分数一般小于0.1%,因此纳米粒子之间的微观作用力(如范德华力,静电作用力)以及纳米粒子之间的相互碰撞被忽略。纳米粒子的颗粒雷诺数较小(Rep < 1)[33],因此主要考虑流体对粒子的作用力,而粒子对流体的反作用力不被考虑,此时纳米粒子运动和血液流动之间的耦合为弱耦合。
| $ R{e_{\rm{p}}} = \frac{{{d_{\rm{p}}}{u_{\rm{p}}}{\rho _{\rm{b}}}}}{{{\mu _{\rm{b}}}}} $ | (1) |
(2) 肝窦内的红细胞压积数仅为10% 左右[25],且红细胞具有与肝窦直径相似的大小,因此不考虑红细胞对纳米粒子的边缘化作用[26]。
(3) 模拟的过程被认为是在正常生理情况下发生,因此体系的热力学温度T被设定为310.15 K(37 ℃)。
3.2 血液的控制方程血液作为纳米粒子流动的载体是典型的非牛顿流体,具有剪切稀化的性质,利用卡罗(Carreau)模型[34]对其进行描述:
| $ \mu = {\mu _{\inf }} + ({\mu _0} - {\mu _{\inf }}){\left[ {1 + {{(\lambda \gamma )}^2}} \right]^{\frac{{n - 1}}{2}}} $ | (2) |
由于肝窦的尺寸较小,且其中的血液流速较低,其雷诺数Re远小于1,血液的流动形式是斯托克斯流动,即蠕动流,由忽略惯性项的不可压缩的纳维-斯托克斯(Navier-Stokes)方程以及连续性方程描述:
| $ \nabla \cdot \left[ { - \nabla p + \mu \left( {\nabla \mathit{\boldsymbol{u}} + {{(\nabla \mathit{\boldsymbol{u}})}^{\rm{T}}}} \right)} \right] = 0$ | (3) |
| $ \nabla \cdot {\rho _{\rm{b}}} \cdot (u) = 0 $ | (4) |
由于肝窦的血液可以通过肝窦内皮细胞以及Disse空间向肝实质内发生渗透,使血液的流速变慢,因而在模型中考虑肝实质区域的流动,将更贴近于肝脏内部的真实生理环境。本研究将肝实质区域设置为由布林克曼(Brinkman)方程控制的多孔介质流动区域[35]。与传统的达西(Darcy)方程相比,它能够体现出流体从肝窦到肝实质的速度变化。
| $ 0 = \nabla \cdot \left[ { - \nabla p + K} \right] - ({\mu _{\rm{L}}}{\kappa ^{ - 1}} + {\beta _{\rm{F}}}\left| u \right| + \frac{{{q_m}}}{{\varepsilon _{\rm{p}}^2}})u $ | (5) |
| $ {\rho _{\rm{b}}}\nabla \cdot u = {q_m} $ | (6) |
| $ K = \mu \frac{1}{{{\varepsilon _{\rm{p}}}}}(\nabla \mathit{\boldsymbol{u}} + {(\nabla \mathit{\boldsymbol{u}})^{\rm{T}}}) - \frac{2}{3}\mu \frac{1}{{{\varepsilon _{\rm{p}}}}}\nabla (\nabla \cdot \mathit{\boldsymbol{u}}) $ | (7) |
利用拉格朗日方法对纳米粒子的运动进行了模拟,每个纳米粒子被视为一个质点,并进行单独跟踪。所有的粒子都被认为是球形粒子,它们的运动主要受布朗运动力、曳力和重力控制[36-38]。布朗运动力由高斯白噪声公式描述,曳力由斯托克斯(Stokes)曳力公式描述。根据牛顿第二定律,通过对时间积分得到模型中纳米粒子的运动轨迹和速度
| $ {F_{\rm{B}}} = \xi \sqrt {\frac{{12\pi k\mu T{r_{\rm{p}}}}}{{\Delta T}}} $ | (8) |
| $ {F_{\rm{D}}} = \frac{{18\mu }}{{{\rho _{\rm{p}}}d_{\rm{p}}^2}}{m_{\rm{p}}}(u - {u_{\rm{p}}}) $ | (9) |
| $ {F_{\rm{B}}} = {m_{\rm{p}}}g $ | (10) |
| $ \frac{{{\rm{d}}({m_{\rm{p}}}{u_{\rm{p}}})}}{{{\rm{d}}t}} = {F_{\rm{B}}} + {F_{\rm{D}}} + {F_{\rm{g}}} $ | (11) |
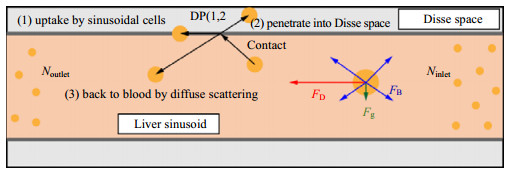
3种模型都分别选用物化特性相同的4 000个纳米粒子,追踪模拟其1 s内持续从肝窦模型入口处随机释放过程。该过程可根据研究的需求进行设定,如同时释放不同粒径或数量的真实纳米粒子悬浮液。如图 3所示,模拟过程中纳米粒子随血流运动并与壁面发生碰撞,可看作是纳米粒子与肝窦内壁细胞发生了接触。接触后的纳米粒子如果被肝窦内壁细胞摄取,或者穿过LSECs上的微小窗孔以及LSECs之间的间隙进入窦周间隙(Disse空间),可认为该纳米粒子从血液中消失,即被肝脏清除。将发生这2种情况的概率称为消失概率(disappearing probability,DP)。而那些与细胞接触但没有被清除的纳米粒子则被认为撞击到壁面后通过漫反射回到血流之中,这种情况发生的概率为1−DP。消失概率DP主要取决于纳米粒子的物化特性以及与肝窦内壁细胞接触后两者相互作用方式和能力。模拟中将同次释放纳米粒子的DP设置为相同数值。
|
图 3 纳米粒子在肝窦内的受力分析以及其与肝窦壁上细胞的相互作用设定 Fig.3 Stress analysis of nanoparticles in liver sinusoid and interaction settings with liver sinusoidal cells |
通过对各个模型到达出口纳米粒子数量进行统计,可计算出纳米粒子每次流经3种MLS模型后被肝脏清除的比率,即清除率(clearance ratio,CR)。当设定不同物化特性的纳米粒子DP值相同时,模型中的CR值将只与纳米粒子在肝窦中运动特性有关,进而可通过CR的数值大小来评价不同纳米粒子的运动特性对其肝脏清除的影响。
| ${\rm{CR}} = 1 - \frac{{{N_{{\rm{outlet}}}}}}{{{N_{{\rm{inlet}}}}}} \times 100\% $ | (12) |
如表 1所示,模拟中所有参数都按照小鼠的生理参数设定。
|
|
表 1 MLS模型中的模拟参数 Table 1 Simulation parameters used in MLS models |
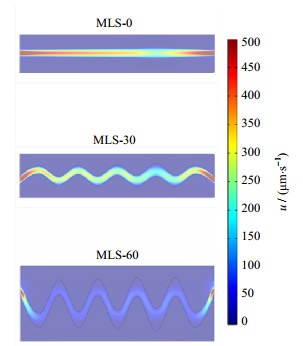
图 4为3种不同MLS模型中肝窦内血液流动的模拟结果,结果显示MLS-0,MLS-30,MLS-60中窦内血液的平均流速分别为215、160和80 μm⋅s−1,符合小鼠肝窦血液流速的生理范围(< 500 μm⋅s−1)[29]。其中MLS-0模拟生理解剖结构为进、出口窄,中间宽的直形肝窦,直径的变化可引起窦内血液流速的变化,较窄的入口和出口处血液流速高于直径较大的中间区域,可更好地仿真此类肝窦内的血流。而在直径变化的基础上,MLS-30和MLS-60模拟生理解剖结构弯的肝窦。模拟结果显示,MLS-30和MLS-60中的血液流速低于MLS-0模型,并且在弯曲处出现了流速极低的“死区”,其范围随着肝窦的弯曲角度增大而扩大。因此,与现有的内径保持一致的直管肝窦几何模型相比,本研究建立的3种仿真MLS模型更加真实地代表了动物体内肝窦结构及内部血液流动的多样性和复杂性。
|
图 4 流场计算结果 Fig.4 Calculation results of the flow fields |
选用直径在5~250 nm的金纳米粒子作为模型材料,该尺寸范围内的纳米粒子最适于作为体内纳米药物递送的载体,小于5 nm的纳米粒子会通过肾脏快速排泄,而大于250 nm的纳米粒子将会更容易激活体内补体系统而优先被RES识别并消除[41]。根据文献[42]及静态细胞摄取实验的模拟结果(前期工作)确定DP值小于10%,在模拟中首先设定为0.3%。
在3种MLS模型中,不同尺寸的金纳米粒子与肝窦壁面碰撞后消失的纳米粒子的碰撞位点分布如图 5(a)所示。其中5 nm的金纳米粒子碰撞位点分布最为广泛,其次是30和250 nm。究其原因,纳米粒子的尺寸越小,扩散系数越大,因而更容易在布朗运动力的作用下与壁面发生碰撞。由图 5(b)可见,当不同尺寸纳米粒子经过MLS-0同一横截面时,尺寸越小运动范围越大。Sykes等[43]对金纳米粒子在肿瘤基质内部的传递过程的研究中获得相同发现,即颗粒尺寸能够有效调节纳米粒子在流体中的扩散能力,越小的纳米粒子其扩散能力越强。而随着粒径的增加,金纳米粒子碰撞位点分布在直形的MLS-0模型和弯形的MLS-30和MLS-60模型上出现了差异。体现在纳米粒子会逐渐聚集在具有弯曲结构的肝窦处,并随着弯度增加而变得明显(图 5(a))。在小鼠活体成像实验中发现,纳米粒子通过静脉注射进入肝脏后,会逐渐聚集在具有弯曲结构的肝窦处,证实了这种集中分布模式的存在[44]。这是由于肝窦内粒子所受曳力的方向始终与流体流动的方向一致,导致纳米粒子不可避免地碰撞(惯性碰撞)到肝窦的弯曲部位。如图 5(b)所见,当纳米粒子经过MLS-60的弯曲部位时,纳米粒子会在曳力惯性的作用下向着弯曲一侧偏移。并且考虑到大尺寸纳米粒子质量越大,所受惯性也就越大,因此向弯曲处偏移的程度也就越大。

|
图 5 不同尺寸的金纳米粒子在MLS模型中与肝窦壁面的碰撞模式 Fig.5 Collision models of different size gold nanoparticles with liver |
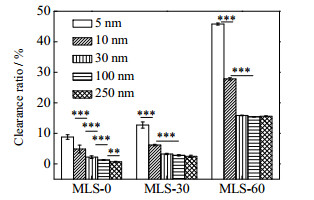
如图 6所示,在MLS-0模型中,金纳米粒子的清除率随着粒径减小而增加,这正是由于小尺寸纳米粒子的扩散能力强所致。随着肝窦弯度的增加,纳米粒子在MLS-30和MLS-60中的清除率都出现了显著增加,这与前文中阐述的纳米粒子在弯曲结构中运动产生的由曳力惯性引发的碰撞接触增多相关联。尽管在这2个模型中,5和10 nm的金纳米粒子的清除率明显高于其他3种大尺寸的纳米粒子,但在MLS-30模型中,30到250 nm的金纳米粒子的清除率差异缩小了,而在MLS-60中已经无显著性差异。这是因为尺寸大的纳米粒子会产生更强的惯性碰撞,从而增加它们与壁面的接触频率,提高其肝脏清除率。肝窦弯度的增加将会使这个现象变得更为明显。从模拟结果看,传统的简单直管肝窦模型或者直径有变化MLS-0模型都显示了纳米粒子的扩散能力对其清除率的决定性作用,即肝脏更容易清除扩散能力强的小尺寸纳米粒子。但真实肝窦结构复杂且存在不同程度的弯曲,反而对扩散能力弱、惯性强的大尺寸纳米粒子的清除率增加了。因此,从纳米粒子运动特性角度考虑,在更为复杂真实的肝窦中,扩散能力和惯性都较弱的中等尺寸纳米粒子与肝窦壁面上细胞的接触频率会更低一些,这将有利于延长其在血液中循环的时间。一些体外研究证明,50 nm是细胞对纳米粒子摄取的最佳尺寸,较小颗粒(15~30 nm)和较大颗粒(70~240 nm)的纳米粒子的细胞摄取水平相对较低[45]。然而De Jong等[10]、Ouyang等[46]和Poon等[47]的实验研究表明,小鼠肝脏对50 nm的金纳米粒子清除率要显著低于15、100和250 nm的金纳米粒子。这可能是因为50 nm的纳米粒子在肝窦内的运动有效地降低了其与Kupffer细胞以及LSECs的接触频率。
|
图 6 不同尺寸的金纳米粒子在MLS模型中的清除率。数据点和误差条表示为平均值±标准偏差。双尾学生t检验用于计算p值,***p < 0.001,** p < 0.01,*p < 0.05,NS表示差异无统计学意义,每种模拟重复3次(n=3) Fig.6 Clearance ratios of different size gold nanoparticles in the MLS models (Data points and error bars are presented as mean ± standard deviation Two-tailed Student's t-test was used to calculate the p value, ***p < 0.001, ** p < 0.01, *p < 0.05, and NS stands for statistically insignificant difference, each simulation was repeated three times(n=3)). |
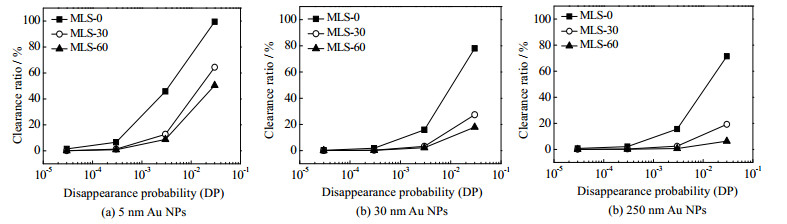
在上述研究中,设定不同尺寸纳米粒子的DP值为0.3%,探究了颗粒尺寸在纳米粒子运动中对其肝脏清除效率的影响。设计纳米药物时,通过对相同尺寸纳米粒子的表面修饰可改变其与肝窦内壁细胞相互作用能力,进而改变肝脏对其清除率[48]。在MLS模型中,作者通过调整DP值(0.003%~3%)考察了纳米粒子与肝窦内壁细胞相互作用能力变化对5、30和250 nm粒子肝脏清除率的影响。如图 7所示,随着消失概率DP的提高,MLS模型中纳米粒子的清除率都出现了明显的增加。DP值变化相同时,MLS-60中纳米粒子的清除率增加最多,其次是MLS-30,而在MLS-0模型中清除率的增量最少。这意味着肝窦的弯曲结构会显著放大DP值对纳米粒子肝脏清除率的影响。此外,作者发现无论在哪种MLS模型,随着DP的增加,5 nm的金纳米粒子的清除率都显著增加,其次是30和250 nm。说明DP对不同尺寸纳米粒子肝脏清除效率的影响并不是等效的,小尺寸纳米粒子的清除率受DP影响更大。究其原因,倾向于扩散碰撞的小尺寸纳米粒子与窦壁上细胞接触的粒子数目更多,且范围更广,但是从单个纳米粒子的角度来看,其与细胞发生碰撞的次数却少于发生惯性碰撞的大尺寸纳米粒子。当消失概率DP逐渐增大时,扩散碰撞所具有的数目优势能够较快地增加纳米粒子的清除率。反之,则降低。
|
图 7 消失概率DP对不同尺寸的金纳米粒子清除率的影响 Fig.7 Effects of disappearance probability (DP) on clearance ratios of gold nanoparticles with different sizes |
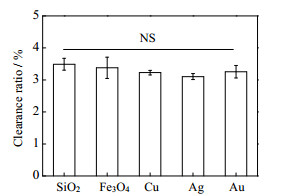
由于纳米粒子的种类不同,其自身密度也各不相同。本研究所选用的金纳米粒子是一种密度较大的无机纳米粒子(19 320 kg⋅m−3)。为了比较纳米粒子密度对其窦内运动的影响,本研究还模拟了几种密度较小且常用于体内药物输送的无机纳米粒子,即SiO2纳米粒子(2 200 kg⋅m−3),超顺磁Fe3O4纳米粒子(5 180 kg⋅m−3),铜纳米粒子(8 900 kg⋅m−3),以及银纳米粒子(10 530 kg⋅m−3) 在MLS-30模型中的运动。图 8表示当消失概率为0.3%,粒径为30 nm时,纳米粒子的清除率不随着密度的逐渐增大而改变。这意味着密度并不会通过改变纳米粒子的运动状态而影响其肝脏清除率。究其原因,使纳米粒子与壁面接触的布朗运动力和曳力的惯性并不受粒子密度的影响。
|
图 8 不同密度的30 nm纳米粒子的流经MLS-30模型后的清除率。数据点和误差条表示为平均值±标准偏差。双尾学生 t检验用于计算p值。***p < 0.001,** p < 0.01,*p < 0.05,NS表示差异无统计学意义,每种模拟重复3次(n=3)。 Fig.8 Clearance ratios of 30 nm nanoparticles with different densities after passing through the MLS-30 model (Data points and error bars are presented as mean ± standard deviation. Two-tailed Student's t-test was used to calculate the p value, ***p < 0.001, ** p < 0.01, *p < 0.05, and NS stands for statistically insignificant difference, each simulation was repeated three times(n=3)). |
(1) 纳米粒子与直形的肝窦模型(MLS-0)内壁的碰撞主要由粒子布朗运动力(扩散)主导,因此碰撞位点会随着纳米颗粒尺寸的增加而减少;在弯形的MLS-30和MLS-60模型中,纳米粒子与窦壁的碰撞除由扩散引发外,还会产生因曳力惯性导致的碰撞。惯性碰撞位点不仅会随着颗粒尺寸的增大而增多,还会向弯曲的肝窦结构处聚集,且弯度越大聚集现象越显著。随着肝窦弯曲程度的增加,那些扩散能力弱,但惯性强的大尺寸纳米粒子的清除率的增量更多。
(2) 在3种模型中粒径较小的纳米粒子的清除率对DP值变化的响应最大。同时在弯形的MLS-30和MLS-60模型中,弯曲程度越大,纳米粒子的清除率对DP值的变化的响应也越大。
(3) 在50到250 nm颗粒尺寸范围内,颗粒密度对纳米粒子在肝窦内运动的影响十分有限,因此对纳米粒子的肝脏清除率几乎不会产生影响。
符号说明:
dp
⎯ 纳米粒子的直径,nm
∆T
⎯ 纳米粒子运动的时间步长
drr, dzz, dθθ
⎯ 渗透参数,m2
u
⎯ 血液的流速,μm⋅s−1
FB, FD, Fg
⎯ 分别为纳米粒子所受到的布朗运动力,曳力和重力,N
up
⎯ 纳米粒子相对于流体的速度,μm⋅s−1
g
⎯ 重力加速度,m⋅s−2
βF
⎯ 等温压缩率
mp
⎯ 纳米粒子的质量,μg
γ
⎯ 剪切速率,dyn⋅cm−2
n
⎯ 幂率指数
εp
⎯ 肝实质区域的孔隙度
Ninlet
⎯ 模型入口释放的纳米粒子数目
κ
⎯ 肝实质区域的渗透率,md
Noutlet
⎯ 到达模型出口的纳米粒子数目
λ
⎯ 时间常数
K
⎯ 黏性应力,N
μ
⎯ 血液的动力黏度,Pa⋅s
k
⎯ 波尔兹曼常数,J⋅K−1度,Pa⋅s
μ0, μinf
⎯ 分别为当剪切速率趋于无穷大和零时的动力黏
p
⎯ 血液的压力,Pa
μb
⎯ 血液的动态黏度,Pa⋅s
pinlet, poutlet
⎯ 分别为肝窦入口处、出口处压力,Pa
μL
⎯ 肝实质内组织液的动态黏度,Pa⋅s
qm
⎯ 流体的质量流量,kg⋅m−3
ξ
⎯ 服从标准正态分布的高斯随机数
Re
⎯ 雷诺数
ρb
⎯ 血液密度,kg⋅m−3
Rep
⎯ 颗粒雷诺数
ρL
⎯ 肝实质密度,kg⋅m−3
rp
⎯ 纳米粒子的半径,nm
ρp
⎯ 纳米粒子的密度,kg⋅m−3
| [1] |
康垚, 王素真, 樊江莉, 等. 无机纳米药物载体在肿瘤诊疗中的研究进展[J]. 化工学报, 2018, 69(1): 128-140. KANG Y, WANG S Z, FAN J L, et al. Progress in inorganic nanomedicine carriers for tumor diagnosis and treatments[J]. CIESC Journal, 2018, 69(1): 128-140. |
| [2] |
覃志忠, 宋秀娟, 张凤宝, 等. 5-氟脲嘧啶载O-羧甲基壳聚糖自组pH敏感纳米粒的体外释放[J]. 高校化学工程学报, 2010, 3(24): 488-491. QIN Z Z, SONG X J, ZHANG F B, et al. Self-assembled nanoparticles based on 5β-cholanic acid/O-carbohydrate chitosan/sulfonamide as a novel carrier for 5-fluorouracil[J]. Journal of Chemical Engineering of Chinese Universities, 2010, 3(24): 488-491. |
| [3] |
赵海田, 李旭东, 曹凤芹, 等. 基于壳聚糖纳米粒子载药体系的制备与应用研究进展[J]. 化工进展, 2019, 38(11): 5057-5065. ZHAO H T, LI X D, CAO F Q, et al. Advances on preparation and application of chitosan-based nanoparticles for drug delivery system[J]. Chemical Industry and Engineering Progress, 2019, 38(11): 5057-5065. DOI:10.16085/j.issn.1000-6613.2019-0334 |
| [4] |
BLANCO E, SHEN H, FERRARI M. Principles of nanoparticle design for overcoming biological barriers to drug delivery[J]. Nature Biotechnology, 2015, 33(9): 941-951. DOI:10.1038/nbt.3330 |
| [5] |
TAVARES A J, POON W, ZHANG Y N, et al. Effect of removing Kupffer cells on nanoparticle tumor delivery[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(51): 71-80. |
| [6] |
MIRSHAFIEE V, SUN B B, CHANG C H, et al. Toxicological profiling of metal oxide nanoparticles in liver context reveals pyroptosis in kupffer cells and macrophages versus apoptosis in hepatocytes[J]. ACS Nano, 2018, 12: 3836-3852. DOI:10.1021/acsnano.8b01086 |
| [7] |
HUNT N J, LOCKWOOD G P, LE COUTEUR F H, et al. Rapid intestinal uptake and targeted delivery to the liver endothelium using orally administered silver sulfide quantum dots[J]. ACS Nano, 2020, 14(2): 1492-1507. DOI:10.1021/acsnano.9b06071 |
| [8] |
ZHANG Y N, POON W, TAVARES A J, et al. Nanoparticle–liver interactions: Cellular uptake and hepatobiliary elimination[J]. Journal of Controlled Release, 2016, 240: 332-348. DOI:10.1016/j.jconrel.2016.01.020 |
| [9] |
LI X M, HU Z P, MA J L, et al. The systematic evaluation of size-dependent toxicity and multi-time biodistribution of gold nanoparticles[J]. Colloids and Surface B: Biointerfaces, 2018, 167: 260-266. DOI:10.1016/j.colsurfb.2018.04.005 |
| [10] |
DE JONG W H, HAGENS W I, KRYSTEK P, et al. Particle size-dependent organ distribution of gold nanoparticles after intravenous administration[J]. Biomaterials, 2008, 29(12): 1912-1919. DOI:10.1016/j.biomaterials.2007.12.037 |
| [11] |
ABDELHALIM M A K, JARRAR B M. Histological alterations in the liver of rats induced by different gold nanoparticle sizes, doses and exposure duration[J]. Journal of Nanobiotechnology, 2012, 10(5): 1-9. |
| [12] |
YU T, HUBBARD D, RAY A, et al. In vivo biodistribution and pharmacokinetics of silica nanoparticles as a function of geometry, porosity and surface characteristics[J]. Journal of Controlled Release, 2012, 163(1): 46-54. DOI:10.1016/j.jconrel.2012.05.046 |
| [13] |
HUANG X, LI L, LIU T, et al. The shape effect of mesoporous silica nanoparticles on biodistribution, clearance, and biocompatibility in vivo[J]. ACS Nano, 2011, 5(7): 5390-5399. DOI:10.1021/nn200365a |
| [14] |
TALAMINI L, VIOLATTO M B, CAI Q, et al. Influence of size and shape on the anatomical distribution of endotoxin-free gold nanoparticles[J]. ACS Nano, 2017, 11(6): 5519-5529. DOI:10.1021/acsnano.7b00497 |
| [15] |
LIU Y, LIU Y, WANG Z, et al. Suppressing nanoparticle-mononuclear phagocyte system interactions of two-dimensional gold nanorings for improved tumor accumulation and photothermal ablation of tumors[J]. ACS Nano, 2017, 11(10): 10536-10548. |
| [16] |
ANSELMO A C, ZHANG M, KUMAR S, et al. Elasticity of nanoparticles influences their blood circulation, phagocytosis, endocytosis, and targeting[J]. ACS Nano, 2015, 9(3): 3169-3177. DOI:10.1021/acsnano.5b00147 |
| [17] |
ELCI S G, JIANG Y, YAN B, et al. Surface charge controls the suborgan biodistributions of gold nanoparticles[J]. ACS Nano, 2016, 10(5): 5536-5542. DOI:10.1021/acsnano.6b02086 |
| [18] |
LI X, WANG B, ZHOU S, et al. Surface chemistry governs the sub-organ transfer, clearance and toxicity of functional gold nanoparticles in the liver and kidney[J]. Journal of Nanobiotechnology, 2020, 18(1): 1-16. DOI:10.1186/s12951-019-0560-5 |
| [19] |
ZHOU H, FAN Z, LI P Y, et al. Dense and dynamic polyethylene glycol shells cloak nanoparticles from uptake by liver endothelial cells for long blood circulation[J]. ACS Nano, 2018, 12(10): 10130-10141. DOI:10.1021/acsnano.8b04947 |
| [20] |
VAN HAUTE D, LIU A T, BERLIN J M. Coating metal nanoparticle surfaces with small organic molecules can reduce nonspecific cell uptake[J]. ACS Nano, 2018, 12(1): 117-127. DOI:10.1021/acsnano.7b03025 |
| [21] |
ZHANG Y, LIU A T, CORNEJO Y R, et al. A systematic comparison of in vitro cell uptake and in vivo biodistribution for three classes of gold nanoparticles with saturated PEG coatings[J]. PLOS ONE, 2020, 15(7): 1-16. |
| [22] |
LI Y, WAN J, WANG F, et al. Effect of increasing liver blood flow on nanodrug clearance by the liver for enhanced antitumor therapy[J]. Biomaterials Science, 2019, 7(4): 1507-1515. DOI:10.1039/C8BM01371C |
| [23] |
NIKITIN M P, ZELEPUKIN I V, SHIPUNOVA V O, et al. Enhancement of the blood-circulation time and performance of nanomedicines via the forced clearance of erythrocytes[J]. Nature Biomedical Engineering, 2020, 4(7): 717-731. DOI:10.1038/s41551-020-0581-2 |
| [24] |
MCCUSKEY R S. Morphological mechanisms for regulating blood flow through hepatic sinusoids[J]. Liver, 2000, 20(1): 3-7. DOI:10.1034/j.1600-0676.2000.020001003.x |
| [25] |
LIU Z, ZHU Y, RAO R R, et al. Nanoparticle transport in cellular blood flow[J]. Computers and Fluids, 2018, 172: 609-620. DOI:10.1016/j.compfluid.2018.03.022 |
| [26] |
LIU Z, CLAUSEN J R, REKHA R R, et al. A unified analysis of nano-to-microscale particle dispersion in tubular blood flow[J]. Physics of Fluids, 2019, 31(8): 1-11. |
| [27] |
LUNNOO T, PUANGMALI T. Capture efficiency of biocompatible magnetic nanoparticles in arterial flow: A computer simulation for magnetic drug targeting[J]. Nanoscale Research Letters, 2015, 10(1): 1-11. DOI:10.1186/1556-276X-10-1 |
| [28] |
FULLSTONE G, WOOD J, HOLCOMBE M, et al. Modelling the transport of nanoparticles under blood flow using an agent-based approach[J]. Scientific Reports, 2015, 5: 1-13. DOI:10.9734/JSRR/2015/14076 |
| [29] |
TSOI K M, MACPARLAND S A, MA X Z, et al. Mechanism of hard-nanomaterial clearance by the liver[J]. Nature Materials, 2016, 15(11): 1212-1221. DOI:10.1038/nmat4718 |
| [30] |
WAKE K, SATO T. "The Sinusoid" in the Liver: Lessons learned from the original definition by charles sedgwick minot (1900)[J]. Anatomical Record, 2015, 298(12): 2071-2080. DOI:10.1002/ar.23263 |
| [31] |
FU X, SLUKA J P, CLENDENON S G, et al. Modeling of xenobiotic transport and metabolism in virtual hepatic lobule models[J]. PLOS ONE, 2018, 13(9). |
| [32] |
XIE C, WEI W, ZHANG T, et al. Monitoring of systemic and hepatic hemodynamic parameters in mice[J]. Journal of Visualized Experiments, 2014(92): 7-13. |
| [33] |
ZHANG J, YAN S, YUAN D, et al. Fundamentals and applications of inertial microfluidics: A review[J]. Lab on a Chip, 2016, 16(1): 10-34. DOI:10.1039/C5LC01159K |
| [34] |
PIERGIOVANNI M, BIANCHI E, CAPITANI G, et al. Microcirculation in the murine liver: a computational fluid dynamic model based on 3D reconstruction from in vivo microscopy[J]. Journal of Biomechanics, 2017, 63: 125-134. DOI:10.1016/j.jbiomech.2017.08.011 |
| [35] |
MOSHARAF-DEHKORDI M. A fully coupled porous media and channels flow approach for simulation of blood and bile flow through the liver lobules[J]. Computer Methods in Biomechanics and Biomedical Engineering, 2019, 22(9): 901-915. DOI:10.1080/10255842.2019.1601180 |
| [36] |
KIM M M, ZYDNEY A L. Effect of electrostatic, hydrodynamic, and Brownian forces on particle trajectories and sieving in normal flow filtration[J]. Journal of Colloid and Interface Science, 2004, 269(2): 425-431. DOI:10.1016/j.jcis.2003.08.004 |
| [37] |
戴忠平. 纳米流体在管道内的流动特性研究[D]. 杭州: 中国计量大学, 2016. DAI Z P. Investigation of flow characteristics of nanofluids in the tube [D]. Hangzhou: China Jiliang University, 2016. |
| [38] |
BUONGIORNO J. Convective transport in nanofluids[J]. Journal of Heat Transfer, 2006, 128(3): 240-250. DOI:10.1115/1.2150834 |
| [39] |
HU J, LÜ S, FENG S, et al. Flow dynamics analyses of pathophysiological liver lobules using porous media theory[J]. Acta Mechanica Sinica, 2017, 33(4): 823-832. DOI:10.1007/s10409-017-0674-7 |
| [40] |
DING W, LIU S, LI S, et al. Simulation of blood and oxygen distributions in a hepatic lobule with sinusoids obstructed by cancer cells[J]. Journal of Theoretical Biology, 2018, 446: 229-237. DOI:10.1016/j.jtbi.2018.03.016 |
| [41] |
NAZANIN H, SAMANTHA G, HONGBIN H, et al. The effect of nanoparticle size on in vivo pharmacokinetics and cellular interaction[J]. Nanomedicine, 2016, 11(6): 673-692. DOI:10.2217/nnm.16.5 |
| [42] |
LI J, WANG X, MEI K, et al. Lateral size of graphene oxide determines differential cellular uptake and cell death pathways in Kupffer cells, LSECs, and hepatocytes[J]. Nano Today, 2020, 37: 1-18. |
| [43] |
SYKES E A, QIN D, SARSONS C D, et al. Tailoring nanoparticle designs to target cancer based on tumor pathophysiology[J]. PNAS, 2016, 113(9): E1142-E1151. |
| [44] |
CHENG S H, LI F C, SOURIS J S, et al. Visualizing dynamics of sub-hepatic distribution of nanoparticles using intravital multiphoton fluorescence microscopy[J]. ACS Nano, 2012, 6(5): 4122-4131. DOI:10.1021/nn300558p |
| [45] |
FOROOZANDEH A, AZIZ A A. Insight into cellular uptake and intracellular trafficking of nanoparticles[J]. Nanoscale Research Letters, 2018, 13(339): 1-12. |
| [46] |
OUYANG B, POON W, ZHANG Y N, et al. The dose threshold for nanoparticle tumor delivery[J]. Nature Materials, 2020, 19: 1362-1371. DOI:10.1038/s41563-020-0755-z |
| [47] |
POON W, ZHANG Y N, OUYANG B, et al. Elimination pathways of nanoparticles[J]. ACS Nano, 2019, 13(5): 5785-5798. DOI:10.1021/acsnano.9b01383 |
| [48] |
PERRY J L, REUTER K G, KAI M P, et al. PEGylated PRINT nanoparticles: The impact of PEG density on protein binding, macrophage association, biodistribution, and pharmacokinetics[J]. Nano Letters, 2012, 12(10): 5304-5310. DOI:10.1021/nl302638g |




