螺旋管式换热器具有结构紧凑,耐压性能强,传热能力强等优点,广泛应用于石油化工、天然气、核工业、处理厂、余热回收系统、制冷、食品工业等工业领域。作为应用于大型石油化工工艺过程重要的单元设备,由于其结构复杂,螺旋管内流动机理及强化传热的研究还不太充分。因此,对螺旋管内部流动机理以及如何在压力损失允许范围内尽可能提高传热性能的研究具有较高的理论价值和实用价值。
螺旋管内垂直于主流方向平面内的二次流[1]远比普通直管要强,因此在无源强化传热技术中,螺旋管内混合强化传热具有重要意义,KUMAR [2]和ACHARYA [3]等人对其进行了研究。与直管相比,螺旋管内从层流到湍流发生转变时的临界雷诺数更高,ITO [4]、SCHMIDT [5]、SRINICASAN [6]、JANSSEN [7]等通过大量实验得到了在不同曲率比下螺旋管内对应临界雷诺数组成的曲线,其中ITO [4]和SCHIMIDT[5]研究得到的曲线几乎重合。ROGERS等[8]通过实验研究了被蒸汽加热的螺旋管内流体的流动传热性能。MORI等[9]对两种不同曲率的螺旋管恒定壁温条件下的对流传热进行了研究。YANG等[10]对使用标准k-ε模型对螺旋管中充分发展的湍流强迫对流传热进行了数值模拟研究。MOAWED [11]实验研究了不同结构参数对螺旋管强制对流传热的影响。PAWAR等[12]建立了3种不同的螺旋管,以层流下管内流动的大量数据为基础推导了努塞尔数Nu的关联式,创造性地提出了无量纲数“M”。ZACHÁR [13]研究了外波纹内肋的异形螺旋管的稳态强化传热问题,研究表明与普通螺旋管相比该管内传热系数提高了80%~100%,相对压降增加了10%~600%。
近年来提出的新型高效换热管大多应用于直管,前苏联学者ASMANTAS等[14]和DZYUBENKO等[15]对椭圆扭曲管束换热器进行了理论分析及实验研究。孟继安等[16]通过数值模拟的方法对椭圆扭曲直管内流动传热及流阻特性进行了理论分析和数值计算。杨胜等[17]采用计算流体力学软件对椭圆扭曲直管内的纵向涡流动特性及强化传热机理进行了研究。朱冬生等[18]、刘世杰等[19]通过实验和数值模拟研究了椭圆扭曲直管的传热及压降特性,并给出了计算关联式。高学农等[20]实验研究了高扭曲比的椭圆扭曲管内传热及压降性能,拟合了相应的计算准则关联式。马芳芳等[21]通过场协同原理研究了椭圆扭曲管强化传热和流动减阻性能的影响因素及机理。
如前所述,异形强化换热管换热器传热效率高、综合性能优异,已得到广泛应用。但目前与螺旋管式换热器有关的科学研究和工程应用大多采用的是圆管,对于异形螺旋管的报道不多,因此针对提高螺旋管式换热器传热效率的研究具有较高价值。本文结合椭圆扭曲管与螺旋管各自的优势,提出了一种新型的椭圆扭曲螺旋管,以水为介质,通过数值计算方法研究了椭圆扭曲螺旋管的流动传热和压降特性,并利用模拟结果拟合了椭圆扭曲螺旋管的计算关联式。
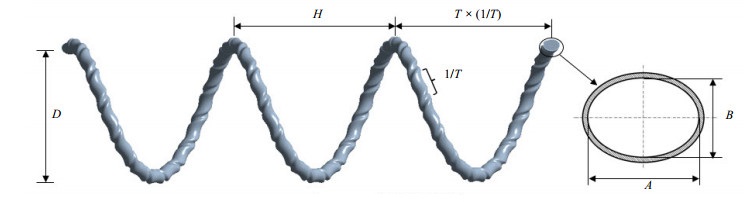
2 计算模型 2.1 物理模型及网格无关性验证建立14种不同的椭圆扭曲螺旋管(twisted ellipse helical coiled tube)几何模型,如图 1所示,并建立相应的椭圆螺旋管(ellipse helical coiled tube)和螺旋圆管(helical coiled tube)几何模型,具体结构尺寸见表 1。
|
图 1 椭圆扭曲螺旋管模型 Fig.1 Model of the twisted ellipse helical coiled tube |
|
|
表 1 换热管结构参数 Table 1 Structural parameters of tubes |
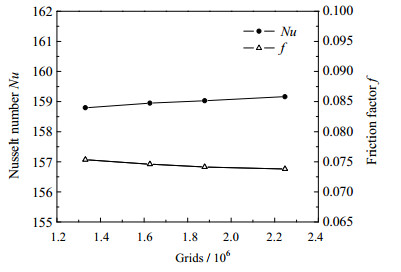
为尽可能减少网格数量、节省计算资源,首先对该换热管进行网格无关性验证。涉及的3种换热管在计算前均进行了网格无关性验证,以模型TEHCT 5为例进行说明,该模型建立了4套网格,网格数从133万到224万不等,在保证壁面温度相同的情况下入口流速均取2 m·s-1,经过计算得出的努塞尔数Nu和阻力系数f变化情况如图 2、表 2所示。网格(II)努塞尔数Nu的变化在1%左右,阻力系数f 的变化为0.13%,综合考虑计算精度和效率两个方面,本文选用网格(II)进行模拟计算。
|
图 2 网格无关性验证 Fig.2 Verification of grid-independency of numerical solution |
|
|
表 2 不同网格数计算结果比较 Table 2 Comparison of numerical simulation results of different cell cell numbers |
采用Fluent数值计算,以27 ℃的水为介质进行研究,入口速度设置为2~5 m·s-1,由于在相应的温度区间内水的物性随温度变化不大,物性参数可视为常量,壁面恒温且无滑移,采用表压为0的压力出口。控制方程均通过压力速度耦合SIMPLE算法和Realizable k-ε湍流模型进行求解计算,近壁区壁面函数采用Scalable Wall Function,在带有旋转或涡流的问题中,离散格式采用Third-Order MUSCL能提供更高的精度。
2.2 模型验证SCHMIDT [5]设计了空气和水分别在如表 3所示5种不同尺寸螺旋管中的无相变流动实验,管内介质的雷诺数Re在102~105,饱和蒸汽在管外冷凝以提供较为恒定的壁温。定义螺旋管内部临界雷诺数Recr:
|
|
表 3 Schmidt实验的螺旋管尺寸 Table 3 Size of HCT in Schmidt's experiment |
| $ R{e_{cr}} = {2_{}}300\left( {1 + 8.6{\delta ^{0.45}}} \right) $ | (1) |
| $ \delta = {{{d_i}} / D} $ | (2) |
其中di为螺旋管内径,D为螺旋直径。
通过该实验SCHMIDT [5]拟合了空气和水在螺旋管内无相变流动的计算关联式:
(1)
| $ Nu = 3.65 + 0.08\left( {1 + 0.8{\delta ^{0.9}}} \right)Re_{}^{^{\left( {0.5 + 0.2903{\delta ^{0.194}}} \right)}}P{r^{{1 / 3}}} $ | (3) |
| $ f = \left( {1 + 0.14{\delta ^{0.97}}R{e^{\left( {1 - 0.664{\delta ^{0.312}}} \right)}}} \right)\frac{{64}}{{Re}} $ | (4) |
(2)
| $ Nu = 0.023\left[ {1 + 14.8\left( {1 + \delta } \right){\delta ^{{1 / 3}}}} \right]Re_{}^{^{\left( {0.8 - 0.22{\delta ^{0.1}}} \right)}}P{r^{{1 / 3}}} $ | (5) |
| $ f = (1 + \frac{{{{28}^{}}800{\delta ^{0.62}}}}{{Re}})\frac{{{{0.316}^{}}4}}{{R{e^{0.25}}}} $ | (6) |
(3)
| $ Nu = 0.023\left[ {1 + 3.6\left( {1 - \delta } \right){\delta ^{0.8}}} \right]Re_{}^{0.8}P{r^{{1 / 3}}} $ | (7) |
| $ f = \left[ {1 + 0.0823\left( {1 + \delta } \right){\delta ^{0.58}}R{e^{0.25}}} \right]\frac{{{{0.316}^{}}4}}{{R{e^{0.25}}}} $ | (8) |
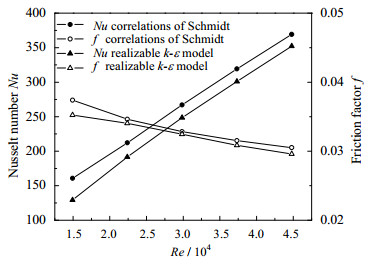
为了验证本模拟计算模型的可靠性,以恒壁温边界条件对内径7.5 mm的螺旋圆管流动传热及压降特性进行了数值模拟,并将结果与Schmidt经验关联式[5]进行比较,结果如图 3所示。图形表明该模型与经验关联式接近,由于本模拟和Schmidt实验[5]的换热元件尺寸不完全相同,努塞尔数Nu和阻力系数f的平均误差分别为9%和3%,说明该计算模型具有一定的可靠性。
|
图 3 努塞尔数Nu和阻力系数f与Schmidt经验公式对比 Fig.3 Comparison of Nu and f with Schmidt correlations |
27 ℃的水在椭圆扭曲螺旋管内流动,分析不同结构参数对换热管整体的平均传热系数及压降的影响。图 4为TEHCT内流线图,从短轴B上等间距取7个点,可以看到这7个点在管内的旋转运动十分剧烈,从而可以达到扰乱边界层,使边界层和主流区的混合程度加剧,从而增强传热效果。

|
图 4 椭圆扭曲螺旋管内流线图 Fig.4 Stream traces inside TEHCT |
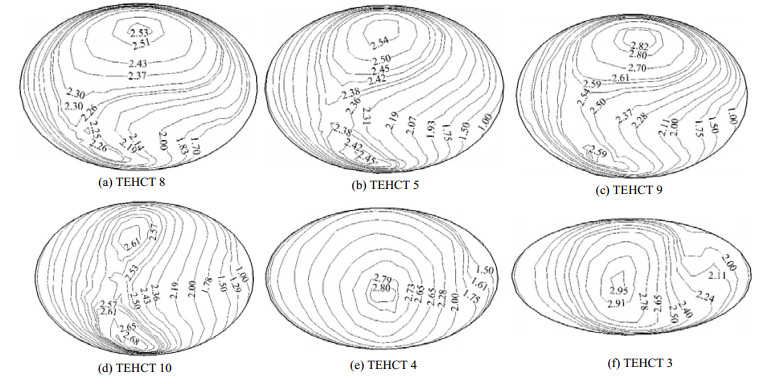
图 5为TEHCT 3、4、5、8、9、10在距离进口200 mm处截面合速度分布。从图中可以看出,4个截面合速度均产生不同程度的扭曲,说明流体通过扭曲壁面的作用力以及螺旋运动产生的离心力引起了不同程度的二次流。通过对比可以发现较小的长短轴比A/B和较大的扭曲数T更容易引起管内的二次流,从而扰乱边界层使对流换热过程更加强烈。
|
图 5 不同换热管横截面合速度分布 Fig.5 Velocity distributions at cross-section in different tubes |
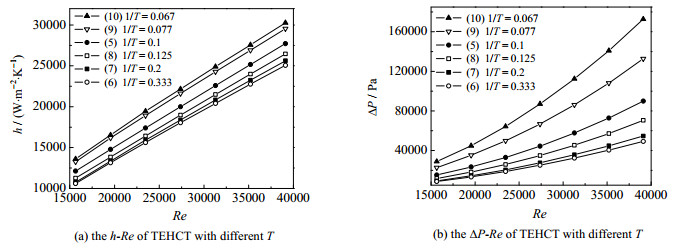
扭曲数T为螺旋管旋转一个周期中截面扭曲的圈数,该数大则TEHCT扭曲程度越强。从图 6中可以看出,相同的雷诺数Re下,扭曲数越大,则换热效果越好,同时压降ΔP也越大。扭曲数T从3增加到15时,管内传热系数h平均增大23.6%,管内压降ΔP平均增大243.2%。这是因为随着T的增加,管内流场的扭曲程度加剧,加速了边界层的分离与破坏,从而达到增加换热效果的目的,同时也加强了管内二次流程度,导致压降也急剧上升。
|
图 6 扭曲数T对椭圆扭曲螺旋管性能影响 Fig.6 Effects of T on the performance of TEHCT |
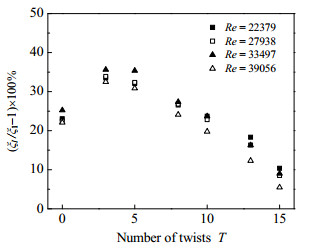
图 7为不同雷诺数Re下TEHCT与HCT等泵功综合性能评价因子ξ[22]之比随扭曲数T的变化情况。可以看出,在本文研究范围内TEHCT综合性能均优于HCT,相同雷诺数Re的情况下随着扭曲数T的增加,TEHCT的综合性能ξ降低,且扭曲数T大于8以后综合性能ξ不如EHCT。这是因为扭曲数T对压降的影响比对换热系数的影响更大,随着扭曲数T的增加,管内压降升高速度超过换热系数增大的速度,导致其综合性能ξ降低。
|
图 7 扭曲数T对综合性能ξ影响 Fig.7 Effects of T on the comprehensive performance of TEHCT |
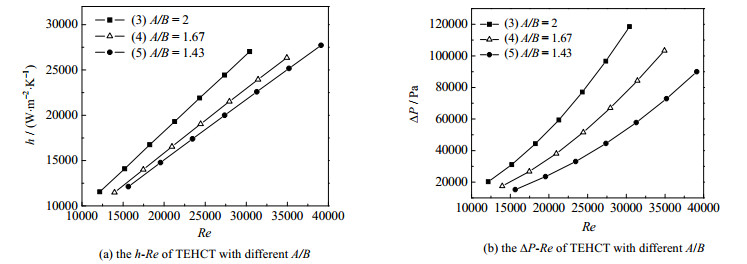
从图 8中曲线可以看出,相同雷诺数Re下,长短轴之比A/B越大,则管子的换热效果增强,同时压降ΔP也越大。在15 000 < Re < 32 000,TEHCT 4、3和5相比,传热系数h平均增加10.5%和36.1%,压降平均增加了57.8%和172.6%。这是因为A/B值越大,管子截面越趋于扁平,管内流场速度梯度增大,湍流程度增强,提高了换热效果的同时也导致了压降增大。
|
图 8 长短轴比A/B对椭圆扭曲螺旋管性能影响 Fig.8 Effects of A/B on the performance of TEHCT |
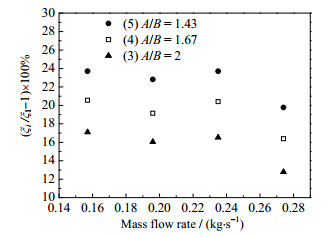
图 9为不同长短轴比A/B下TEHCT综合性能ξ随流量的变化情况。可以看出随着流量的增加其综合性能ξ没有明显变化,当流量增至0.274 kg·s-1时TEHCT综合性能ξ略微减小,这是因为流速增大到一定程度以后综合性能ξ对压降的敏感程度要高于换热系数。且可以看出,流量相同时TEHCT综合性能满足ξ5 ˃ ξ4 ˃ ξ3的关系,A/B从1.43增加到2时其综合性能下降了6.9%,因为A/B越大代表TEHCT截面越趋于扁平,管内压降增速高于传热系数增速,因此其综合性能ξ下降。
|
图 9 长短轴比A/B对综合性能ξ影响 Fig.9 Effects of A/B on the comprehensive performance of TEHCT |
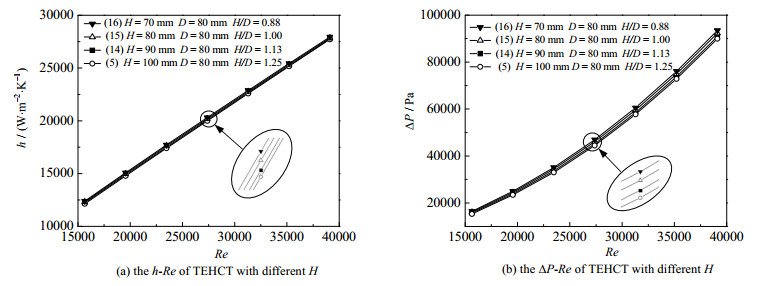
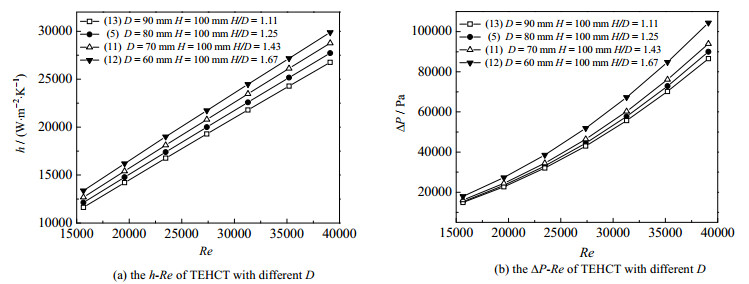
从图 10中可以看出,相同雷诺数Re下,随着螺距H增大,传热系数h和压降ΔP略微减小,当螺距H从70增加到100 mm,管内传热系数h平均变化在1.5%内,压降ΔP平均变化在5.6%内。从图 11中可以看出,相同雷诺数Re下,随着螺旋直径D增大,传热系数h和压降ΔP越小,当螺旋直径D从60增加到90 mm,管内膜传热系数h平均减少11.5%,压降ΔP平均减少17.1%。从上述结果对比可以发现螺距H对传热系数和压降的影响不如螺旋直径D的影响明显,这是因为螺旋直径D的改变对管子曲率影响比螺距H大,管子曲率会直接影响管内二次流的强弱,曲率越大则二次流程度越强,传热系数越高,压降也越大。
|
图 10 螺距H对椭圆扭曲螺旋管性能影响 Fig.10 Effects of H on the performance of TEHCT |
|
图 11 螺旋直径D对椭圆扭曲螺旋管性能影响 Fig.11 Effects of D on the performance of TEHCT |
通过数值模拟方法研究了椭圆扭曲螺旋管内流动传热和压降特性与扭曲数T、长短轴比A/B、螺距H、螺旋直径D以及雷诺数Re之间的关系。采用多元线性回归方法对模拟结果进行拟合得到以下计算准则关联式:
| $ Nu = 2.{\rm{59}}R{e^{0.{\rm{907}}}}P{r^{{\rm{ - 2}}{\rm{.18}}}}{\left( {\frac{{A + B}}{D}} \right)^{0.{\rm{274}}}}{\left( {\frac{{A + B}}{H}} \right)^{0.{\rm{011}}}}{\left( {\frac{A}{B}} \right)^{ - 0.{\rm{142}}}}{\left( {\frac{1}{T}} \right)^{ - 0.{\rm{126}}}} $ | (9) |
| $ f = {\rm{1}}{\rm{.942}}R{e^{ - 0.{\rm{1365}}}}{\left( {\frac{{A + B}}{D}} \right)^{{\rm{1}}{\rm{.49}}}}{\left( {\frac{{A + B}}{H}} \right)^{0.0{\rm{38}}}}{\left( {\frac{A}{B}} \right)^{0.{\rm{229}}}}{\left( {\frac{1}{T}} \right)^{ - {\rm{0}}{\rm{.66}}}} $ | (10) |
适用范围:
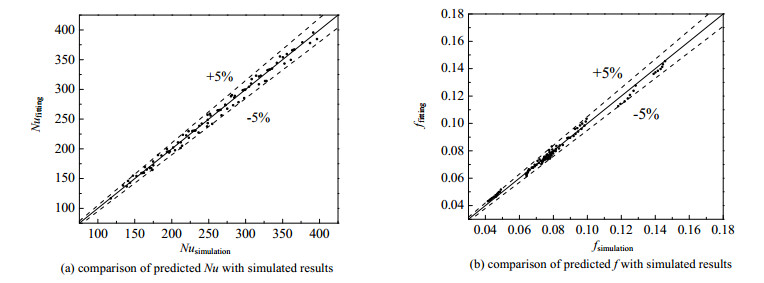
图 12为模拟结果和拟合值对比,在本文研究范围内,拟合得到的管内努塞尔数Nu关联式与模拟得到的结果平均偏差为1.81%,最大偏差为5.31%;拟合得到的管内阻力系数f关联式与模拟得到的结果平均偏差为1.98%,最大偏差为5.15%,说明本文拟合的计算准则关联式与数值模拟结果有较高的吻合度。
|
图 12 关联式预测努塞尔数Nu和阻力系数f与模拟结果对比 Fig.12 Comparison of predicted Nu and f with simulated results |
通过数值模拟的方法研究了不同工况下本文提出的椭圆扭曲螺旋管的单一结构参数对传热效果和压降的影响,得到以下结论:
(1) 与螺旋圆管相比,椭圆扭曲螺旋管具有更强的传热性能,传热效果随着扭曲数T、长短轴比A/B的增大及螺旋直径D、螺距H的减小而增强,同时压降也相应增大,螺距H的变化对传热效果和压降影响较小。
(2) 在相同流量条件下,椭圆扭曲螺旋管的综合性能随着扭曲数T以及长短轴比A/B的增大而减小,且综合性能均强于螺旋圆管。
(3) 由模拟计算结果,通过多元线性回归获得了椭圆扭曲螺旋管流动传热和压降计算关联式,为后续相关椭圆扭曲螺旋管的研究提供参考。
符号说明:
|
|
| [1] |
DEAN W R. XVI. Notes on the motion of fluid in a curved pipe[J]. Philosophical Magazine, 1927, 4(20): 208-223. |
| [2] |
KUMAR V, Nigam K D P. Numerical simulation of steady flow fields in coiled flow inverter[J]. International Journal of Heat and Mass Transfer, 2005, 48(23): 4811-4828. |
| [3] |
ACHARYA N, SEN M, CHANG H C. Analysis of heat transfer enhancement in coiled-tube heat exchangers[J]. International Journal of Heat and Mass Transfer, 2001, 44(17): 3189-3199. DOI:10.1016/S0017-9310(01)00002-3 |
| [4] |
ITO H. Friction factors for turbulent flow in curved pipes[J]. Journal of Basic Engineering, 1959, 81(2): 123-134. DOI:10.1115/1.4008390 |
| [5] |
SCHMIDT E F. Wärmeübergang und druckverlust in rohrschlangen[J]. Chemie Ingenieur Technik, 1967, 39(13): 781-789. DOI:10.1002/cite.330391302 |
| [6] |
SRINIVASAN P S, NANDAPURKAR S S, HOLLAND F A. Friction factor for coils[J]. Transactions of the Institution of Chemical Engineer, 1970, 48(6): 156-161. |
| [7] |
JANSSEN L A M, HOOGENDOORN C J. Laminar convective heat transfer in helical coiled tubes[J]. International Journal of Heat and Mass Transfer, 1978, 21(9): 1197-1206. DOI:10.1016/0017-9310(78)90138-2 |
| [8] |
ROGERS G F C, MAYHEW Y R. Heat transfer and pressure loss in helically coiled tube with turbulent flow[J]. International Journal of Heat and Mass Transfer, 1964, 7(11): 1207-1216. DOI:10.1016/0017-9310(64)90062-6 |
| [9] |
MORI Y, NAKAYAMA W. Study of forced convective heat transfer in curved pipes[J]. International Journal of Heat and Mass Transfer, 1967, 10(1): 37-59. |
| [10] |
YANG G, EBADIAN M A. Turbulent forced convection in a helicoidal pipe with substantial pitch[J]. International Journal of Heat and Mass Transfer, 1996, 39(10): 2015-2032. DOI:10.1016/0017-9310(95)00303-7 |
| [11] |
MOAWED M. Experimental study of forced convection from helical coiled tubes with different parameters[J]. Energy Conversion and Management, 2011, 52(2): 1150-1156. DOI:10.1016/j.enconman.2010.09.009 |
| [12] |
PAWAR S S, SUNNAPWAR V K. Studies on convective heat transfer through helical coils[J]. Heat and Mass Transfer, 2013, 49(12): 1741-1754. DOI:10.1007/s00231-013-1210-3 |
| [13] |
ZACHÁR A. Analysis of coiled-tube heat exchangers to improve heat transfer rate with spirally corrugated wall[J]. International Journal of Heat and Mass Transfer, 2010, 53(19): 3928-3939. |
| [14] |
ASMANTAS L A, NEMIRA M A, TRILIKAUSKAS V V. Coefficients of heat transfer and hydraulic drag of a twisted oval tube[J]. Heat Transfer-Soviet Research, 1985, 17(4): 103-109. |
| [15] |
DZYUBENKO B V, ASHMANTAS L A, SEGAL M D. Unsteady heat and mass transfer in a heat exchanger with twisted tubes[J]. Power Engineering, 1985, 23(4): 102-110. |
| [16] |
孟继安, 李志信, 过增元, 等. 螺旋扭曲椭圆管层流换热与流阻特性模拟分析[J]. 工程热物理学报, 2002, 23(s1): 117-120. MENG J A, LI Z X, GUO Z Y, et al. Simulation and analysis on laminar flow and heat transfer in twisted ellipse-tube[J]. Journal of Engineering Thermophysics, 2002, 23(s1): 117-120. |
| [17] |
杨胜, 张莉, 胡腾, 等. 螺旋扭曲椭圆管内纵向涡流动特性与强化传热机理的CFD分析[J]. 制冷技术, 2014, 42(10): 73-78. YANG S, ZHANG L, HU T, et al. CFD analysis on longitudinal vortex flow characteristics and heat transfer enhancement mechanism of a spiral twisted elliptical tube[J]. Refrigeration, 2014, 42(10): 73-78. |
| [18] |
朱冬生, 石仲璟, 钱泰磊, 等. 扭曲椭圆管换热器的数值模拟及场协同分析[J]. 高校化学工程学报, 2015, 29(1): 64-71. ZHU D S, SHI Z J, QIAN T L, et al. Numerical simulation and field synergy analysis of a twisted elliptical tube heat exchanger[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(1): 64-71. DOI:10.3969/j.issn.1003-9015.2015.01.009 |
| [19] |
刘世杰, 朱冬生, 张洁娜, 等. 三维变形管MVR蒸发器的强化传热数值研究[J]. 高校化学工程学报, 2018, 32(6): 1307-1313. LIU S J, ZHU D S, ZHANG J N, et al. Numerical study on heat transfer enhancement of MVR evaporator with 3D-deformation tube[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(6): 1307-1313. DOI:10.3969/j.issn.1003-9015.2018.06.009 |
| [20] |
高学农, 邹华春, 王端阳, 等. 高扭曲比螺旋扁管的管内传热及流阻性能[J]. 华南理工大学学报, 2008, 36(11): 17-26. GAO X N, ZOU H C, WANG D Y, et al. Heat transfer and flow resistance properties in twisted oblate with large twist ratio[J]. Journal of South China University of Technology, 2008, 36(11): 17-26. DOI:10.3321/j.issn:1000-565X.2008.11.004 |
| [21] |
马芳芳, 云和明, 郭训虎, 等. 扭曲椭圆管强化换热与流动减阻特性的场协同分析[J]. 高校化学工程学报, 2017, 31(6): 1301-1311. MA F F, YUN H M, GUO X H, et al. Field synergy analysis on heat transfer enhancement and flow drag reduction characteristics in twisted oval tubes[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(6): 1301-1311. |
| [22] |
WEBB R L. Principles of enhanced heat transfer[M]. New York: John Wiley & Son, 1995.
|




