2. 数字社区教育部工程研究中心, 北京 100124;
3. 城市轨道交通北京实验室, 北京 100124;
4. 计算智能与智能系统北京市重点实验室, 北京 100124;
5. 内蒙古工业大学 电力学院, 内蒙古 呼和浩特 010051
2. Engineering Research Center of Digital Community, Ministry of Education, Beijing 100124, China;
3. Beijing Laboratory for Urban Mass Transit, Beijing 100124, China;
4. Beijing Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China;
5. School of Electric Power, Inner Mongolia University of Technology, Hohhot 010051, China
间歇过程是指在有限的时间内将原材料制成小批量和高附加值的目标产品。间歇过程作为一种重要的工业生产方式,在现代制造业中发挥着不可或缺的作用[1]。典型的间歇过程包括食品[2]、药品[3]和聚合物[4]。这些产品在人们的日常生活中起着重要作用。为了确保安全、可持续和有效益的生产,间歇过程建模和监测一直受到高度关注[5-9]。
多阶段特性是间歇过程中的典型特性,但目前常见的数据驱动方法往往进行全局建模,忽略多阶段特性,不能准确提取局部特征[10-13]。在间歇过程多阶段故障监测方法中,关键问题是如何实现有效的阶段划分以及如何建立准确的局部模型。很多阶段划分方法都沿用了聚类算法。随着聚类理论的发展,基于划分的聚类算法由于复杂度较低,常常需要加以改进和应用。Lu等[14]使用K均值聚类进行阶段划分,他们利用每个时间片的聚类权重来划分阶段,然而K均值聚类作为一种硬化分算法,一个样本只能隶属于一种聚类,这种聚类算法严格界定划分类别,导致较大的划分误差。Bezdek等[15]提出的模糊C均值(fuzzy C-means, FCM)算法是一种融合模糊理论的软划分算法。该算法隶属度在0到1的区间内,弥补了硬化分聚类的缺陷。然而,传统的FCM算法还存在一些不足:1)聚类个数需要人为确定;2)不能表征样本之间的相关性;3)对离群点敏感,抗噪性能差,易收敛到局部最优。因此,Verma等[16]利用直觉模糊算法改进隶属度函数,强化样本之间的相关性,改善了划分效果,但该方法对噪声仍旧敏感,且容易造成局部最优。Khalilia等[17]提出的关系模糊C均值算法,将相异度矩阵欧式化,真实表征因噪声导致的聚类失真的量,弱化了噪声对数据划分的影响。Wu等[18]在FCM算法中引入自适应权重和自适应指数,对初始聚类中心进行优化,避免了局部最优。以上方法虽然一定程度上对原始FCM算法进行了改进,但仍旧是利用欧式距离线性地表征2个样本点之间的相关性,忽略了数据之间的局部密度,未能表征样本的非线性。而在处理非线性问题上,Wang等[19]利用主成分分析方法(principal component analysis,PCA)压缩隐空间再构建多层极限学习机网络来堆叠压缩的隐空间,虽然可以有效处理非线性问题,但是在堆叠过程中不可避免地要增加隐节点进行多层堆叠,增加网络结构复杂性,降低算法的计算效率。扩散距离来自由Coifman和Lafon提出的扩散图[20-21],但常见的扩散图常用于降维,这限制了它的应用[22]。Tang等[23]利用扩散距离定义了重复度因子来测量每批间歇数据之间的重复性,但未对每个子阶段进行局部度量。
针对上述问题,本研究提出一种基于扩散距离的信息熵模糊C均值(diffusion distance and entropy fuzzy C-means,DDEFCM) 多阶段长短期记忆网络的自动编码器(long short-term memory-autoencoder,LSTM-AE)[24]间歇过程故障监测方法。主要贡献如下:1)在FCM算法中引入信息熵,解决FCM人为确定聚类个数的缺陷;2)利用扩散距离对FCM进行改进,并引入基于扩散距离的轮廓系数[25](silhouette coefficient)划分过渡阶段,评估划分性能;3)分别建立LSTM-AE故障监测的阶段子模型,有效适应所有阶段的数据分布特性,提高监测精度。
2 基本方法 2.1 模糊C均值算法FCM算法作为一种软划分聚类算法,隶属度的值在0到1区间,该算法根据每个时间片的最大隶属度进行分类,将相似度最大的划分成一类。定义FCM算法的公式如式(1)~(4)所示。其中,n是样本个数,c是阶段划分的聚类数,m是模糊系数,U是由uij构成的c×n的模糊划分矩阵,uij是第j个样本xj属于第i簇的隶属度值,其中
| $ J( \boldsymbol{U}, v) = \mathop \sum \limits_{i = 1}^c \mathop \sum \limits_{j = 1}^n \mu _{ij}^md_{ij}^2 = \mathop \sum \limits_{i = 1}^c \mathop \sum \limits_{j = 1}^n \mu _{ij}^m||{x_j} - {v_i}|{|^2} $ | (1) |
| $ {d_{ij}} = ||{x_j} - {v_i}|| $ | (2) |
| $ {v}_{i}=\frac{\sum\limits_{j=1}^{n}{u}_{ij}^{m}{x}_{j}}{\sum\limits_{j=1}^{n}{u}_{ij}^{m}}, i=1, 2, \cdots , c $ | (3) |
| $ {u_{ij}} = \left\{ {\begin{array}{*{20}{l}} {{{\left[ {\sum\limits_{r = 1}^c {{{\left( {\frac{{{d_{ij}}}}{{{d_{rj}}}}} \right)}^{\frac{2}{{m - 1}}}}} } \right]}^{ - 1}}{\rm{,}}{I_j} = \varnothing }\\ {\frac{1}{{\left| {{I_j}} \right|}},{I_j} \ne \varnothing ,i \in {I_j}}\\ {0,{I_j} \ne \varnothing ,i \notin {I_j}} \end{array}} \right. $ | (4) |
FCM算法如下:
1) 确定聚类数c,模糊系数m,并对各簇中心vi初始化;
2) 根据式(4)求取U(k+1);
3) 根据式(3)求取V(k+1),并设k=k+1;
4) 迭代上述步骤2)和3),当
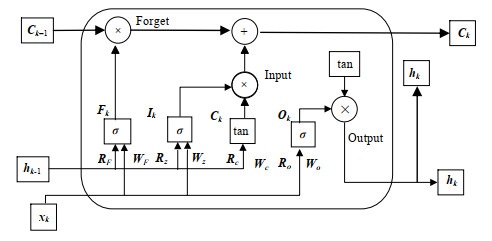
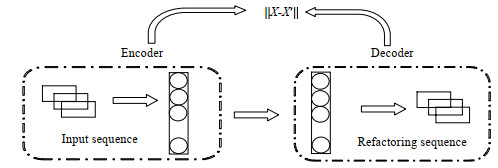
在深度学习中,自动编码器(auto-encoder,AE)[26]通常由编码器和解码器组成。由于AE容易忽略数据间的时序动态性。Hochreiter等[27]提出的长短期记忆网络(long short-term memory,LSTM)能够灵活处理长短期时间序列的动态特性。LSTM结构如图 1所示,通过遗忘门、输入门、输出门对长短期序列进行不同程度的记忆。通过添加LSTM单元来扩充传统AE,构建LSTM-AE网络。具体结构图如图 2所示。Ck−1和hk−1分别表示k−1时刻的细胞输出信息和隐层信息,Ck和hk表示k时刻的细胞输出信息和隐层信息,Ok表示输出门信息,Fk表示当前k时刻遗忘门信息,Ik表示k时刻输入门信息。xk表示k时刻网络的输入样本,WF、WI和 WO分别表示遗忘门、输入门和输出门特征提取时hk−1的权重矩阵。WC表示当前时刻细胞内部状态对应的权重矩阵。RF、RI、和RO分别表示遗忘门、输入门和输出门特征提取时xk的权重矩阵。RC表示前一时刻细胞内部状态对应的权重矩阵。σ表示任意某个激活函数,输入门决定k时刻输入对当前时刻单元状态的更新程度,计算激活函数tanh,得到当前时刻单元状态的候选值。输出门决定了k−1时刻单元状态对k时刻隐层hk的影响。
|
图 1 长短期时间记忆网络单元结构 Fig.1 LSTM structure cell |
|
图 2 LSTM自动编码器结构 Fig.2 Structure of LSTM autoencoder |
该网络主要通过重构输入序列获得最小重构误差网络训练。其输出计算方式与误差重构公式如式(5)~(7)所示,其中X为原始样本矩阵;f(X)为编码器在k时刻的输出序列;Way为编码器的权值矩阵,下标a表示权值矩阵的行数,下标y表示权值矩阵的列数;by为编码器的偏置矩阵,该矩阵可由随机初始化进行配置;X′为解码器作用下的重构序列,令X′=g(f(X))。g(f(X))为解码器作用下的重构序列。
| $ f( \boldsymbol{X}) = {\boldsymbol{W}_{ay}}{\boldsymbol{h}_k} + {\boldsymbol{b}_y} $ | (5) |
| $ \min E = \min \{ E(\boldsymbol{X}, g(f(\boldsymbol{X})))\} $ | (6) |
然后利用重构误差E来求取原始样本和重构样本之间的重构差异。如式(7)所示,g(f(xk))为第k个时刻的重构样本。当重构误差最小时,达到模型训练要求。
| $ E = \frac{1}{2}\mathop \sum \limits_{k = 1}^t {\left( {\parallel {x_k} - g(f({x_k}){\parallel _{}}} \right)^2} $ | (7) |
间歇过程数据具有多阶段、非线性、动态性等特点。忽略间歇过程的多阶段特性会导致在全局建模过程中容易损失过渡过程信息,影响故障监测精度。在阶段划分中提取样本间的非线性特征可以提升阶段划分性能,提升监测精度。因此,本研究将信息熵和扩散距离引入FCM算法。
信息熵算法如式(8)和(9)所示。式(8)中,
| $ {H_i}(u) = \mathop \sum \limits_{j = 1}^n {H_{ij}}(u) $ | (8) |
| $ {H_{ij}}(u) = \mathop \sum \limits_{i = 1}^c {u_{ij}}{\log _2}{u_{ij}} $ | (9) |
获得聚类个数后,代入式(1)求FCM的目标函数,但由式(2)可知,传统欧式距离统一对簇内和簇间的所有样本点进行线性处理,忽略了数据之间的局部密度分布,导致在聚类过程中会多次迭代初始化聚类中心,误划分较为严重。因此本研究将原始表征2个任意时间片的扩散距离改进成能够表征每个时间片与信息熵确定的聚类中心的距离,然后将改进的扩散距离融入FCM算法中,从而更好地对间歇过程的非线性时间片矩阵进行阶段划分。
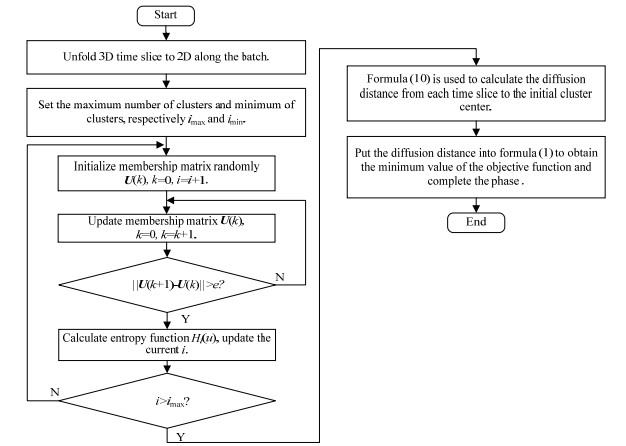
改进后扩散距离如式(10)所示。其中,s是X和pt (xj, ·)之间的任何样本,p是在从节点xj到聚类中心vi的转移概率,它可以表示任意节点到聚类中心vi的所有路径的概率,p如式(11)所示。其中,kβ是宽度为β的高斯核,它是对非线性数据进行分割的重要参数。kβ如式(12)所示。其中β是核宽度。每个点x的度数给出如式(13)所示。其中,q(s)为相应的平稳分布函数,计算如式(14)所示。计算出每个时间片距离聚类中心的扩散距离D后,将扩散距离与之前计算得到的聚类个数分别代入式(1),求取目标函数,当该函数值最小时,聚类算法结束,完成阶段划分。DDEFCM算法流程如图 3所示。
|
图 3 DDEFCM算法流程图 Fig.3 Flow chart of DDEFCM algorithm |
| $ {D^2}\left( {{x_j}, {v_i}} \right) = \parallel {p_t}\left( {{x_j}, \cdot } \right) - {p_t}\left( {{v_i}, \cdot } \right)\parallel _{1/q}^2 = \mathop \sum \limits_{s \in X} \frac{{{{\left( {{p_t}\left( {{x_j}, s} \right) - {p_t}\left( {{v_i}, s} \right)} \right)}^2}}}{{q(s)}} $ | (10) |
| $ p\left( {{x_j}, {v_i}} \right) = \frac{{{k_\beta }\left( {{x_j}, {v_i}} \right)}}{{{{\deg }_{}}\left( {{x_j}} \right)}} $ | (11) |
| $ {k_\beta } = {\exp _{}}\left( { - \frac{{\parallel {x_j} - {v_i}{\parallel ^2}}}{{2\beta }}} \right) $ | (12) |
| $ {\deg _{}}\left( {{x_j}} \right) = \mathop \sum \limits_{s \in X} {k_\beta }\left( {{x_j}, s} \right) $ | (13) |
| $ q(s) = \frac{{{{\deg }_{}}(s)}}{{\mathop \sum \nolimits_{s \in X} {{\deg }_{}}(s)}} $ | (14) |
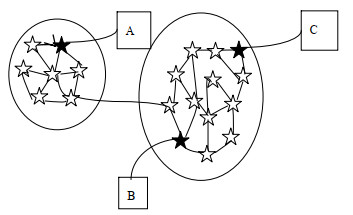
进一步对DDEFCM优越性进行解释,假设有2个独立的数据点集群(见图 4)。如果按基于欧式距离的FCM算法进行数据划分,B点和A点(簇间)之间的欧式距离与B点和C点(簇内)之间的距离相似,此时,A点、B点、C点应该处于同一簇。但由于它们的连通性非常不同,从B点到C点的随机路径远大于从B点到A点,按基于扩散距离的FCM算法,则只有B点和C点处于同一簇。这导致扩散距离和欧氏距离的差异。因此,衡量阶段划分的准确性,不仅取决于点之间的相似性,还取决于局部密度分布。这也是为何基于欧式距离的FCM抗噪能力差,不能表征样本非线性的原因。
|
图 4 T步随机游走扩散图 Fig.4 Diffusion graph of T-step random walk |
利用上述方法对批处理后的时间片矩阵进行阶段划分,解决间歇过程因忽略非线性导致阶段划分准确率低的问题后,往往需要初步验证划分性能。轮廓系数(Silhouette)常常被用来验证聚类划分的准确性。如式(15)所示,A(x)表示样本x到所有它属于的簇内其他点的距离。B(x)表示样本x到某一不包含它的簇中所有点的平均距离,Sil(x)表示每个样本的轮廓系数值。当Sil(x)与1相近,则样本x划分合理,当Sil(x)与−1相近,则样本x应划分到其他簇。
| $ \text{Sil}(x) = \left\{ \begin{gathered} 1 - \frac{{A(x)}}{{B(x)}}, \;\;\;A(x) < B(x) \hfill \\ 0, \;\;\;\;\;\;\;\;\;\;\;\;A(x) = B(x) \hfill \\ \frac{{B(x)}}{{A(x)}} - 1, \;\;\;A(x) > B(x) \hfill \\ \end{gathered} \right. $ | (15) |
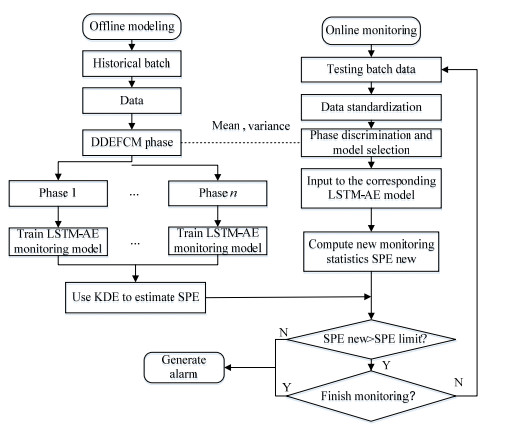
间歇过程阶段划分结束后,为了验证本研究提出的DDEFCM算法是否提升间歇过程故障监测性能,需要对阶段划分的数据进行故障监测。结合AE的编码解码优势以及LSTM处理长期时间序列的优势,本研究使用LSTM-AE网络来提高故障监测性能。同时,结合间歇过程数据的多阶段特性,本研究构建子阶段LSTM-AE模型进行故障监测。该模型由LSTM编码器和LSTM解码器2个模块组成。LSTM编码器主要用于接收输入序列,实现特征提取和特征压缩。LSTM解码器主要用于学习潜在向量与实际输出值之间的映射关系,并最终输出预测结果。在工业过程中,平方预测误差(squared prediction error,SPE)和霍特林(Hotelling,T2)统计量是2个常见的统计指标[29-30]。本研究基于LSTM-AE模型对每个子阶段重构原始特征,利用重构误差构建SPE统计指标,并利用核密度估计(kernel density estimation,KDE)[31]计算每个阶段正常样本SPE的控制限。具体监测流程如图 5所示。
|
图 5 LSTM-AE监测流程图 Fig.5 Flow chart of LSTM-AE monitoring |
1) 采集历史批次数据,对该数据沿批次展开,并按列进行标准化;
2) 采用DDEFCM算法对批处理后的时间片数据进行阶段划分,区分出稳定阶段和过渡阶段;
3) 将多批间歇过程正常工况数据输入LSTM-AE模型中,对该模型进行训练,根据模型重构误差计算得到正常样本的SPE统计量。计算如式(16)所示,其中,X=(x1, x2, …xn)T,L=(l1, l2, …ln)T。xn为第n个时刻输入的样本,L为重构样本矩阵,ln 为第n个时刻的重构样本。
| $ \text{SPE} = {( \boldsymbol{X} - \boldsymbol{L})^T}( \boldsymbol{X} - \boldsymbol{L}) $ | (16) |
4) 利用KDE算法计算每个阶段SPE对应的控制限。如式(17)所示,其中,spek为第k个正常样本的统计量值,G为核函数,f(speτ)为第τ个正常样本统计量。
| $ f(\text{spe}_{\tau })=\frac{1}{n\beta }\sum\limits_{\begin{array}{l}k=1\\ k\ne \tau \end{array}}^{n}G\left(\frac{\text{spe}_{\tau }-\text{spe}_{k}}{\beta }\right) $ | (17) |
5) 故障样本作为测试样本,利用DDEFCM算法进行阶段划分后,再代入对应的子阶段LSTM-AE监测模型中进行监测,计算测试集中每个样本的SPE;
6) 将测试样本的SPE与步骤4)中的正常样本控制限比较,若超出控制限,则故障报警。
5 实验验证 5.1 青霉素仿真平台实验青霉素(penicillin)是一种临床价值十分广泛的抗生素。作者使用Birol等[32]开发的青霉素发酵基准仿真平台Pensim2.0进行在线监控仿真研究。每批发酵数据生产时间为400 h,采样间隔为1 h,即一小时采样一次,样本总数为采样总时间。每个批次的初始条件均在允许的范围内稍加改变。研究利用40批次正常工况数据,选取10个过程变量进行建模和监控,过程变量如表 1所示,表中Z1~Z10为过程变量。为较好模拟实际生产状况,对训练样本加入一定量的高斯噪声干扰。
|
|
表 1 青霉素仿真平台过程变量 Table 1 Process variables of the penicillin simulation platform |
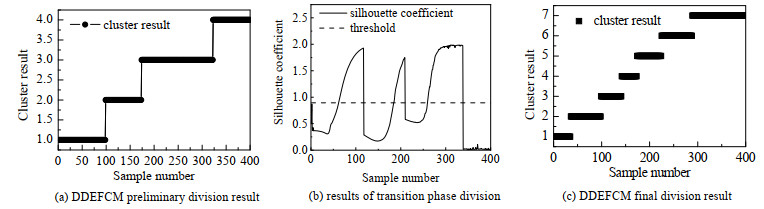
利用DDEFCM算法进行初步阶段划分,结果如图 6(a)所示。此时该算法将青霉素发酵过程初步划分成4个采样阶段,分别是1~98、99~173、174~322和323~400。再将每个阶段对应的扩散距离和聚类标签数据分别代入Silhouette系数公式,根据斜率大小分割出每2个阶段对应的过渡阶段,过渡阶段划分作图如图 6(b)所示,可以看出从第1个阶段在第36个采样时刻开始进入第1个过渡阶段,到第98个采样时刻结束。第2个阶段在第141个采样时刻进入第2个过渡阶段,到第173个采样时刻结束,第3个阶段在第224个采样时刻进入第3个过渡阶段,到第288个采样时刻结束。在第4个阶段无过渡过程。但从第3个阶段可以看到第289个采样时刻已经进入下1个稳定阶段,但是此时稳定阶段的Silhouette系数超过稳定阶段的阈值0.9475。所以在288~322阶段出现误划分。对误划分点进行阶段归属后,最终阶段划分结果如图 6(c)所示。可见稳定阶段为1~35、99~141、174~224和289~400。过渡阶段为36~98、142~173和225~288。
|
图 6 青霉素发酵过程DDEFCM阶段划分结果图 Fig.6 DDEFCM phase division results of penicillin fermentation process |
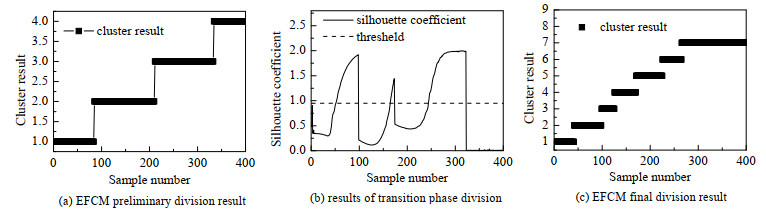
将本研究提出的DDEFCM算法与未改进的FCM算法、基于信息熵的模糊C均值(EFCM)算法作对比,验证本研究所提出算法的性能。EFCM进行初步阶段划分的结果如图 7(a)所示,EFCM算法将青霉素发酵过程数据初步划分成4个阶段,分别是1~117、118~209、210~338和339~400。将每个阶段对应的欧式距离和聚类标签分别代入Silhouette系数公式,分割过渡阶段,如图 7(b)所示,可知,在初始划分的第3个阶段出现误划分现象,超出稳定阶段阈值0.93。所以在第278~338阶段出现误划分。
|
图 7 青霉素发酵过程EFCM阶段划分结果图 Fig.7 EFCM phase division results of penicillin fermentation process |
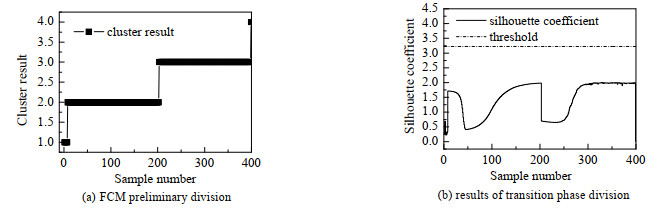
FCM进行初步阶段划分的结果如图 8(a)所示。此时FCM算法将青霉素发酵过程数据初步划分为4个阶段,分别是1~7、8~202、203~398和399~400。将每个阶段的欧式距离和聚类标签分别代入Silhouette系数公式,如图 8(b)所示,FCM进行阶段划分时,在第2个阶段无稳定阶段到过渡阶段的过渡,直接误判为过渡阶段,所以在8~150阶段出现误划分,误划分现象较为严重。
|
图 8 青霉素发酵过程FCM阶段划分结果图 Fig.8 FCM phase division results of penicillin fermentation process |
对比FCM、EFCM、DDEFCM的迭代次数、耗时以及划分准确率见表 2,由表 2可知,本研究提出的DDEFCM算法迭代次数最少,说明扩散距离不以迭代计算初始聚类中心为代价,且扩散距离对非线性数据的表征,更能突出利用该算法处理间歇过程多阶段特性时的优势。DDEFCM划分准确率为91.3%,虽然耗时2.87 s,但所耗时间仍在可接受的范围内。为验证所提方法在故障监测上的性能,如表 3所示,本研究选取了3组故障批次样本进行测试。
|
|
表 2 聚类算法在准确率上的比较 Table 2 Accuracy comparison of clustering algorithm |
|
|
表 3 青霉素发酵过程故障类型 Table 3 Fault types of penicillin fermentation process |
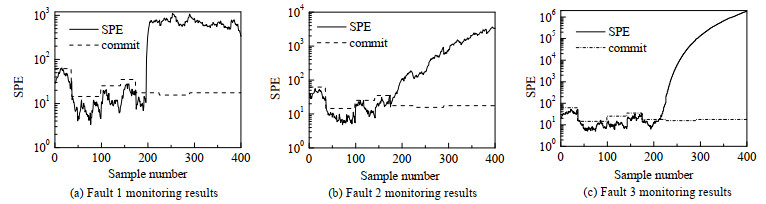
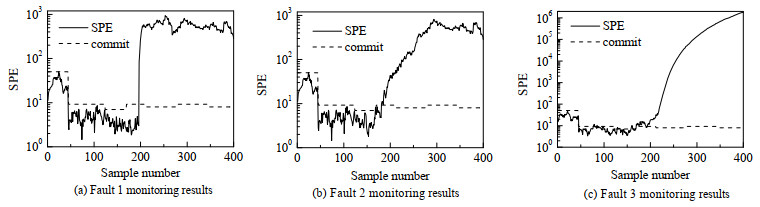
阶段划分结束后,采用LSTM-AE对间歇过程进行故障监测。将所提出的方法与EFCM-LSTM-AE故障监测模型、sub-DPCA监测模型和AE监测模型这3种情况对比。图 9、10为DDEFCM-LSTM-AE和EFCM-LSTM-AE对3种故障的监测图。黑色虚线是控制限,超出控制限,则立即报警。可以看出,对故障1而言,所提方法和EFCM-LSTM-AE均在故障发生后立即报警。但对故障2而言,EFCM- LSTM-AE在采样开始不久,就连续报警。这2种方法的故障检测率和误报率如表 4和5所示,表明本研究所提出方法可以大大减少误警率,提高故障监测性能。
|
图 9 青霉素发酵过程DDEFCM-LSTM-AE故障监测结果 Fig.9 DDEFCM-LSTM-AE fault monitoring in penicillin fermentation process |
|
图 10 青霉素发酵过程EFCM-LSTM-AE故障监测结果 Fig.10 EFCM-LSTM-AE fault monitoring in penicillin fermentation process |
|
|
表 4 2种距离的故障检测率对比 Table 4 Comparison of fault detection rates at two distances |
|
|
表 5 2种距离的故障误警率对比 Table 5 Comparison of fault alarm rates at two distances |
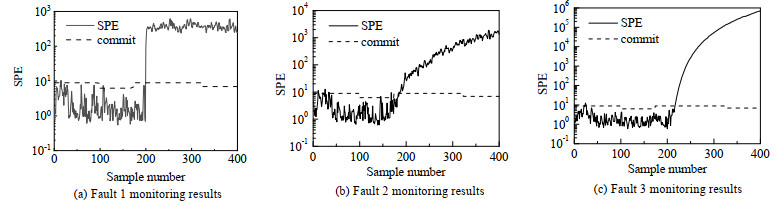
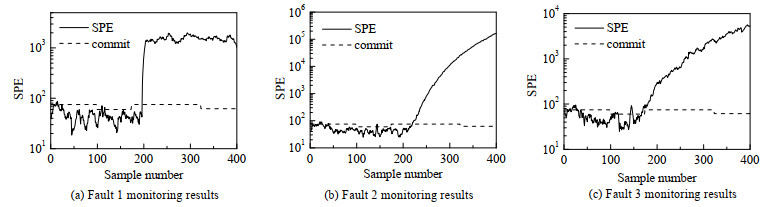
为了验证所提出方法在整个阶段划分算法上的有效性和准确性,将DDEFCM-LSTM-AE算法和只进行初步稳定阶段划分的传统AE方法、sub-DPCA方法进行对比,对比实验如图 9、11和12所示。可知,传统AE算法和sub-DPCA在故障1,2,3上采样开始不久都存在大量的误报现象。如表 6和7所示,所提方法对阶段划分进行非线性处理,误报率最低,故障检测率最高,监测性能最好。
|
图 11 青霉素发酵过程稳定阶段DDEFCM-AE监测结果 Fig.11 DDEFCM- AE fault monitoring during the steady phase of penicillin fermentation process |
|
图 12 青霉素发酵过程稳定阶段DDEFCM-sub-PCA监测结果 Fig.12 DDEFCM-sub-PCA fault monitoring during the steady phase of penicillin fermentation process |
|
|
表 6 3种方法的故障检测率对比 Table 6 Comparison of fault detection rates of three methods |
|
|
表 7 3种方法的故障误警率对比 Table 7 Comparison of fault alarm rate between three methods |
该数据集由北京某生物制药公司采集。根据该公司生产的30批大肠杆菌发酵数据进行离线建模。选取7个相关过程变量如表 8所示。菌体入罐接种后开始采集数据,5 min采样一次,该三维数据集数据特征为Z(30×7×72)。
|
|
表 8 大肠杆菌发酵过程主要过程变量 Table 8 Main variables of recombinant Escherichia coli fermentation process |
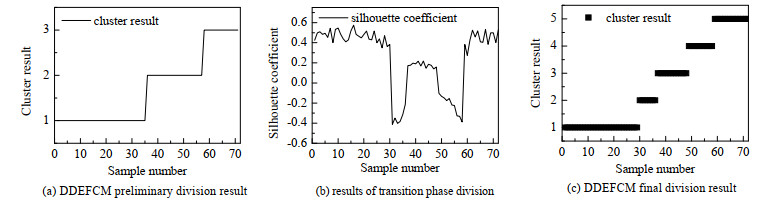
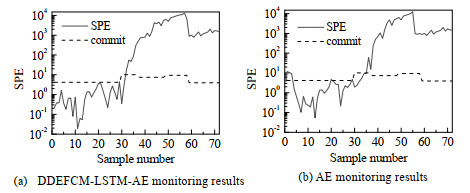
第31个采样时刻设置2% 故障类型的斜坡故障。图 13(a)利用DDEFCM算法对该发酵数据进行初步阶段划分过程。图 13(b)为过渡阶段识别图,可知过渡阶段为30~36、49~58。图 13(c)是最终阶段划分结果。可以看出,阶段划分结果为:稳定阶段1~29、37~48、59~72。过渡阶段30~36、49~58。阶段划分结束后,利用LSTM-AE模型和传统AE模型对每个子阶段进行故障监测。故障监测如图 14(a)和14(b)所示。从图中可以看出,AE的故障监测方法对发酵过程初始时刻开始出现误报警。且在第36个采样时刻SPE才超出控制限。可见,利用AE方法对该大肠杆菌发酵过程进行在线监测,容易发生误报和漏报现象。而LSTM-AE模型在第31时刻及时进行故障报警,不存在误报和漏报现象。因此,本研究所提出的方法在实际间歇工业过程中有效进行阶段划分,提高故障监测性能,对未来处理间歇过程的多阶段特性具有重要意义。
|
图 13 大肠杆菌发酵过程DDEFCM阶段划分结果图 Fig.13 DDEFCM phase division results of Escherichia coli fermentation process |
|
图 14 大肠杆菌发酵过程故障监测结果 Fig.14 Fault monitoring result in Escherichia coli fermentation process |
本研究提出一种基于DDEFCM的多阶段间歇过程故障监测方法,与前人工作相比,所提方法有以下优势:(1)利用信息熵算法计算FCM的聚类个数,解决了主观确定聚类数的问题,提升了聚类划分性能;(2)克服了传统划分算法未考虑数据非线性特征导致聚类灵敏度降低的问题;(3)利用LSTM-AE算法对稳定阶段和过渡阶段构建监测模型,有效处理因子阶段数据分布差异导致的监测精度下降问题,为处理批次等长的多阶段批处理过程的故障监测问题提供了进一步的研究思路。
| [1] |
YAO Y, GAO F. A survey on multiphase statistical modeling methods for batch processes[J]. Annual Reviews in Control, 2009, 33(2): 172-183. DOI:10.1016/j.arcontrol.2009.08.001 |
| [2] |
SIMOGLOU A, GEORGIEVA P, MARTIN E B, et al. On-line monitoring of a sugar crystallization process[J]. Computers & Chemical Engineering, 2005, 29(6): 1411-1422. |
| [3] |
LAWRENCE X Y. Pharmaceutical quality by design: Product and process development, understanding, and control[J]. Pharmaceutical Research, 2008, 25(10): 781-791. |
| [4] |
LU N, GAO F, YANG Y, et al. PCA-based modeling and on-line monitoring strategy for uneven-length batch processes[J]. Industrial & Engineering Chemistry Research, 2004, 43(13): 3343-3352. |
| [5] |
ZHANG S M, ZHAO C H, GAO F R. Incipient fault detection for multiphase batch processes with limited batches[J]. IEEE Transactions on Control Systems Technology, 2017, 27(1): 103-117. |
| [6] |
JIANG Q C, YAN S F, YAN X F, et al. Data-driven two-dimensional deep correlated representation learning for nonlinear batch process monitoring[J]. IEEE Transactions on Industrial Informatics, 2020, 16(4): 2839-2848. DOI:10.1109/TII.2019.2952931 |
| [7] |
RENDALL R, CHIANG L H, REIS M S. Data-driven methods for batch data analysis - A critical overview and mapping on the complexity scale[J]. Computers & Chemical Engineering, 2019, 124: 1-13. |
| [8] |
ZHU J L, GAO F R. Similar batch process monitoring with orthogonal subspace alignment[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 8173-8183. DOI:10.1109/TIE.2018.2803785 |
| [9] |
LUO L K, YAO Y, GAO F R, et al. Mixed-effects Gaussian process modeling approach with application in injection molding processes[J]. Journal of Process Control, 2018, 62: 37-43. DOI:10.1016/j.jprocont.2017.12.003 |
| [10] |
高学金, 孟令军, 王豪, 等. 基于分步时空JITL-MKPLS的间歇过程故障监测[J]. 高校化学工程学报, 2021, 35(1): 127-139. GAO X J, MENG L J, WANG H, et al. Fault monitoring of batch processes based on substep time-space JITL-MKPLS[J]. Journal of Chemical Engineering of Chinese Universities, 2021, 35(1): 127-139. |
| [11] |
WANG R, EDGAR T F, BALDEA M, et al. A geometric method for batch data visualization, process monitoring and fault detection[J]. Journal of Process Control, 2018, 67: 197-205. DOI:10.1016/j.jprocont.2017.05.011 |
| [12] |
JIANG Q C, GAO F R, YAN X F, et al. Multiobjective two-dimensional CCA-based monitoring for successive batch processes with industrial injection molding application[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3825-3834. DOI:10.1109/TIE.2018.2860571 |
| [13] |
高学金, 刘腾飞, 徐子东, 等. 基于循环自动编码器的间歇过程故障监测[J]. 化工学报, 2020, 71(7): 3172-3179. GAO X J, LIU T F, XU Z D, et al. Intermittent process fault monitoring based on recurrent autoencoder[J]. CIESC Journal, 2020, 71(7): 3172-3179. |
| [14] |
LU N, GAO F, WANG F. A sub-PCA modeling and online monitoring strategy for batch processes[J]. AIChE Journal, 2004, 50(1): 255-259. DOI:10.1002/aic.10024 |
| [15] |
BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[J]. Advanced Applications in Pattern Recognition, 1981, 22(1171): 203-239. |
| [16] |
VERMA H, GUPTA A, KUMAR D. A modified intuitionistic fuzzy C-means algorithm incorporating hesitation degree[J]. Pattern Recognition Letters, 2019, 122: 45-52. DOI:10.1016/j.patrec.2019.02.017 |
| [17] |
KHALILIA M A, BEZDEK J, POPESCU M, et al. Improvements to the relational fuzzy C-means clustering algorithm[J]. Pattern Recognition, 2014, 47(12): 3920-3930. |
| [18] |
WU Z, WU Z, ZHANG J. An improved FCM algorithm with adaptive weights based on SA-PSO[J]. Neural Computing and Applications, 2017, 28(12): 3113-3118. |
| [19] |
王骏, 刘欢, 蒋亦樟, 等. 堆叠隐空间模糊C均值聚类算法[J]. 控制与决策, 2016, 31(9): 1671-1677. WANG J, LIU H, JIANG Y Z, et al. Stacked hidden space fuzzy C-means clustering algorithm[J]. Control and Decision, 2016, 31(9): 1671-1677. |
| [20] |
COIFMAN R R, LAFON S. Diffusion maps[J]. Applied and Computational Harmonic Analysis, 2006, 21(1): 5-30. |
| [21] |
LAFON S, LEE A B. Diffusion maps and coarse-graining: A unified framework for dimensionality reduction, graph partitioning, and data set parameterization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(9): 1393-1403. |
| [22] |
KORONAKI E D, NIKAS A M, BOUDOUVIS A G. A data -driven reduced -order model of nonlinear processes based on diffusion maps and artificial neural networks[J]. Chemical Engineering Journal, 2020, 397: 125475. |
| [23] |
TANG X C, LI Y. Phase division and transition modeling based on the dominant phase identification for multiphase batch process quality prediction[J]. Transactions of the Institute of Measurement and Control, 2020, 42(5): 1022-1036. |
| [24] |
MALLAK A, FATHI M. Sensor and component fault detection and diagnosis for hydraulic machinery integrating LSTM autoencoder detector and diagnostic classifiers[J]. Sensors, 2021, 21(2): 433. |
| [25] |
高学金, 刘爽爽, 高慧慧. 基于多变量卷积神经网络的发酵过程故障监测[J]. 高校化学工程学报, 2020, 34(6): 1511-1519. GAO X J, LIU S S, GAO H H. Fault monitoring of fermentation processes based on multivariable convolution neural network[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(6): 1511-1519. |
| [26] |
YAN W W, GUO P J, GONG L, et al. Nonlinear and robust statistical process monitoring based on variant autoencoders[J]. Chemometrics & Intelligent Laboratory Systems, 2016, 158: 31-40. |
| [27] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. |
| [28] |
郭新辰, 郗仙田, 樊秀玲, 等. 基于半监督的模糊C-均值聚类算法[J]. 吉林大学学报(理学版), 2015, 53(4): 705-709. GUO X C, XIAO X T, FAN X L, et al. Fuzzy c-means clustering algorithm based on semi-supervised learning[J]. Journal of Jilin University, 2015, 53(4): 705-709. |
| [29] |
邱天, 丁艳军, 吴占松. 基于主元分析的故障可检测性的统计指标比较[J]. 清华大学学报(自然科学版), 2006(8): 1447-1450. QIU T, DING Y J, WU Z S. Sensor fault detection statistics based on principal component analysis[J]. Journal of Tsinghua University (Science and Technology), 2006(8): 1447-1450. |
| [30] |
王普, 曹彩霞, 高学金, 等. 基于扩展得分矩阵的多阶段间歇过程质量预测[J]. 高校化学工程学报, 2019, 33(3): 664-671. WANG P, CAO C X, GAO X J, et al. Quality prediction of multiphase batch processes based on extended score matrices[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(3): 664-671. |
| [31] |
王普, 李春蕾, 高学金, 等. 基于角结构统计量的MKECA间歇过程故障监测[J]. 仪器仪表学报, 2017, 38(1): 174-180. WANG P, LI C L, GAO X J, et al. Research on batch process monitoring method based on multi-way kernel entropy component analysis and angular structure statistic[J]. Chinese Journal of Scientific Instrument, 2017, 38(1): 174-180. |
| [32] |
BIROL G, UNDEY C, CINAR A. A modular simulation package for fed-batch fermentation: Penicillin production[J]. Computers and Chemical Engineering, 2002, 26(11): 1553-1565. |




