2. 四川大学 水利水电学院, 四川 成都 610065;
3. 湖南科技大学 机电工程学院, 湖南 湘潭 411201
2. College of Water Resource & Hydro Power, Sichuan University, Chengdu 610065, China;
3. School of Mechanical Engineering, Hunan University of Science and Technology, Xiangtan 411201, China
工业生产的许多关键技术都涉及弹状流理论,如化工搅拌器的气液传质、石油和天然气高效混输以及废水处理中的气力提升问题[1-2]。弹状流模型的精确性已成为解决这些技术难题的关键[3-4]。
在弹状流中,气相在运动过程中不断发生脱落与融合。这种边破碎、边融合的复杂水动力学特性给工业装备的设计与控制带来了极大的挑战。国内外研究者提出了大量弹状流理论模型,如Nicklin等[5]与Collins等[6]提出了泰勒气泡漂移速度模型;Brown[7]与Goldsmith等[8]提出了液膜下滑速度与厚度模型;Abraham等[9]研究了液柱长度分布规律并建立了液柱长度模型;Brauner等[10]基于质量守恒方程推导了液相速度方程;Fernandes等[11]与Mao等[12]结合泰勒气泡与液柱流动特性形成了比较完整的弹状流水动力学模型。这些模型在一定程度上为气液两相流装备设计提供了较好的指导作用,但大多是基于泰勒气泡恒定不变假设,没有考虑气泡的破碎与融合效应,造成气泡预测速度过低[13]。就气泡破碎机理而言,现有的研究大多是针对球形或椭球形气泡提出的一种湍流涡破碎机制[14-19],而泰勒气泡破碎是一种黏性剪切与湍流涡碰撞诱发的尾部脱落过程[20-21]。就气泡融合而言,现有模型大多是基于气泡随机碰撞提出的概率融合模型[22],而弹状流中泰勒气泡与小气泡融合实际上是一种定向追赶融合。一旦上游小气泡速度低于下游泰勒气泡时,泰勒气泡与小气泡融合,即发生追赶融合。
为了建立精准的弹状流模型,本研究考虑黏性剪切与湍流涡碰撞,建立泰勒气泡的破碎模型。基于气相质量守恒法,推导了弹状流的气泡融合模型。结合破碎模型、融合模型以及经典的弹状流理论,形成了更为精准的弹状流理论模型。研究结果丰富了气液两相流理论,可为复杂流体装备的设计和控制提供理论支撑。
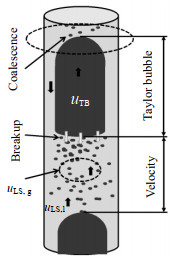
2 理论建模大量研究者[10-13]对弹状流结构进行分析,将弹状流流动单元划分为如图 1所示的泰勒气泡段和液柱段。在泰勒气泡段,泰勒气泡呈子弹状,以速度uTB向上运动,液膜沿其周围做下滑运动,下滑速度为uLf。在液柱段,液体呈连续相状,以速度uLS, l向上运动,小气泡呈球状或椭球状,粒径为0~3.2 mm,均匀分布在连续液体中,以速度uLS, g向上运动[23]。在泰勒气泡段与液柱段的交界处,泰勒气泡尾部不断脱落,形成大量小气泡群。这种小气泡群游离于液柱中,一旦速度低于下游泰勒气泡时,能与下游泰勒气泡重新融合。
|
图 1 弹状流模型 Fig.1 Slug flow model |
下滑液膜不断与上升泰勒气泡发生剪切,并与下游液柱发生碰撞,在交界区域形成强湍流场。一旦该湍流场的湍动能大于泰勒气泡的表面张力能,气泡尾部发生破碎。对泰勒气泡尾部湍动场分析可知,该区域的湍动能与气液剪切速度和湍动脉动量相关[10],可表示为
| $ E = \frac{1}{2}{\rho_{\rm{l}}}({u_x}^2 + {u_y}^2 + {u_z}^2){u_{{\rm{Lf, TB}}}}$ | (1) |
式中:E为湍动能,W;uLf, TB为液膜与泰勒气泡的剪切速度,m⋅s−1;ux,uy,uz为湍动区域剪切层的空间三维方向脉动速度,m⋅s−1;ρl为液体密度,kg⋅m−3。
液膜与泰勒气泡的剪切速度可表示为[10]
| $ {u_{{\rm{Lf, TB}}}}{\text{ = }}({u_{\rm{TB}}} - {u_{{\rm{Lf}}}})(1 - {\varepsilon _{{\text{TB}}}}) $ | (2) |
式中:uTB为泰勒气泡速度,m⋅s−1;uLf为液膜速度,m⋅s−1;εTB为泰勒气泡段含气率。
湍流场的脉动量是由下滑液膜与上升液柱的迎面碰撞引起,Brauner等[10]对该处湍流脉动量进行了测量,提出湍流脉动量的经验表达式:
| $ {u_x}^2 + {u_y}^2 + {u_z}^2 = 0.03{({u_{{\rm{LS, l}}}} - {u_{{\rm{Lf}}}})^2} $ | (3) |
式中:uLS, l为液柱中液体的速度,m⋅s−1。
泰勒气泡由于表面张力作用,具有一定的变形抵抗能力。气泡表面张力能可表示为[10]
| $ {E_ {\rm{c}}} = \frac{\sigma }{{{d_{\max }}}}{u_{{\rm{Lf, TB}}}} $ | (4) |
式中:Ec为泰勒气泡表面张力能,W;
| $ {d_{\max }} = 0.{\text{634}}\sqrt {\frac{\sigma }{{({\rho _{\text{l}}} - {\rho _{\text{g}}})g}}} $ | (5) |
式中:ρg为气体密度,kg ⋅m−3;g为重力加速度,m⋅s−2。
根据能量守恒定理,泰勒气泡的有效破碎能可表示为湍动能与表面张力能之差,即:
| $ {E_ {\rm{s}}} = E - {E_ {\rm{c}}} $ | (6) |
式中:Es为气泡有效破碎能, W。
这种有效破碎能致使泰勒气泡尾部发生脱落,脱落速度与有效破碎能呈正比[10],可表示为
| $ {u_ {\rm{TB, g1}}} = \frac{{{d_{{\rm{max}}}}}}{{6\sigma }}{E_ {\rm{s}}} $ | (7) |
式中:uTB, g1为泰勒气泡尾部脱落速度,m⋅s−1。
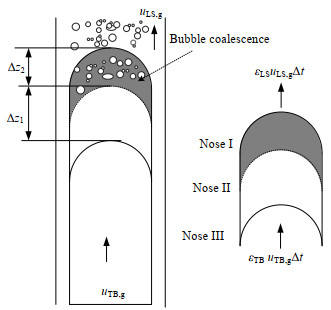
2.2 泰勒气泡鼻部融合机理液柱中小气泡能与下游泰勒气泡发生融合,这种融合效应改变了泰勒气泡鼻尖位置,增大了泰勒气泡的有效移动速度。假设不考虑融合过程中泰勒气泡鼻尖的变形,其融合机理可简化为如图 2所示过程。在时间间隔Δt内,不考虑融合效应,泰勒气泡鼻尖由位置Ⅰ运动到位置Ⅱ。但由于气泡融合效应,泰勒气泡的鼻尖位置将向上移,假设其融合后泰勒气泡鼻尖移动到位置Ⅲ。取位置Ⅰ、位置Ⅲ、管壁围成的区域为控制体积。在初始时刻t = 0,泰勒气泡尚未进入该控制体积。此时,该控制体积内气体的体积为
| $ {V_0} = (\Delta {z_1} + \Delta {z_2})A{\varepsilon _{{\text{LS}}}} $ | (8) |
|
图 2 泰勒气泡鼻部融合 Fig.2 Taylor bubble coalescence in a control volume |
式中:V0为控制体在t=0时气相体积,m3;Δz1为泰勒气泡移动距离,m;Δz2为泰勒气泡鼻部融合长度,m;A为管道横截面积,m2;εLS为液柱段含气率。
在t=Δt(Δt为时间间隔,s)时刻,泰勒气泡完全占据该控制体积,控制体积内气体的体积为
| $ {V_{\Delta t}} = (\Delta {z_1} + \Delta {z_2})A{\varepsilon _{{\text{TB}}}} $ | (9) |
式中:VΔt为控制体初始气相体积,m3。
对控制体积而言,其流入的气体体积为
| $ {V_{{\text{in}}}} = {\varepsilon _{{\text{TB}}}}{u_{{\text{TB, g}}}}A\Delta t $ | (10) |
式中:uTB, g为泰勒气泡中气相运动速度,m⋅s−1;Vin为流入控制体的气体体积,m3。
流出控制体的气体体积为
| $ {V_{{\text{out}}}} = {\varepsilon _{{\text{LS}}}}{u_{{\text{LS, g}}}}A\Delta t $ | (11) |
式中:uLS, g为液柱中气相上升速度,m⋅s−1;Vout为流出控制体的气体体积,m3。
因此,根据气相质量守恒可得
| $ {V_{\Delta t}} - {V_0} = {V_{{\text{in}}}} + {V_{{\text{out}}}} $ | (12) |
将式(8)~(11)代入(12)可得
| $ \frac{{\Delta {z_1} + \Delta {z_2}}}{{\Delta t}} = {u_{{\text{TB, g}}}} + \frac{{{\varepsilon _{{\text{LS}}}}\left( {{u_{{\text{TB, g}}}} - {u_{{\text{LS, g}}}}} \right)}}{{{\varepsilon _{{\text{TB}}}}}} $ | (13) |
泰勒气泡的真实速度为
| $ {u_{{\rm{TB}}}} = \frac{{\Delta {z_1} + \Delta {z_2}}}{{\Delta t}} $ | (14) |
因此,由式(13)~(14)可得,泰勒气泡的真实速度为
| $ {u_{{\rm{TB}}}} = {u_{{\text{TB, g}}}} + \frac{{{\varepsilon _{{\text{LS}}}}\left( {{u_{{\text{TB, g}}}} - {u_{{\text{LS, g}}}}} \right)}}{{{\varepsilon _{{\text{TB}}}}}} $ | (15) |
泰勒气泡的真实速度是气相运动速度与气泡融合速度之和。从式(15)可得,气泡融合速度为
| $ \Delta {u_{\text{c}}} = \frac{{{\varepsilon _{{\text{LS}}}}\left( {{u_{{\text{TB, g}}}} - {u_{{\text{LS, g}}}}} \right)}}{{{\varepsilon _{{\text{TB}}}}}} $ | (16) |
式中:
对于稳定流动弹状流,泰勒气泡的总长度保持不变,因此脱落速度与融合速度满足:
| $ {u_{\rm{TB, g1}}}{\text{ = }}{\varepsilon _{{\text{LS}}}}\Delta {u_{\text{c}}} $ | (17) |
对于泰勒气泡的运动,Fernandes等[11]与Mao等[21]认为泰勒气泡中气相速度可以等效为混合流体速度与泰勒气泡漂移速度的组合叠加:
| $ {u_{{\rm{TB, g}}}} = C_{{\text{TB}}, 0}^{}{u_{\rm{m}}} + u_{{\text{TB}}, {\text{0}}}^{} $ | (18) |
式中:
静水中泰勒气泡的漂移速度与液体密度及管道直径有关,目前针对静水中泰勒气泡漂移速度,较为常用的模型是Zukoski模型[10]。
| $ u_{{\text{TB}}, {\text{0}}}^{} = 0.35{(\frac{{{\rho _{\text{l}}} - {\rho _{\text{g}}}}}{{{\rho _l}}}gD)^{1/2}} $ | (19) |
式中:D为管道直径,m。
液膜围绕泰勒气泡做下滑运动,
| $ {u_{{\text{Lf}}}} = \frac{{{u_ {\rm{m}}} - {\varepsilon _{{\text{TB}}}}{u_{{\text{TB, g}}}}}}{{1 - {\varepsilon _{{\text{TB}}}}}} $ | (20) |
液柱中气液两相的运动规律符合经典的漂移模型。对于气泡群,其速度表达式与混合流体的速度有关,如式(21)所示:
| $ {u_{{\text{LS, g}}}} = {C_0}{u_ {\rm{m}}} + {u_0} $ | (21) |
式中:C0为气泡群分布参数,u0为气泡在流体的漂移速度,m⋅s−1。
根据混合流体速度的计算方法,可求出液柱中液体的速度:
| $ {u_{{\text{LS, l}}}} = \frac{{{u_ {\rm{m}}} - {\varepsilon _{{\text{LS}}}}{u_{{\text{LS, g}}}}}}{{1 - {\varepsilon _{{\text{LS}}}}}} $ | (22) |
对于气泡群在液体中的漂移速度,Brauner等[10]认为该速度与气液密度及含气率大小有关,提出了式(23)所示的经验公式。
| $ {u_{\text{0}}}{\text{ = }}1.53{\left[ {\frac{{\sigma g({\rho _{\text{l}}} - {\rho _{\text{g}}})}}{{\rho _{\text{l}}^{\text{2}}}}} \right]^{0.25}}{(1 - {\varepsilon _{{\text{LS}}}})^{1.5}} $ | (23) |
张井志等[24]、汪志能等[25]研究了层流和湍流工况下泰勒气泡段含气率,认为临界雷诺数为750时,弹状流液膜由层流向湍流运动转变。基于此,Cachard等[26]提出了泰勒气泡段含气率模型,
| $ {\varepsilon _{{\text{TB}}}} = \left\{ \begin{gathered} {(1 - {( - 3{u_{{\text{Lf}}}}(\frac{{{v_{\text{L}}}}}{{g{D^2}}}))^{0.5}})^2}{{\qquad}}R{e_ {\rm{F}}} < 750 \hfill \\ {(1 - \frac{{u_{{\text{Lf}}}^{\text{2}}}}{{{\text{125}}{\text{.44}}gD}})^2}{{\qquad\qquad\qquad}}R{e_ {\rm{F}}} \geqslant 750 \hfill \\ \end{gathered} \right. $ | (24) |
式中:νL为液体运动黏度,m2⋅s−1;
经典的弹状流模型一般采用计算流体动力学(CFD)计算,但CFD软件一般不考虑泰勒气泡的形变影响,难以描述气泡运动与破碎、融合的耦合规律。为此提出一种自主编程计算方法。对模型(1)~(24)进行分析,该模型是一个极为复杂的非线性方程组,涉及大量未知流动参数。对新建模型进行数学分析,模型可化简成式(25)~(32):
| $ {u_{{\text{TB, g}}}}{\text{ = }}C_{{\rm{TB, 0}}}^{}{u_ {\rm{m}}} + 0.35{(\frac{{{\rho _ {\rm{l}}} - {\rho _{\text{g}}}}}{{{\rho _{\text{l}}}}}gD)^{1/2}} $ | (25) |
| $ {u_{{\text{Lf}}}} = \frac{{{u_ {\rm{m}}} - C_{ {\rm{TB, 0}}}^{}{u_ {\rm{m}}}{\varepsilon _{{\text{TB}}}} - 0.35{\varepsilon _{{\text{TB}}}}{{(\frac{{{\rho _ {\rm{l}}} - {\rho _{\text{g}}}}}{{{\rho _{\text{l}}}}}gD)}^{1/2}}}}{{1 - {\varepsilon _{{\text{TB}}}}}} $ | (26) |
| $ {u_{{\text{LS, g}}}} = {C_0}{u_ {\rm{m}}} + 1.53{\left[ {\frac{{\sigma g({\rho _ {\rm{l}}} - {\rho _{\text{g}}})}}{{\rho _{\text{l}}^{\text{2}}{{(1 - {\varepsilon _{{\text{LS}}}})}^{ - 6}}}}} \right]^{0.25}} $ | (27) |
| $ {u_{{\text{LS, l}}}}{\text{ = }}\frac{{(1 - {\varepsilon _{{\text{LS}}}}{C_0})}}{{1 - {\varepsilon _{{\text{LS}}}}}}{u_ {\rm{m}}} - 1.53{\left[ {\frac{{\sigma g({\rho _{\text{l}}} - {\rho _{\text{g}}}){{(1 - {\varepsilon _{{\text{LS}}}})}^2}}}{{\rho _{\text{l}}^{\text{2}}\varepsilon _{{\text{LS}}}^{{\text{ - 4}}}}}} \right]^{0.25}} $ | (28) |
| $ \begin{array}{l} {u}_{{\rm{TB, g1}}}{\text{ = }}\frac{{0.{\text{634}}}}{{400D}}\frac{{{\sigma ^{0.5}}}}{{{{({\rho _{\text{l}}} - {\rho _g})}^{0.5}}{{\rm{g}}^{0.5}}}}\{ \frac{{{\rho _{\text{l}}}D}}{\sigma }{\text{[}}\frac{{1 - {\varepsilon _{{\text{LS}}}}{C_0}}}{{1 - {\varepsilon _{{\text{LS}}}}}}{u_ {\rm{m}}} - 1.53{\varepsilon _{{\text{LS}}}}\frac{{{\sigma ^{0.25}}{g^{0.25}}{{({\rho _{\text{l}}} - {\rho _{\text{g}}})}^{0.25}}}}{{\rho _ {\rm{l}}^{{\text{0}}{\text{.5}}}}}{(1 - {\varepsilon _{{\text{LS}}}})^{0.5}} - \hfill \\ {\begin{array}{*{20}{c}} {}&{} \qquad \end{array}_{}}_{}\frac{{1 - {\varepsilon _{{\text{TB}}}}C_{{\text{TB}}, 0}^{}}}{{1 - {\varepsilon _{{\text{TB}}}}}}{u_ {\rm{m}}} + \frac{{0.35{\varepsilon _{{\text{TB}}}}}}{{1 - {\varepsilon _{{\text{TB}}}}}}{(\frac{{{\rho _{\text{l}}} - {\rho _{\text{g}}}}}{{{\rho _{\text{l}}}}}gD)^{0.5}}{]^2} - 105.1D\frac{{{{({\rho _{\text{l}}} - {\rho _{\text{g}}})}^{0.5}}{g^{0.5}}}}{{{\sigma ^{0.5}}}}\} {\text{\{ }}{u_{{\rm{TB}}}} - \frac{{{u_ {\rm{m}}}}}{{1 - {\varepsilon _{{\text{TB}}}}}} + \hfill \\ {\begin{array}{*{20}{c}} {}&{} \qquad\end{array}_{}}_{}\frac{{{\varepsilon _{{\text{TB}}}}}}{{1 - {\varepsilon _{{\text{TB}}}}}}[C_{{\text{TB}}, 0}^{}{u_ {\rm{m}}} + 0.35{(\frac{{{\rho _{\text{l}}} - {\rho _{\text{g}}}_{}}}{{{\rho _{\text{l}}}}}gD)^{1/2}}]{\text{\} }}(1 - {\varepsilon _{{\text{TB}}}}) \hfill \\ \end{array} $ | (29) |
| $ {u_{{\rm{TB}}}} = \frac{{{u_{{\text{TB, g}}}}{\varepsilon _{{\text{TB}}}} - {u_{{\text{LS, g}}}}{\varepsilon _{{\text{LS}}}}}}{{{\varepsilon _{{\text{TB}}}} - {\varepsilon _{{\text{LS}}}}}} $ | (30) |
| $ {\varepsilon _{{\text{LS}}}} = \sqrt {\frac{{{u_ {\rm{TB, g1}}}{\varepsilon _{{\text{TB}}}}}}{{{u_{{\text{TB}}}} - {u_{{\text{LS, g}}}}}}} $ | (31) |
| $ {\varepsilon _{TB}} = \left\{ \begin{gathered} {(1 - {( - 3{u_{{\text{Lf}}}}(\frac{{{v_{\text{L}}}}}{{g{D^2}}}))^{0.5}})^2}{{\qquad}}R{e_{{\rm{Lf}}}} < 750 \hfill \\ {(1 - \frac{{u_{{\text{Lf}}}^{\text{2}}}}{{{\text{125}}{\text{.44}}gD}})^2}{{\qquad\qquad}}R{e_{{\rm{Lf}}}} \geqslant 750 \hfill \\ \end{gathered} \right. $ | (32) |
在给定的流动工况下,方程式(25)~(29)是3个变量(uT、εTB、εLS)的显式方程,方程(30)~(32)是3个变量(uTB、εTB、εLS)的隐式方程。因此,以式(30)~(32)为主方程,以式(25)~(29)为辅助方程,采用最小二乘迭代法求解uTB、εTB、εLS,计算参数如表 1所示。设置已知参数(如:um、D、νL、σ),给定uTB、εTB、εLS初值,计算显式方程(23)~(25),获得弹状流的气相速度和液相速度(uTB, g、uLf、uLS, l、uLS, g),以及泰勒气泡尾部脱落速度uTB, g1,将计算结果(uTB, g、uLf、uLS, l、uLS, g、uTB, g1)代入方程组(30)~(32)左边,重新计算获取uTB、εTB、εLS,对比uT、εTB、εLS的计算结果与其初始值,如果误差超过3%,则选择合适的步长,更新uTB、εTB、εLS初值,重新进行计算,直至误差小于3%,获得最终的uTB、εTB、εLS。将最终uTB、εTB、εLS代入方程(25)~(29),获得uTB, g、uLf、uLS, l、uLS, g、uTB, g1。
|
|
表 1 数值计算参数 Table 1 Parameter values for calculation |
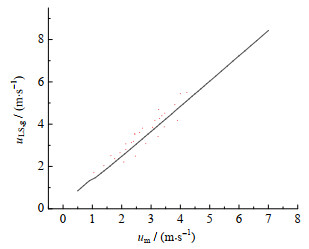
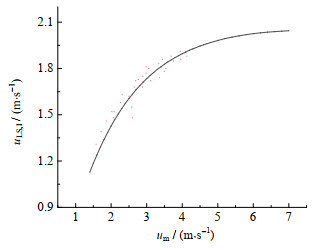
对弹状流水动力学特性进行计算分析,结果如图 3~6所示。图 3~6中,管道直径为30 mm,混合流体速度范围为0.5~7 m⋅s−1。小气泡在液体中做漂移运动,其速度随混合流体速度的变化曲线如图 3所示。小气泡速度与混合流体速度正相关。液柱中液体速度随混合流体速度变化规律如图 4所示,随着混合流体速度的增加,液体流速的增长量逐渐放缓,最后趋于平稳。与小气泡速度相比,液相速度变化规律较为复杂。液柱中的液流是一种受迫运动,即液体夹在两泰勒气泡之间,受上游气泡卷吸和下游气泡推动双重作用。在混合流体速度不高的工况下(um < 4 m⋅s−1),液柱长度较短,液体震动式升沉运动并不明显,液流速度随混合流体速度增长而增长;在混合流体速度较高的工况下(um > 4 m⋅s−1),液柱长度变长,液流的震动式升沉运动越明显,泰勒气泡的推动与卷吸能力有限,液流的加速效应逐渐放缓。
|
图 3 小气泡速度随混合流体速度变化曲线 Fig.3 Bubble velocity versus fluid mixture velocity |
|
图 4 液柱中液体速度随混合流体速度变化曲线 Fig.4 Liquid velocity versus fluid mixture velocity |
|
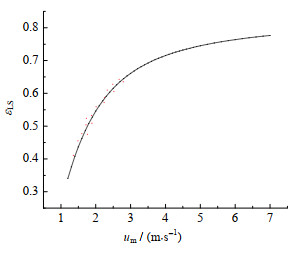
图 5 液柱含气率随混合流体速度变化曲线 Fig.5 Void fraction in slug versus fluid mixture velocity |
|
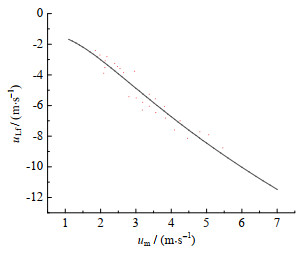
图 6 液膜速度随混合流体速度变化曲线 Fig.6 Liquid film velocity versus fluid |
液柱的含气率随混合流体速度变化曲线如图 5所示,随着混合流体速度增加,含气率先迅速增加后逐步趋于平稳。随着混合流体速度的增加,液柱中气泡平均直径变小,气泡变密集,含气率随之增大。当气泡过于密集时,易融合成气团,并最终融入下游泰勒气泡。因此,当混合流体速度较高时,液柱中含气率的增长速度逐渐变慢。
液膜速度随混合流体速度的变化规律如图 6所示,与泰勒气泡速度方向相反,液膜沿着管壁做下滑运动。随混合流体速度增加,液膜下滑速度越大,且下滑速度高于混合流体速度。泰勒气泡凸形鼻部对周围液流挤压,导致液体流向管壁附近,形成下滑液膜。液膜受自身重力、管壁摩擦以及气液界面剪切应力的影响,其稳定下滑速度与液膜厚度有关。混合流体速度越大,液膜越厚,维持液膜平衡的管壁摩擦力与气液剪切力也越大,故液膜的下滑速度也越大。
泰勒气泡脱落量随混合流体速度的变化关系如图 7所示。在低流速工况下(um < 1.2 m⋅s−1),泰勒气泡尾部湍流强度不大,泰勒气泡未发生破碎。当混合流体速度超过1.2 m⋅s−1时,泰勒气泡开始发生破碎,且气泡破碎量随混合流体速度增加逐渐增加。混合流体速度增大,液膜长度、下滑速度以及液柱上升速度均增大,液膜与液柱撞击越剧烈,泰勒气泡尾流区域更易发生破碎。

|
图 7 气泡脱落速度随混合流体变化曲线 Fig.7 Bubble breakup velocity versus fluid mixture velocity |
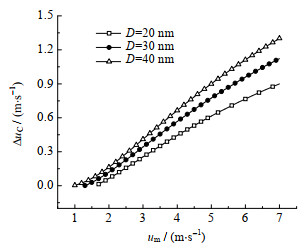
气泡融合速度随混合流体速度的变化关系如图 8所示。当um < 1.5 m⋅s−1时,气泡融合增长速度相对较缓。在低速工况下,气相的速度较低,泰勒气泡与小气泡的追赶融合概率较低。低速工况下气泡间排液较慢,气泡融合所需时间较长。在um > 1.5 m⋅s−1时,混合流体速度增大,增加了液柱下游小气泡碰撞概率,大量小气泡直接融合成小气团,然后与下游泰勒气泡进行二次融合。
|
图 8 气泡融合速度随混合流体变化曲线 Fig.8 Bubble coalescence velocity versus fluid mixture velocity |
管道直径对气泡的破碎和融合具有较大的影响。管道直径越大,泰勒气泡尾部脱落量越大。管道直径一方面能抑制气泡表面张力,削弱气泡抵抗变形的能力。另一方面,管道直径越大,液膜越厚,与液柱对冲作用越强,气泡更易发生破碎。从图 8中还可以发现,管道直径越大,泰勒气泡鼻部的融合速度增大。一方面,管道直径有利于促进小气泡与泰勒气泡的追赶融合。由式(19)与(23)可见,管道直径能增大泰勒气泡的漂移速度,而对小气泡的漂移速度无影响,因此,管道直径增大,泰勒气泡能更快追赶上上游小气泡,并与之发生融合;另外一方面,管道直径增大,导致小气泡产生较大的径向速度,气泡摆动上升过程中,易发生左右剪切碰撞,增大了气泡的融合概率。
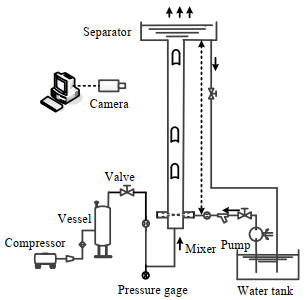
4 实验研究弹状流实验装置如图 9所示,实验在室温环境中进行,工质为空气和水。气液经过混合器混合后,沿着竖直管道向上运动,经过分离器,气体直接排向大气,液体经过分离器循环流向水箱。竖直管道内径40 mm,长度4 000 mm,材质为透明有机玻璃。根据Baker流型图[27],气流表观速度为1.7 ~5.2 m⋅s−1,液流表观速度为0.4~1.2 m⋅s−1。实验过程中,入口液流采用液体流量计(型号:MAG25,精度0.5%)进行测量,入口气流采用气体流量计(型号:LUGB-2403,精度0.5%)进行测量。
|
图 9 实验装置 Fig.9 Experimental setup |
在观测段,加装有机玻璃光学校正箱并对玻璃箱充满与实验介质相同的水液,从而减弱玻璃圆管的光学折射失真。通过激光平面和高速相机捕获此段的弹状流流动图像。激光片光面穿过管道轴心线,高速摄影相机正对片光平面,捕捉该片光平面上气液的流动图像。相机型号:PhantomM310,相机拍摄频率为1 000 Hz。连续激光源为中科院长春新产业光电技术有限公司研发的半导体泵浦全固态激光器,激光器型号:MLL-U-457,输出波长为457 nm,功率为1~400 mW。具体实验流程:(1) 检查管路气密性,开启离心泵给竖直有机玻璃管充液。(2) 开启空压机,调节气体节流阀的开度控制进气量,调节离心泵变频器频率控制进口水流量。(3)管内气液流量相对稳定时记录流量和压力数据。同时采用高速相机拍摄管内的流型变化。
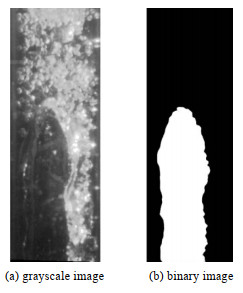
针对弹状流流动图像,Mohmmed等[27]提出了Matlab图形处理方法:对原始图像进行预处理,将彩色图像转为灰度图,并根据气液灰度值的差异,对图像进行增强处理,凸显出气泡的轮廓,如图 10(a)所示。采用轮廓检测技术识别泰勒气泡边界,利用图像填充、腐蚀以及Blob区域提取方法,获取泰勒气泡的二值化图像,如图 10(b)所示。Matlab流程图见文献[27]。根据泰勒气泡二值化图像,Mohmmed等[27]提出了泰勒气泡上升速度的计算方法:每隔N帧选取两图像,记录两图像中泰勒气泡的鼻尖位置(z1、z2),通过两图像中泰勒气泡的上升距离与时间计算其上升速度:
| $ {u_{{\rm{TB}}}}{\text{ = }}\frac{{{z_1} - {z_2}}}{{N/{f_ {\rm{s}}}}} $ | (33) |
|
图 10 弹状流图像处理结果 Fig.10 Image processing of slug flow |
式中:z1、z2为两图片中泰勒气泡鼻尖的高度,m;N为帧数;fs为相机频率,Hz。
对泰勒气泡上升速度误差进行分析,考虑到测量和高速摄影的不确定性。根据Moffa误差理论[28],泰勒气泡速度误差来源包括测量误差和气液图像的分辨率,
| $ {e_ {\rm{r}}} = \sqrt {e_ {\rm{a}}^2 + e_ {\rm{b}}^2} $ | (34) |
式中:er为总误差,ea为测量误差,eb为图像的像素误差。
对泰勒气泡图像进行分析,图像分辨率为2 048×1 952,对应两相邻像素点的实际距离为0.03 mm,即泰勒气泡图像的最大偏差为0.03 mm。根据式(33)中泰勒气泡速度计算方法,可得在帧数为100的情况下,由于图像分辨率引起的最大误差为3×10−5 m⋅s−1。对泰勒气泡速度进行多次重复测量,测量误差可通过Moffa误差理论[28]获得
| $ {e_ {\rm{a}}} = 1.24\sqrt {\frac{{\sum\limits_{i = 1}^k {{{({u_{{\rm{TB}}, i}} - {u_{{\rm{TB, av}}}})}^2}} }}{{k - 1}}} $ | (35) |
式中:k为测量次数;uTB, i为泰勒气泡第i次测量的速度,m⋅s−1;uTB, av为泰勒气泡平均测量速度,m⋅s−1。
根据图像分辨率与测量误差计算式(35),可求得在10次重复测量下,泰勒气泡速度的相对误差控制在1%以内,符合测量要求。
泰勒气泡尾部往往具有气泡连续脱落的特点。如图 11所示,该工况的气相表观速度usup, g=3.2 m⋅s−1,液相表观速度usup, l=1.1 m⋅s−1。泰勒气泡尾部不再平坦,在中部形成尖形凹陷,并伴有大量气泡脱落。在泰勒气泡尾部湍动区域中:下滑液膜剪切泰勒气泡,致使泰勒气泡尾部形成了凹陷界面,大量气泡从凹陷界面脱落。这种凹陷界面不稳定,并迅速向两边扩展,最终形成较为平坦的破碎界面。

|
图 11 气泡破碎图像 Fig.11 Bubble breakage |
对于低进气量工况,液柱段含气率较低,小气泡较为稀疏,相互碰撞不明显。在该工况下,液柱中小气泡的速度低于下游泰勒气泡,小气泡与泰勒气泡形成了追赶融合。对于中等或高进气量工况,液柱中小气泡密集性较高,如图 12所示。该工况的气相表观速度usup, g=3.2 m⋅s−1,液相表观速度usup, l=1.1 m⋅s−1。在轴向位置上,小气泡群在下游发生了聚合,形成了局部气团,并与下游泰勒气泡发生二次融合。

|
图 12 气泡融合图像 Fig.12 Bubble coalescence |
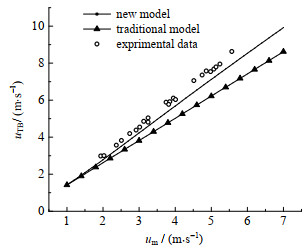
在不同气液速度下进行实验,采用第3节图形处理方法计算泰勒气泡上升速度uTB。根据气液表观速度计算混合流体速度um,绘制um-uTB曲线。D=40 mm,结合实验参数,分别计算出新建模型与传统模型的泰勒气泡上升速度,如图 13所示。由图可见,传统的模型中泰勒气泡在混合流体中做线性漂移,其上升速度与混合流体速度正相关。考虑到气泡融合效应,新建理论模型的泰勒气泡上升速度仍与混合流体速度正相关。这说明气泡融合速度与混合流体速度呈正比,即混合流体速度越快,气泡融合量越大,这与实验结果较为吻合。通过高速摄像实验可以发现气相速度越大,泰勒气泡的追赶融合能力越强;而液流速度越大,小气泡的湍动碰撞效应也越强。
|
图 13 新建模型与传统模型、实验数据对比 Fig.13 Comparison of model result with traditional model and experimental data |
从图 13还可以发现,传统模型忽略气泡的融合效应,其预测速度低于新建理论模型的计算值。新建模型的um-uTB曲线同样呈现线性关系,这说明融合效应增强了泰勒气泡的分布系数
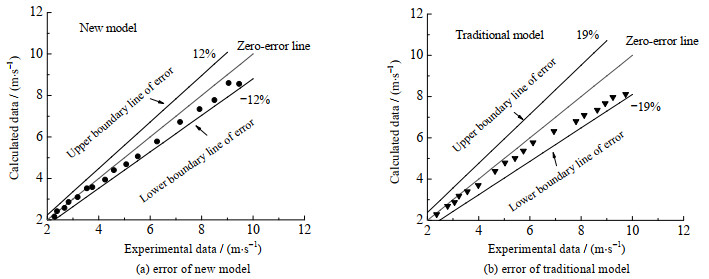
|
图 14 模型误差 Fig.14 Model errors |
与实验结果相比,新建模型的计算速度低于实验速度。随混合流体速度增大,新建模型的计算值明显低于实验速度。从高速摄像图像(图 12)可以发现,在高流速工况下,液柱中小气泡在液柱中能进行第一次局部融合,这种局部融合形成的气团能与下游泰勒气泡发生二次融合。2.2节所建立的融合模型仅考虑一次融合效应的影响,融合速度较慢,造成泰勒气泡的运动速度偏慢,在今后研究中还需加强对气泡二次融合效应的研究。从以上论述可看出,新建模型的计算速度与实验速度虽存在一定差异,但其变化大致趋势与仿真结果基本一致,且误差控制在12%内,较传统模型有较大的提高,这进一步说明本研究构建理论模型合理。
5 结论(1) 建立了基于气泡破碎和融合效应的弹状流理论模型。传统弹状流模型未考虑气泡的融合与脱落特性,与现实工况存在一定的差异。为此,基于湍动能、表面张力能和破碎能能量守恒,推导了泰勒气泡破碎量模型。基于气相质量守恒原理,推导了泰勒气泡速度融合模型。结合气泡破碎模型、速度融合模型以及经典弹状流经验公式,形成了一种更为精确的弹状流理论模型。
(2) 提出一种新型弹状流模型的最小二乘迭代计算方法。有限元计算方法不考虑泰勒气泡的形变特征,难以描述气泡的破碎、融合与运动的耦合规律。为此,以隐式方程为主方程,以显示方程为辅助方程,采用最小二乘迭代法计算,获取弹状流的速度与含气率。
(3) 新建理论模型具有较高的预测精度,能为弹状流装置设计提供可靠的理论指导。与实验数据对比,新建模型误差为12%,较经典理论模型提高了7%。证明考虑气泡融合与破碎效应的理论模型更为合理。
| [1] |
MA H Y, ZHAO Q K, YAO C Q, et al. Effect of fluid viscosities on the liquid-liquid slug flow and pressure drop in a rectangular microreactor[J]. Chemical Engineering Science, 2021, 241: 116697. DOI:10.1016/j.ces.2021.116697 |
| [2] |
HUANG J C, GUO Z W, TANG X Y, et al. A method for void fraction measurement of bubble/slug flow in small channels based on contactless impedance detection[J]. Review of Scientific Instruments, 2021, 92(10): 105006. DOI:10.1063/5.0029772 |
| [3] |
XUE T, ZHAO J Y, WANG Q, et al. Measurement of three-dimensional characteristics of slug flow[J]. IEEE Sensors Journal, 2021, 21(7): 9072-9080. DOI:10.1109/JSEN.2021.3053059 |
| [4] |
LIU A T, CHENG L H, YAN C Q, et al. Experimental study on length, liquid film thickness and pressure drop of slug flow in horizontal narrow rectangular channel[J]. Chemical Engineering Research and Design, 2022, 182: 502-516. DOI:10.1016/j.cherd.2022.04.010 |
| [5] |
NICKLIN D J, WILKES J O, DAVIDSON J F. Two phase flow in vertical tubes[J]. Transactions of the Institution of Chemical Engineers, 1962, 40: 61-68. |
| [6] |
COLLINS R, DE MORAES F F, DAVIDSON J F, et al. The motion of a large gas bubble rising through liquid flowing in a tube[J]. Journal of Fluid Mechanics, 1978, 89: 497-514. DOI:10.1017/S0022112078002700 |
| [7] |
BROWN R A S. The mechanics of large gas bubbles in tubes: Ⅰ. Bubble velocities in stagnant liquids[J]. The Canadian Journal of Chemical Engineering, 1965, 43(5): 217-223. DOI:10.1002/cjce.5450430501 |
| [8] |
GOLDSMITH H L, MASON S G. The movement of single large bubbles in closed vertical tubes[J]. Journal of Fluid Mechanics, 1962, 14(1): 42-58. DOI:10.1017/S0022112062001068 |
| [9] |
DUKLER A E, MARON D M, BRAUNER N. A physical model for predicting the minimum stable slug length[J]. Chemical Engineering Science, 1985, 40(8): 1379-1385. DOI:10.1016/0009-2509(85)80077-4 |
| [10] |
BRAUNER N, ULLMANN A. Modelling of gas entrainment from Taylor bubbles. Part A: Slug flow[J]. International Journal of Multiphase Flow, 2004, 30(3): 239-272. DOI:10.1016/j.ijmultiphaseflow.2003.11.007 |
| [11] |
FERNANDES R C, SEMIAT R, DUKLER A E. Hydrodynamic model for gas-liquid slug flow in vertical tubes[J]. AIChE Journal, 1983, 29(6): 981-989. DOI:10.1002/aic.690290617 |
| [12] |
MAO Z S, DUKLER A E. The motion of Taylor bubbles in vertical tubes-Ⅱ. Experimental data and simulations for laminar and turbulent flow[J]. Chemical Engineering Science, 1991, 46(8): 2055-2064. DOI:10.1016/0009-2509(91)80164-T |
| [13] |
KOCKX J P, NIEUWSTADT F T M, OLIEMANS R, et al. Gas entrainment by a liquid film falling around a stationary Taylor bubble in a vertical tube[J]. International Journal of Multiphase Flow, 2005, 31(1): 1-24. DOI:10.1016/j.ijmultiphaseflow.2004.08.005 |
| [14] |
ZHANG H H, YANG G Y, SAYYAR A, et al. An improved bubble breakup model in turbulent flow[J]. Chemical Engineering Journal, 2020, 386: 121484. DOI:10.1016/j.cej.2019.04.064 |
| [15] |
SHI W B, YANG J, LI G, et al. Modelling of breakage rate and bubble size distribution in bubble columns accounting for bubble shape variations[J]. Chemical Engineering Science, 2018, 187: 391-405. DOI:10.1016/j.ces.2018.05.013 |
| [16] |
施炜斌, 龙姗姗, 杨晓钢, 等. 计及气泡诱导与剪切湍流的气泡破碎、湍流相间扩散及传质模型[J]. 化工学报, 2022, 73(6): 2573-2588. SHI W B, LONG S S, YANG X G. Bubble breakage, turbulence dispersion and mass transfer model considering the joint effects of bubble-induced turbulence and shear turbulence[J]. CIESC Journal, 2022, 73(6): 2573-2588. |
| [17] |
张华海, 王悦琳, 李邦昊, 等. 湍流中气泡破碎建模与实验研究进展[J]. 化工学报, 2021, 72(12): 5936-5954. ZHANG H H, WANG Y L, LI B H. Review of bubble breakup modelling and experimental study in turbulent flow[J]. CIESC Journal, 2021, 72(12): 5936-5954. |
| [18] |
SOLSVIK J, JAKOBSEN H A. A review of the statistical turbulence theory required extending the population balance closure models to the entire spectrum of turbulence[J]. AIChE Journal, 2016, 62(5): 1795-1820. DOI:10.1002/aic.15128 |
| [19] |
SOLSVIK J, TANGEN S, JAKOBSEN H A. On the constitutive equations for fluid particle breakage[J]. Reviews in Chemical Engineering, 2013, 29(5): 241-356. |
| [20] |
COULALOGLOU C A, TAVLARIDES L L. Description of interaction processes in agitated liquid-liquid dispersions[J]. Chemical Engineering Science, 1977, 32(11): 1289-1297. DOI:10.1016/0009-2509(77)85023-9 |
| [21] |
MAO Z S, DUKLER A E. Rise velocity of a Taylor bubble in a train of such bubbles in a flowing liquid[J]. Chemical Engineering Science, 1985, 40(11): 2158-2160. DOI:10.1016/0009-2509(85)87039-1 |
| [22] |
YUAN J J, WENG Z H, SHAN Y G. Modelling of double bubbles coalescence behavior on different wettability walls using LBM method[J]. International Journal of Thermal Sciences, 2021, 168(6): 107037. |
| [23] |
CAZAREZ-CANDIA O, BENÍTEZ-CENTENO O C. Comprehensive experimental study of liquid-slug length and Taylor-bubble velocity in slug flow[J]. Flow Measurement and Instrumentation, 2020, 72: 101697. DOI:10.1016/j.flowmeasinst.2020.101697 |
| [24] |
张井志, 梁福顺, 黄楠燕, 等. 小管径圆管气-液界面可视化及含气率[J]. 高校化学工程学报, 2021, 35(2): 236-242. ZHANG J Z, LIANG F S, HUANG N Y. Visualization and void fraction of gas-liquid interfaces in minicircular tubes[J]. Journal of Chemical Engineering of Chinese Universities, 2021, 35(2): 236-242. DOI:10.3969/j.issn.1003-9015.2021.02.006 |
| [25] |
汪志能, 王晓川. 基于弹状流和搅拌流的气力提升泵建模[J]. 高校化学工程学报, 2021, 35(1): 42-50. WANG Z N, WANG X C. Model for airlift pumps based on slug-churn flow[J]. Journal of Chemical Engineering of Chinese Universities, 2021, 35(1): 42-50. |
| [26] |
CACHARD F D, DELHAYE J M. A slug-churn flow model for small-diameter airlift pumps[J]. International Journal of Multiphase Flow, 1996, 22(4): 627-649. |
| [27] |
MOHMMED A O, NASIF M S, AL-KAYIEM H H, et al. Measurements of translational slug velocity and slug length using an image processing technique[J]. Flow Measurement & Instrumentation, 2016, 50: 112-120. |
| [28] |
MOFFAT R J. Describing the uncertainties in experimental results[J]. Experimental Thermal and Fluid Science, 1988, 1(1): 3-17. |




