2. 杭州制氧机集团股份有限公司, 浙江 杭州 310014
2. Hangzhou Oxygen Plant Group Co. Ltd., Hangzhou 310014, China
在生产中,空分装置需要变负荷操作,以满足用户周期性、间歇性和阶段性变化的气体需求[1]。在保证产品合格的前提下,快速搜索满足控制弹性要求的最优经济操作点是空分研究的重要问题。
空分是低温装置,流程耦合性强,操作变量可行域小。对变负荷过程,要获得匹配负荷的最佳操作点,必须有准确的数学模型。李华银等[1]对空分变负荷系统建立动态数据模型,将模型预测用于现场控制。祝铃钰等[2]建立空分装置的机理模型,采用回溯同伦法求解变负荷运行的不同工况。但以上模型未对多股流换热器(MHEX)建立机理模型,无法描述扰动引起的误差。MHEX内部多个流股之间能同时进行换热,广泛应用于深冷空分装置,但存在结构复杂、建模困难等问题。Yee等[3]提出分级超结构建模方法(Stage-Wise,SW),同步优化换热面积、能耗和换热器个数。魏关峰等[4]参考Yee的超结构模型,用遗传算法求解换热器网络的综合问题。Hasan等[5]使用双流股换热器换热网络替换带相变的MHEX,预测变工况下的操作。所以,用SW超结构模型建立的等价换热网络模型能够准确描述MHEX,便于对过程进行操作分析。对于复杂装置,传统优化通常采用刚性的过程约束,这些约束可能是极端条件下的安全值,会降低系统的经济性。Swaney和Grossmann定义了弹性(Flexibility)[6],用于衡量过程系统对不确定参数变化的适应能力。引入弹性指数,可以在考虑装置的控制器精度下进行过程优化。白一媛等[7]考虑污垢生长的弹性优化换热网络,提出改善换热装置弹性的方法。沈颖达等[8]采用混合整数非线性优化,同时考虑换热网络弹性、控制性能与经济性的情况下进行换热网络旁路优化。因空分变负荷的过程复杂,建立与机理过程相匹配的代理模型可简化计算过程。Zhao等[9-11]提出用柱形代数分解(cylindrical algebraic decomposition,CAD)方法,通过量词消去,将多变量的高维解空间投影至弹性的一维空间上,得到边界的代理模型。
本研究提出一种基于空分设备操作域和控制器精度的优化策略,通过工业数据建立空分过程机理模型,将操作弹性边界代理化,便于控制器搜寻操作空间和最优操作点,为空分变负荷操作提供指导建议。
2 基于弹性分析的优化命题在空分变负荷操作中,需要改变设备的操作变量应对管网进料压力的改变。当氮气压力发生波动时,变负荷的设备操作弹性区域也会变化,增加操作难度。当压力发生改变时,确定空分设备变负荷操作的可行域,可为控制器提供一个参考范围,用以对流程进行较为精确的预测和控制;同时,通过确定最佳工作点,降低过程能耗和气体放散量,可使经济效益最大化。
为解决空分装置在变负荷过程中的弹性问题,本节将依据弹性指数定义优化命题,CAD被用于确定优化命题中约束的显式表达式。建立考虑弹性的变负荷操作优化命题,主要分为2个部分:
(1) 在Aspen中建立机理模型模拟生成可行域样本集。
(2) 根据样本集用CAD解析边界代理模型用于优化问题。
对于任意过程,存在等式约束h与不等式约束g:
| $ \left\{ \begin{gathered} h(d, z, \theta , x) = 0 \hfill \\ g(d, z, \theta , x) \leqslant 0 \hfill \\ \end{gathered} \right. $ | (1) |
式中:d、z、θ和x分别为表征设备固有属性的设计变量、过程控制变量、操作变量和状态变量。将等式约束
| $ D = \left\{ {\theta |\left[ {\exists z|f(d, z, \theta ) \leqslant 0} \right]} \right\} $ | (2) |
检验操作弹性的问题可以表述为:对于任意的θ∈T,至少存在一个控制变量z,使得模型满足可行域D。其中
| $ \forall \theta \in T\text{,}\theta \in D=\left\{\exists z\left(l\in L\left[{f}_{l}(d, z, \theta )\le 0\right]\right)\right\} $ | (3) |
其可转化为
| $ \mathop {{\text{max}}}\limits_{\theta \in T} \mathop {{\text{min}}}\limits_z \mathop {{\text{max}}}\limits_{l \in L} {f_l}\left( {d, z, \theta } \right) \leqslant 0 $ | (4) |
此时,操作弹性的检验可等价为判断χ(d)是否小于0。
| $ \chi \left( d \right) = \mathop {{\text{max}}}\limits_{\theta \in T} \mathop {{\text{min}}}\limits_z \mathop {{\text{max}}}\limits_{l \in L} {f_l}\left( {d, z, \theta } \right) $ | (5) |
当
对任意操作变量θ,存在其操作正则点集合N
| $ \begin{gathered} \mathop {{\text{max}}}\limits_\theta {\text{ Prof}} \\ {\rm{s.t.}}\left\{ \begin{array}{l} \mathop {{\text{max}}}\limits_{\theta \in T} \mathop {{\text{min}}}\limits_z \mathop {{\text{max}}}\limits_{l \in L} {f_l}\left( {d, z, \theta } \right) \leqslant 0 \hfill \\ T = \left\{ {\theta {\text{|}}\left( {{\theta ^N} - {\delta _{\rm{set}}}\Delta {\theta ^ - }} \right) \leqslant \theta \leqslant \left( {{\theta ^N}{\text{ + }}{\delta _{\rm{set}}}\Delta {\theta ^ + }} \right)} \right\} \hfill \\ \end{array} \right. \\ \end{gathered} $ | (6) |
式中:
|
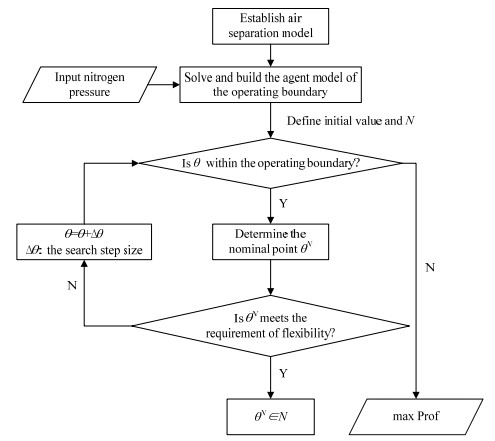
图 1 过程计算框图 Fig.1 Process calculation block diagram |
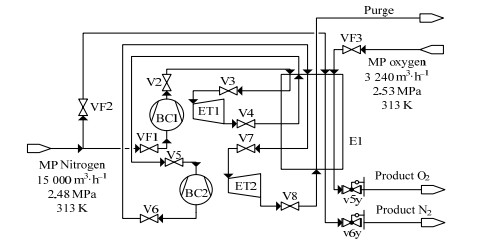
以某空分装置的氧氮液化流程为例,具体流程如图 2所示。
|
图 2 空分装置流程图 Fig.2 Flow chart of air separation unit |
温度为313 K、压力为2.48 MPa的中压氮气(压力在1.6~2.5 MPa间波动)自管网通入高温膨胀机压缩端BC1增压,进入多股流换热器E1的热端与返流气体换热。温度降至200 K后进入高温膨胀机ET1中膨胀,返回换热器E1的冷端换热升温至常温,再进入低温膨胀机压缩端BC2,增压后降温并进入高温膨胀机ET2中膨胀,返回换热器E1的冷端,最后换热至常压。生产液氮时,来自管网的标准状态下氮气总流量为15 000 m3⋅h−1,其中2 700 m3⋅h−1氮气直接换热液化,降温至81.1 K节流至约0.3 MPa作为全液相产品输出。
3.1 等价换热网络建立在空分的氧氮液化流程中含有多股流换热器、阀门、压缩机、混合器、膨胀机和分流器等。Aspen中的多股流换热器模块MHeatX存在一定的局限性,仅能通过确定出料流股的状态进行简单的热平衡计算。但是实际的操作分析中,多股流换热器的设备参数是确定的,需要建立多股流换热器的替代模型进行操作分析。将多股流换热器按冷热流股的进出口位置拆分多个级,每一级都能拆分成由数个换热节点组成的换热网络,其中每个节点都是单股热流和单股冷流换热。假定一个级内包含I股冷流和J股热流进料,则I股冷流中的每一股需拆分成J股和热流换热;同样的,J股热流中的每一股也需拆分成I股和冷流换热。假设模型满足:
(1) 每股冷流和每股热流都换热。
(2) 每一级的出口截面上所有冷流和热流出口温度相等。
Aspen中的双流换热器模块HeatX可用于设计、确定换热面积等参数;也可在确定参数下操作分析。因此用双流换热器建立的等价多级换热网络,能够在Aspen中实现空分流程的操作分析。
3.2 CAD辅助确定操作边界柱形代数分解是由Collins[12]提出的一种用于量词消去的符号计算方法。CAD可以将一个实数空间Rn (在给定的变量顺序下,
将一组n元多项式系统
| $ \begin{array}{l} {F^n} \subset {{\bf R}^n} = \left\{ {{x_1}, {x_2}, ..., {x_{n - 1}}, {x_n}} \right\} \hfill \\ {F^{n{\text{ - }}1}} \subset {{\bf R}^{n{\text{ - }}1}} = \left\{ {{x_1}, {x_2}, ..., {x_{n - 1}}} \right\} \hfill \\ ... \hfill \\ {F^2} \subset {{\bf R}^2} = \left\{ {{x_1}, {x_2}} \right\} \hfill \\ {F^1} \subset {{\bf R}^1} = \left\{ {{x_1}} \right\} \hfill \\ \end{array} $ | (7) |
使用Aspen灵敏度分析模块得出操作变量在一定变化范围生成的可行域样本集,基于初始样本集建立不等式约束模型。通过CAD方法,获得具有显式表达式的弹性区域,并对边界进行细化,得到较为精确的弹性操作边界代理模型。
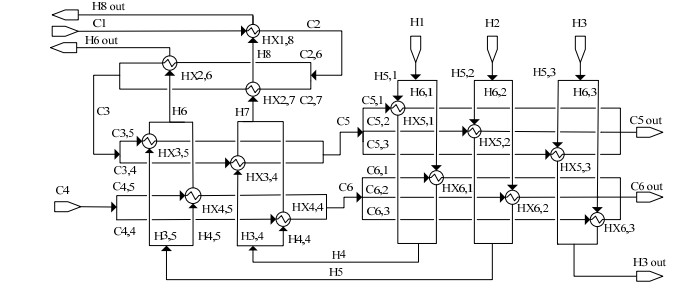
4 基于产品液化最大的空分变负荷最佳操作优化 4.1 等价换热网络模型和参数估计以SW法拆分主换热器E1,按冷热流股的出口位置分成4级,每级截面温度的初值通过流股的比热容和简单的质量衡算粗略计算获得,再对4个子换热器进行精确的模拟计算, 将其拆分成简单的换热网络。每股冷流拆成J股,编号为C(i, j);每股热流拆成I股,编号为H(i, j);对任意热流j和任意冷流i,在换热器HX(i, j)交换热量。E11包含了3个热流股和2个冷流股,故拆分为6个双流换热器所构成的换热网络,E12可拆分成4个换热器,E13可拆分成2个换热器,E14仅一个换热器。综上,多股流换热器E1的等价换热网络由13个双流换热器组成,如图 3所示。
|
图 3 等价换热网络结构 Fig.3 Equivalent heat exchangers network structure |
用换热网络替换多股流换热器后,流程共有11个分流器、10个混合器、13个双流股换热器、2个压缩机和2个膨胀机。以空分现场工况为设计点,进行换热器和分流器的参数估计,假定换热器的换热效率为常数,无压降,换热器面积和流股分流比例如表 1所示。其余设备参数无需估算。
|
|
表 1 设备参数表 Table 1 Equipment parameters |
根据表 1中的设备参数,在Aspen中用等价换热网络替换多股流换热器建立流程,其在不同工况点下的模拟结果与使用MHeatX的流程相对比,流股和温度压力数据最大误差在±2.5% 以内,平均相对误差为0.3%。这表明该设计方案可行,等价换热网络构建完成。
4.2 变负荷操作变量和操作边界对Aspen搭建的空分流程进行操作分析,可调工艺设定值共11个,其中考虑管网氮气进料的温度和流量不变,仅压力发生波动;普通阀门压降为0,减压阀出口压力由产品要求决定;设备参数通过估计得到,膨胀机和压缩机的功关联,所以仅考虑膨胀机的出口压力即可。模型可调变量为4个,分别为氮气进料压力、氮气分流量、2个膨胀机出口压力。当进料氮气流量和温度不变时,氮气进料压力波动会影响氮气分流量,此时还需要调整膨胀机出口压力实现优化操作。本研究以氮气分流量作为经济指标建立操作优化命题。
在空分变负荷操作中,来自管网的氮气压力会在1.6 ~2.5 MPa波动。对应这个扰动操作变量,需要调节氮气分流量qV (m3⋅h−1)和膨胀机ET1、ET2的出口压力pET1(MPa)、pET2(MPa),在设备能力允许范围内将qV全部液化。所有符合上述要求的qV和pET1、pET2集合即为某一氮气压力扰动下的操作可行域。本研究作只考虑产品量为目标,此时优化命题为求满足弹性要求的最大氮气分流量。
| $ \begin{gathered} \mathop {\max }\limits_{{\theta _2}, {\theta _3}, {\theta _4}} {\text{ }}{\theta _2}^N \\ {\rm{s.t.}}\left\{ \begin{array}{l} \mathop {\max }\limits_{\theta \in T} \mathop {\min }\limits_z \mathop {\max }\limits_{l \in L} {f_l}\left( {d, z, \theta } \right) \leqslant 0 \hfill \\ T = \left\{ {\theta {\text{|}}\left( {{\theta ^N} - {\delta _{\rm{set}}}\Delta {\theta ^ - }} \right) \leqslant \theta \leqslant \left( {{\theta ^N}{\text{ + }}{\delta _{\rm{set}}}\Delta {\theta ^ + }} \right)} \right\} \hfill \\ \end{array} \right. \\ \end{gathered} $ | (8) |
过程的等式约束由内部的平衡方程决定,不等式约束由现场工况和设备要求给出。对于该流程,存在以下不等式约束(因膨胀机和压缩机的功在流程中关联,故只需约束膨胀机的操作条件):
(1) 膨胀机的操作功保持在标准工况的±20% 内。
(2) 膨胀机ET1功率与膨胀机ET2功率之比在0.8~1.2。
(3) 产品流股必须为液相,等价为产品流股的焓值不大于其泡点温度下的焓值。
(4) 氮气管网进料负荷波动
(5) 氮气分流流量
(6) 膨胀机出口压力不低于大气压,且设备要求出口压力最大范围在设计工况的±40% 以内。其中膨胀机ET1出口压力pET1(
状态变量
| $ \left\{ \begin{array}{l} 0.8 \leqslant {g_1} = {W_{\rm{ET1}}}/W_{\rm{ET1}}^* \leqslant 1.2{\text{ , }}0.8 \leqslant {g_2} = {W_{\rm{ET2}}}/W_{\rm{ET2}}^* \leqslant 1.2 \hfill \\ {g_3} = {W_{\rm{ET1}}} - 1.2{W_{\rm{ET2}}} \leqslant 0{\text{ }}, {\text{ }}{g_4} = {W_{\rm{ET1}}} - 0.8{W_{\rm{ET2}}} \geqslant 0 \hfill \\ {g_5} = {H_N} - H_N^* \leqslant 0 \hfill \\ 1.6 \leqslant {\theta _1} \leqslant 2.5 \hfill \\ 2{\text{ }}000 \leqslant {\theta _2} \leqslant 3{\text{ }}400 \hfill \\ 0.7 \leqslant {\theta _3} \leqslant 1.4{\text{ }}, {\text{ }}0.1 \leqslant {\theta _4} \leqslant 0.18 \hfill \\ \end{array} \right. $ | (9) |
通过给定不同的
| $ \begin{array}{l} \left\{ \begin{array}{l} {f_1}({\theta _2}, {\theta _3}, {\theta _4}) = 120.737 - 0.235{\text{ }}634{\theta _2} + 0.000{\text{ }}032{\text{ }}080{\text{ }}8{\theta _2}^2 + 111.776{\theta _3} - 0.000{\text{ }}621{\text{ }}963{\theta _2}{\theta _3} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1.656{\text{ }}65{\theta _3}^2 - 1{\text{ }}040.1{\theta _4} + 0.337{\text{ }}18{\theta _2}{\theta _4} - 81.868{\text{ }}6{\theta _3}{\theta _4} + 808.591{\theta _4}^2 \hfill \\ {f_2}({\theta _2}, {\theta _3}, {\theta _4}) = 2{\text{ }}090.66 - 1.429{\text{ }}03{\theta _2} + 0.000{\text{ }}225{\text{ }}854{\theta _2}^2 + 233.036{\theta _3} - 0.131{\text{ }}639{\theta _2}{\theta _3} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;50.775{\text{ }}1{\theta _3}^2 - 6{\text{ }}244.26{\theta _4} + 2.291{\text{ }}88{\theta _2}{\theta _4} - 644.392{\theta _3}{\theta _4} + 4{\text{ }}314.82{\theta _4}^2 \hfill \\ {f_3}({\theta _2}, {\theta _3}, {\theta _4}) = 64{\text{ }}594.1 - 44.458{\text{ }}3{\theta _2} + 0.007{\text{ }}529{\text{ }}59{\theta _2}^2 + 10{\text{ }}020{\theta _3} - 3.845{\text{ }}13{\theta _2}{\theta _3} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1{\text{ }}484.59{\theta _3}^2 - 205{\text{ }}915{\theta _4} + 74.394{\text{ }}8{\theta _2}{\theta _4} - 22{\text{ }}288.3{\theta _3}{\theta _4} + 155{\text{ }}738{\theta _4}^2 \hfill \\ {f_4}({\theta _2}, {\theta _3}, {\theta _4}) = - 1{\text{ }}551.79 + 0.907{\text{ }}591{\theta _2} - 0.000{\text{ }}148{\text{ }}602{\theta _2}^2 - 74.653{\text{ }}4{\theta _3} + 0.104{\text{ }}69{\theta _2}{\theta _3} - \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;38.963{\text{ }}4{\theta _3}^2 + 3{\text{ }}955.31{\theta _4} - 1.496{\text{ }}33{\theta _2}{\theta _4} + 433.645{\theta _3}{\theta _4} - 2{\text{ }}643.27{\theta _4}^2 \hfill \\ {f_5}({\theta _2}, {\theta _3}, {\theta _4}) = - 2{\text{ }}388.05 + 1.479{\text{ }}2{\theta _2} - 0.000{\text{ }}238{\text{ }}943{\theta _2}^2 - 167.868{\theta _3} + 0.157{\text{ }}345{\theta _2}{\theta _3} - \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;59.273{\text{ }}4{\theta _3}^2 + 6{\text{ }}453.01{\theta _4} - 2.413{\text{ }}08{\theta _2}{\theta _4} + 691.402{\theta _3}{\theta _4} - 4{\text{ }}369.19{\theta _4}^2 \hfill \\ \end{array} \right. \hfill \\ {\text{ }} \hfill \\ \end{array} $ | (10) |
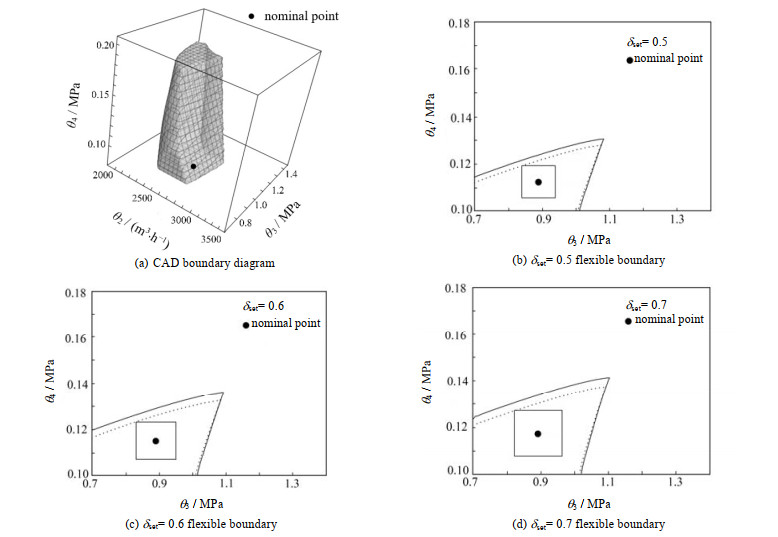
考虑液氮分流量和膨胀机出口压力对过程影响大小和控制器的精度不同,根据现场工况,要求操作变量θ2、θ3、θ4偏差Δθ+和Δθ−分别为±27 m3⋅h−1、±0.1 MPa、±0.014 MPa;要求最小弹性指数
|
图 4 弹性边界代理模型 Fig.4 Surrogate model of flexible boundary |
|
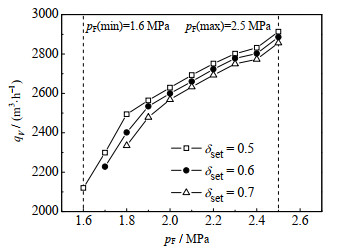
图 5 不同操作弹性下的优化结果 Fig.5 Optimization results under different operating flexibility |
由图 5可知,若在变负荷中需要操作变量存在较大的弹性空间,则氮气的最大液化量会相应地减少,即控制器的控制精度能决定变负荷的最优操作点。控制精度改变时,最优氮气液化量改变,同时系统能接受的压力扰动也会改变。在较低氮气进料压力时,控制器精度改变对变负荷最优操作点的影响较大。
5 结论为解决空分变负荷过程复杂,操作可行域小而难以控制的问题,基于CAD方法和弹性分析,提出一种求解变负荷操作优化命题的方法。该方法分为三步进行:(1) 建立SW超结构换热网络等价替换多股流换热器,进而建立空分装置机理模型,用以操作分析;(2) 以CAD方法处理样本集,得到弹性边界关于操作变量的显式表达式;(3) 基于操作弹性建立空分过程的优化命题,用以分析控制器精度和范围对操作的影响。通过对氮气液化工况的计算,获得操作精度与最优操作点的关系,验证了方法的可行性,为空分变负荷操作在满足经济的前提下稳定运行提供指导意见。
| [1] |
李华银, 赵均, 徐祖华. 多变量预测控制在空分装置自动变负荷中的应用[J]. 化工自动化及仪表, 2009, 36(4): 64-67. LI H Y, ZHAO J, XU Z H. Application of multi-variable model predictive control to automatic variable-loading of air separation unit[J]. Control and Instruments in Chemical Industry, 2009, 36(4): 64-67. |
| [2] |
祝铃钰, 陈智强, 陈曦, 等. 大规模变工况流程模拟的回溯同伦法[J]. 高校化学工程学报, 2009, 23(4): 690-695. ZHU L Y, CHEN Z Q, CHEN X, et al. Homotopy based backtracking method for large-scale process simulations with load Variation[J]. Journal of Chemical Engineering of Chinese Universities, 2009, 23(4): 690-695. |
| [3] |
YEE T F, GROSSMANN I E, KRAVANJA Z. Simultaneous optimization models for heat integration—I. Area and energy targeting and modeling of multi-stream exchangers[J]. Computers & Chemical Engineering, 1990, 14(10): 1151-1164. |
| [4] |
魏关锋, 姚平经, 罗行, 等. 用遗传算法进行多流股换热器网络综合的研究[J]. 高校化学工程学报, 2003, 17(4): 425-430. WEI G F, YAO P J, LUO X, et al. Study on multi-stream heat exchanger networks synthesis with genetic algorithm[J]. Journal of Chemical Engineering of Chinese Universities, 2003, 17(4): 425-430. |
| [5] |
HASAN M M F, KARIMI I A, ALFADALA H E, et al. Operational modeling of multistream heat exchangers with phase changes[J]. AIChE Journal, 2009, 55(1): 150-171. DOI:10.1002/aic.11682 |
| [6] |
SWANEY R E, GROSSMANN I E. An index for operational flexibility in chemical process design. Part Ⅰ: Formulation and theory[J]. AIChE Journal, 1985, 31(4): 621-630. DOI:10.1002/aic.690310412 |
| [7] |
白一媛, 刘琳琳, 顾偲雯, 等. 考虑污垢生长的柔性换热器网络综合[J]. 高校化学工程学报, 2018, 32(4): 926-932. BAI Y Y, LIU L L, GU S W, et al. Synthesis of flexible heat exchanger network with fouling growth[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(4): 926-932. |
| [8] |
沈颖达, 孙琳, 罗雄麟. 低灵敏度换热网络的旁路优化设计[J]. 西安交通大学学报, 2017, 51(4): 142-148. SHEN Y D, SUN L, LUO X L. Bypass optimal design of heat exchanger networks with low sensitivity[J]. Journal of Xi'an Jiaotong University, 2017, 51(4): 142-148. |
| [9] |
ZHAO F, ZHENG C, ZHANG S, et al. Quantification of process flexibility via space projection[J]. AIChE Journal, 2019, 65(10): e16706. |
| [10] |
ZHAO F, CHEN X. Analytical and triangular solutions to operational flexibility analysis using quantifier elimination[J]. AIChE Journal, 2018, 64(11): 3894-3911. |
| [11] |
ZHENG C, ZHAO F, ZHU L, et al. Operational flexibility analysis of high-dimensional systems via cylindrical algebraic Decomposition[J]. Industrial & Engineering Chemistry Research, 2020, 59(10): 4670-4687. |
| [12] |
COLLINS G E. Quantifier elimination for real closed fields by cylindrical algebraic decomposition[J]. Lecture Notes in Computer Science, 1975, 33: 134-183. |
| [13] |
朱章鹏, 陈长波. 基于机器学习的柱形代数分解变元择序[J]. 系统科学与数学, 2020, 40(8): 1492-1506. ZHU Z P, CHEN C B. Varible ordering selection for cylindrical algebraic decomposition based on machine learning[J]. Journal of Systems Science and Mathematical Sciences, 2020, 40(8): 1492-1506. |




