两相流的相界面,即流型形态,具有重要的意义。例如,对于气液两相的化学气泡反应柱或液固两相的浆体输送管道,其相关的流动形态对成本核算、质量监测均具有指导作用[1-3]。为获得颗粒两相流的截面分布,电阻层析成像(ERT, electrical resistance tomography)、电容层析成像(ECT,electrical capacitance tomography)以及超声过程层析成像(UPT, ultrasonic process tomography)得到了发展。近几年来,电学法已经比较成熟,并在多相成分测量中取得了许多成功的应用[4-6]。但是,与电学法相比,超声过程层析成像不受软场效应影响、适用高浓度条件测量,因此已有不少针对透射或反射式超声方法的研究[7-9]。为了增加投影信息量,发散角大于150°的扇形束扫描常会被用到两相体系检测中以扩大检测范围。此外,多模态层析成像技术也为增加投影信息量,提高重建效果提供了新的思路,并在近年得到了较多关注[10-11]。它通过集成不同类型的传感器以更精确地描述被测对象。目前,电学等方法结合超声技术的多模态成已逐渐发展到颗粒两相流领域[12]。但是,其亦遇到诸多困难,在不同原理的系统集成、数据同步采集和数据处理中尤为明显。
对反射信号的测量,小尺寸换能器是保证渡越时间(TOF, time of flight)准确测量的重要条件。在基于反射式超声过程层析成像的研究中[13-14],典型的发射器工作表面为平面,其产生波束发散角不及90°。因此,反射式UPT的测量敏感区域达不到整个截面,投影信息量受限;对于透射模式UPT,已有使用柱面PZT(锆钛酸铅)压电元件(其发射面宽大于10 mm)[15],但是透射式成像系统很难获得小于10 mm的颗粒重建图像。另外,在透射模式的重建算法方面,Faramarzi等人[16]采用不同滤波方式的卷积反投影(CBP, convolution back projection)算法和线性反投影(LBP,linear back projection)算法对重建图像的质量进行了对比,发现CBP算法具有较好的应用前景。但是,上述算法未能很清晰地反映颗粒系中尺寸较小的颗粒。因此,本文提出一种超声双模式(透射和反射模式)检测和数据融合方法,在提高投影数据量和降低系统集成难度间取得均衡。为同步获取具有足够精度的超声透射和反射信号,双模式UPT系统需考虑柱面换能器小型化。相比于PZT,聚偏氟乙烯(PVDF)材料具有非常好的柔韧性(易弯曲),非常利于对超声波透射和反射信号同步测量有要求的双模式超声成像。然后,发展融合超声波透射和反射数据的图像重建算法,提高颗粒形态重建质量。
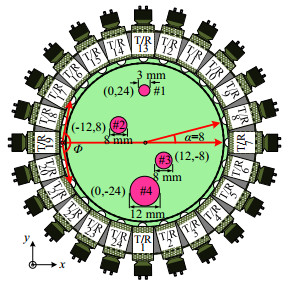
2 UPT系统声场仿真 2.1 阵列区声场特征考虑到反射法需要满足声波经过颗粒时能产生较为明显的反射现象,因此选用了颗粒材质满足声阻抗特性与背景相(水)具有明显差异的钢珠颗粒。图 1给出了阵列结构模型和样品空间分布,其中测试区为直径D = 80 mm的圆管截面结构,内部置水。传感器阵列包括24个呈15°均匀布置的超声波换能器,其编号沿逆时针方向依次为T/R1~T/R24。设定最小被测颗粒的尺寸接近于换能器的发射表面宽度,其原因与下文分析的颗粒尺寸测量下限有关。
|
图 1 超声层析成像阵列结构和颗粒样品 Fig.1 Schematic diagram of the ultrasonic tomography configuration and particle samples |
为了直观地描述双模式超声层析成像测量原理,需对定义层析成像系统的声学特性进行数值分析。声波动方程可简化为非齐次亥姆霍兹方程[17]:
| $ \nabla \cdot \left( { - \frac{1}{\rho }\left( {\nabla p - \mathit{\boldsymbol{q}}} \right)} \right) - \frac{{{\omega ^2}p}}{{\rho {c^2}}} = \mathit{\boldsymbol{Q}} $ | (1) |
其中:p (Pa)是液相或固相中的声压;ρ (kg·m-3)是对应相密度;c (m·s-1)是对应相中声速。声源偶极子q (N·m-3)和单极子Q (1·s-2)忽略,而是采用了柱面声源(位于T/R19处);边界上施加辐射边界条件[18],吸收柱面波。柱面波声源是以连续波的形式沿x轴传播,其幅值Ain可表示为:
| $ {A_{{\rm{in}}}} = \frac{{\rm{j}}}{4} \times [J(0, {k_{\rm{w}}}{R_{\rm{s}}}) - {\rm{j}} \times Y(0, {k_{\rm{w}}}{R_{\rm{s}}})] $ | (2) |
式中:Rs代表检测区域的任意一点到声源T/R19的距离;kw = 2πf/cw表示水中的波数;f为超声频率,设为4 MHz;函数J和Y分别表示第一类和第二类的贝塞尔函数;j是虚数部分。
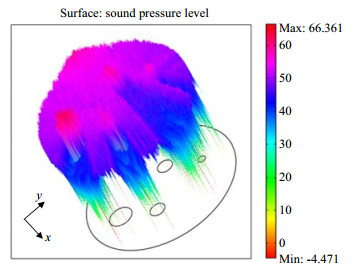
声场模拟基于COMSOL仿真软件,结果以声压级分布显示(如图 2)。可见每一颗粒均对超声波存有明显的遮挡,形成阴影区;同时声波散射非常微弱,符合几何近似要求。此外,由于存在超声反射现象,在颗粒后方的声影区声压级呈现非均匀分布,反射波能量明显小于透射波。按照声压级SPL定义:
| $ {\rm{SPL}} = 20 \times {\rm{lg}}(p/{p_{{\rm{ref}}}}) $ | (3) |
|
图 2 四个不同颗粒的声压级图(单位:dB) Fig.2 Sound pressure level of four different particles (Unit: dB) |
其中:p为目标声压,pref为参考声压。对比可以看出,声源处和颗粒后阴影区的声压级相差30 dB,即ΔSPL = 30 dB。通过声衰减系数的定义:α = (p1-p2)/p1,(p1,p2分别为声源处和颗粒背后处的目标声压),透射波经过钢珠颗粒时能量衰减了约97%。
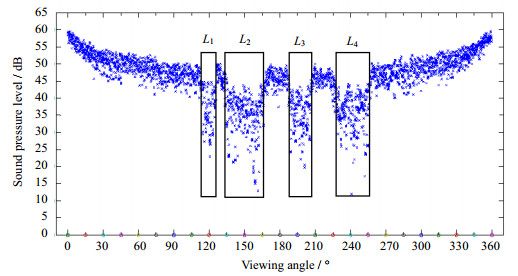
2.2 颗粒尺寸测量下限提取成像区边缘附近网格的声压级,得到不同观测角度下的声波强度。如图 3所示,矩形宽度代表了几何声影宽度L。由于声影表示颗粒遮挡的透射波,所以声影需完全覆盖接收换能器工作面才可感知颗粒是否存在,即L > l (l为换能器发射面宽度)。L1,L2,L3,L4分别表示由#1,#2,#3和#4颗粒引起的声影宽度。从图 3分析可得:L3 < L2;L1 < L4。#2和#3颗粒尺寸相同,且#2颗粒更靠近发射器。由L3 < L2可推知:同尺寸颗粒,越远离发射器,声影越窄;同理,由L1 < L4可推知:离发射器距离相同,颗粒尺寸越小,声影越窄。综上可知最窄声影是由边缘处的小颗粒决定,且可近似认为L = d (d为边缘处最小颗粒直径)。且由上述条件L > l,可以得到d > l。表明颗粒尺寸的测量下限原则上应大于换能器发射面宽度,为此文中选用的最小颗粒尺寸略大于换能器发射面宽度。
|
图 3 T/R19为发射器时声压级随观测角变化 Fig.3 Profile of sound pressure level as a function of viewing angle (T/R19 as the transmitter) |
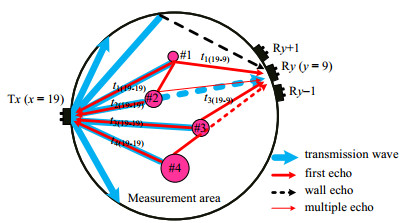
声场特征表明了声波散射非常微弱,符合几何近似要求。如图 4所示,透射波以直线传播方式通过介质,首先到达对面接收器,形成的反射波遵守表面反射原理[19]。透射波经某颗粒反射后称为一次回波。图 4中三种不同的虚线箭头分别表示透射波被颗粒#2遮挡后能量大幅衰减,管壁面反射波被抑制和一次回波在传播过程中受到颗粒#3遮挡。多次反射波可能带来干扰,影响可用信息提取。但经历一次以上反射的回波能量已经耗散。另外,内壁面的反射波需要抑制。通过在换能器的工作端表面(除发射/接收面)附有丁基橡胶吸声材料,可以有效抑制和减轻壁面反射影响(如图 5),可近似认为是吸收边界。
|
图 4 射线理论下的透射波和反射波路径示意图 Fig.4 Schematic diagram of transmission and reflection paths under the ray theory |
|
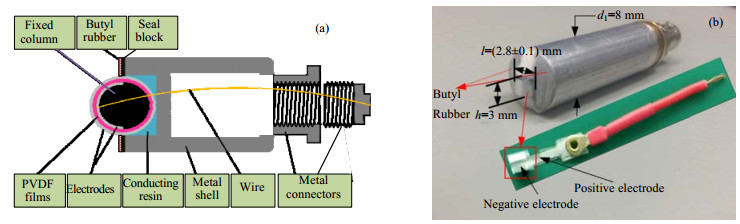
图 5 PVDF换能器的构造设计图(a)及其实物图(b) Fig.5 Structural design of the PVDF transducer (a) and item picture (b) |
对于透射模式UPT而言,需要采集的有效信号为扇形声束到达每个接收换能器的透射波信号;而反射式UPT重建则需利用透射波与颗粒作用所产生的一次回波信号。为确保在扫描过程中各通道间互不影响,一次发射间隔时间需保证数据采集完成,并且成像区内超声波在下一次发射前完全耗散消失。对管径为D的测量区域和介质中的声速cw,超声波耗散最短时间间隔t (也称为扫描中最短间隙时间)可表示为:
| $ t{\rm{ = }}\frac{{2 \times D}}{{{c_{\rm{w}}}}} $ | (4) |
在本研究中,该最短时间间隔约为0.107 ms。此外,在双模式UPT中需要区分透射和反射超声信号。当两个相邻传感器之间的角α和管径D固定后,每条投影路径上理论的透射波声程D(Tx-Ry) (x ≠ y)可以预设:
| $ \left\{ \begin{array}{l} {D_{{\rm{(T}}x - {\rm{R}}y)}}{\rm{ = }}\sqrt {2 \times {{\left( {\frac{D}{2}} \right)}^2} \times \left[ {1 - {\rm{cos}}\left( {z \times \alpha } \right)} \right]} {\rm{ }}\\ \left| {x - y} \right| = z\;\;\;{\rm{ or }}\;\;\;\left| {x - y} \right| = {\rm{24}} - z \end{array} \right. $ | (5) |
式中,z的取值范围是{1, 2, 3, ……, 12}。采用门技术(range-gating)事先覆盖整个透射波区域,其主要目的是“套住”透射波并获取峰值信息。自发自收式换能器采集的一次回波长度2D;而一发一收式换能器其处理长度为[2D-D(Tx-Ry)],即从透射波之后的信号中进行判断并提取出一次回波的TOF值。
3.2 实验装置传感器的结构设计如图 5(a)所示。两个正负银电极之间的PVDF膜厚度约为28 μm。其中,外电极是与换能器金属外壳相连的圆柱形表面;内部电极为半圆柱形,以避免发射表面后方产生的复杂声场带来干扰。除了PVDF膜之外,在换能器的发射端面,采用丁基橡胶层以吸收成像区内余波。图 5(b)为换能器的实物图,发射面宽度l为(2.8±0.1) mm,发射面高度h为3 mm,换能器壳体的外径d1为8 mm。
实验成像区为图 6(a)所示内径80 mm、长度200 mm的管。实验中使用钢珠颗粒分布参数(如图 6(b))与数值模拟一致。核心部件24通道数字超声系统集成了三块8通道模块,各通道之间能同步收/发信号以及自动切换,以激励并控制24个传感器实现自动扇形束扫描。透射波的峰值和回波渡越时间通过数据处理程序提取后按照Tx-Ry的编号发送至主机,作为一系列的原始数据供代入图像重建算法。

|
图 6 超声层析成像装置图(a)及四钢珠样品体系图(b) Fig.6 Images of the ultrasonic tomography setup (a) and four steel ball samples (b) |
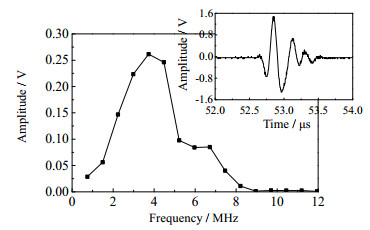
图 7为T/R19发射R7接收的透射波时域信号和对应的幅度谱(未加入钢珠时)。可以看出PVDF换能器激发频率为4 MHz。之前的研究表明[7-9],当被测颗粒的尺寸在毫米级时,该超声频率是合适的。为实现快速运算,透射波信号峰值转换成逻辑值。对实验数据,透射信号矩阵如下:
| $ {\mathit{\boldsymbol{S}}^{\rm{T}}}_{{\rm{(T}}x{\rm{ - R}}y{\rm{)}}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 1, \\ 0, \end{array}&\begin{array}{l} {V_{_{{\rm{(T}}x - {\rm{R}}y{\rm{)}}}}} \ge {V_{{\rm{th}}}}\\ {V_{_{{\rm{(T}}x - {\rm{R}}y{\rm{)}}}}} \le {V_{{\rm{th}}}} \end{array} \end{array}} \right. $ | (6) |
|
图 7 PVDF换能器的时域信号和频谱特征 Fig.7 Time domain signal and frequency spectrum characteristics of the PVDF transducer |
其中:V(Tx-Ry)是Tx-Ry投影路径上,经过颗粒的衰减信号幅值与背景值之比,取值在0到1之间。Vth是信号二值化的阈值。与此对应,射线理论模拟通过直线传播路径上有无钢珠颗粒来判断透射信号有无。COMSOL模拟则通过图 3所示声场,将完全位于声影区的接收器信号置0,否则为1。
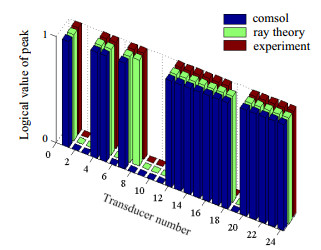
图 8中选取了T/R19发射,其它传感器接收的背景信号。由于T/R19自身为发射器,所以图中编号19处空缺。总体来说,三者的吻合度较好。对比射线理论和COMSOL数值仿真,实验数据反映出临近发射器的R18传感器未能接收到有效信号。原因在于大角度下声信号相对微弱,且换能器接收灵敏度特性存有差异。为了克服这个问题,如果背景信号中透射波强度小于噪音水平(即发散超声波难以到达该接收器),在该路径形成透射信号逻辑值被置为1,即认为是检测盲区。
|
图 8 三种方式获得的透射波峰逻辑值 Fig.8 Logical values of transmission peak obtained with three methods |
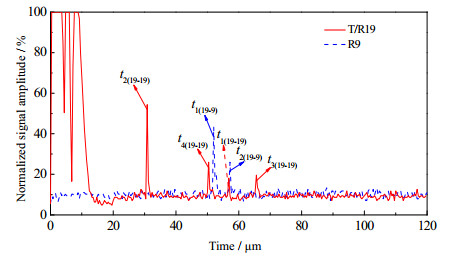
对反射信号,选取了如图 4所示的T/R19-R9投影路径实验信号。其中,ti(19-19)是第i号颗粒对应的19号换能器为发射器并同时作为接收器的回波信号渡越时间;ti(19-9)是第i号颗粒对应的19号换能器作为发射器、9号作为接收器的回波信号渡越时间。波形压缩技术被用来更好地存储、加快扫描和分析[20]。图 9显示了T/R19和R9接收到的一次回波信号,其性噪比良好(增益为92 dB),信号并没有受到多次回波和壁面反射波的干扰。
|
图 9 T/R19与R9接收到的信号 Fig.9 Compacted signals received by T/R19 and R9 |
典型的透射或者反射式二值线性反投影算法是二值Hybird重建算法[21]的一种修正形式。需分别定义标准化敏感系数矩阵MT和MR,双模式融合算法以二者为基础,进一步发展得:
| $ \begin{array}{l} \mathit{\boldsymbol{V}}(m, n) = \sum\limits_{x = 1}^{24} {\sum\limits_{y = 1(y \ne x)}^{24} {\left\{ \begin{array}{l} [1 - {\mathit{\boldsymbol{S}}^{\rm{T}}}_{{\rm{(T}}x{\rm{ - R}}y{\rm{)}}}] \times [{\mathit{\boldsymbol{M}}^{\rm{T}}}_{{\rm{(T}}x{\rm{ - R}}y{\rm{)}}}(m, n)\\ \cap {\mathit{\boldsymbol{M}}^{\rm{R}}}_{{{{\rm{(}}{S^{\rm{R}}}_{i{\rm{(T}}x{\rm{ - T}}x{\rm{)}}}{\rm{)}}}_{\min }}}(m, n)] \end{array} \right\}} } \\ \;\;\;\;\;\; \;\;\; \;\;\; \;\;\; + \sum\limits_{x = 1}^{24} {\sum\limits_{i = 1}^{{N_{{\rm{(T}}x{\rm{ - T}}x{\rm{)}}}}} {{\mathit{\boldsymbol{M}}^{\rm{R}}}_{i{\rm{(T}}x{\rm{ - T}}x{\rm{)}}}(m, n)} } \end{array} $ | (7) |
其中:V(m, n)是双模重建图像的权重分布;m和n表示200×200像素的节点坐标。透射信号矩阵ST和反射SR可以通过实验获得。N(Tx-Tx)是发射换能器Tx接收一次回波数。上式第一项表示双模式算法的去噪作用,而后一项强调了对检测颗粒的边界增强。
单模式和双模式UPT重建过程如图 10所示,透射法重建使用三角形法则,反射法选弧形法[22]。双模式融合算法的重建流程包括了敏感矩阵
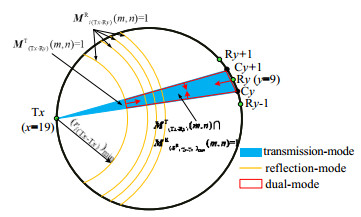
|
图 10 单模式、双模式重建过程示意图 Fig.10 Reconstruction processes of single-mode and dual-mode UPT |
读取信号矩阵S(Tx-Ry)T;
● 如果x = y,执行下一步;
● 如果x ≠ y且S(Tx-Ry)T = 1,执行下一步;
● 如果x ≠ y且S(Tx-Ry)T = 0,读取反射信号SR。对自发自收换能器接收的所有TOF数据搜索最小值,确定颗粒系外轮廓定位圆弧,该圆弧半径为:
| $ {({r_{i{\rm{(T}}x{\rm{ - T}}x{\rm{)}}}})_{{\rm{min}}}} = \frac{1}{2} \times {({\mathit{\boldsymbol{S}}^{\rm{R}}}_{i{\rm{(T}}x{\rm{ - T}}x{\rm{)}}})_{{\rm{min}}}} \times {c_{\rm{w}}} $ | (8) |
● 检测区中与该自发自收换能器距离大于
● 所有圆弧累加权重。由于透射法重建采取的三角形法则的单位网格权重M(Tx-Ry)T(m, n)为1,为平衡由发射器本身接收TOF圆弧在叠加时权重影响,弧形投影单位权重Mi(Tx-Tx)R(m, n)被置为NT/NR,其中NT和NR为有效透射和反射信号数。
5.2 重建结果分析将处理后实验信号带入不同UPT算法重建,获得如图 11所示的强度图像,发现其中或多或少存有噪影。相比单模式结果,双模式算法消除了颗粒整体轮廓外部噪影,颗粒系形态更清晰。对强度图像采取最优二值化分割[22],得图 12所示二值图像。图中可见,透射法对尺寸接近发射宽度的颗粒很难分辨;反射法中颗粒轮廓未能完全封闭,大颗粒封闭性较差。其主要原因是弧形反投影通过弧线加深颗粒轮廓,对小颗粒相对明显。双模式则结合了透射法易封闭的特点和反射法在轮廓加深的优势,兼顾了小颗粒识别和大颗粒封闭两个问题,更好地反映了颗粒实际形态。
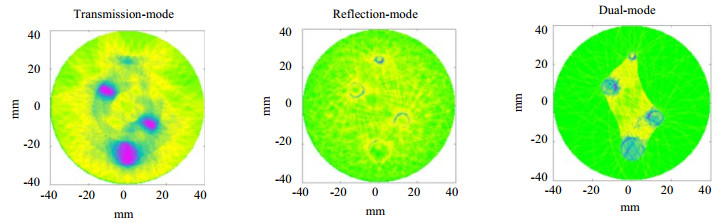
|
图 11 不同方法重建的强度图像 Fig.11 Reconstructed original intensity images obtained with different methods |

|
图 12 不同方法重建的二值图像 Fig.12 Reconstructed binary images obtained with different methods |
针对弧形反投影对反射和双模式重建可能造成的不封闭以及内部空隙问题,通过边缘连接构成连通域后填充。图 13为处理后封闭颗粒图像,综合分析三种模式封闭颗粒图像,发现重建颗粒在尺寸、形状及位置上和实验值存有差异。为量化重建方法成像精度,对200×200网格图像定义空间成像误差SIE和均方根误差RMSE:
| $ {\rm{SIE}} = \frac{{\sum\limits_{m = 1}^{200} {\sum\limits_{n = 1}^{200} {\left| {{G_{\rm{s}}}(m, n) - {G_{\rm{r}}}(m, n)} \right|} } }}{{\sum\limits_{m = 1}^{200} {\sum\limits_{n = 1}^{200} {{G_{\rm{s}}}(m, n)} } }} $ | (9) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{{{{200}^2}}}\sum\limits_{m = 1}^{200} {\sum\limits_{n = 1}^{200} {{{[{G_{\rm{s}}}(m, n) - {G_{\rm{r}}}(m, n)]}^2}} } } $ | (10) |
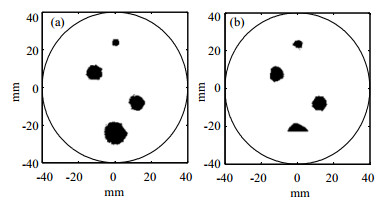
|
图 13 双模式法(a)和反射法(b)的填充结果 Fig.13 Filled images obtained with dual-mode (a) and reflection-mode (b) |
其中,Gs为重建图像权重值矩阵,Gr为真实图像的权重值矩阵。表 1是对不同模式二值图像按式(9)和(10)计算的重建误差SIE和RMSE。双模式重建的SIE为0.119,RMSE则为6.5%,双模式数据融合算法的成像精度较两种单模式算法有较大提高,对颗粒的位置、大小和形状信息呈现更精准。
|
|
表 1 重建结果的SIE和RMSE Table 1 SIE and RMSE of reconstructed results |
(1) 柱面式PVDF小型化传感器的发射/接收面宽度(2.8±0.1) mm对管径80 mm的实验管段,可得颗粒尺寸测量下限约3 mm。
(2) 对不同尺寸和位置的四个钢珠颗粒体系而言,透射模式UPT未能反映尺寸接近换能器发射宽度的颗粒;而反射式UPT重建大颗粒封闭性差,易丢失颗粒轮廓信息。
(3) 双模式融合图像重建结合了透射式和反射式重建算法优势,可去除整个颗粒系轮廓外部的噪影,获得更为清晰颗粒系形态,同时较好解决了小颗粒识别和大颗粒不封闭问题。实验中颗粒体系成像误差明显小于单模式成像。
| [1] | Nguyen T T, Kikura H, Murakawa H, et al. Measurement of bubbly two-phase flow in vertical pipe using multiwave ultrasonic pulsed dopller method and wire mesh tomography[J]. Energy Procedia, 2015, 71(7): 186-191. |
| [2] | CHEN Gong(陈珙), WANG Bao-liang(王保良), YANG Jiang(杨江), et al. Application of wavelets transform to the fuzzy identification of gas-liquid two-phase flow regimes(基于小波分析的气液两相流流型模糊辨识)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 1999, 13(4): 303-308. |
| [3] | Chang Y, Huang Z Y, Wang B L, et al. A new method for void fraction measurement of gas-liquid two-phase flow based on C~4D technique[J]. Journal of Engineering Thermophysics, 2014, 34(2): 294-297. |
| [4] | SHAO Xiao-yin(邵晓寅), HUANG Zhi-yao(黄志尧), JI Hai-feng(冀海峰), et al. Study on flow pattern identification of gas-oil two-phase flow based on electrical capacitance tomography and fuzzy pattern recognition(基于电容层析成像和模糊模式识别的油气两相流流型辨识新方法的研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2003, 17(6): 616-621. DOI:10.3321/j.issn:1003-9015.2003.06.003. |
| [5] | WANG Wei-wei(王微微), WANG Bao-liang(王保良), HUANG Zhi-yao(黄志尧), et al. Voidage measurement of oil-gas two-phase flow using electrical capacitance tomography technique(利用电容层析成像技术快速测量油气两相流空隙率的研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2006, 20(4): 515-519. DOI:10.3321/j.issn:1003-9015.2006.04.004. |
| [6] | QIN Yu-jian(秦玉建), JIN Hai-bo(靳海波), YANG Suo-he(杨索和). Local bubble parameters in a pressurized gas-liquid bubble column reactor measured by electrical resistance tomography(采用电阻层析成像技术测量气液加压鼓泡塔局部气泡参数)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2013, 27(3): 372-379. DOI:10.3969/j.issn.1003-9015.2013.03.002. |
| [7] | Rahiman M H F, Rahim R A, Rahim H A, et al. An investigation on chemical bubble column using ultrasonic tomography for imaging of gas profiles[J]. Sensors & Actuators B Chemical, 2014, 202(10): 46-52. |
| [8] | Nordin N, Idroas M, Zakaria Z A, et al. Hardware development of reflection mode ultrasonic tomography system for monitoring flaws on pipeline[J]. Jurnal Teknologi, 2015, 73(3): 13-18. |
| [9] | Xu L, Han Y, Xu L A, et al. Application of ultrasonic tomography to monitoring gas/liquid flow[J]. Chemical Engineering Science, 1997, 52(13): 2171-2183. DOI:10.1016/S0009-2509(97)00043-2. |
| [10] | Shin T H, Choi Y, Kim S, et al. Recent advances in magnetic nanoparticle-based multi-modal imaging[J]. Chemical Society Reviews, 2015, 44(14): 4501-4516. DOI:10.1039/C4CS00345D. |
| [11] | Hoyle B S, Jia X, Podd F J W, et al. Design and application of a multi-modal process tomography system[J]. Measurement Science & Technology, 2001, 12(8): 1157-1165. |
| [12] | Teniou S, Meribout M. A multimodal image reconstruction method using ultrasonic waves and electrical resistance tomography[J]. IEEE Transactions on Image Processing, 2015, 24(11): 3512-3521. DOI:10.1109/TIP.2015.2445575. |
| [13] | Schlaberg H I, Yang M, Hoyle B S. Ultrasound reflection tomography for industrial processes[J]. Ultrasonics, 1998, 36(1-5): 297-303. DOI:10.1016/S0041-624X(97)00053-X. |
| [14] | Yang L, Pan Q, Xu C, et al. Immersion ultrasonic reflection tomography by annular array system[C]//Nondestructive Evaluation/Testing: New Technology & Application. Washington: IEEE, 2013: 82-89. |
| [15] | TIAN Chang(田昌), SU Ming-xu(苏明旭), GU Jian-fei(顾建飞). Ultrasonic process tomography system of gas-solid two-phase flow measurement(气固两相流超声过程层析成像系统研究)[J]. Chinese Journal of Scientific Instrument(仪器仪表学报), 2016, 37(3): 586-592. DOI:10.3969/j.issn.0254-3087.2016.03.015. |
| [16] | Faramarzi M, Ibrahim S, Yunus M A M, et al. Image reconstruction methods for ultrasonic transmission mode tomography in bubbly flow regime[J]. Jurnal Teknologi, 2014, 20(4): 705-712. |
| [17] | Silva G T, Mitri F G. Difference-frequency generation in vibro-acoustography[J]. Physics in Medicine & Biology, 2011, 56(18): 5985-5993. |
| [18] | GU Jian-fei(顾建飞), SU Ming-xu(苏明旭), CAI Xiao-shu(蔡小舒). The COMSOL based sound filed simulation and image reconstruction of ultrasonic tomography(基于COMSOL的超声层析成像仿真及图像重建)[J]. Technical Acoustics(声学技术), 2016, 35(3): 231-234. |
| [19] | Langener S, Vogt M, Ermert H, et al. A real-time ultrasound process tomography system using a reflection-mode reconstruction technique[J]. Flow Measurement & Instrumentation, 2017, 53 Part A: 107-115. |
| [20] | Cardoso G, Saniie J. Ultrasonic data compression via parameter estimation[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2005, 52(2): 313-325. |
| [21] | Rahiman M H F, Rahim R A, Rahim H A, et al. Ultrasonic tomography image reconstruction algorithms[J]. International Journal of Innovative Computing Information & Control, 2012, 8(1): 527-538. |
| [22] | GU Jian-fei(顾建飞), SU Ming-xu(苏明旭), CAI Xiao-shu(蔡小舒). Development of a digital 8-channel ultrasonic process tomography system(数字式8通道超声过程层析成像系统研制)[J]. Journal of Engineering Thermophysics(工程热物理学报), 2016, 37(4): 785-789. |




