四次型状态方程计算若干物质的固-液-气三相物性
张任洁
1,
云志
2,
陈群
1

,
钱俊峰
1,
孙中华
1
1. 常州大学 石油化工学院, 江苏 常州 213164;
2. 南京工业大学, 江苏 南京 211816
收稿日期:2023-03-05;修订日期:2023-05-12。
作者简介:张任洁(1997-),女,甘肃兰州人,常州大学硕士生。
摘要:为考察四次型状态方程(CCOR-PT EOS)的性能,对苯酚、乙烷、正壬烷、丙酮、乙酸乙酯、二氧化碳、甲苯、正庚烷、乙炔、正己烷、辛烷11个物质的固-液-气三相压力、体积、温度(PVT)物性,使用CCOR-PT EOS进行计算,并与文献数据相比较。同时考察了物质的固有参数对计算结果的影响。结果表明,该方程能够较好地描述包括固体升华压力、固体密度等在内的三相PVT物性,计算结果对临界压缩因子ZC的敏感程度大于偏心因子ω。
关键词:状态方程 固体 三相 物性 四次型
Calculation of solid-liquid-vapor PVT properties of pure substances using a quartic CCOR-PT equation of state
ZHANG Renjie
1,
YUN Zhi
2,
CHEN Qun
1

,
QIAN Junfeng
1,
SUN Zhonghua
1
1. School of Petrochemical Engineering, Changzhou University, Changzhou 213164, China;
2. Nanjing Tech University, Nanjing 211816, China
Abstract: To evaluate the performance of a quartic CCOR-PT equation of state (CCOR-PT EOS), the solid-liquid-vapor PVT(pressure, volume, temperature) properties of 11 different compounds, including phenol, ethane, n-nonane, acetone, ethyl acetate, carbon dioxide, toluene, n-heptane, acetylene, n-hexane, and octane, were calculated using the CCOR-PT EOS. The calculated results were compared with literature data, and the effects of material intrinsic parameters on the calculation results were investigated. The results show that the equation could well describe the PVTproperties of three-phase, including the sublimation pressure and density of solids. The calculated results are more sensitive to the critical compression factor ZC than to eccentric factor ω.
Key words:
equation of state solids three-phase physical properties quartic type
1 前言
一般来说,传统的状态方程(EOS)是为流体设计的[1-3],通常用于计算液体、蒸气或超临界流体或者它们的混合物,但是难以用一个传统的状态方程来描述固-液-气三相的物性[4-6]。为了计算固体性质,通常需要单独的方程,甚至为了某种固体,有时需要构筑一个专用的表达式[7]。Yun等[8-10]给出了一个新的四次型状态方程(CCOR-PT EOS),该方程的体积函数形式是由CCOR状态方程的斥力项和PT状态方程的引力项组成[11-12],Yun等[8]构筑了新的温度函数,并对温度函数中的参数给出了70余种物质的具体数值,对非极性物质给出了有关参数的求取通式。该方程能够像常规的立方型状态方程一样使用求解公式得到解析解,其描述液相、气相流体的计算精度相当于常用的立方型状态方程,并且在比较低的对比温度区域里计算流体压力、体积、温度(PVT)性质的精度往往优于常用的立方型状态方程。CCOR-PT EOS的一个最重要的特点是它能够计算固体的PVT性质,Yun等[8]对这一特点做了初步阐述。但其计算的一些物质的温度范围尚不够宽,如对CO2等在低温固汽共存条件下的PVT尚缺少计算,有关计算结果对物质参数的敏感性也缺少考察。本研究对该方程应用于纯物质固-液-气三相相行为的计算进行进一步考察及验证,并且探讨纯物质固有参数对该方程计算结果的影响。
2 四次型状态方程(CCOR-PT EOS)简介
CCOR-PT EOS的体积形式如下[8]:
|
$ Z = \frac{{{V_{\text{m}}} + 0.77b}}{{{V_{\text{m}}} - 0.42b}} - \frac{{a{V_{\text{m}}}}}{{{V_{\text{m}}}({V_{\text{m}}} + b) + ({V_{\text{m}}} - b)c}} $
|
(1) |
如何求取式中各参数,文献[8]给出了具体的表达式。
在常规立方型EOS的3个根中,最大的体积根代表蒸气,最小的代表液体,中间4个根,Vm1、Vm 2、Vm 3和Vm 4,从大到小排列。Vm 1和Vm 3分别表示蒸气和液体的摩尔体积。Vm 2的大小与立方型EOS的中间根相似,也是没有物理意义的。${V_{\text{m}}}_4$是最小的一个根,而且总是负的。在计算中,固体的摩尔体积Vm, S用Vm 3和Vm 4的组合来表示,公式如下:
|
$ V_{\mathrm{m}, \mathrm{S}}=V_{\mathrm{m} 3}+d \times V_{\mathrm{m} 4} $
|
(2) |
|
$ d = 1.681{\text{ }}13\omega - 0.217{\text{ }}084 $
|
(3) |
3 三相PVT物性计算
根据相平衡基本原理:当两相平衡时,各相的逸度必须相等。在给定温度后,调整压力就可以通过状态方程计算出两相体积,将温度、压力和各相的体积数值代入逸度计算公式,就可以进行各相的逸度数值比较。这种压力调整、逸度数值比较的操作循环进行,直到两相的逸度数值相等为止,此时的压力、各相的体积数值也就是计算得到的最终结果。本研究分别对11个纯物质进行了计算,计算结果和相应的文献值见表 1~ 11,图 1~ 11为计算值与文献值的对比图。
表 1(a)
Table 1(a)

表 1(a) 苯酚在固体状态下的密度和升华压力
Table 1(a) Density and sublimation pressure of phenol at solid state
| T/K |
Solid density / (g·cm−3) |
|
Sublimation pressure / MPa |
| Calculated value |
Experiment value[13] |
Calculated value |
Calculated value[14] |
| 263.15 |
1.181 |
|
|
1.600×10−5 |
|
| 268.15 |
1.174 |
|
2.465×10−5 |
|
| 273.15 |
1.168 |
|
3.727×10−5 |
3.730×10−5 |
| 278.15 |
1.161 |
|
5.537×10−5 |
6.130×10−5 |
| 283.15 |
1.155 |
|
8.092×10−5 |
1.170×10−4 |
| 288.15 |
1.149 |
|
1.164×10−4 |
1.683×10−4 |
| 293.15 |
1.142 |
1.060 |
1.650×10−4 |
2.386×10−4 |
| 298.15 |
1.136 |
1.132 |
2.307×10−4 |
3.335×10−4 |
| 303.15 |
1.130 |
1.071 |
3.184×10−4 |
4.602×10−4 |
| 308.15 |
1.124 |
|
4.339×10−4 |
6.271×10−4 |
| 313.15 |
1.118 |
1.054 |
5.842×10−4 |
8.444×10−4 |
|
表 1(a) 苯酚在固体状态下的密度和升华压力
Table 1(a) Density and sublimation pressure of phenol at solid state |
表 1(b)
Table 1(b)

表 1(b) 苯酚在沸点以下的密度和蒸气压
Table 1(b) Density and vapour pressure of phenol below the boiling point
| T/K |
Liquid density / (g·cm−3) |
|
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Experiment value[13] |
Calculated value |
Calculated value[15] |
| 333.15 |
0.960 0 |
1.042 |
1.041 |
|
1.574×10−3 |
0.6578×10−3 |
| 343.15 |
0.955 7 |
1.033 |
1.032 |
2.555×10−3 |
1.180×10−3 |
| 353.15 |
0.944 9 |
1.024 |
|
4.013×10−3 |
2.050×10−3 |
| 363.15 |
0.934 3 |
1.015 |
|
6.114×10−3 |
3.400×10−3 |
| 373.15 |
0.923 8 |
1.006 |
|
9.063×10−3 |
5.470×10−3 |
| 383.15 |
0.913 5 |
0.996 4 |
|
1.310×10−2 |
8.530×10−3 |
| 393.15 |
0.903 1 |
0.987 0 |
|
1.851×10−2 |
1.292×10−2 |
| 403.15 |
0.892 9 |
0.977 6 |
|
2.560×10−2 |
1.905×10−2 |
| 413.15 |
0.882 8 |
0.968 0 |
|
3.474×10−2 |
2.744×10−2 |
| 423.15 |
0.872 8 |
0.958 2 |
|
4.632×10−2 |
3.864×10−2 |
| 443.15 |
0.861 5 |
0.938 3 |
|
7.754×10−2 |
7.218×10−2 |
| 453.15 |
0.851 0 |
0.928 1 |
|
1.001×10−1 |
9.606×10−2 |
|
表 1(b) 苯酚在沸点以下的密度和蒸气压
Table 1(b) Density and vapour pressure of phenol below the boiling point |
表 1(c)
Table 1(c)

表 1(c) 苯酚在沸点以上的密度和蒸气压
Table 1(c) Density and vapour pressure of phenol above the boiling point
| T/K |
Gas density / (g·cm-3) |
Liquid density / (g·cm-3) |
Vapour pressure / MPa |
| Calculated value |
Calculated value[16] |
| 463.15 |
0.006 10 |
0.832 9 |
0.126 1 |
0.126 2 |
| 473.15 |
0.007 20 |
0.822 9 |
0.156 9 |
0.162 9 |
| 483.15 |
0.008 60 |
0.812 9 |
0.193 1 |
0.207 6 |
| 493.15 |
0.009 70 |
0.802 7 |
0.235 3 |
|
| 503.15 |
0.011 90 |
0.792 5 |
0.284 2 |
|
| 513.15 |
0.013 90 |
0.782 1 |
0.340 3 |
|
| 523.15 |
0.016 20 |
0.771 8 |
0.404 3 |
|
| 533.15 |
0.018 90 |
0.760 0 |
0.476 8 |
|
| 543.15 |
0.020 90 |
0.752 0 |
0.558 6 |
|
| 553.15 |
0.024 20 |
0.748 0 |
0.659 9 |
|
| 563.15 |
0.028 50 |
0.736 6 |
0.782 5 |
|
| 573.15 |
0.032 30 |
0.724 4 |
0.891 3 |
|
| Note: The values calculated in this paper are not explained in the table, the same below. |
|
表 1(c) 苯酚在沸点以上的密度和蒸气压
Table 1(c) Density and vapour pressure of phenol above the boiling point |
表 2(a)
Table 2(a)

表 2(a) 乙烷在固体状态下的密度和升华压力
Table 2(a) Density and sublimation pressure of ethane at solid state
| T/K |
Solid density / (g·cm−3) |
Sublimation pressure / MPa |
| 39.85 |
0.797 2 |
1.240×10−21 |
| 49.85 |
0.764 2 |
4.700×10−16 |
| 59.85 |
0.734 7 |
1.864×10−12 |
| 69.85 |
0.708 2 |
5.810×10−12 |
| 79.85 |
0.684 2 |
3.820×10−8 |
|
表 2(a) 乙烷在固体状态下的密度和升华压力
Table 2(a) Density and sublimation pressure of ethane at solid state |
表 2(b)
Table 2(b)

表 2(b) 乙烷在沸点以下的密度和蒸气压
Table 2(b) Density and vapour pressure of ethane below the boiling point
| T/K |
Liquid density / (g·cm−3) |
|
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 89.85 |
0.669 7 |
0.651 2 |
|
9.040×10−7 |
9.870×10−7 |
| 99.85 |
0.649 7 |
0.641 0 |
1.064×10−5 |
1.070×10−5 |
| 109.85 |
0.631 2 |
0.630 5 |
7.596×10−5 |
7.236×10−5 |
| 119.85 |
0.614 0 |
0.619 9 |
3.748×10−4 |
3.448×10−4 |
| 129.85 |
0.597 8 |
0.609 0 |
1.399×10−3 |
1.260×10−3 |
| 139.85 |
0.582 5 |
0.597 9 |
4.208×10−3 |
3.751×10−3 |
| 149.85 |
0.568 0 |
0.586 5 |
1.069×10−2 |
9.499×10−3 |
| 159.85 |
0.554 2 |
0.574 8 |
2.373×10−2 |
2.114×10−2 |
| 169.85 |
0.540 8 |
0.562 8 |
4.728×10−2 |
4.236×10−2 |
| 173.15 |
0.536 5 |
0.558 8 |
5.816×10−2 |
5.224×10−2 |
| 179.85 |
0.527 9 |
0.550 4 |
8.621×10−2 |
7.791×10−2 |
|
表 2(b) 乙烷在沸点以下的密度和蒸气压
Table 2(b) Density and vapour pressure of ethane below the boiling point |
表 2(c)
Table 2(c)

表 2(c) 乙烷在沸点以上的密度和蒸气压
Table 2(c) Density and vapour pressure of ethane above the boiling point
| T/K |
Gas density / (g·cm−3) |
|
Vapour pressure / MPa |
|
Liquid density / (g·cm−3) |
| Calculated value |
Literature data[18] |
Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 199.85 |
0.004 40 |
0.004 50 |
|
0.233 6 |
0.215 7 |
|
0.502 7 |
0.524 3 |
| 209.85 |
0.006 60 |
0.006 70 |
0.354 9 |
0.331 8 |
0.490 2 |
0.510 4 |
| 219.85 |
0.009 40 |
0.009 60 |
0.517 0 |
0.489 3 |
0.477 5 |
0.495 9 |
| 229.85 |
0.013 00 |
0.013 50 |
0.727 0 |
0.696 7 |
0.464 6 |
0.480 6 |
| 239.85 |
0.017 60 |
0.017 90 |
0.992 3 |
0.962 3 |
0.450 9 |
0.464 3 |
| 249.85 |
0.023 40 |
0.024 30 |
1.321 |
1.295 |
0.436 4 |
0.446 8 |
| 259.85 |
0.031 00 |
0.032 50 |
1.720 |
1.705 |
0.420 2 |
0.427 7 |
| 269.85 |
0.041 00 |
0.042 20 |
2.202 |
2.203 |
0.401 7 |
0.406 4 |
|
表 2(c) 乙烷在沸点以上的密度和蒸气压
Table 2(c) Density and vapour pressure of ethane above the boiling point |
表 3(a)
Table 3(a)

表 3(a) 正壬烷在固体状态下的密度和升华压力
Table 3(a) Density and sublimation pressure of n-nonane at solid state
| T/K |
Solid density / (g·cm−3) |
Sublimation pressure / MPa |
| Calculated value |
Calculated value[16] |
| 143.15 |
0.914 3 |
|
1.217×10−10 |
| 153.15 |
0.903 5 |
|
1.247×10−9 |
| 163.15 |
0.892 8 |
|
9.320×10−9 |
| 173.15 |
0.882 2 |
|
5.387×10−8 |
| 183.15 |
0.871 8 |
|
2.514×10−7 |
| 193.15 |
0.861 4 |
|
9.808×10−7 |
| 203.15 |
0.851 2 |
|
3.290×10−6 |
| 213.15 |
0.841 0 |
|
9.704×10−6 |
| 223.15 |
0.831 0 |
0.772 5 |
2.563×10−5 |
|
表 3(a) 正壬烷在固体状态下的密度和升华压力
Table 3(a) Density and sublimation pressure of n-nonane at solid state |
表 3(b)
Table 3(b)

表 3(b) 正壬烷在沸点以下的密度和蒸气压
Table 3(b) Density and vapour pressure of n-nonane below the boiling point
| T/K |
Liquid density / (g·cm−3) |
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 243.15 |
0.737 2 |
0.758 2 |
1.359×10−4 |
6.723×10−6 |
| 263.15 |
0.719 5 |
0.743 5 |
5.386×10−4 |
4.424×10−5 |
| 283.15 |
0.702 6 |
0.728 5 |
1.703×10−3 |
2.118×10−4 |
| 303.15 |
0.686 3 |
0.713 1 |
4.510×10−3 |
7.904×10−4 |
| 323.15 |
0.670 6 |
0.697 2 |
1.040×10−2 |
2.420×10−3 |
| 343.15 |
0.655 2 |
0.680 9 |
2.130×10−2 |
6.320×10−3 |
| 363.15 |
0.640 1 |
0.664 1 |
3.980×10−2 |
1.450×10−2 |
| 383.15 |
0.625 1 |
0.646 6 |
6.910×10−2 |
2.993×10−2 |
| 403.15 |
0.610 0 |
0.628 4 |
1.126×10−1 |
5.661×10−2 |
| 423.15 |
0.594 6 |
0.609 4 |
1.742×10−1 |
9.958×10−2 |
|
表 3(b) 正壬烷在沸点以下的密度和蒸气压
Table 3(b) Density and vapour pressure of n-nonane below the boiling point |
表 3(c)
Table 3(c)

表 3(c) 正壬烷在沸点以上的密度和蒸气压
Table 3(c) Density and vapour pressure of n-nonane above the boiling point
| T/K |
Gas density / (g·cm−3) |
Vapour pressure / MPa |
|
Liquid density / (g·cm−3) |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 433.15 |
0.008 20 |
0.213 2 |
0.129 0 |
|
0.586 8 |
0.599 6 |
| 443.15 |
0.010 00 |
0.258 4 |
0.164 9 |
0.578 7 |
0.589 4 |
| 453.15 |
0.011 90 |
0.310 3 |
0.208 1 |
0.570 4 |
0.579 0 |
| 463.15 |
0.014 10 |
0.369 6 |
0.259 5 |
0.561 9 |
0.568 2 |
| 473.15 |
0.016 70 |
0.436 9 |
0.320 3 |
0.553 0 |
0.557 0 |
| 483.15 |
0.019 60 |
0.513 1 |
0.391 5 |
0.543 7 |
0.545 4 |
| 493.15 |
0.023 00 |
0.598 7 |
0.474 3 |
0.533 8 |
0.533 2 |
| 503.15 |
0.027 00 |
0.694 6 |
0.569 9 |
0.523 2 |
0.520 5 |
| 513.15 |
0.031 60 |
0.801 9 |
0.679 6 |
0.511 8 |
0.507 1 |
| 523.15 |
0.037 00 |
0.921 4 |
0.804 9 |
0.499 4 |
0.492 9 |
|
表 3(c) 正壬烷在沸点以上的密度和蒸气压
Table 3(c) Density and vapour pressure of n-nonane above the boiling point |
表 4(a)
Table 4(a)

表 4(a) 丙酮在固体状态下的密度和升华压力
Table 4(a) Density and sublimation pressure of acetone at solid state
| T/K |
Solid density / (g·cm−3) |
|
Sublimation pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 103.15 |
1.047 |
|
|
5.050×10−15 |
|
| 113.15 |
1.032 |
|
4.190×10−13 |
|
| 123.15 |
1.017 |
|
1.580×10−11 |
|
| 133.15 |
1.002 |
|
3.290×10−10 |
|
| 143.15 |
0.987 0 |
|
4.260×10−9 |
|
| 153.15 |
0.973 0 |
|
3.810×10−8 |
|
| 163.15 |
0.959 0 |
|
2.510×10−7 |
|
| 173.15 |
0.945 0 |
|
1.300×10−6 |
|
| 183.15 |
0.931 7 |
0.906 3 |
5.460×10−6 |
5.240×10−6 |
|
表 4(a) 丙酮在固体状态下的密度和升华压力
Table 4(a) Density and sublimation pressure of acetone at solid state |
表 4(b)
Table 4(b)

表 4(b) 丙酮在沸点以下的密度和蒸气压
Table 4(b) Density and vapour pressure of acetone below boiling point
| T/K |
Liquid density / (g·cm−3) |
|
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 193.15 |
0.876 6 |
0.896 6 |
|
1.940×10−5 |
1.790×10−5 |
| 213.15 |
0.891 8 |
0.876 9 |
1.620×10−4 |
1.420×10−4 |
| 233.15 |
0.826 4 |
0.856 7 |
8.870×10−4 |
7.563×10−4 |
| 253.15 |
0.802 7 |
0.835 9 |
3.540×10−3 |
2.988×10−3 |
| 273.15 |
0.779 6 |
0.814 4 |
1.110×10−2 |
9.391×10−3 |
| 293.15 |
0.757 0 |
0.792 3 |
2.900×10−2 |
2.471×10−2 |
| 313.15 |
0.734 5 |
0.769 2 |
6.520×10−2 |
5.650×10−2 |
| 323.15 |
0.723 2 |
0.757 4 |
9.340×10−2 |
8.178×10−2 |
|
表 4(b) 丙酮在沸点以下的密度和蒸气压
Table 4(b) Density and vapour pressure of acetone below boiling point |
表 4(c)
Table 4(c)

表 4(c) 丙酮在沸点以上的密度和蒸气压
Table 4(c) Density and vapour pressure of acetone above the boiling point
| T/K |
Gas density / (g·cm−3) |
|
Vapour pressure / MPa |
|
Liquid density / (g·cm−3) |
| Calculated value |
Literature data[18] |
Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 333.15 |
0.002 80 |
0.002 70 |
|
0.130 6 |
0.115 4 |
|
0.711 8 |
0.745 2 |
| 343.15 |
0.003 80 |
0.003 50 |
0.178 3 |
0.159 3 |
0.700 3 |
0.732 8 |
| 353.15 |
0.005 00 |
0.004 40 |
0.238 4 |
0.215 3 |
0.688 7 |
0.720 0 |
| 363.15 |
0.006 40 |
0.006 60 |
0.313 0 |
0.285 8 |
0.676 8 |
0.706 9 |
| 373.15 |
0.008 20 |
0.007 80 |
0.404 0 |
0.372 9 |
0.664 6 |
0.693 4 |
| 383.15 |
0.010 30 |
0.009 60 |
0.513 6 |
0.479 3 |
0.652 0 |
0.679 4 |
| 393.15 |
0.012 90 |
0.013 60 |
0.644 1 |
0.607 6 |
0.639 0 |
0.664 9 |
| 403.15 |
0.015 90 |
0.016 00 |
0.798 0 |
0.760 6 |
0.625 4 |
0.649 8 |
| 413.15 |
0.019 50 |
0.019 10 |
0.977 6 |
0.941 2 |
0.611 0 |
0.634 1 |
|
表 4(c) 丙酮在沸点以上的密度和蒸气压
Table 4(c) Density and vapour pressure of acetone above the boiling point |
表 5(a)
Table 5(a)

表 5(a) 乙酸乙酯在固体状态下的密度和升华压力
Table 5(a) Density and sublimation pressure of ethyl acetate at solid state
| T/K |
Solid density / (g·cm−3) |
|
Sublimation pressure/MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 113.15 |
1.068 |
|
|
4.487×10−16 |
|
| 123.15 |
1.054 |
|
4.227×10−14 |
|
| 133.15 |
1.040 |
|
1.858×10−12 |
|
| 143.15 |
1.027 |
|
4.503×10−11 |
|
| 153.15 |
1.012 |
|
6.806×10−10 |
|
| 163.15 |
0.999 6 |
|
7.030×10−9 |
|
| 173.15 |
0.986 2 |
|
5.321×10−8 |
|
| 183.15 |
0.973 0 |
|
3.115×10−7 |
|
| 193.15 |
0.959 9 |
0.883 0 |
1.472×10−6 |
2.325×10−6 |
|
表 5(a) 乙酸乙酯在固体状态下的密度和升华压力
Table 5(a) Density and sublimation pressure of ethyl acetate at solid state |
表 5(b)
Table 5(b)

表 5(b) 乙酸乙酯在沸点以下的密度和蒸气压
Table 5(b) Density and vapour pressure of ethyl acetate below the boiling point
| T/K |
Liquid density / (g·cm−3) |
|
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 203.15 |
0.880 6 |
0.874 1 |
|
5.804×10−6 |
8.229×10−6 |
| 223.15 |
0.855 2 |
0.855 9 |
5.826×10−5 |
7.040×10−5 |
| 243.15 |
0.830 9 |
0.837 3 |
3.709×10−4 |
4.038×10−4 |
| 263.15 |
0.807 4 |
0.818 1 |
1.675×10−3 |
1.708×10−3 |
| 283.15 |
0.784 6 |
0.798 3 |
5.812×10−3 |
5.702×10−3 |
| 303.15 |
0.762 2 |
0.777 8 |
1.642×10−2 |
1.578×10−2 |
| 323.15 |
0.740 1 |
0.756 5 |
3.944×10−2 |
3.761×10−2 |
| 343.15 |
0.718 1 |
0.734 2 |
8.328×10−2 |
7.940×10−2 |
|
表 5(b) 乙酸乙酯在沸点以下的密度和蒸气压
Table 5(b) Density and vapour pressure of ethyl acetate below the boiling point |
表 5(c)
Table 5(c)

表 5(c) 乙酸乙酯在沸点以上的密度和蒸气压
Table 5(c) Density and vapour pressure of ethyl acetate above the boiling point
| T/K |
Gas density / (g·cm−3) |
Vapour pressure / MPa |
|
Liquid density / (g·cm−3) |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 353.15 |
0.003 20 |
0.116 3 |
0.111 0 |
|
0.707 0 |
0.722 7 |
| 363.15 |
0.004 20 |
0.158 6 |
0.151 8 |
0.695 7 |
0.710 9 |
| 373.15 |
0.005 60 |
0.211 9 |
0.203 5 |
0.684 3 |
0.698 7 |
| 383.15 |
0.007 20 |
0.277 9 |
0.267 7 |
0.672 7 |
0.686 1 |
| 393.15 |
0.009 20 |
0.358 3 |
0.346 4 |
0.660 8 |
0.673 1 |
| 403.15 |
0.011 60 |
0.455 0 |
0.441 5 |
0.648 5 |
0.659 7 |
| 413.15 |
0.014 50 |
0.570 0 |
0.555 2 |
0.635 7 |
0.645 7 |
| 423.15 |
0.018 00 |
0.705 2 |
0.689 5 |
0.622 3 |
0.631 1 |
| 433.15 |
0.022 10 |
0.862 9 |
0.846 8 |
0.608 1 |
0.615 7 |
|
表 5(c) 乙酸乙酯在沸点以上的密度和蒸气压
Table 5(c) Density and vapour pressure of ethyl acetate above the boiling point |
表 6(a)
Table 6(a)

表 6(a) 二氧化碳在固体状态下的密度和升华压力
Table 6(a) Density and sublimation pressure of carbon dioxide at solid state
| T/K |
Solid density / (g·cm-3) |
Sublimation pressure / MPa |
| Calculated value |
Calculated value[19] |
| 103.15 |
1.646 |
5.890×10-7 |
6.498×10-8 |
| 113.15 |
1.601 |
8.210×10-6 |
9.554×10-7 |
| 123.15 |
1.558 |
2.750×10-5 |
9.078×10-6 |
| 133.15 |
1.517 |
3.930×10-4 |
6.150×10-5 |
| 143.15 |
1.477 |
1.660×10-3 |
3.190×10-4 |
| 153.15 |
1.437 |
5.580×10-3 |
1.334×10-3 |
| 163.15 |
1.399 |
1.550×10-2 |
4.560×10-3 |
| 173.15 |
1.361 |
3.710×10-2 |
1.379×10-2 |
| 183.15 |
1.323 |
7.860×10-2 |
3.686×10-2 |
| 193.15 |
1.286 |
1.506×10-1 |
8.880×10-2 |
| 203.15 |
1.248 |
2.657×10-1 |
1.961×10-1 |
| 213.15 |
1.210 |
4.380×10-1 |
4.012×10-1 |
|
表 6(a) 二氧化碳在固体状态下的密度和升华压力
Table 6(a) Density and sublimation pressure of carbon dioxide at solid state |
表 6(b)
Table 6(b)

表 6(b) 二氧化碳在气液共存状态下的密度和蒸气压
Table 6(b) Density and vapour pressure of carbon dioxide in the vapour-liquid coexistence state
| T/K |
Gas density / (g·cm−3) |
|
Vapour pressure / MPa |
|
Liquid density /(g·cm−3) |
| Calculated value |
Literature data[20] |
Calculated value[21] |
Calculated value[15] |
Calculated value[21] |
Calculated value[15] |
Experiment value[22] |
| 223.15 |
0.017 5 |
0.017 0 |
|
0.682 2 |
0.678 3 |
|
1.141 |
1.156 |
|
| 233.15 |
0.025 8 |
0.025 0 |
1.013 |
0.993 8 |
1.104 |
1.117 |
|
| 243.15 |
0.036 7 |
0.037 0 |
1.445 |
1.411 |
1.066 |
1.076 |
1.076 |
| 253.15 |
0.051 1 |
0.052 0 |
1.993 |
1.949 |
1.025 |
1.031 |
1.032 |
| 263.15 |
0.070 2 |
0.071 0 |
2.672 |
2.626 |
0.979 0 |
0.981 8 |
0.982 0 |
| 273.15 |
0.096 0 |
0.097 0 |
3.499 |
3.463 |
0.926 3 |
0.926 2 |
0.927 6 |
| 283.15 |
0.132 9 |
0.134 0 |
4.494 |
4.477 |
0.861 1 |
0.860 4 |
0.863 7 |
| 293.15 |
0.192 7 |
0.193 0 |
5.693 |
5.688 |
0.770 1 |
0.774 5 |
0.774 2 |
| 303.15 |
0.356 5 |
0.336 0 |
7.171 |
7.114 |
0.584 2 |
0.601 7 |
|
|
表 6(b) 二氧化碳在气液共存状态下的密度和蒸气压
Table 6(b) Density and vapour pressure of carbon dioxide in the vapour-liquid coexistence state |
表 7(a)
Table 7(a)

表 7(a) 甲苯在固体状态下的密度和升华压力
Table 7(a) Density and sublimation pressure of toluene at solid state
| T/K |
Solid density / (g·cm−3) |
|
Sublimation pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 103.15 |
1.096 |
|
|
1.530×10−17 |
|
| 113.15 |
1.079 |
|
2.140×10−17 |
|
| 123.15 |
1.062 |
|
1.250×10−13 |
|
| 133.15 |
1.045 |
|
3.770×10−12 |
|
| 143.15 |
1.029 |
|
6.740×10−11 |
|
| 153.15 |
1.014 |
|
7.950×10−10 |
|
| 163.15 |
0.999 0 |
|
6.710×10−9 |
|
| 173.15 |
0.984 5 |
0.970 3 |
4.300×10−8 |
1.986×10−8 |
| 183.15 |
0.970 4 |
0.962 3 |
2.200×10−7 |
1.068×10−7 |
|
表 7(a) 甲苯在固体状态下的密度和升华压力
Table 7(a) Density and sublimation pressure of toluene at solid state |
表 7(b)
Table 7(b)

表 7(b) 甲苯在沸点以下的密度和蒸气压
Table 7(b) Density and vapour pressure of toluene below the boiling point
| T/K |
Liquid density / (g·cm−3) |
|
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 193.15 |
0.910 3 |
0.954 2 |
|
9.290×10−7 |
4.726×10−7 |
| 223.15 |
0.871 0 |
0.929 4 |
2.930×10−5 |
1.678×10−5 |
| 253.15 |
0.835 0 |
0.903 9 |
3.640×10−4 |
2.300×10−4 |
| 283.15 |
0.801 7 |
0.877 5 |
2.450×10−3 |
1.676×10−3 |
| 313.15 |
0.770 3 |
0.850 1 |
1.070×10−2 |
7.900×10−3 |
| 343.15 |
0.740 4 |
0.821 4 |
3.480×10−2 |
2.710×10−2 |
| 383.15 |
0.701 4 |
0.780 9 |
1.189×10−1 |
9.940×10−2 |
|
表 7(b) 甲苯在沸点以下的密度和蒸气压
Table 7(b) Density and vapour pressure of toluene below the boiling point |
表 7(c)
Table 7(c)

表 7(c) 甲苯在沸点以上的密度和蒸气压
Table 7(c) Density and vapour pressure of toluene above the boiling point
| T/K |
Gas density / (g·cm−3) |
|
Vapour pressure / MPa |
|
Liquid density / (g·cm−3) |
| Calculated value |
Literature data[18] |
Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 393.15 |
0.004 50 |
0.004 10 |
|
0.154 5 |
0.131 1 |
|
0.691 7 |
0.770 2 |
| 403.15 |
0.005 70 |
0.005 20 |
0.197 7 |
0.170 3 |
0.682 0 |
0.759 4 |
| 413.15 |
0.007 10 |
0.006 40 |
0.249 5 |
0.218 0 |
0.672 2 |
0.748 3 |
| 423.15 |
0.008 70 |
0.008 00 |
0.310 9 |
0.275 4 |
0.662 2 |
0.736 9 |
| 433.15 |
0.010 70 |
0.009 60 |
0.383 0 |
0.343 7 |
0.652 1 |
0.725 2 |
| 443.15 |
0.012 90 |
0.011 50 |
0.467 0 |
0.424 1 |
0.641 8 |
0.713 1 |
| 453.15 |
0.015 40 |
0.014 00 |
0.563 8 |
0.518 1 |
0.631 3 |
0.700 7 |
|
表 7(c) 甲苯在沸点以上的密度和蒸气压
Table 7(c) Density and vapour pressure of toluene above the boiling point |
表 8(a)
Table 8(a)

表 8(a) 正庚烷在固体状态下的密度和升华压力
Table 8(a) Density and sublimation pressure of n-heptane at solid state
| T/K |
Solid density / (g·cm−3) |
Sublimation pressure/MPa |
| Calculated value |
Calculated value[15] |
| 123.15 |
0.922 8 |
7.310×10−14 |
|
| 133.15 |
0.910 3 |
2.460×10−12 |
|
| 143.15 |
0.898 0 |
4.810×10−11 |
|
| 153.15 |
0.888 0 |
6.130×10−10 |
|
| 163.15 |
0.874 1 |
5.520×10−9 |
|
| 173.15 |
0.862 4 |
3.740×10−8 |
|
| 183.15 |
0.850 8 |
2.000×10−7 |
2.002×10−7 |
|
表 8(a) 正庚烷在固体状态下的密度和升华压力
Table 8(a) Density and sublimation pressure of n-heptane at solid state |
表 8(b)
Table 8(b)

表 8(b) 正庚烷在沸点以下的密度和蒸气压
Table 8(b) Density and vapour pressure of n-heptane below the boiling point
| T/K |
Liquid density / (g·cm−3) |
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 203.15 |
0.770 0 |
0.755 0 |
3.980×10−6 |
3.268×10−6 |
| 233.15 |
0.737 6 |
0.732 4 |
9.220×10−5 |
7.741×10−5 |
| 263.15 |
0.707 2 |
0.708 9 |
9.270×10−4 |
7.975×10−4 |
| 293.15 |
0.678 4 |
0.684 4 |
5.330×10−3 |
4.703×10−3 |
| 323.15 |
0.650 5 |
0.658 6 |
2.070×10−2 |
1.881×10−2 |
| 353.15 |
0.622 8 |
0.631 2 |
6.120×10−2 |
5.699×10−2 |
|
表 8(b) 正庚烷在沸点以下的密度和蒸气压
Table 8(b) Density and vapour pressure of n-heptane below the boiling point |
表 8(c)
Table 8(c)

表 8(c) 正庚烷在沸点以上的密度和蒸气压
Table 8(c) Density and vapour pressure of n-heptane above the boiling point
| T/K |
Gas density / (g·cm−3) |
|
Vapour pressure/MPa |
|
Liquid density / (g·cm−3) |
| Calculated value |
Literature data[18] |
Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 373.15 |
0.003 80 |
0.004 00 |
|
0.112 1 |
0.106 2 |
|
0.604 0 |
0.611 9 |
| 383.15 |
0.004 90 |
0.004 90 |
0.147 5 |
0.140 9 |
0.594 5 |
0.601 8 |
| 393.15 |
0.007 30 |
0.006 20 |
0.191 0 |
0.183 8 |
0.584 7 |
0.591 4 |
| 403.15 |
0.009 60 |
0.007 50 |
0.243 7 |
0.236 1 |
0.575 1 |
0.580 8 |
| 413.15 |
0.013 00 |
0.009 00 |
0.306 8 |
0.299 2 |
0.565 2 |
0.569 7 |
|
表 8(c) 正庚烷在沸点以上的密度和蒸气压
Table 8(c) Density and vapour pressure of n-heptane above the boiling point |
表 9(a)
Table 9(a)

表 9(a) 乙炔在固体状态下的密度和升华压力
Table 9(a) Density and sublimation pressure of acetylene at solid state
| T/K |
Solid density / (g·cm−3) |
Sublimation pressure / MPa |
| Calculated value |
Calculated value[15] |
| 123.15 |
0.763 8 |
1.560×10−4 |
|
| 133.15 |
0.746 3 |
6.770×10−4 |
|
| 143.15 |
0.729 6 |
2.310×10−3 |
1.200×10−3 |
| 153.15 |
0.713 5 |
6.560×10−3 |
4.000×10−3 |
| 163.15 |
0.698 0 |
0.016 0 |
0.011 3 |
| 173.15 |
0.682 9 |
0.034 6 |
0.028 3 |
| 183.15 |
0.668 0 |
0.067 8 |
0.064 3 |
| 193.15 |
0.653 3 |
0.122 5 |
0.134 8 |
|
表 9(a) 乙炔在固体状态下的密度和升华压力
Table 9(a) Density and sublimation pressure of acetylene at solid state |
表 9(b)
Table 9(b)

表 9(b) 乙炔在沸点以下的密度和蒸气压
Table 9(b) Density and vapour pressure of acetylene below the boiling point
| T/K |
Liquid density / (g·cm−3) |
|
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 203.15 |
0.628 9 |
0.600 5 |
|
0.206 7 |
0.222 1 |
| 213.15 |
0.615 1 |
0.584 5 |
0.329 8 |
0.352 3 |
| 223.15 |
0.601 1 |
0.567 8 |
0.501 9 |
0.534 2 |
| 233.15 |
0.586 6 |
0.550 2 |
0.734 1 |
0.779 3 |
| 243.15 |
0.571 3 |
0.531 5 |
1.038 4 |
1.099 8 |
|
表 9(b) 乙炔在沸点以下的密度和蒸气压
Table 9(b) Density and vapour pressure of acetylene below the boiling point |
表 9(c)
Table 9(c)

表 9(c) 乙炔在沸点以上的密度和蒸气压
Table 9(c) Density and vapour pressure of acetylene above the boiling point
| T/K |
Gas density / (g·cm−3) |
|
Vapour pressure / MPa |
|
Liquid density / (g·cm−3) |
| Calculated value |
Literature data[20] |
Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 253.15 |
0.021 2 |
0.023 8 |
|
1.428 |
1.509 |
|
0.554 6 |
0.511 3 |
| 263.15 |
0.028 90 |
0.030 4 |
1.919 |
2.020 |
0.535 8 |
0.489 3 |
| 273.15 |
0.039 4 |
0.041 6 |
2.529 |
2.650 |
0.513 7 |
0.464 6 |
| 283.15 |
0.054 4 |
0.056 9 |
3.285 |
3.416 |
0.485 7 |
0.436 0 |
| 293.15 |
0.077 9 |
0.078 4 |
4.222 |
4.340 |
0.446 3 |
0.400 4 |
| 303.15 |
0.126 3 |
0.130 0 |
5.412 |
5.451 |
0.376 3 |
0.346 3 |
|
表 9(c) 乙炔在沸点以上的密度和蒸气压
Table 9(c) Density and vapour pressure of acetylene above the boiling point |
表 10(a)
Table 10(a)

表 10(a) 正己烷在固体状态下的密度和升华压力
Table 10(a) Density and sublimation pressure of n-hexane at solid state
| T/K |
Solid density / (g·cm−3) |
|
Sublimation pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 110 |
0.926 3 |
|
|
1.850×10−15 |
|
| 120 |
0.912 4 |
|
1.470×10−13 |
|
| 130 |
0.898 8 |
|
5.550×10−12 |
|
| 140 |
0.885 4 |
|
1.17×10−10 |
|
| 150 |
0.872 4 |
|
1.570×10−9 |
|
| 160 |
0.859 5 |
|
1.460×10−8 |
|
| 170 |
0.846 9 |
|
1.000×10−7 |
|
| 177.87 |
0.837 1 |
0.753 8 |
3.840×10−7 |
1.375×10−7 |
|
表 10(a) 正己烷在固体状态下的密度和升华压力
Table 10(a) Density and sublimation pressure of n-hexane at solid state |
表 10(b)
Table 10(b)

表 10(b) 正己烷在沸点以下的密度和蒸气压
Table 10(b) Density and vapour pressure of n-hexane below the boiling point
| T/K |
Liquid density / (g·cm−3) |
|
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 200 |
0.764 0 |
0.737 1 |
|
8.730×10−6 |
2.926×10−6 |
| 230 |
0.729 6 |
0.713 6 |
1.980×10−4 |
5.601×10−5 |
| 260 |
0.697 3 |
0.689 1 |
1.930×10−3 |
4.632×10−4 |
| 290 |
0.666 3 |
0.663 3 |
1.060×10−2 |
2.264×10−3 |
| 310 |
0.646 1 |
0.645 2 |
2.660×10−2 |
5.325×10−3 |
| 341.9 |
0.613 9 |
0.614 6 |
8.720×10−2 |
1.636×10−2 |
|
表 10(b) 正己烷在沸点以下的密度和蒸气压
Table 10(b) Density and vapour pressure of n-hexane below the boiling point |
表 10(c)
Table 10(c)

表 10(c) 正己烷在沸点以上的密度和蒸气压
Table 10(c) Density and vapour pressure of n-hexane above the boiling point
| T/K |
Gas density /(g·cm−3) |
|
Vapour pressure / MPa |
|
Liquid density / (g·cm−3) |
| Calculated value |
Literature data[18] |
Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 350 |
0.003 50 |
0.004 10 |
|
0.113 2 |
0.129 6 |
|
0.605 6 |
0.606 4 |
| 360 |
0.004 60 |
0.005 00 |
0.153 0 |
0.172 4 |
0.595 2 |
0.596 1 |
| 370 |
0.006 10 |
0.007 30 |
0.202 8 |
0.225 2 |
0.584 6 |
0.585 4 |
| 380 |
0.007 80 |
0.008 90 |
0.264 2 |
0.289 7 |
0.573 7 |
0.574 3 |
| 390 |
0.009 90 |
0.010 50 |
0.338 8 |
0.367 3 |
0.562 5 |
0.562 8 |
| 400 |
0.012 50 |
0.014 70 |
0.428 3 |
0.459 8 |
0.550 8 |
0.550 8 |
|
表 10(c) 正己烷在沸点以上的密度和蒸气压
Table 10(c) Density and vapour pressure of n-hexane above the boiling point |
表 11(a)
Table 11(a)

表 11(a) 辛烷在固体状态下的密度和升华压力
Table 11(a) Density and sublimation pressure of octane at solid state
| T/K |
Solid density / (g·cm−3) |
Sublimation pressure / MPa |
| 143.15 |
0.926 3 |
1.040×10−12 |
| 153.15 |
0.915 4 |
1.960×10−11 |
| 163.15 |
0.904 6 |
2.460×10−10 |
| 173.15 |
0.893 9 |
2.220×10−9 |
| 183.15 |
0.883 2 |
1.520×10−8 |
| 193.15 |
0.872 6 |
8.320×10−8 |
| 203.15 |
0.862 0 |
3.750×10−7 |
| 213.15 |
0.851 5 |
1.430×10−6 |
|
表 11(a) 辛烷在固体状态下的密度和升华压力
Table 11(a) Density and sublimation pressure of octane at solid state |
表 11(b)
Table 11(b)

表 11(b) 辛烷在沸点以下的密度和蒸气压
Table 11(b) Density and vapor pressure of octane below the boiling point
| T/K |
Liquid density / (g·cm−3) |
|
Vapour pressure / MPa |
| Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 223.15 |
0.773 8 |
0.760 9 |
|
4.760×10−6 |
8.983×10−6 |
| 253.15 |
0.743 5 |
0.738 3 |
8.970×10−5 |
1.681×10−4 |
| 283.15 |
0.714 8 |
0.714 8 |
8.100×10−4 |
1.428×10−3 |
| 313.15 |
0.687 1 |
0.690 3 |
4.400×10−3 |
7.299×10−3 |
| 343.15 |
0.660 2 |
0.664 6 |
1.670×10−2 |
2.638×10−2 |
| 373.15 |
0.633 2 |
0.637 5 |
4.870×10−2 |
7.453×10−2 |
| 398.15 |
0.610 3 |
0.613 5 |
1.022×10−1 |
1.538×10−1 |
|
表 11(b) 辛烷在沸点以下的密度和蒸气压
Table 11(b) Density and vapor pressure of octane below the boiling point |
表 11(c)
Table 11(c)

表 11(c) 辛烷在沸点以上的密度和蒸气压
Table 11(c) Density and vapor pressure of octane above the boiling point
| T/K |
Gas density / (g·cm−3) |
|
Vapour pressure / MPa |
|
Liquid density / (g·cm−3) |
| Calculated value |
Literature data[18] |
Calculated value |
Calculated value[15] |
Calculated value |
Calculated value[15] |
| 408.15 |
0.004 70 |
0.004 70 |
|
0.133 3 |
0.130 4 |
|
0.600 9 |
0.603 5 |
| 418.15 |
0.006 00 |
0.005 70 |
0.171 3 |
0.168 4 |
0.591 3 |
0.593 1 |
| 428.15 |
0.007 60 |
0.008 30 |
0.217 2 |
0.214 5 |
0.581 4 |
0.582 5 |
| 438.15 |
0.009 40 |
0.009 90 |
0.271 9 |
0.269 7 |
0.571 3 |
0.571 5 |
| 448.15 |
0.011 60 |
0.011 80 |
0.336 4 |
0.335 3 |
0.560 7 |
0.560 2 |
|
表 11(c) 辛烷在沸点以上的密度和蒸气压
Table 11(c) Density and vapor pressure of octane above the boiling point |
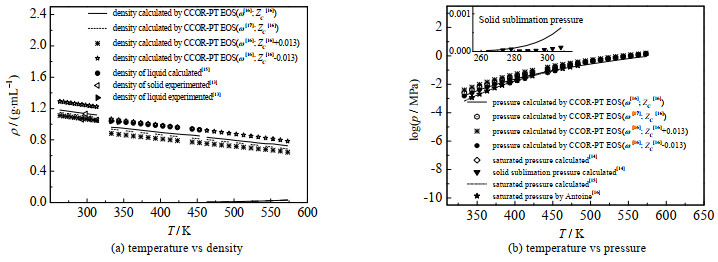
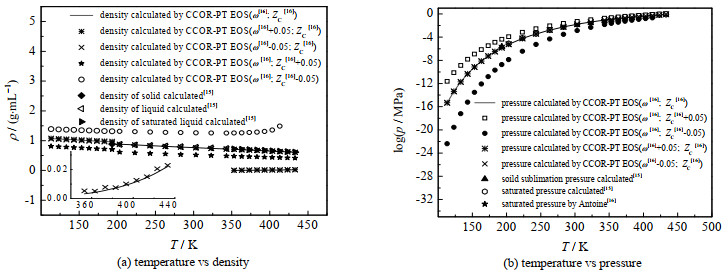
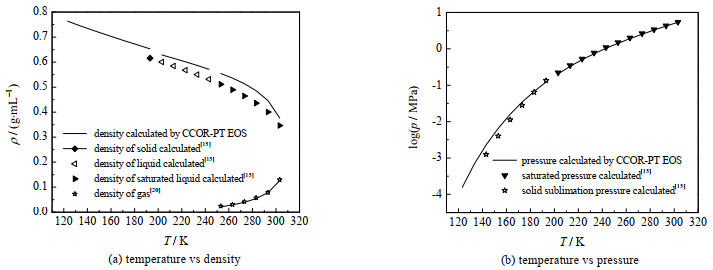
图 1中给出了本研究计算结果与文献值的比较,苯酚的偏心因子在不同文献中,数值有不同偏差:ω=0.426[16],ω=0.413 39[17],同时还显示了物性参数波动对计算结果的影响。后文将继续讨论并比较有关物性参数波动的影响。
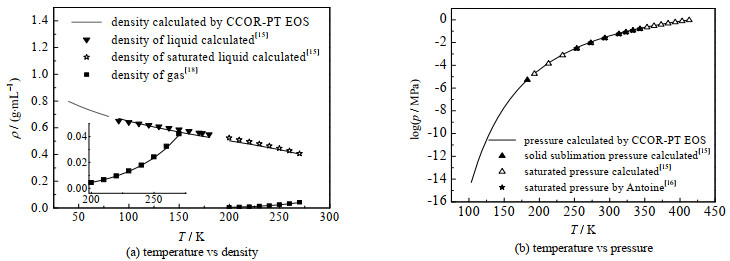
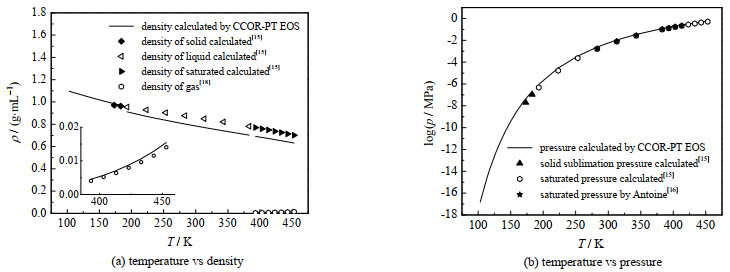
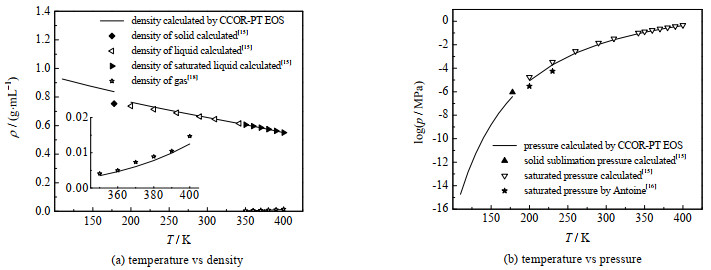
图 5给出了本研究计算结果与文献值的比较,同时还显示了物性参数波动对计算结果的影响。
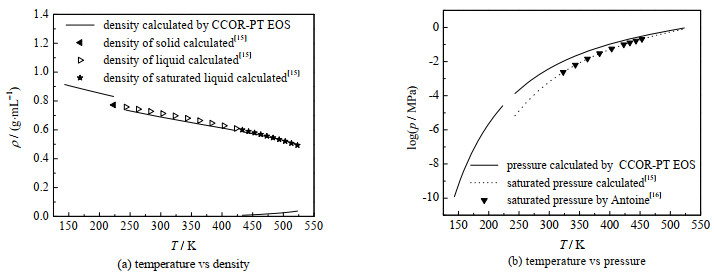
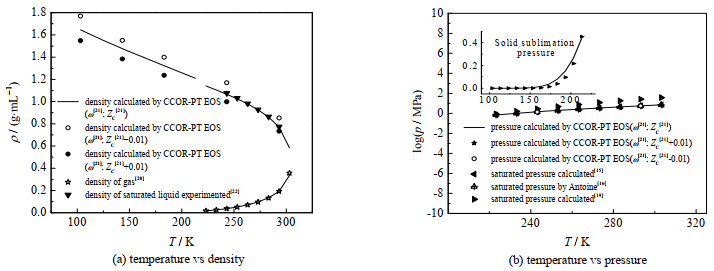
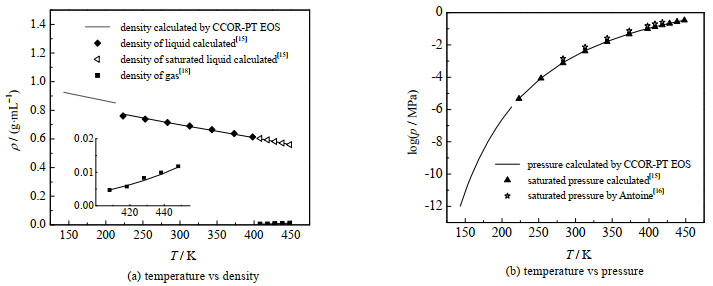
图 6给出了本研究计算结果与文献值的比较,同时还显示了物性参数波动对计算结果的影响。
4 物性参数对计算结果的影响
文献中能够检索到的临界压缩因子及偏心因子数据很有限,也未见有报道采用什么方法来判断它们的不确定度。通过实验来评估它们,在绝大多数工程实践中难以操作。工程上最常用的一个方法是通过基团贡献等近似方法来估算,那么这种估算出来的参数可能对最终计算结果会有多大程度的影响,是工程计算时必须要关注的一个问题,也是本研究企图揭示的一个问题。为了考察这一影响,对若干物质进行了调整临界压缩因子ZC及偏心因子ω的计算。
定义压力相对平均偏差为
|
$ {\text{RAD}}p = \sum {\left| {p' - p} \right|} /p/n $
|
(4) |
定义密度相对平均偏差为
|
$ {\text{RAD}}\rho = \sum {\left| {\rho ' - \rho } \right|} /\rho /n $
|
(5) |
上面两式中,p′、ρ′分别表示调整ω、ZC后使用CCOR-PT EOS计算得到的压力值、密度值,p、ρ作为对标基准,是使用检索得到的ω、ZC文献值代入CCOR-PT EOS计算得到的压力值、密度值。
以乙酸乙酯为例,袁渭康等[16]给出:ωlit=0.366,ZClit=0.255,下面表 12中给出ω、ZC波动对于压力及密度计算偏差的影响。
表 12
Table 12

表 12 乙酸乙酯压力、密度计算相对平均偏差与压缩因子、偏心因子的关系
Table 12 Relationship between relative mean deviation of pressure and density calculation of ethyl acetate and compression/acentric factors
| ω |
ZC |
RADp |
RADρ |
| ωlit+0.05 |
ZClit |
0.000 3 |
0.001 5 |
| ωlit |
ZClit+0.05 |
0.084 6 |
0.230 4 |
| ωlit−0.05 |
ZClit |
0.000 2 |
0.009 8 |
| ωlit |
ZClit−0.05 |
0.121 4 |
0.438 2 |
|
表 12 乙酸乙酯压力、密度计算相对平均偏差与压缩因子、偏心因子的关系
Table 12 Relationship between relative mean deviation of pressure and density calculation of ethyl acetate and compression/acentric factors |
从表 12、图 1、图 5以及图 6中可以看出,临界压缩因子ZC和偏心因子ω对计算结果都有影响。在临界压缩因子ZC和偏心因子ω两者之间比较,计算结果对临界压缩因子ZC更为敏感。
5 结论
(1) 长期以来,未见有状态方程方程可以跨界计算固-液-气三相。从上文的计算结果来看,CCOR-PT状态方程可以跨越固-液-气三相计算PVT性质,大大拓展了状态方程的应用范围。
(2) 和传统的立方型状态方程一样,CCOR-PT四次型状态方程可以得到解析解,因此其在使用的方便性方面也类同于传统的立方型状态方程。
(3) 对11个纯物质进行了计算,这11个物质中包括了有明显极性的丙酮、苯酚。从计算结果来看,使用CCOR-PT EOS状态方程计算极性和非极性物质固-液-气三相的PVT性质,总体上是可行的。对各相的计算,均给出了很合理的变化趋势,两相交界处附近的数值变化也符合相变规律,这表明该方程可以描述固相-流体相,是一个具有通用性的PVT计算工具。
(4) 液体、气体的计算精度要稍高于固体。对于固体,尤其是在低温条件下,当升华压力很低时,计算的满意度就比较差。也应该指出,虽然在全部计算中没有发现异常不合理的情况,对有的物质,该方程在计算的精度方面还存在一定的提升空间。
(5) 物性参数对CCOR-PT EOS的计算结果有重要影响,且对压力和密度2个计算结果大体上有同等程度的影响,临界压缩因子ZC对计算结果的影响明显大于偏心因子ω。
| 符号说明: |
| a, b, c ⎯ 状态方程中的参数 |
ω ⎯ 偏心因子 |
| d ⎯ 物质的参数 |
上标 |
| n ⎯ 计算点数 |
lit ⎯ 文献 |
| p ⎯ 压力,MPa |
′ ⎯ 调整w, Zc后用CCOR-PT EOS计算得到的参数 |
| T ⎯ 温度,K |
下标 |
| Vm ⎯ 摩尔体积,cm3·mol−1 |
C ⎯ 临界值 |
| Z ⎯ 压缩因子 |
RAD ⎯ 相对平均偏差 |
| ρ ⎯ 密度,g·mL−1 |
S ⎯ 固相 |
参考文献
| [1] |
KÖNIG M, WEBER SUTTER M. Applying common equations of state to three reference fluids: Water, carbon dioxide, and helium[J]. Chemie Ingenieur Technik, 2022, 94(4): 493-510. DOI:10.1002/cite.202100004 |
| [2] |
SOAVE G. Equilibrium constants from a modified Redlich-Kwong equation of state[J]. Chemical Engineering Science, 1972, 27(6): 1197-1203. DOI:10.1016/0009-2509(72)80096-4 |
| [3] |
PENG D Y, ROBINSON D B. A new two-constant equation of state[J]. Industrial & Engineering Chemistry Fundamentals, 1976, 15(1): 59-64. |
| [4] |
SAEKI S. Empirical determination of the isoenthalpic and isoentropic equations of state of polyethylene based on the pressure–volume–temperature–entropy equation of state[J]. Journal of Macromolecular Science, Part B, 2022, 61(6): 882-896. DOI:10.1080/00222348.2022.2116919 |
| [5] |
SAALI A, SAKHAEINIA H, SHOKOUHI M. Modeling the solubility of carbon dioxide and 1, 1, 1, 2-tetrafluoroethan-e in Ionic liquids using the van der Waals and Generic Redlich–Kwong equations of state[J]. Theoretical Foundations of Chemical Engineering, 2021, 55(1): 129-139. DOI:10.1134/S0040579521010127 |
| [6] |
SHAH V M, BIENKOWSKI P R, COCHRAN H D. Generalized quartic equation of state for pure nonpolar fluids[J]. AIChE Journal, 1994, 40(1): 152-159. DOI:10.1002/aic.690400117 |
| [7] |
薛新英. 宽广温度压力下流体与固体解析状态方程及应用的研究[D]. 成都: 电子科技大学, 2009.
XUE X Y. Research on analytical equation of state of simple fluid and solids over wide range of pressure and temperature [D]. Chengdu: University of Electronic Science and Technology of China, 2009.
|
| [8] | |
| [9] |
ZANG L Y, ZHU Q L, YUN Z. Extension of a quartic equation of state to pure polar fluids[J]. The Canadian Journal of Chemical Engineering, 2011, 89(3): 453-459. DOI:10.1002/cjce.20428 |
| [10] |
ZANG L Y, ZHU Q L, YUN Z. Critical properties prediction based on a quartic equation of state[J]. The Canadian Journal of Chemical Engineering, 2010, 88(6): 1003-1009. DOI:10.1002/cjce.20370 |
| [11] |
KIM H, LIN H M, CHAO K C. Cubic Chain-of-Rotators equation of state[J]. Industrial & Engineering Chemistry Fundamentals, 1986, 25(1): 75-84. |
| [12] |
PATEL N C, TEJA A S. A new cubic equation of state for fluids and fluid mixtures[J]. Chemical Engineering Science, 1982, 37(3): 463-473. DOI:10.1016/0009-2509(82)80099-7 |
| [13] |
CUNHA D L, COUTINHO J A P, DARIDON J L, et al. Experimental densities and speeds of sound of substituted phenols and their modeling with the prigogine flory patterson model[J]. Journal of Chemical and Engineering Data, 2013, 58(11): 2925-2931. DOI:10.1021/je4003256 |
| [14] |
BIDDISCOMBE D P, MARTIN J F. Vapour pressures of phenol and the cresols[J]. Transactions of the Faraday Society, 1958, 54: 1316-1322. DOI:10.1039/tf9585401316 |
| [15] |
JAMES O M. Perry's chemical engineers' hand book[M]. 8 th ed. Beijing: Science Press, 2001.
|
| [16] |
袁渭康, 王静康, 费维扬, 等. 化学工程手册[M]. 3版. 北京: 化学工业出版社, 2019.
YUAN W K, WANG J K, FEI W Y, et al. Chemical engineering handbook[M]. 3rd ed. Beijing: Chemical Industry Press, 2019.
|
| [17] | |
| [18] |
SMITH B D, SRIVASTAVA R. Thermodynamic data for pure compounds[M]. Amsterdam: Elsevier, 1986.
|
| [19] |
吴岐珅. 二氧化碳雪化分离特性研究[D]. 青岛: 中国石油大学(华东), 2020.
WU Q S. Research on carbon dioxide snowed separation characteristics [D]. Qingdao: China University of Petroleum(East China), 2020.
|
| [20] |
VARGAFTIK N B. Tables on the thermophysical properties of liquids and gases: In normal and dissociated states[M]. 2nd ed. Washington: Hemisphere, 1975.
|
| [21] |
POLING B E, PRAUSNITZ J M, O′CONNELL J P. The properties of gases and liquids[M]. New York: McGraw-Hill, 2001.
|
| [22] |
JENKIN C F. Dilatation and compressibility of liquid carbonic acid[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1920, 98(690): 170-182. |