2. 西安交通大学 能源与动力工程学院, 陕西 西安 710049
2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
高黏度流体的换热在石油化工行业中十分普遍,例如重油等油品的加热或冷却。这类流体在工业换热器中的操作雷诺数一般很低,流体运动呈层流状态,热量传递以分子导热为主,无论是对其加热或冷却都会遇到很大的困难[1-3]。缠绕管式换热器是一种典型的紧凑式换热器,其换热管束按螺旋线形状交错缠绕于芯筒与外筒之间,相邻两层换热管的螺旋方向相反,其具有耐高压、结构紧凑、单位体积换热面积大等优点[4-6]。但在相同的工况条件下,高黏度介质在这一类换热器中的综合换热性能与其他结构的换热器比较,特别是板式换热器,存在换热效率低、传热系数不高等缺点[7-8]。
针对高黏度介质在换热领域的表现,学者们主要做了以下的研究。任洪理等[9]通过实验得到了高黏度介质传热系数与流量、流体阻力及流速的经验关联式,证明高效换热器可以强化高黏度流体的换热性能;徐天华等[10]提出了一种新型管内插入物交叉锯齿带,对于提高管侧流体的换热性能效果显著;洪宇翔等[11]研究了粗糙换热管与管内插入物协同作用的强化传热机理,研究得到高黏度流体具有温差缓变特性,可以通过在管程中安置插入物来提高传热温差,加上粗糙管对近壁区流体的扰流,提高传热推动力;赵洪彬等[12]通过实验得到油在螺旋扁管换热器壳程冷却时的对流传热膜系数比其在管程冷却时高14%~46%;叶萌等[13]通过数值模拟研究了高黏度流体在弓形折流板开孔条件下的换热性能,结果表明折流板开孔后对流体产生扰动,压力分布与温度分布更加均匀;董春玲[14]通过数值模拟研究了螺旋板换热器的板间距、定距柱密度等参数对高黏度流体换热性能及流动性能的影响。
综上所述,针对高黏度流体在紧凑式换热器内强化换热的研究较为罕见。因此,针对缠绕管式换热器壳程独特的横掠管束流动形式,本研究提出了以多圆柱扰流为理论基础的壳程扰流元件,计算得到了扰流元件对缠绕管式换热器内高黏度介质的强化换热效果,并进一步研究了扰流元件结构参数对高黏度介质流动及换热性能的影响。
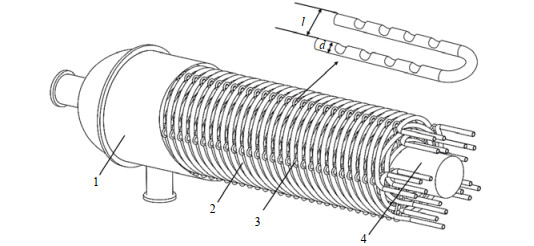
2 几何模型和数值方法 2.1 几何模型缠绕管式换热器模型与扰流元件的相对位置如图 1所示,模型由壳体、芯筒、换热管束和扰流元件组成,几何模型尺寸参照实验室换热器换热面积来设计。取1.5个缠绕单元作为计算域,缠绕层数为3层;芯筒直径95 mm,外筒直径190 mm,壳程总长度338 mm;换热管外壁面直径16 mm,螺距120 mm;相邻两管之间设置一根扰流件,扰流元件直径d为2~4 mm,扰流元件支脚之间的距离l为8~10 mm。传统结构不安装扰流元件,其余结构尺寸与新型结构相同。
|
图 1 缠绕管式换热器模型与扰流元件示意图 Fig.1 Schematic diagram of spiral-winding tube heat exchanger and disturbing device 1. shell of heat exchanger 2. heat exchange tube bundle 3.disturbing device 4. core tube of heat exchanger |
由于螺旋管束的影响,流场内部存在漩涡,RNG k-ε湍流模型对湍流黏度进行修正,考虑了平均流动中的旋转及旋流流动情况[15-18],因此本研究采用RNG k-ε模型。模型的控制方程如式(1)~(5)所示:
质量守恒方程:
| $ \frac{\partial }{{\partial {x_j}}}\left( {{u_j}} \right) = 0 $ | (1) |
| $ 动量守恒方程:\frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\eta _\text{eff}}\frac{{\partial {u_i}}}{{\partial {x_j}}}} \right) - \frac{{\partial p}}{{\partial {x_i}}} $ | (2) |
| $ 能量守恒方程:\frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}T} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\frac{\eta }{{Pr}} + \frac{{{\eta _\text{tur}}}}{{{\sigma _t}}}} \right)\frac{{\partial T}}{{\partial {x_j}}}} \right] + {S_T} $ | (3) |
| $ 湍动能k方程:\frac{\partial }{{\partial {x_j}}}\left( {\rho k{u_j}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\eta + \frac{{{\eta _\text{tur}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + \rho \varepsilon $ | (4) |
湍动能耗散
| $ \frac{\partial }{{\partial {x_j}}}\left( {\rho \varepsilon {u_j}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\eta + \frac{{{\eta _\text{tur}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{\varepsilon }{k}\left( {{G_k}{C_{1\varepsilon }} - {C_{2\varepsilon }}\rho \varepsilon } \right) $ | (5) |
式中:ρ为流体密度,kg·m−3;ηeff为有效动力黏度,Pa·s;ηtur为湍流动力黏度,Pa·s;
模拟介质为导热油,由于高黏度物质物性随温度变化较大,其物性参数拟合为温度相关的函数,物性参数如式(6)~(9)所示[19];入口速度为0.2~1 m·s−1,入口温度为293 ℃;出口条件设置为压力出口;壁面温度为333 ℃;壁面函数为标准壁面函数;采用有限体积法对方程组和边界条件进行数值求解;采用Coupled算法进行压力与速度的耦合。
| $ \rho = - 0.59 \times T + {1_{}}038.1 $ | (6) |
| $ {c_p} = 5.045 \times T + 414.02 $ | (7) |
| $ \lambda {\text{ = 0}}{\text{.00}}{{\text{0}}_{}}{\text{05}} \times T - {0.000_{}}{000_{}}2 \times {T^2} + {0.123_{}}6 $ | (8) |
| $ \eta {\text{ = }}1 \times {10^{22}} \times {T^{ - 9.616}} $ | (9) |
式中:cp为比定压热容,J·(kg·K)−1;λ为导热系数,W·(m·K)−1。
普朗特数反映了流动边界层与热边界层的相对大小,如式(10)所示。对于高黏度的油类物质,Pr一般在102~103数量级,导热油在本研究计算工况范围内Pr为253.53~280.72。
| $ Pr = \frac{{{c_p}\eta }}{\lambda } = \frac{v}{a} $ | (10) |
式中:a为热扩散系数,m2·s−1;v为流体的运动黏度,m2·s−1。
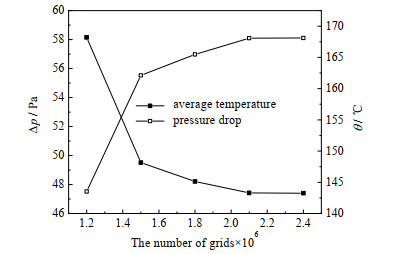
使用多面体网格进行网格划分,并对扰流元件及换热管处的网格进行加密。以换热器出口的平均温度及出入口的压降为指标,对网格进行无关性验证,如图 2所示为网格数量对平均温度θ和压降的影响。
|
图 2 网格无关性验证 Fig.2 Verification of grid independence |
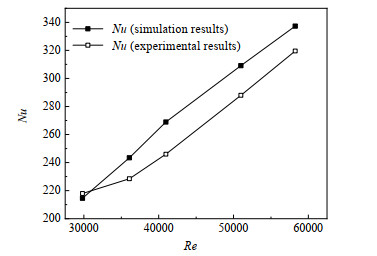
如图 3所示为数值计算得到的努赛尔数Nu与文献[20]中数据的对比,数值模拟模型采用与文献中相同的工况条件,计算得到平均偏差为5.67%,数值模拟结果较为准确,后续的计算均基于该数值模型和算法。计算偏差主要是由于数值模拟假设除换热管壁面外其余壁面为绝热壁面,导致数值模拟得到的努赛尔数偏高。图中,Re为雷诺数。
|
图 3 实验与模拟结果对比 Fig.3 Comparison of experimental and simulation results |
考虑缠绕管式换热器的综合性能,以努赛尔数Nu、流动摩擦因子f、综合换热性能PEC值为目标函数进行研究,计算公式如下:
| $ h = \frac{{{q_m}{c_p}\left( {{T_{{\text{out}}}} - {T_{{\text{in}}}}} \right)}}{{A\Delta {T_{\text{m}}}}} $ | (11) |
| $ \Delta {T}_{\text{m}}\text{=}({T}_{\text{out}}-{T}_{\text{in}}){\text{/ln}}_{}\text{(}\frac{{T}_{\text{w}}-{T}_{\text{in}}}{{T}_{\text{w}}-{T}_{\text{out}}}) $ | (12) |
| $ Nu = \frac{{h{D_{\text{h}}}}}{\lambda } $ | (13) |
| $ f = \frac{{{\text{2}}\Delta p{D_{\text{h}}}}}{{\rho v_{\max }^{\text{2}}H}} $ | (14) |
| $ {\text{PEC}} = {{Nu} \mathord{\left/ {\vphantom {{Nu} {{f^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}}} \right. } {{f^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}} $ | (15) |
式中:h为传热系数,W·(m2·K)−1;qm为壳侧流体质量流量,kg·s−1;A为换热面积,m2;ΔTm为对数平均温差,K;Dh为壳程当量直径;vmax为壳程流体最大流速,m·s−1;H为换热器长度,m;下标w、in、out分别表示壁面、进口、出口;Δp为进出口压差,Pa。
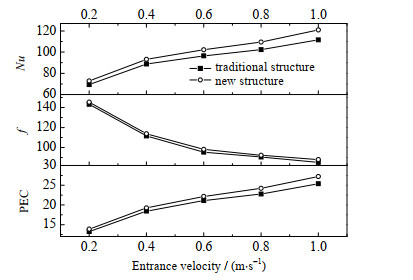
3 结果讨论将直径为3 mm,支脚之间的距离为10 mm的扰流元件作为原始结构,与传统结构进行对比计算,计算结果如图 4所示。计算结果表明:在相同的进口工况下,添加扰流元件的缠绕管式换热器壳侧努塞尔数相比于传统结构可提高5.1% ~8.4%,摩擦因子升高了1.3%~3.3%,综合换热性能可提高4.6%~5.2%。在此基础上分别研究了扰流元件直径d及支脚距离l对目标参数的影响规律,对进一步改善高黏度介质在缠绕管换热器内的流动及换热性能提供理论依据。
|
图 4 传统结构与新型结构性能参数对比 Fig.4 Comparison of performance parameters between traditional and new structures |
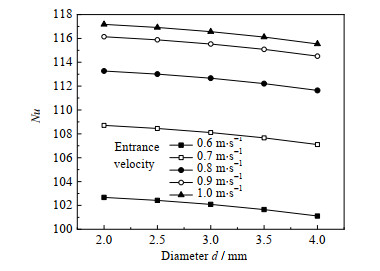
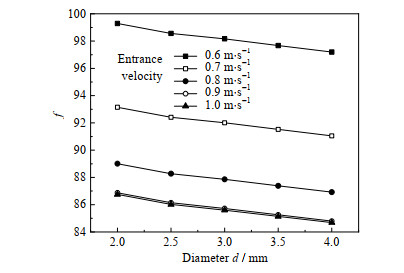
如图 5和6所示分别为是不同壳程入口速度下Nu及摩擦因子f随扰流元件直径的变化规律。从图中可以得到,随着扰流元件直径的增大,高黏度介质在缠绕管式换热器内的Nu及摩擦因子f均呈现逐渐降低的趋势,且随着壳程入口流速的升高,Nu逐渐升高而摩擦因子f逐渐降低。
|
图 5 Nu随直径的变化规律 Fig.5 Variation of Nu as a function of diameter |
|
图 6 f随直径的变化规律 Fig.6 Variation of f as a function of diameter |
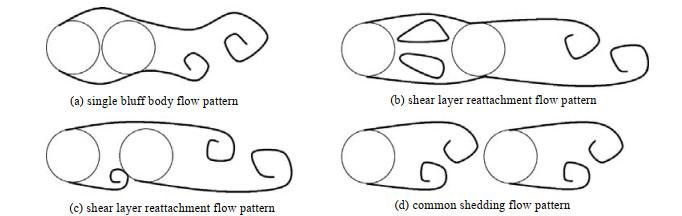
缠绕管式换热器壳程介质在管束间的流动形式与圆柱扰流运动类似,沿圆柱表面流动的流体在到达圆柱顶点附近会发生边界层分离,然后在圆柱后缘上下两侧形成周期性地漩涡脱落。对于多圆柱扰流,由于圆柱之间相互影响,会形成如图 7所示的流动形态。当相邻两圆柱之间的距离很小时,分离形成的两个剪切层之间的距离也很小,流动行为与单一的圆柱类似,如图 7(a)所示;随着圆柱之间距离的增加,上游圆柱形成剪切层重新附着下游圆柱表面,圆柱之间的流体呈对称分布或非对称分布,如图 7(b)(c)所示;当两个圆柱之间的距离很大时,圆柱之间的相互作用影响很小,在各个圆柱之后都形成了漩涡脱落,如图 7(d)所示。而扰流元件的存在可以改变高黏度介质在管束间的流动形式,从而有效提高其综合换热效果。
|
图 7 多圆柱扰流流动形式 Fig.7 Flow patterns of multi cylinder turbulence |
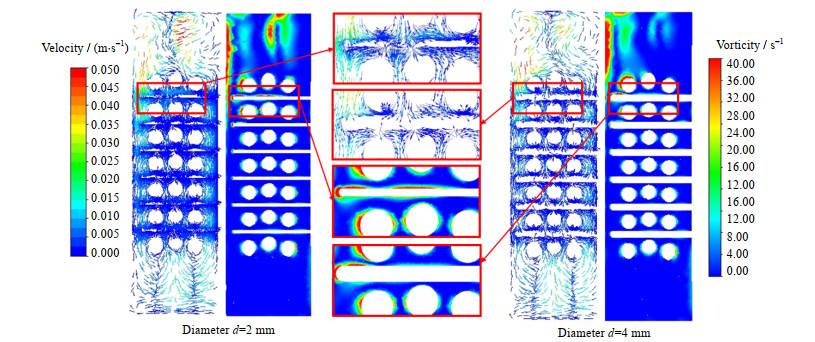
如图 8所示为不同结构下,在X=10 mm横截面上的速度矢量图及涡量云图。当扰流件的直径较小时,对上游圆柱漩涡脱落的流动行为影响较小,流体在管束之间的速度及涡量较高,干扰流动边界层及热边界层,进而增强流体和壁面之间的对流换热,这有利于强化传热,但是流体在此处的碰撞也会增大阻力损失;随着扰流元件直径的增大,流体横掠上游管束后形成的剪切层重新附着在扰流元件上,继续向下游流动,只有部分流体进入换热管束与扰流元件之间的空隙内,不利于主流区与换热管近壁面处流体的混合,因此随着扰流元件直径的增大,导热油在缠绕管换热器壳程的流动性能逐渐改善,而其换热效果不断恶化。扰流元件直径为2 mm时该参考截面的平均涡量值为5.48 s−1,直径为4 mm时该参考截面的平均涡量值为5.04 s−1,平均涡量相对降低了8.03%。
|
图 8 速度矢量图及涡量云图(X=10 mm) Fig.8 Velocity vector graphics and vorticity contours (X=10 mm) |
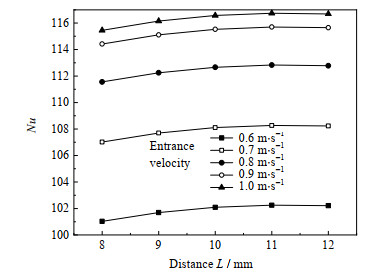
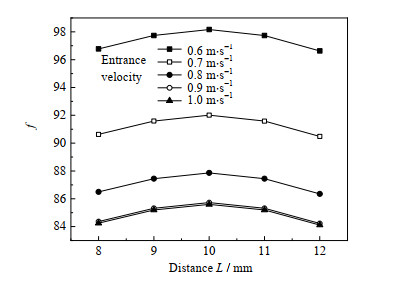
如图 9和10所示分别为不同壳程入口速度下Nu及摩擦因子f随扰流元件支脚距离l的变化规律。从图中可以得到,随着扰流元件距离的增大,高黏度介质在缠绕管式换热器内的Nu及摩擦因子f表现出先升高后降低的趋势。
|
图 9 Nu随距离的变化规律 Fig.9 Variation of Nu as a function of distance |
|
图 10 f随距离的变化规律 Fig.10 Variation of f as a function of distance |
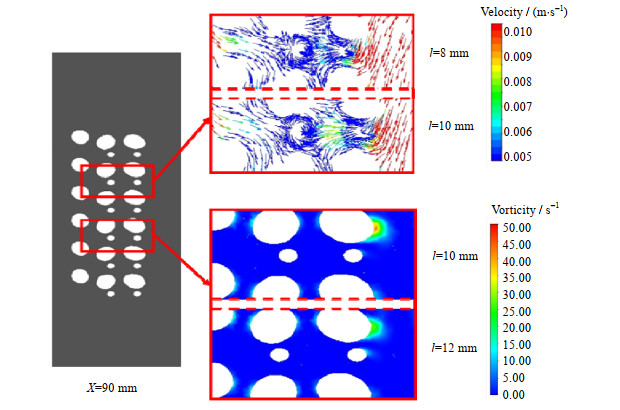
如图 11所示为不同结构在X=90 mm横截面上的速度矢量图及涡量云图。从图中可以得到当扰流元件支脚距离由8 mm增加到10 mm时,管束与管束、管束与扰流件之间流体流速更高,流动形态更加复杂,这是因为随着支脚距离的增大,流体流经扰流件在下游区域形成的扰动范围更大,有利于壳程介质沿径向的流动及主流区与管壁附近流体之间的混合,流体对管束壁面的冲刷可以降低热边界层,提高换热效率,但同时也会增大其压降损失。随着扰流元件支脚距离进一步增大,其逐渐向管壁靠近,抑制了上游管束的漩涡脱落,从图 11中可以看到支脚距离由10 mm增加至12 mm时,管束周围的涡量值明显降低,因此壳程阻力损失又呈现降低的趋势,壳程的换热性能也相应下降,扰流元件支脚距离在12 mm时,换热器壳程换热性能较高,且流动阻力损失较低。
|
图 11 速度矢量图及涡量云图(X=90 mm) Fig.11 Velocity vector graphics and vorticity contours (X=90 mm) |
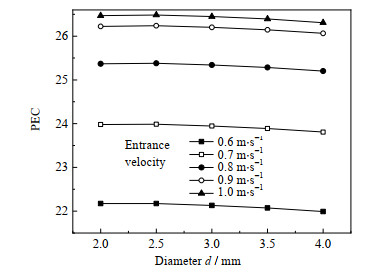
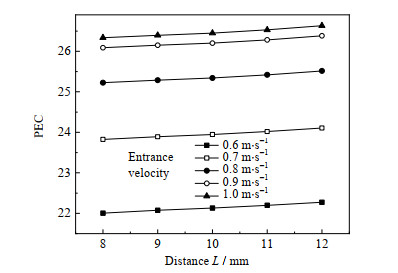
进一步讨论了扰流元件结构参数d和l对高黏度介质导热油在缠绕管式换热器内的综合换热性能,以PEC值作为综合换热性能指标。如图 12、13所示分别为PEC值在各工况下随扰流元件结构参数的变化趋势,得到换热器的综合换热性能随扰流件直径d的增加逐渐降低,随扰流件支脚距离l的增加而不断升高,可据此对高黏度流体在缠绕管式换热器的表现进一步优化。
|
图 12 PEC随直径的变化规律 Fig.12 Variation of PEC as a function of diameter |
|
图 13 PEC随距离的变化规律 Fig.13 Variation of PEC as a function of distance |
研究了高黏度流体在缠绕管式换热器的流动性能及换热性能,得到的结论如下:
(1) 扰流元件可改善高黏度介质在缠绕管式换热器壳程的流动形式,使得高黏度介质在紧凑式换热器中同样可以达到理想的换热效果。在相同的进口工况下,添加扰流元件的缠绕管式换热器壳侧努塞尔数相比于传统结构可提高5.1%~8.4%,摩擦因子升高1.3%~3.3%,综合换热性能可提高4.6%~5.2%;
(2) 随着扰流元件直径的增大,高黏度介质在缠绕管式换热器内的Nu及摩擦因子f均呈现逐渐降低的趋势;随着扰流元件支脚距离的增大,高黏度介质在缠绕管式换热器内的Nu及摩擦因子f均呈现先升高后降低的趋势;
(3) 换热器的综合换热性能随扰流件直径的增加逐渐降低,随扰流件支脚距离的增加而不断升高。
| [1] |
石帅. 滑油冷却器强化换热与阻力特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. SHI S. Research on heat transfer enhancement and friction characteristic of lubricating oil cooler [D]. Harbin: Harbin Engineering University, 2013. |
| [2] |
彭婷. 基于黏弹性流体的微型换热器强化传热机理研究[D]. 南昌: 南昌大学, 2012. PENG T. The research on the heat transfer enhancement mechanism of micro heat exchanger based on viscoelastic fluid [D]. Nanchang: Nanchang University, 2012. |
| [3] |
陈亚平, 徐礼华, 周强泰. 适用于高黏性流体冷却的新型热虹吸式螺旋板式换热器[J]. 石油化工设备, 1997(6): 7-9. CHEN Y P, XU L H, ZHOU Q T. A novel thermosiphon spiral plate heat exchanger for cooling high viscous fluids[J]. Petro-Chemical Equipment, 1997(6): 7-9. |
| [4] |
沃联邦. 黏性流体换热器[J]. 医药设计, 1983(5): 1-2. WO L B. Heat exchanger of viscous fluid[J]. Chemical and Pharmaceutical Engineering, 1983(5): 1-2. |
| [5] |
肖娟, 简冠平, 王家瑞, 等. 缠绕管式换热器性能及应用研究进展[J]. 化工机械, 2016, 43(4): 423-428. XIAO J, JIAN G P, WANG J R, et al. Progress in performance and application study for wound-tube heat exchanger[J]. Chemical Engineering & Machinery, 2016, 43(4): 423-428. DOI:10.3969/j.issn.0254-6094.2016.04.001 |
| [6] |
于清野. 缠绕管式换热器计算方法研究[D]. 大连: 大连理工大学, 2011. YU Q Y. Research on calculation method for helical wound coil tube heat exchangers [D]. Dalian: Dalian University of Technology, 2011. |
| [7] |
王斯民, 简冠平, 肖娟, 等. 缠绕管式换热器结构参数多目标优化数值模拟研究[J]. 西安交通大学学报, 2017, 51(5): 9-15. WANG S M, JIAN G P, XIAO J, et al. Multi-objective optimization on the structural parameters of spiral wound heat exchanger[J]. Journal of Xi'an Jiaotong University, 2017, 51(5): 9-15. |
| [8] |
尹接喜, 李清海, 施德强, 等. 缠绕管换热器并管传热模型及实验[J]. 清华大学学报(自然科学版), 2000, 40(6): 73-75, 79. YIN J X, LI Q H, SHI D Q, et al. Heat transfer model land experiment for paired-tubes wound-tube heat exchangers[J]. Journal of Tsinghua University (Science and Technology), 2000, 40(6): 73-75, 79. DOI:10.3321/j.issn:1000-0054.2000.06.021 |
| [9] |
任洪理, 张国磊, 张艳霞, 等. 板式换热器在高黏度流体强化传热的工程研究[J]. 化工设计, 2009, 19(2): 20-22, 31, 1. REN H L, ZHANG G L, ZHANG Y X, et al. Engineering research on heat transfer enhancement of plate heat exchanger in high viscosity fluid[J]. Chemical Engineering Design, 2009, 19(2): 20-22, 31, 1. DOI:10.3969/j.issn.1007-6247.2009.02.006 |
| [10] |
徐天华, 崔乃瑛, 谭盈科. 管内插入物强化高黏液体传热[J]. 化学工程, 1988(6): 7-15, 2. XU T H, CUI N Y, TAN Y K. Heat transfer enhancement of high viscosity liquid by tube inserts[J]. Chemical Engineering, 1988(6): 7-15, 2. |
| [11] |
洪宇翔, 邓先和, 张连山. 管间高黏度流体的有效传热温差缓变特性[J]. 化工学报, 2012, 63(2): 441-447. HONG Y X, DENG X H, ZHANG L S. Slow change of effective heat transfer temperature difference of highly viscous fluid on shell side[J]. CIESC Journal, 2012, 63(2): 441-447. DOI:10.3969/j.issn.0438-1157.2012.02.015 |
| [12] |
赵洪彬. 高黏度流体传热强化研究[D]. 广州: 华南理工大学, 2011. ZHAO H B. Investigation on heat transfer enhancement of fluids with high viscosity [D]. Guangzhou: South China University of Technology, 2011. |
| [13] |
叶萌, 喻九阳, 郑小涛, 等. 高黏度流质下管壳式折流板开孔换热器换热性能的数值模拟[J]. 当代化工, 2015, 44(1): 212-214. YE M, YU J Y, ZHENG X T, et al. Numerical simulation on the performance of the heat exchanger with perforated baffle in high viscosity fluid[J]. Contemporary Chemical Industry, 2015, 44(1): 212-214. |
| [14] |
董春玲. 高黏性流体螺旋板换热器传热特性与结构研究[D]. 大庆: 东北石油大学, 2013. DONG C L. Research on heat transfer and structures of high viscosity fluid in spiral heat exchanger [D]. Daqing: Northeast Petroleum University, 2013. |
| [15] |
吴志勇, 陈杰, 浦晖, 等. LNG绕管式换热器壳侧过热态流动的数值模拟[J]. 煤气与热力, 2014, 34(8): 6-11. WU Z Y, CHEN J, PU H, et al. Numerical study on over heat flow in the shell side of spiral wound heat exchanger[J]. Gas & Heat, 2014, 34(8): 6-11. |
| [16] |
文键, 杨辉著, 杜冬冬, 等. 螺旋折流板换热器换热强化的数值研究[J]. 西安交通大学学报, 2014, 48(9): 43-48. WEN J, YANG H Z, DU D D, et al. Numerical simulation for heat enhancement of a heat exchanger with helical baffles[J]. Journal of Xi'an Jiaotong University, 2014, 48(9): 43-48. |
| [17] |
文键, 杨辉著, 王斯民, 等. 旋梯式螺旋折流板换热器优化结构的数值模拟[J]. 西安交通大学学报, 2014, 48(11): 8-14. WEN J, YANG H Z, WANG S M, et al. Numerical simulation for configuration optimization of heat exchanger with helical baffles[J]. Journal of Xi'an Jiaotong University, 2014, 48(11): 8-14. |
| [18] |
王福军. 计算流体动力学分析——CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. WANG F J. Computational fluid dynamics analysis-theory and application of CFD software[M]. Beijing: Tsinghua University Press, 2004. |
| [19] |
栾志坚. 新型板式换热器内高黏性流体传热与流动特性研究[D]. 济南: 山东大学, 2009. LUAN Z J. Research on heat transfer and flow characteristics of high viscosity fluid in new PHE [D]. Jinan: Shandong University, 2009. |
| [20] |
REN Y, CAI W, JIANG Y. Numerical study on shell-side flow and heat transfer of spiral-wound heat exchanger under sloshing working conditions[J]. Applied Thermal Engineering, 2018, 134(7): 287-297. |




