纳米流体是以一定的形式和比例在液体工质中添加纳米级别的金属或非金属氧化物颗粒,形成均匀且稳定的固液混合物[1]。大量研究表明,纳米流体比传统纯工质具有更高的导热系数,在传热领域具有广阔的应用前景。一元纳米流体由于只含有一种纳米粒子,只具有某种颗粒的特殊性质[2-4]。为了使纳米流体拥有更多的优越性能,Turcu等[5]提出了混合纳米流体的概念。它是由2种及以上不同性质的纳米粒子混合而成的均匀悬浮的固液混合物。由于混合纳米流体是由不同种类的纳米粒子组成,可同时拥有不同种类粒子的性质,得到较好的传热网络和流变性能。通过课题组前期的研究[6-7],观察X射线衍射(XRD)图谱发现通过两步法制备的混合纳米流体不发生化学反应,仅通过粒子间、粒子与流体分子间的物理排列,形成了一层致密的热传导通道,降低了界面热阻,使导热系数增大。由于混合纳米流体的优越热物性能,近十几年来被越来越多的学者用于各行各业。
混合纳米流体不仅受体积分数、温度、基液种类、粒子种类及粒径等因素影响,还受粒子组合的质量比的影响[8]。选择合适的纳米粒子组合及质量比对纳米流体的传热效率和热物性很重要[9]。Hamid等[10]研究了TiO2-SiO2/乙二醇-水混合纳米流体的粒子质量比对导热系数和黏度的影响,发现当粒子质量比为50:50时,导热系数最低;而当粒子质量比为40:60和80:20时导热系数均有较大增幅。有些研究,如文献[11-13],指出混合纳米流体的导热系数和黏度并不总是随体积分数的增大而增大,在混合纳米流体中由于各粒子的密度不同,随着粒子数量增多,重力会使粒子沉淀,失去纳米流体的优良性质。因此,混合纳米流体的导热系数和黏度变化是否遵循常规纳米流体的相应变化规律,还需要更多关于不同粒子组合的纳米流体实验来验证。
在对流传热过程中,一方面纳米流体中的粒子粒径较小,降低了由流动产生的腐蚀及压降等,运行时相对微米或毫米级别的颗粒更稳定;另一方面,纳米流体的导热系数比基液高,使它在对流传热中起到强化作用[14-17]。但是,对于纳米流体强化对流传热性能的原因还存在争议。Ali等[18]研究了SiO2/水纳米流体在紊流区的传热性能,当体积分数为0.007% 时,与纯水比,对流传热系数增大了27%,并指出纳米流体管内对流传热增强是由于导热系数增强及粒子的无序微运动导致的。还有一种假设,随着纳米流体黏度增大,对流传热系数增大。因为纳米流体的黏度随颗粒质量浓度的增加而显著增加,因此在固定雷诺数下,纳米流体的质量流量总是超过基液的质量流量。但是,Mehrali等[19]实验研究了石墨烯纳米流体在恒热流密度加热下的对流传热性能,指出在固定质量流量下纳米流体的对流传热系数增大[20]。Bahiraei等[21]指出粒子迁移作用会影响对流传热系数,他指出布朗扩散和由温差引起的热泳运动会影响管内对流传热性能。但是,关于混合纳米流体中粒子迁移作用对对流传热的研究还不多。
鉴此,为了研究混合纳米流体中粒子迁移作用对传热的影响,本研究以Al2O3-CuO/水混合纳米流体流经恒热流密度加热的光滑铜管为研究对象,研究不同体积分数和温度下其黏度与导热系数的变化规律;探究粒子迁移作用对层流及紊流区对流传热系数的影响;最后,从微观角度揭示纳米流体对流传热的强化机制。
2 实验材料与方法 2.1 混合纳米流体制备及参数测量纳米粒子采用粒径分别为20 nm的Al2O3和40 nm的CuO粒子,基液为去离子水,热物性参数如表1所示[22]。虽然CuO纳米粒子的导热系数高于Al2O3的,但是由于密度大,体积分数越大越影响纳米流体的稳定性,且CuO易氧化。而Al2O3的化学稳定好,对于氧化物而言导热系数也不低,因此选用Al2O3和CuO质量比为80:20。各参数选取的依据是基于作者前期的研究结果,Ma等[23]研究了Al2O3和CuO的质量比对Al2O3-CuO/乙二醇-水纳米流体的导热系数的影响,发现在质量比为80:20时由于粒子间的协同作用使纳米流体内部的传热网络最佳,因此导热系数最高。采用两步法分别制备体积分数φ为0.01%、0.02%、0.03%的Al2O3-CuO/水混合纳米流体,其体积分数由式(1)计算:
|
|
表 1 实验材料与参数 Table 1 Experimental materials and parameters |
| $ \varphi {\text{ = }}\frac{{\frac{{{m_{{\text{NP1}}}}}}{{{\rho _{{\text{NP1}}}}}} + \frac{{{m_{{\text{NP2}}}}}}{{{\rho _{{\text{NP2}}}}}}}}{{\frac{{{m_{{\text{NP1}}}}}}{{{\rho _{{\text{NP1}}}}}} + \frac{{{m_{{\text{NP2}}}}}}{{{\rho _{{\text{NP2}}}}}} + \frac{{{m_{_{{\text{bf}}}}}}}{{{\rho _{{\text{bf}}}}}}}} \times 100\% $ | (1) |
式中:mNP1、mNP2分别为Al2O3、CuO纳米粒子的质量,kg;mbf为基液的质量,kg;ρNP1、ρNP2分别为Al2O3、CuO纳米粒子的密度,kg⋅m−3;ρbf为基液的密度,kg⋅m−3。
如图1所示为Al2O3-CuO/水混合纳米流体两步法的制备流程及透射电镜图(TEM)。所有体积分数下Al2O3和CuO粒子的质量比均固定为80:20,由式(1)计算所要称取的Al2O3和CuO纳米粒子的质量,放置于含去离子水的烧杯中搅拌。为了获取稳定悬浮的纳米流体,先用磁力搅拌器(JKI-MSH-HS,上海)搅拌15 min,再用超声振荡仪(CP-2010GTS,北京)进行超声波振动1 h。另外,选取体积分数为0.01% 的Al2O3-CuO/水混合纳米流体进行TEM图像分析。结合Image J软件计算TEM图像中团簇体的平均尺寸,得到平均粒径为65 nm,且粒子分散均匀。在同一体积分数下由于Al2O3粒子的数量远大于CuO粒子,从TEM图可以看到,棒状Al2O3粒子填充在由球形CuO粒子形成的缝隙中,形成致密的界面层,即传热网络良好的导热通道。因此,通过该方法可以得到分散均匀且团聚尺寸小的纳米流体,其他体积分数的纳米流体制备也按该方法进行。

|
图 1 两步法制备Al2O3-CuO/水混合纳米流体流程及TEM图 Fig.1 Flow chart of the two-step method for Al2O3-CuO/water hybrid nanofluids preparation and a TEM image of the prepared sample |
分别采用型号为Brookfield DV3T黏度仪和Hotdisk 2500S热常数分析仪测量混合纳米流体的黏度μ和导热系数λ。黏度仪和热常数分析仪的不确定度(Uμ和Uλ)由式(2a)、(2b)计算[24]:
| $ {U_\mu } = \sqrt {{{\left( {\frac{{\Delta t}}{t}} \right)}^2} + {{\left( {\frac{{\Delta \mu }}{\mu }} \right)}^2}} $ | (2a) |
| $ {U_\lambda } = \sqrt {{{\left( {\frac{{\Delta t}}{t}} \right)}^2} + {{\left( {\frac{{\Delta \lambda }}{\lambda }} \right)}^2}} $ | (2b) |
式中:t为测量温度,℃;
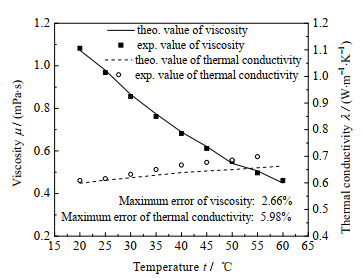
由式(2a)、(2b)计算得出,黏度和导热系数测量的最大不确定度分别为1.11% 和3.04%。为确保测量值的准确性,测量混合纳米流体黏度前先使用去离子水对仪器精确度进行检查。在20~60 ℃下,测量去离子水黏度和导热系数与标准值进行对比,为保证测量结果的精确性,每个条件下测量3次取平均值。如图2所示为去离子水的实验测量值与标准值[25]对比。其中,黏度和导热系数与标准值的最大误差分别为1.05% 和3%,这表明实验测量误差在仪器的不确定度范围内,从而验证了数据的精确性。一般来说水基混合纳米流体的黏度及导热系数与水的处于一个数量级,仪器完全可用于混合纳米流体参数测量。
|
图 2 去离子水导热系数及黏度测量值与标准值对比 Fig.2 Comparison of measured and theoretical values of thermal conductivity and viscosity (deionized water) |
Al2O3-CuO/水混合纳米流体的密度
| $ {\rho _{{\text{nf}}}} = {\varphi _{{\text{NP1}}}}{\rho _{{\text{NP1}}}} + {\varphi _{{\text{NP2}}}}{\rho _{{\text{NP2}}}} + (1 - {\varphi _{{\text{NP1}}}} - {\varphi _{{\text{NP2}}}}){\rho _{{\text{bf}}}} $ | (3) |
| $ {c_{{\text{nf}}}} = \frac{{{\varphi _{{\text{NP1}}}}{\rho _{{\text{NP1}}}}{c_{{\text{NP1}}}} + {\varphi _{{\text{NP2}}}}{\rho _{{\text{NP2}}}}{c_{{\text{NP2}}}} + (1 - {\varphi _{{\text{NP1}}}} - {\varphi _{{\text{NP2}}}}){\rho _{_{{\text{bf}}}}}{c_{{\text{bf}}}}}}{{{\rho _{{\text{nf}}}}}} $ | (4) |
式中:φNP1、φNP2分别为Al2O3、CuO纳米流体的体积分数; cNP1、cNP2分别为Al2O3、CuO纳米流体的比热容,kJ⋅kg−1⋅K−1;cbf为基液的比热容,kJ⋅kg−1⋅K−1。
虽然许多经验关联式可用于预测一元及混合纳米流体的密度和热容量,但通过混合理论计算的式(3)和(4)与实验结果吻合较好,在文献[26]中对其精确度有较多报道。
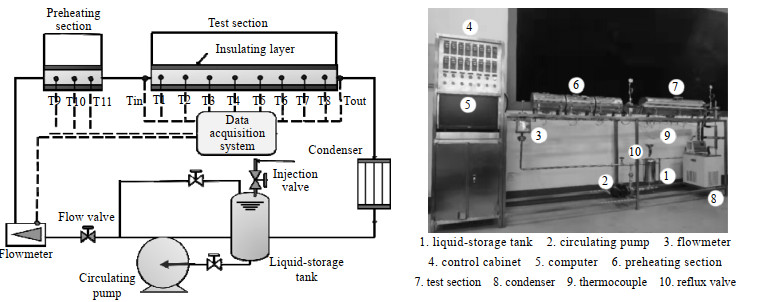
2.2 对流传热实验过程混合纳米流体管内对流传热实验如图3所示。系统主要包括实验段、预热段、数据采集系统、冷凝系统和循环系统组成。该实验系统可实现均匀热流密度加热。加热段采用Φ 8 mm×1 000 mm的光滑铜管,外表面包裹保温棉以防止热量散失,如图3中的6、7部分所示,保温棉采用金属壳覆盖,进一步减少热能损耗。测试部分沿加热铜管表面均匀布置8个测温点用于监测外壁温,另外流体进出口各设置一个测温点。预热部分加热铜管表面布置3个测温点用于观察温度的稳定情况。温度及流量值由数据采集仪实时采集,控制器实时监控实验环境。实验首先以水作为参考工质,验证系统的精度及实验数据的准确性。其次,研究Al2O3-CuO/水混合纳米流体在不同体积分数下对层流(Re:0~2 300)及紊流(Re:4 000~8 000)对流传热的影响规律,探究粒子迁移作用对传热的影响机制。
|
图 3 混合纳米流体对流传热实验系统 Fig.3 Experimental system of convective heat transfer with hybrid nanofluids |
实验段采用电加热方式,在加热管四周均匀缠绕电阻丝,以获得恒定热流密度。根据圆管内对流换热计算,单位面积的有效热流密度可表示为
| $ q = \frac{P}{{\pi {D_i}L}} = \frac{{{P_{{\text{total}}}} - {P_{{\text{loss}}}}}}{{\pi {D_i}L}} $ | (5) |
式中:q为热流密度,W⋅m−2;Di和L分别为圆管内径和长度,m;P和Ptotal分别为有效加热功率和总加热功率,W;其中Ptotal由施加在加热丝两端的电流和电压相乘计算,Ploss为保温层与环境的对流及辐射散热损失,W;Ploss按总功率3% 计算。本实验采取的有效加热功率约为24 W,热流密度为1.85×103 W⋅m−2。
实验段纳米流体在圆管中对流传热系数为
| $ h = \frac{q}{{{t_{{\text{w}},i}} - {t_{\text{f}}}}} $ | (6) |
式中:h为纳米流体在圆管中对流传热系数,W⋅m−2⋅K−1;tf和tw,i分别为流体平均温度和管内壁面的平均温度,℃。
实验参数的不确定性如表2所示。
|
|
表 2 实验参数的不确定度 Table 2 Uncertainty of experimental parameters |
首先,以去离子水为参考工质验证管内对流传热实验系统的精确性。对于纯水的管内流动换热,已经有了非常成熟的换热系数预测模型。层流和紊流下Nusselt数的关联式分别计算如下[27]:
| $ 层流时:\;\;\;\;\;\;\;\;\;N u=C\left(\operatorname{Re} P r \frac{D_{\mathrm{i}}}{L}\right)^{1 / 3}\left(\frac{\mu_{\mathrm{f}}}{\mu_{\mathrm{w}}}\right)^{0.14} $ | (7) |
式中:Pr为普朗特数;C为常数,与边界条件有关。恒壁温边界条件下,C取1.86;恒热流密度下,C取2.232。μf和μw分别为工质达到流体温度和壁温时的黏度(mPa⋅s)。
| $ 紊流时:\;\;\;\;\;\;\;\;\; Nu = 0.023R{e^{0.8}}P{r^{0.4}} $ | (8) |
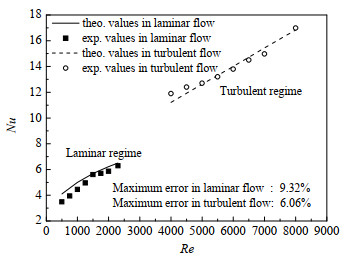
图4为在层流及紊流工况下对去离子水进行对流传热验证。由图可知,2种流动状态下实验值与关联式的吻合度较高,层流及紊流下最大误差分别显示为9.32% 和6.06%,都在可接受的误差范围内,这说明试验系统精度可满足需要。
|
图 4 层流及紊流区Nu数验证(工质水) Fig.4 Validation of Nusselt number in laminar and turbulent flow regions (Deionized water) |
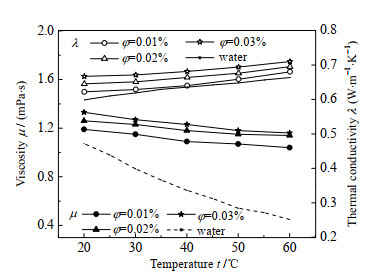
如图5所示为Al2O3-CuO/水混合纳米流体的黏度μ与导热系数λ随温度及体积分数的变化。从图中可以看到,随着体积分数增大,导热系数与黏度均增大;随着温度的升高,导热系数增大而黏度降低,其变化规律与一元纳米流体相似,说明混合纳米流体也具有纳米流体的普遍特性。在温度为20 ℃和体积分数为0.01% 时,与同温度下的去离子水相比,导热系数增幅仅为2.6%;但当温度升高至60 ℃、体积分数增大至0.03%,此时与同温度下的去离子水相比,导热系数增幅至8.4%。
|
图 5 Al2O3-CuO/水纳米流体导热系数和黏度随体积分数和温度的变化 Fig.5 Profiles of thermal conductivity and viscosity of Al2O3-CuO/water nanofluids under different volume fractions and temperatures |
这是因为随着体积分数增大,基液中纳米粒子的数量增多,粒子间相互碰撞的几率增大,使其热交换作用增强,宏观表现为导热系数增大;但纳米流体的稳定性随着粒子数量的增多而减弱,粒子间的布朗运动加速其团聚速度,由于团聚体的尺寸大于单一粒子,因此需要克服更大的流动阻力才能使团聚体在流体内部运动,宏观表现为黏度增大。结合图1 TEM,这是因为小粒径Al2O3粒子能填充进由大粒径CuO粒子形成的缝隙中,形成致密的粒子分布,即更紧凑的固液界面,降低界面热阻。Akhgar等[28]也指出,在高温及大体积分数下,粒子热运动加剧团聚,在纳米粒子间形成了链态现象,形成了一条高热传导的路径,使传热高于基液状态。
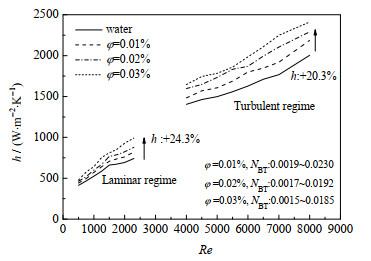
如图6所示为Al2O3-CuO/水混合纳米流体对流传热系数h随雷诺数Re的变化。从图中可以看到,随着体积分数增大,对流传热系数逐渐增大。当体积分数从0.01% 增大到0.03% 时,与去离子水比,对流传热系数在层流与紊流最大增幅分别达24.3% 与20.3%。在层流区,当雷诺数从0增大到2 300时,去离子水与体积分数为0.03% 的Al2O3-CuO/水纳米流体的对流传热系数h分别增大了44.6% 与52.1%;而在紊流区,当雷诺数从4 000增大到8 000时,二者的对流传热系数h分别增大了30% 与31.8%。
|
图 6 对流传热系数随雷诺数的变化 Fig.6 Variation of heat transfer coefficient with Reynold number |
增强作用一方面是由于纳米粒子Al2O3和CuO的导热系数明显大于去离子水。但由图5可知,纳米颗粒对流体导热系数的增强作用(最高仅达8.4%)远小于对管内对流传热系数的增强作用(最高达24.3%)。因为在静置纳米流体中,纳米粒子在流体中受微观力作用做微对流运动,如布朗运动及由温差引起的热泳运动,二者的共同作用使纳米流体宏观表现为导热系数增大。布朗运动和热泳运动的相互作用力的比值NBT可由式(9)计算[29]:
| $ N_{\mathrm{BT}}=\frac{\text { 布朗扩散力 }}{\text { 热泳扩散力 }} \equiv \frac{\left(2 \lambda+\lambda_{\mathrm{up}}\right) k_{\mathrm{B}} \rho t_{\mathrm{f}}^2}{0.78 \pi \mu^2 \delta_{\mathrm{v}} d_{\mathrm{up}} q}$ | (9) |
式中:λnp为纳米粒子的总导热系数,W⋅m−1⋅K−1,kB、δv和dnp分别为玻尔兹曼常数(1.23×10−23J⋅K−1)、纳米层厚度(≈10−9m)、纳米粒子团聚尺寸(≈2×10−8m)。
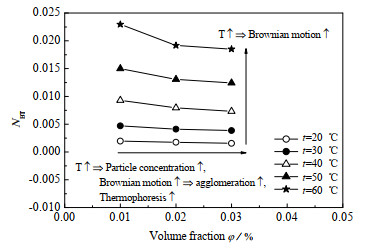
由式(9)量纲分析可知,布朗运动和热泳运动对静置纳米流体的影响量级分别为10−18和10−16。因此,纳米颗粒的热泳作用明显强于布朗运动。如图7所示为NBT随体积分数及温度的变化。从图中可知,NBT随温度的升高而明显增大,随体积分数的增大而减小。这是因为随着流体温度和体积分数升高,流体内部由于粒子数量增多,粒子的迁移运动而引起的布朗运动强度增强,使得流体内部的水分子和固体粒子温度趋于一致的速度加快,如图8(a)所示为静置纳米流体微元团的粒子运动示意图,宏观表现为导热系数增大。
|
图 7 NBT值随体积分数与温度的变化 Fig.7 Variation of NBT with volume fraction and temperature |
|
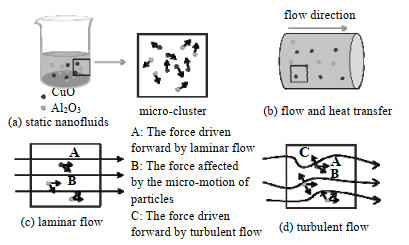
图 8 纳米流体运动受微观力影响示意图 Fig.8 Schematic diagram of micro-motion in nanofluids |
如前所示,在纳米流体管内对流传热过程中,纳米颗粒的迁移运动对对流传热系数的作用大于对静置纳米流体导热系数的增强作用。为了解释这一现象,图8为纳米流体受微观力影响的示意图。如图8(b)所示,纳米流体在管内对流传热过程中,流体携带固体颗粒向前运动,除了受到粒子自身的微运动力作用外,还受到流体整体向前运动的驱动力。在层流传热过程中,流体分子做有序运动,二者共同作用使纳米流体在层流时的传热效果(h=993 W⋅m−2⋅K−1,Re=2 300,φ=0.03%)明显大于去离子水(h=742 W⋅m−2⋅K−1,Re=2 300),如图8(c)所示。而在紊流传热过程中,如图8(d)所示流体分子做无序混乱运动,其传热强度明显大于层流。因此粒子在A、B、C三股力的作用下,紊流时纳米流体(h=2 411 W⋅m−2⋅K−1,Re=8 000,φ=0.03%)的传热强度高于去离子水(h=2 004 W⋅m−2⋅K−1,Re=8 000),但增强作用略低于层流的。
4 结论为了探究粒子迁移对管内对流传热性能的影响,以Al2O3-CuO/水混合纳米流体为工质,分析了体积分数为0.01%~0.03%、温度为20~60 ℃时对静置纳米流体导热系数的影响,并研究在层流Re为0~2 300与紊流Re为4 000~8 000下布朗及热泳运动对对流传热系数的影响规律,得到以下重要结论:
1. Al2O3-CuO/水混合纳米流体的导热系数和黏度随着体积分数增大而增大;随着温度升高、导热系数增大而黏度下降;这与常规纳米流体的变化规律相似。当温度升高至60 ℃、体积分数增大至0.03%,与同温度下的去离子水相比,导热系数增幅至8.4%。
2. 与去离子水对比,在管内对流传热过程中,对流传热系数增幅高达24.3% (层流)与20.3% (紊流),而导热系数最大增幅仅有8.4%,说明导热系数增大仅是纳米流体对流传热系数增大的其中一个原因。
3. 粒子迁移作用使传热效果明显高于去离子水,且对层流强化传热的影响效果大于紊流。从微观角度研究微观力对纳米流体管内对流传热强化可知,流体携带固体颗粒向前运动,受到粒子自身的微运动力及流体整体向前驱动力的共同作用,强化传热效果。
| [1] |
郑钦月, 章学来, 王章飞, 等. 表面活性剂对纳米流体真空制取冰桨的影响[J]. 高校化学工程学报, 2019, 33(2): 435-442. ZHENG Q Y, ZHANG X L, WANG Z F, et al. Effcts of surfactants on vacuum ice-making of nano-fluids[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(2): 435-442. DOI:10.3969/j.issn.1003-9015.2019.02.023 |
| [2] |
RANGA BABU J A, KUMAR K K, SRINIVASA R S. State-of-art review on hybrid nanofluids[J]. Renewable Sustainable Energy Review, 2017, 77(9): 551-565. |
| [3] |
GUPTA M, SINGH V, KUMAR R, et al. A review on thermophysical properties of nanofluids and heat transfer applications[J]. Renewable Sustainable Energy Review, 2017, 74(7): 638-670. |
| [4] |
GUPTA M, SINGH V, KUMAR S, et al. Up to date review on the synthesis and thermophysical properties of hybrid nanofluids[J]. Journal of Cleaner Production, 2018, 190: 169-192. DOI:10.1016/j.jclepro.2018.04.146 |
| [5] |
TURCU R, DARABONT A L, NAN A, et al. New polypyrrole-multiwall carbon nanotubes hybrid materials[J]. Journal of Optoelectronics and Advanced Materials, 2006, 8(2): 643-647. |
| [6] |
翟玉玲. 纳米工质传热过程强化[M]. 北京: 冶金工业出版社, 2021. ZHAI Y L. Nanofluids enhancement in heat transfer process[M]. Beijing: Metallurgical Industry Press, 2021. |
| [7] |
XUAN Z H, ZHAI Y L, MA M Y, et al. Thermo-economic performance and sensitivity analysis of ternary hybrid nanofluids[J]. Journal of Molecular Liquids, 2021, 323: 114889. DOI:10.1016/j.molliq.2020.114889 |
| [8] |
SURESH S, VENKITARAJ K P, HAMEED M S, et al. Turbulent heat transfer and pressure drop characteristics of dilute water based Al2O3-Cu hybrid nanofluids[J]. Journal of Nanoscience and Nanotechnology, 2014, 14(3): 2563-2572. DOI:10.1166/jnn.2014.8467 |
| [9] |
KUMAR D D, ARASU A V. A comprehensive review of preparation, characterization, properties and stability of hybrid nanofluids[J]. Renewable Sustainable Energy Review, 2018, 81(2): 1669-1689. |
| [10] |
HAMID K A, AZMI W H, NABIL M F, et al. Experimental investigation of thermal conductivity and dynamic viscosity on nanoparticle mixture ratios of TiO2-SiO2 nanofluids[J]. International Journal of Heat and Mass Transfer, 2018, 116: 1143-1152. DOI:10.1016/j.ijheatmasstransfer.2017.09.087 |
| [11] |
YU F, CHEN Y Y, LIANG X B, et al. Dispersion stability of thermal nanofluids[J]. Progress in Natural Science- Materials International, 2017, 27(5): 531-542. DOI:10.1016/j.pnsc.2017.08.010 |
| [12] |
ESFE M H, ESFANDEH S, AMIRI M K, et al. A novel applicable experimental study on the thermal behavior of SWCNTs(60%)-MgO(40%)/EG hybrid nanofluid by focusing on the thermal conductivity[J]. Powder Technology, 2018, 342: 998-1007. |
| [13] |
APARNA Z, MICHAEL M, PABI S K, et al. Thermal conductivity of aqueous Al2O3/Ag hybrid nanofluid at different temperatures and volume concentrations: An experimental investigation and development of new correlation function[J]. Powder Technology, 2019, 343: 714-722. DOI:10.1016/j.powtec.2018.11.096 |
| [14] |
GOYAL M, SHARMA K. Investigation on forced convective heat transfer characteristics of carbon nanomaterial based nanofluids[J]. Materials Today:Proceedings, 2021, 37(8): 3019-3023. |
| [15] |
DEMIRKIR C, ERTURK H. Convective heat transfer and pressure drop characteristics of graphene-water nanofluids in transitional flow[J]. International Journal of Heat and Mass Transfer, 2021, 121: 105092. |
| [16] |
SALEH B, SUNDAR L S. Entropy generation and exergy efficiency analysis of ethylene glycol-water based nanodiamond + Fe3O4 hybrid nanofluids in a circular tube[J]. Powder Technology, 2021, 380: 430-442. DOI:10.1016/j.powtec.2020.12.006 |
| [17] |
HO C J, CHENG C Y, YANG T F, et al. Experimental study on cooling performance of nanofluid flow in a horizontal circular tube[J]. International Journal of Heat and Mass Transfer, 2021, 169: 120961. DOI:10.1016/j.ijheatmasstransfer.2021.120961 |
| [18] |
ALI H M. In tube convection heat transfer enhancement: SiO2 aqua based nanofluids[J]. Journal of Molecular Liquids, 2020, 308: 113031. DOI:10.1016/j.molliq.2020.113031 |
| [19] |
CHOI T J, PARK M S, KIM S H, et al. Experimental study on the effect of nanoparticle migration on the convective heat transfer coefficient of EG/water-based Al2O3 nanofluids[J]. International Journal of Heat and Mass Transfer, 2021, 169: 120903. DOI:10.1016/j.ijheatmasstransfer.2021.120903 |
| [20] |
MEHRALI M, SADEGHINEZHAD E, ROSEN M A, et al. Effect of specific surface area on convective heat transfer of graphene nanoplatelet aqueous nanofluids[J]. Experimental Thermal and Fluid Sciences, 2015, 68: 100-108. DOI:10.1016/j.expthermflusci.2015.03.012 |
| [21] |
BAHIRAEI M, HOSSEINALIPOUR S M. Particle migration in nanofluids considering thermophoresis and its effect on convective heat transfer[J]. Thermochimica Acta, 2013, 574: 47-54. DOI:10.1016/j.tca.2013.09.010 |
| [22] |
ALI H M. Hybrid nanofluids for convection heat transfer[M]. Pittsburgh, USA: Academic Press, 2020.
|
| [23] |
MA M Y, ZHAI Y L, YAO P T, et al. Synergistic mechanism of thermal conductivity enhancement and economic analysis of hybrid nanofluids[J]. Powder Technology, 2020, 373: 702-715. DOI:10.1016/j.powtec.2020.07.020 |
| [24] |
DAS P K. A review based on the effect and mechanism of thermal conductivity of normal nanofluids and hybrid nanofluids[J]. Journal of Molecular Liquids, 2017, 240: 420-446. DOI:10.1016/j.molliq.2017.05.071 |
| [25] |
杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006. YANG S M, TAO W Q. Heat transfe[M]. Beijing: High Education Press, 2006. |
| [26] |
AZMI W H, SHARMA K V, MAMAT R, et al. The enhancement of effective thermal conductivity and effective dynamic viscosity of nanofluids - A review[J]. Renewable and Sustainable Energy Reviews, 2016, 53: 1046-1058. DOI:10.1016/j.rser.2015.09.081 |
| [27] |
SINGH S K, SARKAR J. Energy, exergy and economic assessments of shell and tube condenser using hybrid nanofluid as coolant[J]. International Journal of Heat and Mass Transfer, 2018, 98: 41-48. |
| [28] |
AKHGAR A, TOGHRAIE D. An experimental study on the stability and thermal conductivity of water-ethylene glycol/TiO2-MWCNTs hybrid nanofluid: Developing a new correlation[J]. Powder Technology, 2018, 338: 806-818. DOI:10.1016/j.powtec.2018.07.086 |
| [29] |
BUONGIORNO J. Convective transport in nanofluids[J]. Journal of Heat Transfer, 2006, 128(3): 240-250. DOI:10.1115/1.2150834 |




