脂肪酸酯类是生物柴油的主要成分,因黏度较大,通常添加一定比例的醇类物质对流动特性进行改进。因此,醇类+脂肪酸酯类混合物的黏度信息对于燃油的流动特性具有重要的研究价值。由于混合体系的黏度实验测量成本较高,技术人员更加青睐于利用可靠的理论模型对黏度进行估算[1]。其中,McAllister基于Eyring绝对反应速率理论所提出的两参数方程[2],通常简称为“McAllister三体模型”,被认为是二元体系运动黏度的最佳关联模型。由于原始McAllister三体模型的预测性能较差,Asfour等[3]曾基于碳原子数和纯物质的黏度,试图拓展模型的应用范围,但其研究忽略了温度对模型参数的影响,导致修正模型的计算精度大幅度降低。鉴此,本研究通过搜集和整理文献中二元混合物的密度与黏度数据,研究McAllister三体模型对于黏度计算的适用性。围绕基于温度的交互作用参数计算方法展开研究,提出一种计算模型参数的新方法,以拓展McAllister三体模型所适用的温度范围。
2 原始McAllister三体模型简介在绝对反应速率理论中,Eyring[4]假设运动是一个平面(层)的单分子获得活化能,滑过势垒到达同一平面上的另一个平衡位置。在运动方向上,这些平衡位置之间的平均距离取λ,相邻分子层间的垂直距离取λ1,同一方向上相邻分子间的平均距离取λ2,在垂直运动方向的平面上,分子到分子的距离取λ3。由此得到黏度的模型如下:
| $ \eta = \frac{{{\lambda _1}h}}{{{\lambda ^2}{\lambda _2}{\lambda _3}}}{\text{ex}}{{\text{p}}_{}}{\text{(}}\Delta {G^ * }{\text{/}}kT{\text{)}} $ | (1) |
式中:η为黏度,Pa·s;h为普朗克常数,J·s;ΔG*为活化自由能,kJ·mol−1;k为玻尔兹曼常数,J·K;T为热力学温度,K。
Eyring假设λ1近似等于λ,式(1)变为
| $ \eta = \frac{{h {N_{\text{A}}}}}{V}{\text{ex}}{{\text{p}}_{}}{\text{(}}\Delta {G^ * }{\text{/}}kT{\text{)}} 或 \nu = \frac{{h {N_{\text{A}}}}}{M}{\text{ex}}{{\text{p}}_{}}{\text{(}}\Delta {G^ * }{\text{/}}kT{\text{)}} $ | (2) |
式中:V为摩尔体积,m3·mol−1;NA为阿伏加德罗常数,mol−1;ν为运动黏度,mm2·s−1;M为摩尔质量,kg·mol−1。
在研究二元体系时,McAllister认为分子的空间运动状态可分为2大类:第1类包括2个A分子和1个B分子(包括ABA,BAA,AAB排列组合);第2类包括1个A分子和2个B分子(包括BAB,ABB,BBA排列组合),并分别用ν12和ν21对第1类和第2类运动状态下分子间的相互作用关系进行了定义。在研究二元混合物时,McAllister对于活化自由能的定义如下:
| $ \Delta {G^*} = x_1^3\Delta G_1^* + x_1^2{x_2}\Delta G_{121}^* + 2x_1^2{x_2}\Delta G_{112}^* + {x_1}x_2^2\Delta G_{212}^* + 2{x_1}x_2^2\Delta G_{122}^* + x_2^3\Delta G_2^* $ | (3) |
| $ \Delta G_{121}^* = \Delta G_{112}^* \equiv \Delta G_{12}^* $ | (4) |
| $ \Delta G_{212}^* = \Delta G_{122}^* \equiv \Delta G_{21}^* $ | (5) |
联合式(3)~(5)可得
| $ \Delta {G^*} = x_1^3\Delta G_1^* + 3x_1^2{x_2}\Delta G_{12}^* + 3{x_1}x_2^2\Delta G_{21}^* + x_2^3\Delta G_2^* $ | (6) |
式中:x1和x2分别为纯物质1和纯物质2的摩尔分数;ΔG1*为含A分子的活化自由能,kJ·mol−1;ΔG2*为含B分子的活化自由能,kJ·mol−1;ΔG12*为含1个A分子2个B分子的活化自由能,kJ·mol−1;ΔG21*为含2个A分子1个B分子的活化自由能,kJ·mol−1。
McAllister定义各种相互作用类型所对应的摩尔质量如下:
| $ \begin{gathered} {M_{{\text{avg}}}} = {x_1}{M_1} + {x_2}{M_2} \hfill \\ {M_{12}} = (2{M_1} + {M_2})/3 \hfill \\ {M_{21}} = ({M_1} + 2{M_2})/3 \hfill \\ \end{gathered} $ | (7) |
式中:Mavg为二元混合物的平均摩尔质量,kg·mol−1;M1和M2分别为纯物质1和纯物质2的摩尔质量,kg·mol−1;M12为含1个A分子和2个B分子的等效摩尔质量,kg·mol−1;M21为含2个A分子和1个B分子的等效摩尔质量,kg·mol−1。
McAllister基于等效摩尔质量和活化自由能,推导出混合物体系黏度与纯物质黏度、摩尔质量及体系组分间的函数关系,通常称为“McAllister三体模型”,具体推导过程参见文献[2]。数学表达式如下:
| $ \begin{gathered} \ln {\nu _{m} } = x_1^3\ln {\nu _1} + 3x_1^2{x_2}\ln {\nu _{12}} + 3{x_1}x_2^2\ln {\nu _{21}} + x_2^3\ln {\nu _2} - \ln \left( {{x_1} + {x_2}\left( {{{{M_2}} \mathord{\left/ {\vphantom {{{M_2}} {{M_1}}}} \right. } {{M_1}}}} \right)} \right) + \\ 3x_1^2{x_2}\ln \left( {{{\left( {2 + \left( {{{{M_2}} \mathord{\left/ {\vphantom {{{M_2}} {{M_1}}}} \right. } {{M_1}}}} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {2 + \left( {{{{M_2}} \mathord{\left/ {\vphantom {{{M_2}} {{M_1}}}} \right. } {{M_1}}}} \right)} \right)} 3}} \right. } 3}} \right) + 3{x_1}x_2^2\ln \left( {{{\left( {1 + 2\left( {{{{M_2}} \mathord{\left/ {\vphantom {{{M_2}} {{M_1}}}} \right. } {{M_1}}}} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {1 + 2\left( {{{{M_2}} \mathord{\left/ {\vphantom {{{M_2}} {{M_1}}}} \right. } {{M_1}}}} \right)} \right)} 3}} \right. } 3}} \right) + x_2^3\ln \left( {{{{M_2}} \mathord{\left/ {\vphantom {{{M_2}} {{M_1}}}} \right. } {{M_1}}}} \right) \\ \end{gathered} $ | (8) |
式中:νm为混合体系的运动黏度,mm2·s−1;ν1和ν2分别为纯物质1和纯物质2的运动黏度,mm2·s−1;ν12为含1个A分子和2个B分子的交互作用参数,mm2·s−1,ν21为含2个A分子和1个B分子的交互作用参数,mm2·s−1。
3 新型McAllister三体模型的建立本研究主要以醇类+脂肪酸酯类二元混合物为研究对象[5-12],通过文献调研获得29种二元体系的黏度和密度实验值,密度合计2 302个实验点,黏度合计2 302个实验点,研究的温度范围为283.15~343.15 K,压力工况均为常压,表 1列出了所有物质体系的基本信息。由于McAllister三体模型是针对运动黏度ν(mm2·s−1)的理论研究,而在流体热物性领域中,通常以动力黏度η(Pa·s)作为对比基准。因此,要建立较为完善的动力黏度计算模型,首先要得到准确的密度ρ(kg·m−3)数据。
|
|
表 1 二元混合体系的基本信息 Table 1 Basic information of the binary hybrid system |
为了方便快速获得所需的混合物密度数据,利用热力学温度和纯物质的摩尔分数对混合物的密度进行关联,函数式如下:
| $ {\rho _m} = \sum\limits_{\begin{smallmatrix} i\text{ }=\text{ }0 \\ j=0 \end{smallmatrix}}^{n=4}{\left( {{A}_{i}}\text{ }+\text{ }{{B}_{i}}T \right)x_{1}^{j}} $ | (9) |
式中:ρm为混合体系的密度,kg·m−3;Ai、Bi为方程待定系数,通过最小二乘法得到;i表示x1系数中参数(A,B)的序列号;j表示x1的幂。
偏差统计表明,利用方程(9)计算得到的混合物密度ρm,总体平均相对偏差(overall-average-relative-deviation,ARD)为0.01%,最大相对偏差(maximum-relative-deviation,MRD)为0.11%,基本满足密度计算的精度要求。由此认为,所建立的密度计算模型是可靠的,可用于本研究中混合体系运动黏度与动力黏度的精确转换。基于所建立的密度方程,验证McAllister三体模型对本研究二元体系黏度计算的适用性。
本研究搜集得到29种不同配比的二元体系在不同温度的黏度与密度数据。将文献中其他数据通过拟合得到McAllister三体模型的交互作用参数(ν12与ν21)。结果表明,动力黏度η计算的ARD小于0.80%,MRD在7.50% 以内。由此可见,McAllister三体模型可对本研究二元体系的黏度数值进行较好地复现。
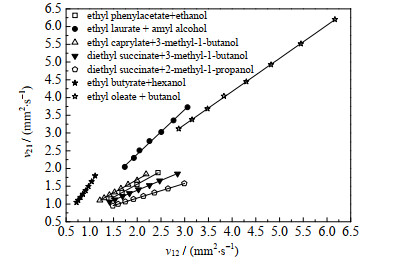
在此基础上,本研究期望对原始模型进行优化,提出一种基于温度的交互作用参数计算方法,以拓展McAllister三体模型适用的温度范围。基于交互作用参数的拟合结果,研究发现,两个交互作用参数ν12与ν21间呈现较好的线性关系,相关性系数(relative coefficient,R2)在0.991 97~0.999 97,残差平方和(residual sum of squares,RSS)在2.36×10−6~0.036。图 1分别给出了苯乙酸乙酯+乙醇、十二酸乙酯+戊醇、辛酸乙酯+3-甲基-1-丁醇、丁二酸二乙酯+3-甲基-1-丁醇、丁二酸二乙酯+2-甲基-1-丙醇、丁酸乙酯+己醇、油酸乙酯+丁醇等二元体系,在所研究的温度范围内,两个交互作用参数之间的变化规律。由图 1可知,ν21与ν12具有较强的正相关性。因此,作者认为本研究所有体系的两个McAllister模型交互作用参数间的关系,可用如下通用化的函数式进行表示:
| $ {{\text{v}}_{21}} = a + b{v_{12}} $ | (10) |
|
图 1 交互作用参数ν12与ν21之间的变化规律 Fig.1 Relationship between interaction parameters ν12 and ν21 |
式中:a和b为方程系数,可通过最小二乘法得到,列于表 2;表 2中的p1、p2为方程(13)的待定系数。
|
|
表 2 交互作用参数的方程系数 Table 2 Equation coefficients of interaction parameters |
利用ν12与ν21的函数关系,即可对原始McAllister三体模型进行优化。在对二元混合物黏度进行测量过程中,由于不同物质的饱和蒸气压差异较大,在进行高温测量时,混合物的组分极易因挥发而发生变化。因此,通常情况下测量混合物黏度的温度点较低。但是,在工业生产中通常需要较高温度的黏度数据,故作者倾向于应用理论方法来预测较高温度范围的二元体系黏度。而对于方程(10)中ν12的求解,考虑到在常压下,273.15 K < T < 373.15 K温度范围内,纯水的运动黏度νw通常是易于得到的。因此,本研究期望通过对ν12与νw、T之间的关系进行研究,从而提出计算ν12的方法。在本研究中,首先对热力学温度T和交互作用参数ν12进行无量纲化:
| $ {T_{\text{r}}} = T/{T_{\min }} $ | (11) |
| $ {\nu _{\text{r}}}{\text{ = }}{\nu _{12}}/{\nu _{\text{w}}} $ | (12) |
式中:Tr为T的无量纲参数;νr为ν12的无量纲参数;Tmin为实验测量的最低温度点,K;νw为纯水的运动黏度,mm2·s−1(源于REFPROP 9.1)。
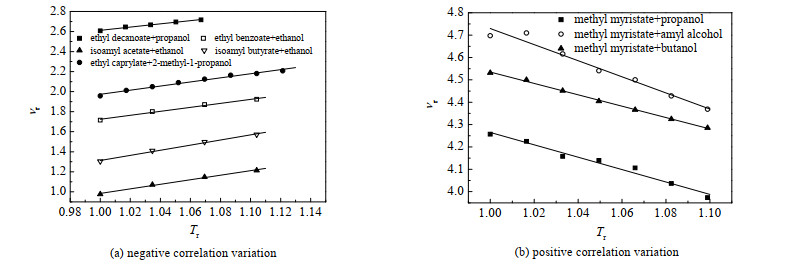
图 2展示了几种二元体系的νr随Tr的变化规律,包括肉豆蔻酸甲酯+丙醇、肉豆蔻酸甲酯+戊醇、肉豆蔻酸甲酯+丁醇、癸酸乙酯+丙醇、辛酸乙酯+2-甲基-1-丙醇、乙酸异戊酯+乙醇、丁酸异戊酯+乙醇、苯甲酸乙酯+乙醇。由图 2可以发现,νr与Tr间呈现较强的线性相关性。通过研究分析,作者认为νr与Tr之间满足如下关系:
| $ {\nu _{\text{r}}}{\text{ = }}{p_1} + {p_2}{T_{\text{r}}} $ | (13) |
|
图 2 νr随Tr的变化规律 Fig.2 Profiles of νr as a function of Tr |
式中:p1、p2为方程待定系数,通过最小二乘法得到。
利用式(13)的函数关系,McAllister三体模型可用于推算较宽温度范围的二元混合物黏度值,根据参考物质的运动黏度νw,估计模型适用的温度范围为273.15 K < T < 373.15 K。由以上分析可知,对于所研究的二元混合物,在已知热力学温度T,参数p1、p2,纯水的运动黏度νw,参数a、b的前提下,可利用方程(10)~(13)对交互作用参数(ν12和ν21)进行求解。再结合纯物质的运动黏度ν1和ν2、纯物质的摩尔分数x1和x2、纯物质的摩尔质量M1和M2,通过方程(8)计算得到二元混合物的运动黏度值νm。最后根据密度计算方程(9)即可对混合物的动力黏度进行求解。需要说明的是,在上述建立模型的过程中,油酸乙酯+丁醇(333.15~343.15 K)、癸酸乙酯+丙醇/丁醇/戊醇(283.15~293.15 K)的数据并未用于建模。
4 综合性评价与讨论将原始McAllister三体模型和新模型的动力黏度计算结果与实验值进行比较。同样采用ARD与MRD两项指标进行评价。表 3列出了本研究29种二元体系黏度计算的相对偏差结果。表 3中的ARDo、ARDn分别为原始模型和新模型总体平均相对偏差,MRDo、MRDn分别为原始模型和新模型最大相对偏差。由表 3可知,对于大多数二元体系,新模型和原始模型的相对偏差基本一致。原始模型与新模型的最佳ARD分别为0.71% 和0.75%,最佳MRD分别为7.35% 和7.41%,新模型的偏差虽然仅略高于原始模型,但是新模型的计算方法适用的温度范围更大,多数二元体系的ARD均在1% 以内,这说明新模型具有较好的计算精度。
|
|
表 3 新模型与原始模型计算结果的相对偏差 Table 3 Relative deviations of the calculation results of the new and original models |
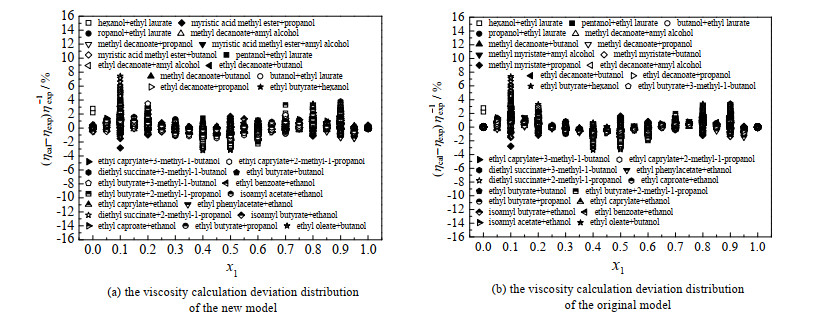
图 3分别给出了新模型与原始模型计算值的相对偏差分布。其中,ηcal和ηexp分别为黏度的计算值与实验值。从图中可以看出,新模型和原始模型的偏差分布情况基本一致,所有二元混合体系的计算结果都不存在系统性偏差;除了丁二酸二乙酯+2-甲基-1-丙醇/3-甲基-1-丁醇等二元体系,对于原始模型和新模型,大多数偏差点落在±3%以内。通过研究发现,“丁二酸二乙酯+2-甲基-1-丙醇”与“丁二酸二乙酯+3-甲基-1-丁醇”之所以存在较大的计算偏差,其主要原因是“丁二酸二乙酯、2-甲基-1-丙醇、3-甲基-1-丁醇”等3种物质结构上的复杂性与不对称性,导致在混合溶液中酯类分子与醇类分子间产生了协同效应,即在整个组分范围内,二元混合溶液的黏度变化呈现出凹陷的抛物线趋势,不符合常规的线性变化规律。
|
图 3 黏度计算偏差分布 Fig.3 Deviation distribution of viscosity calculation |
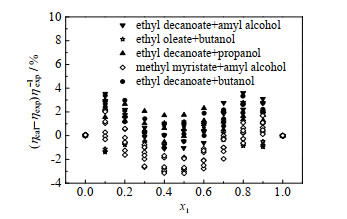
为验证新模型能预测更宽温度范围的二元体系黏度,将未参与建模的二元体系的数据点代入新模型进行计算,黏度、密度实验点个数分别为209个,包括油酸乙酯+丁醇(333.15~343.15 K)、癸酸乙酯+丙醇/丁醇/戊醇(283.15~293.15 K)、肉豆蔻酸甲酯+戊醇(293.15~323.15 K)[13],并将其预测结果和文献数据进行了比较。5种二元体系的平均相对偏差列于表 4,从图中可看出,最佳ARD和MRD分别为1.12% 和3.88%,图 4给出了基于新模型黏度计算结果的相对偏差分布。从图中可以看出,新模型的计算精度仍然较高。由此说明,本研究所建立的预测方法,可用于估算273.15 K < T < 373.15 K范围的二元混合物黏度。
|
|
表 4 醇类+脂肪酸酯类二元体系的新模型计算结果的相对偏差 Table 4 Relative deviations of the new model for binary system of alcohols + fatty acids esters |
|
图 4 验证新模型的黏度计算偏差分布 Fig.4 Verification of calculation deviation distribution of the new model |
综上所述,对于本研究提出的一种交互作用参数相互推导计算的新方法,作者用未参与建模的实验数据进行验证,证明了McAllister三体模型可用于预测较宽温度范围条件下的二元体系黏度值。本研究对McAllister三体模型的改进,为模型适用的温度范围提供了一种新思路。偏差分析对比结果表明,新模型仍具有较高的计算精度,可用于二元混合物的黏度推算,满足工程实际的需求。
6 同类模型间比较Jouyban-Acree模型和非随机双液模型(nonrandom two-liquid,NRTL)被广泛用于二元体系的黏度计算。为了进一步验证新模型的可行性与优势,选择有温度影响效应的Jouyban-Acree模型、NRTL模型,与本研究改进的三体模型的计算偏差进行比较。Jouyban-Acree模型如下所示[14]:
| $ \ln {\eta _{\text{m}}} = {x_1}\ln {\eta _1} + {x_2}\ln {\eta _2} + {A_0}[{x_1}{x_2}/T] + {A_1}[{x_1}{x_2}({x_1} - {x_2})/T] + {A_2}[{x_1}{x_2}{({x_1} - {x_2})^2}/T] $ | (14) |
式中:ηm为混合体系黏度,Pa·s;η1和η2分别为纯物质1和纯物质2的黏度,Pa·s;A0、A1、A2为可调交互参数,通过最小二乘法得到,列于表 5;表 5中
|
|
表 5 Jouyban-Acree模型和NRTL模型的参数表 Table 5 Parameters of the Jouyban-Acree and NRTL models |
NRTL模型如下[15]:
| $ \begin{gathered} {\ln_{}}{\eta _{\text{m}}} = {x_1}\ln {\eta _1} + {x_2}\ln {\eta _2} + {x_1}{x_2}((({\Delta _{}}g_{21}^{(0)} + {\Delta _{}}g_{21}^{(1)}/T)/(RT)){\text{e}^{ - 0.1({\Delta _{}}g_{21}^{(0)} + {\Delta _{}}g_{21}^{(1)}/T)/(RT)}}/({x_1} + {x_2}{\text{e}^{ - 0.1({\Delta _{}}g_{21}^{(0)} + {\Delta _{}}g_{21}^{(1)}/T)/(RT)}}) + \\ (({\Delta _{}}g_{12}^{(0)} + {\Delta _{}}g_{12}^{(1)}/T)/(RT)){\text{e}^{ - 0.1({\Delta _{}}g_{12}^{(0)} + {\Delta _{}}g_{12}^{(1)}/T)/(RT)}}/({x_2} + {x_1}{\text{e}^{ - 0.1({\Delta _{}}g_{12}^{(0)} + {\Delta _{}}g_{12}^{(1)}/T)/(RT)}})) \\ \end{gathered} $ | (15) |
式中:R为摩尔气体常数,8.314 J·(mol·K)−1;
从所研究的物质中,选择温度范围相对较宽的二元体系,包括油酸乙酯+丙醇(293.15~343.15 K)、癸酸乙酯+戊醇(283.15~318.15 K)、丁二酸二乙酯+3-甲基-1-丁醇(288.15~323.15 K)、辛酸乙酯+2-甲基-1-丙醇(288.15~323.15 K)、癸酸甲酯+1-丙醇(298.15~333.15 K)、丁酸乙酯+1-己醇(288.15~323.15 K)、肉豆蔻酸甲酯+1-丁醇(303.15~333.15 K),进行模型对比工作。表 6给出了新McAllister三体模型与Jouyban-Acree模型、NRTL模型的对比结果,最佳总体平均相对偏差分别为0.93%,1.68%,1.83%,由此可见,McAllister三体模型比同类模型计算精度高。
|
|
表 6 McAllister三体模型与Jouyban-Acree模型和NRTL模型的偏差对比 Table 6 Comparison of McAllister three-body model with Jouyban-Acree and NRTL models |
本研究主要以脂肪酸酯类、醇类所组成的二元混合物为研究对象,通过对McAllister三体模型交互作用参数ν12与ν21及纯水的运动黏度νw、热力学温度T间定量关系的深入研究,提出了一种可用于预测较宽温度范围的二元体系黏度的新计算方法。用新模型对二元混合物黏度进行推算的总体平均相对偏差为0.75%。作者对新模型进行了验证,并将其与Jouyban-Acree模型、NRTL模型进行了比较,结果表明改进的McAllister三体模型的计算精度更高。由此认为,新模型适用于推算273.15 K < T < 373.15 K温度范围的醇类+脂肪酸酯类二元体系黏度,且计算精度较高,使McAllister三体模型的适用性得到改善。
| [1] |
MEHROTRA A K, MONNERY W D, SVRCEK W Y. A review of practical calculation methods for the viscosity of liquid hydrocarbons and their mixtures[J]. Fluid Phase Equilibria, 1996, 117(1/2): 344-355. |
| [2] |
MCALLISTER R A. The viscosity of liquid mixtures[J]. AIChE Journal, 1960, 6(3): 427-431. DOI:10.1002/aic.690060316 |
| [3] |
NHAESI A H, ASFOUR A F A. Prediction of the viscosity of multi-component liquid mixtures: A generalized McAllister three-body interaction model[J]. Chemical Engineering Science, 2000, 55(15): 2861-2873. DOI:10.1016/S0009-2509(99)00541-2 |
| [4] |
EYRING H. Viscosity, plasticity, and diffusion as examples of absolute reaction rates[J]. Journal of Chemical Physics, 1936, 4(4): 283-291. DOI:10.1063/1.1749836 |
| [5] |
AISSA M A, RADOVIC I R, SIMIC Z V, et al. Thermodynamic and transport properties of ternary mixture (ethyl oleate + n-hexadecane+1-butanol) and its binary constituents (ethyl oleate+1-butanol and ethyl oleate + n-hexadecane) at different temperatures and atmospheric pressure[J]. Journal of Molecular Liquids, 2020, 317(11): 1-19. |
| [6] |
SHEN Y W, TU C H. Densities and viscosities of binary mixtures of isoamyl acetate, ethyl caproate, ethyl benzoate, isoamyl butyrate, ethyl phenylacetate, and ethyl caprylate with ethanol at T = (288.15, 298.15, 308.15, and 318.15) K[J]. Journal of Chemical and Engineering Data, 2006, 51(2): 496-503. DOI:10.1021/je050389b |
| [7] |
BAJIC D M, ZIVKOVIC E M, SERBANOVIC S S, et al. Volumetric and viscometric study of binary systems of ethyl butyrate with alcohols[J]. Journal of Chemical and Engineering Data, 2014, 59(11): 3677-3690. DOI:10.1021/je5005752 |
| [8] |
MAJSTOROVIC D M, ZIVKOVIC E M, MATIJA L R, et al. Volumetric, viscometric, spectral studies and viscosity modelling of binary mixtures of esters and alcohols (diethyl succinate, or ethyl octanoate + isobutanol, or isopentanol) at varying temperatures[J]. Journal of Chemical Thermodynamics, 2017, 104(1): 169-188. |
| [9] |
WANG X J, WANG X P, WANG D B. Volumetric and viscometric properties of ethyl caprate + 1-propanol, + 1-butanol, and + 1-pentanol from 283.15 K to 318.15 K[J]. Journal of Molecular Liquids, 2017, 225(1): 311-319. |
| [10] |
YANG F X, WANG X P, TAN H Z, et al. Experimental investigations on the thermophysical properties of methyl myristate in alcoholic solutions[J]. Fuel, 2018, 215(3): 187-195. |
| [11] |
DU W B, WANG X P. Density and viscosity for binary mixtures of methyl decanoate with 1-propanol, 1-butanol, and 1-pentanol[J]. Journal of Molecular Liquids, 2019, 294(11): 1-13. |
| [12] |
LI D, GUO M, WU Q, et al. Investigations on the thermophysical properties of the binary mixtures of ethyl laurate with four n-alkanols[J]. Journal of Solution Chemistry, 2020, 49(9/10): 1-13. |
| [13] |
LI D, ZHENG Y J, WANG J Y, et al. Volumetric properties and viscosity for the ternary system of (1-pentanol + ethylcyclohexane + methyl myristate) and corresponding binary systems at T = 293.15-323.15 K[J]. The Journal of Chemical Thermodynamics, 2022, 165: 1-8. |
| [14] |
JOUYBAN A, KHOUBNASABJAFARI M, VAEZ-GHARAMALEKI Z, et al. Calculation of the viscosity of binary liquids at various temperatures using Jouyban-Acree model[J]. Chemical and Pharmaceutical Bulletin, 2005, 53(5): 519-523. |
| [15] |
RENON H, PRAUSNITZJ M. Local compositions in thermodynamic excess functions for liquid mixtures[J]. AIChE Journal, 1968, 14(1): 135-144. |




